Санкт-Петербургский университет информационных технологий, механики и оптики
Кафедра прикладной экономики и маркетинга
Практическая работа №2
«Исследование корреляционной связи»
Выполнил: Рочев Максим
Группа 2070
Проверил:
Санкт-Петербург
2010
Исходные данные:
Данные о затратах на рекламу и количеству туристов, воспользовавшихся услугами турфирм.
| № турфирм |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| Затраты на рекламу, у.е.д. |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
| Число туристов, чел. |
820 |
950 |
970 |
900 |
1200 |
1150 |
1000 |
1200 |
1100 |
1000 |
Цель работы: построение однофакторной корреляционной модели и ее интерпретация.
1)
Выявление связи между признаками
– визуализация связи (построение и визуальный анализ корреляционного поля)
Корреляционное поле
представляет собой совокупность точек 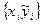 . Если в расположении точек наблюдается определенная зависимость, то связь между признаками существует. . Если в расположении точек наблюдается определенная зависимость, то связь между признаками существует.
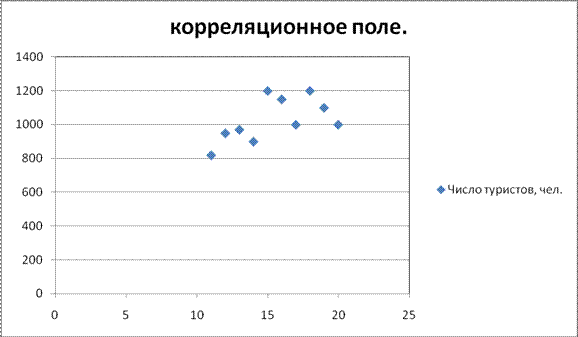
При анализе корреляционного поля в расположении точек наблюдается определенная зависимость: изменение затрат на рекламу у.д.е. (факторного признака) влечет некоторое изменение числа туристов (результативного признака), следовательно, связь между признаками существует.
2)
Описание выявленной связи
в табличной форме
–
статистические единицы группируются по значению факторного признака (в порядке его возрастания или убывания):
| № п/п |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
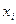 |
Затраты на рекламу, у.е.д. |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
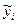 |
Число туристов, чел. |
820 |
950 |
970 |
900 |
1200 |
1150 |
1000 |
1200 |
1100 |
1000 |
в графической форме
– в виде линии эмпирической регрессии
– ломаной линии, соединяющей на корреляционном поле точки, абсциссами которых являются значения факторного признака (индивидуальные или групповые), а ординатами – средние значения результативного признака:
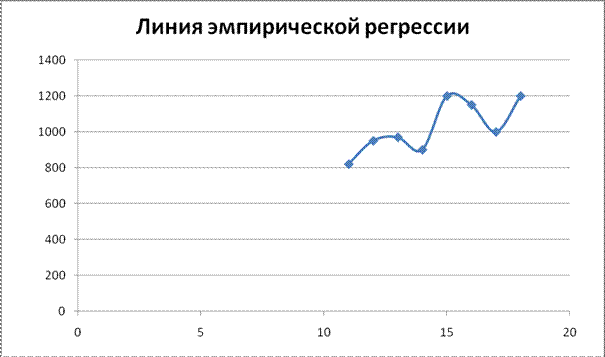
Линия эмпирической регрессии отражает основную тенденцию рассматриваемой зависимости. По своему виду она приближается к прямой линии, можно предположить наличие прямолинейной связи между признаками.
в аналитической форме
:
Аналитически выявленная связь описывается корреляционной моделью. Для построения используются различные математические функции. Подбор функции осуществляется на основе анализа эмпирической линии регрессии.
В данном случае используем полином первой степени, так как эмпирическая линия регрессии стремиться к прямой:
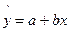
Для нахождения численного значения параметров обращаемся к методу «наименьших квадратов» (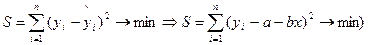 и системе нормальных уравнений: и системе нормальных уравнений:
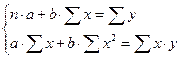
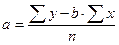
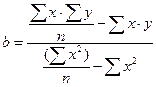
Расчетная таблица для определения параметров корреляционной модели вида
| № |
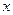 |
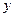 |
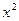 |
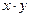 |
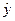 |
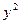 |
| 1 |
11 |
820 |
121 |
9020 |
917,85 |
672400 |
| 2 |
12 |
950 |
144 |
11400 |
942,55 |
902500 |
| 3 |
13 |
970 |
169 |
12610 |
967,25 |
940900 |
| 4 |
14 |
900 |
196 |
12600 |
991,95 |
810000 |
| 5 |
15 |
1200 |
225 |
18000 |
1016,65 |
1440000 |
| 6 |
16 |
1150 |
256 |
18400 |
1041,35 |
1322500 |
| 7 |
17 |
1000 |
289 |
17000 |
1066,05 |
1000000 |
| 8 |
18 |
1200 |
324 |
21600 |
1090,75 |
1440000 |
| 9 |
19 |
1100 |
361 |
20900 |
1115,45 |
1210000 |
| 10 |
20 |
1000 |
400 |
20000 |
1140,15 |
1000000 |
 |
155 |
10290 |
2485 |
161530 |
10290 |
10738300 |
На основе вычислений получаем:
b=24,7
a=646,15
следовательно, 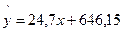 – корреляционная модель
.
– корреляционная модель
.
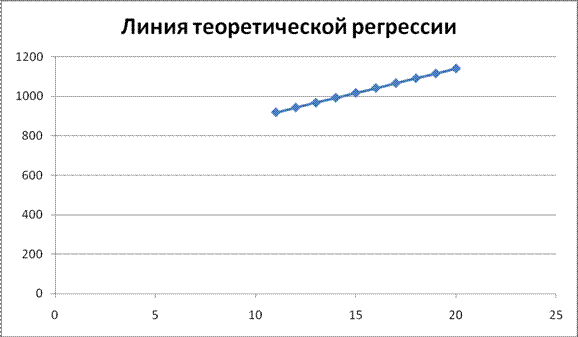
Построенная корреляционная модель представляется графически в виде линии теоретической регрессии – ломаной линии, соединяющей точки с координатами 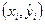 . .
Реклама

3)
Изменение тесноты связи
Показывает меру влияния факторного признака на общую вариацию результативного.
Показателем тесноты связи для линейных моделей является линейный коэффициент корреляции 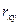 , рассчитываемый по формуле:
, рассчитываемый по формуле:
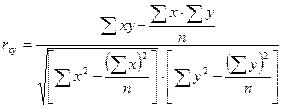
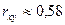
По численному значению линейного коэффициента корреляции связь классифицируется по степени ее тесноты с использованием шкалы Чеддока:
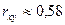 - заметная - заметная
4)
Оценка достоверности связи
Оценка достоверности линейной связи проводится на основе проверки значимости линейного коэффициента корреляции с помощью t-критерия Стьюдента:
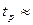 6,96 6,96
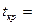 2,306 (по таблицам распределения Стьюдента при уровне значимости α = 0,05 и n-2), 2,306 (по таблицам распределения Стьюдента при уровне значимости α = 0,05 и n-2),
так как 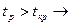 связь между факторным и результативным признаками – достоверна, а построенная модель – надежна. связь между факторным и результативным признаками – достоверна, а построенная модель – надежна.
5)
Интерпретация модели
Интерпретация заключается в статистической оценке модели и включенного в неё факторного признака, т.е в выяснении, как факторный признак влияет на результативный: чем больше величина коэффициента регрессии, тем значительнее влияние на результат.
Для расширения возможностей экономического анализа рассчитывается коэффициент эластичности 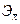 . .
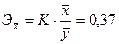
К
– коэффициент регрессии (в линейной модели К =
b
), показывающий на сколько процентов в среднем изменится значение результативного признака при изменении факторного на 1%.
В данном случае:
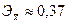 – это 37% – это 37%
Вывод
В ходе работы корреляционная связь была исследована в следующей последовательности:
1. Выявление связи между признаками.
2. Описание связи в табличной, графической и аналитической форме.
3. Измерение тесноты связи.
4. Оценка достоверности связи.
5. Интерпретация модели.
По исходным данным было построено корреляционное поле, и установлен факт наличия связи между факторным и результативным признаками. На основе анализа графически представлена корреляционная модель, построенная с помощью полинома первого порядка. Рассчитав показатель тесноты связи и квалифицировав его по шкале Чеддока, пришли к выводу, что связь заметная (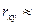 0,58 ). А, оценив достоверность по критерию Стьюдента ( 0,58 ). А, оценив достоверность по критерию Стьюдента (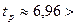 t
кр
=2,306
), убедились: связь между признаками достоверна, построенная модель – надежна. Полученный коэффициент эластичности показал, что в среднем на 37 % изменяется значение результативного признака при изменении факторного на 1%. t
кр
=2,306
), убедились: связь между признаками достоверна, построенная модель – надежна. Полученный коэффициент эластичности показал, что в среднем на 37 % изменяется значение результативного признака при изменении факторного на 1%.
|