Федеральное агентство по образованию
Бийский технологический институт (филиал)
государственного образовательного учреждения
высшего профессионального образования
«Алтайский государственный технический университет им. И.И. Ползунова»
(БТИ АлтГТУ)
КАФЕДРА
Информационных и управляющих систем
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
К КУРСОВОМУ ПРОЕКТУ (РАБОТЕ)
«Генерирование псевдослучайных чисел. Метод середины квадрата»
2009
Введение
Курсовая работа состоит из двух основных частей: теоретической и практической. В теоретической будет рассмотрено понятие вероятностного алгоритма, понятие «генератор случайных чисел», применение, методы генерирования случайных чисел, псевдослучайные числа, немного истории о генерировании случайных чисел и методе середины квадрата. В практической – рассмотрение и реализация метода середины квадрата, для этого работа разбита на несколько частей:
1. формулировка задачи.
2. построение модели
3. разработка алгоритма
4. кодирование (реализация) алгоритма
5. анализ сложности
6. проверка правильности
Теоретическая часть
Алгоритм называется вероятностным (randomized), если он использует генератор случайных чисел (random – numbergenerator). Это классическое определение, дается в большинстве литературных источников (в нашем случае Т. Кормен, Ч. Лейзерсон, Р. Ривест). Примерная работа генератора выглядит так: Random[a, b] возвращает с равной вероятностью любое целое число в интервале от а до b. Например Random[0,1] возвращает 0 или 1с вероятностью 1/2 чаще на практике используют генератор псевдослучайных чисел (pseudorandom – numbergenerator) – детерминированный алгоритм, который выдает числа, похожие на случайные.
Кроме того, генераторы случайных чисел называют датчиками случайных чисел – это могут быть разнообразные технические устройства, которые способны вырабатывать случайные величины. Используем пример, приведенный в опорном литературном источнике (А.В. Налимов, Основы алгоритмизации) – использование шумящих радиоэлектронных приборов (диоды, транзисторы). При работе такого прибора будем считать, сколько раз v
за фиксированное время Δt напряжение превысило заданный уровень E0.
двоичное случайное число получаем при помощи соотношения µ=vmod 2. если частоты появления 0 и 1 равны, то можно считать, что устройство вырабатывает случайную последовательность двоичных цифр. Если же частоты не равны то вводим какую-нибудь схему стабилизации: группировать цифры парами, тройками, и т.д., а значение 0 и 1 приписывать некоторым комбинациям.
Реклама

Обычно датчики содержат несколько генераторов описанного типа, работающих независимо друг от друга. Так что датчиком выдается число 0, а1
…аm
, записанное в форме m-разрядной двоичной дроби.
Что касается псевдослучайных чисел, возьмем любую случайную величину z
,
значения z1
,…, zn
, которые вычисляются по какой-либо заданной формуле и могут быть использованы вместо случайных чисел при решении некоторых задач, называются псевдослучайными. Одним из преимуществ псевдослучайных чисел является их быстрая генерация, к тому же они не требуют запоминающих устройств. Запас псевдослучайных чисел ограничен. В качестве стандартных обычно равномерно распределенные на интервале [0,1] псевдослучайные числа.
Рассмотрим так же понятие равномерного распределения. Равномерным распределением на конечном множестве чисел называется такое распределение, при котором любое из возможных чисел имеет одинаковую вероятность появления. Если не задано определенное распределение на конечном множестве чисел, то принято считать его равномерным.
Большинство алгоритмов вычисления случайных (псевдослучайных) чисел, используемых при практических расчетах, основаны на рекуррентных формулах первого порядка: γn+1
=Φ(γn
),где γo
задано. Гладкая функция y
=Φ(x)
не может породить хорошую последовательность псевдослучайных чисел, т. к. если при
помощи действительно случайных чисел нанести точки с координатами (γ1
,
γ2
)
; (γ2
,
γ3
)
;…; (γn
,
γn
+1
)
; на квадрат [(0,1)*(0,1)], то точки (
γ1
,
Φ(γ1
))
; (
γ2
,
Φ(γ2
));…; (
γn
,
Φ(γn
))
;… На основе этогоположения можно сформулировать условие относительно функции Φ(x).
Что бы функция y
=Φ(x)
порождала псевдослучайные числа, ее график должен плотно заполнять квадрат [(0,1)*(0,1)] т.е. она должна быть разрывной в каждой точке. Поскольку равномерно распределенные случайные числа должны довлетворять статистическим требованиям (например, математическое ожидание равно 0,5, дисперсия равна 1/12и т.д.), то условие плотного заполнения всего квадрата является только необходимым. Еще одна особенность алгоритмов типа γ
n
+1
=
Φ(γn
)
заключается в том, что они всегда порождают периодические последовательности. Следовательно существуют такие L и l, что γL
+
i
=
γl
+
i
, (i=1,2…). Пусть теперь L – наименьшее число, удовлетворяющее последнему равенству и такое, что l<L. Существует множество генераторов псевдослучайных чисел. Практически все алгоритмы генерирования псевдослучайных чисел ориентированы на конкретные машины (учитывают особенности работы процессора и способы хранения информации) и компиляторы (учитываются особенности арифметики, реализованной в конкретном языке программирования для конкретной машины). Поэтому готовые генераторы псевдослучайных чисел перед использованием необходимо тщательно проверить и настроить их на конкретные условия.
Реклама

Каждая из 10 цифр от 0 до 9 будет появляться примерно один раз из 10 в равномерной последовательности случайных цифр. Каждой паре двух последовательных цифр следует появиться 1 раз из 100 и т.д. однако если взять конкретную случайную последовательность длиной в миллион цифр, то она не всегда будет содержать 100 000 нулей, 100 000 единиц и т.д. Действительно, возможность появления такой последовательности незначительна; на самом деле, если рассматривать достаточно большую совокупность таких последовательностей, то в среднем будет появляться 100 000 нулей, 100 000 единиц и т.д.
Любая конкретная последовательность, содержащая миллион цифр, так же вероятна, как и любая другая. Если мы выберем миллион цифр наудачу и если окажется, что первые 999 999 из них – нули, то вероятность того, что последняя цифра в этой последовательности – также нуль, все еще останется точно равной одной десятой в истинно случайной ситуации. Это утверждение, хоть и кажется парадоксальным, не противоречит реальности.
Несовершенство первых механических методов в вначале пробудило интерес к получению случайных чисел с помощью обычных арифметических операций, заложенных в компьютер. Джон фон Нейман первым предложил такой подход около 1946 года; его идея заключалась в том, чтобы возвести в квадрат предыдущее случайное число и выделить средние цифры. Например, мы хотим получить 10-значное число и предыдущее равнялось 5772156649. возводим его в квадрат и получаем 33317792380594909201, значит следующим числом будет 7923805949.
Метод середин квадратов фон Неймана, как было показано, фактически является сравнительно бедным источником случайных чисел. Опасность состоит в том, что последовательность стремиться войти в привычную колею, т.е. короткий цикл повторяющихся элементов. Например, каждое появление нуля как числа последовательности приведет к тому, что все последующие числа также будут нулями.
Некоторые ученые экспериментировали с методом середин квадратов в начале 50-х годов. Работая с четырехзначными числами вместо десятизначных, Дж.Э. Форсайт испытал 16 различных начальных значений и обнаружил, что 12 из них приводят к циклическим последовательностям, заканчивающимся циклом 6100, 2100, 4100, 8100, 6100,…, в то время как две из них приводят к последовательностям, вырождающимся в 0. более интенсивные исследования, главным образом в двоичной системе счисления, провел Н.К. Метрополис. Он показал, что если использовать 20-разрядное число, то последовательность случайных чисел, полученная методом середин квадратов, вырождается в 13 различных циклов, причем длина самого большого периода равна 142.
Достаточно легко запустить метод середин квадратов с новым исходным значением, если обнаружить число 0, однако избавиться от длинных циклов довольно трудно.
Практическая часть
Метод середины квадрата
Формулировка задачи
Этот алгоритм является одним из первых и предложен Дж. Нейманом. Пусть числа γn
2kзначимые, т.е. γ
n
=0, а1, а2,… а2k.
Тогда функцию Φ(γn
) определим
следующимобразом:γn+1
=Φ(γn
)=Franc{10-2k
*Int(103k
*γ2
n
)} т.е. возведемγ
n
вквадратиполучим.γ
n
2
=
0, b1
, b2
,… b4k
. Затем отберем средние 2k цифр и получим γn
+1
=0, bk
+1
b2
…b3
k
. Теперь перейдем к более детальному рассмотрению алгоритма.
В результате работы программы должны получить математическое ожидание и дисперсию, определенные для последовательности из 50 000 элементов. Дана последовательность из 50 000 элементов. По ходу решения генерируем 2k – разрядные псевдослучайные числа. На входе должно быть задано х0
-2k разрядное начальное число. М – последовательность случайных чисел. Есть вероятность, что числа, генерируемые при помощи алгоритма обнулятся, при условии х0
< 104
. чтобы избежать этого нужно длину отрезка апериодичности L увеличить, что подробно будет рассмотрено ниже.
Построение модели
Случайная величина γ равномерно распределена на интервале [0,1], если определяются соотношениями:
Рγ
(γ)=1, γ∊[0,1]; Fγ
(γ)=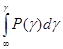
Математическое ожидание  и дисперсия (среднеквадратическое отклонение) и дисперсия (среднеквадратическое отклонение) 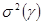 для непрерывных и дискретных случайных величин: для непрерывных и дискретных случайных величин:
 = =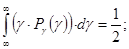
 = =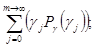
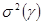 = =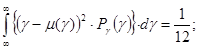
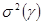 = =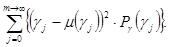
Теперь об упомянутом увеличении длины отрезка апериодичности. Есть вероятность, что числа, генерируемые при помощи алгоритма обнулятся, при условии х0
< 104
. чтобы избежать этого нужно длину отрезка апериодичности L увеличить. Практические расчеты показали, что L (длина отрезка апериодичности) достаточно мала, и это может явиться причиной отказа от алгоритма середины квадрата. Длину отрезка апериодичности можно несколько увеличить, если при выполнении условия 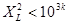 в качестве следующего случайного числа взять в качестве следующего случайного числа взять
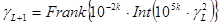
Теперь функция γn
примет следующий вид:
Φ(γn
)=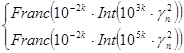 if if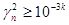 , , 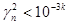
Для реализации алгоритма нужно определить наибольшее возможное значение k(чем больше это число, тем больше число значащих разрядов, а, следовательно, и длина отрезка апериодичности).
Таким образом, для обеспечения максимальной длины отрезка апериодичности нужно, используя простейшие типы данных, выбрать такие, которые обеспечивают наибольшее значение для k.
Например, можно принять, что γn
есть величина типа Single, а 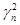 типа Double. При длине слова в 32 бита (1 разряд для знака; 7 бит для характеристики СС и 24 разряда под мантиссу ffffff типа Double. При длине слова в 32 бита (1 разряд для знака; 7 бит для характеристики СС и 24 разряда под мантиссу ffffff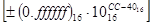 ) мантисса может принимать 210
*2 10
*2 4
=1024*1024*32 различных значения, что соответствует 7…8 значащим цифрам. ) мантисса может принимать 210
*2 10
*2 4
=1024*1024*32 различных значения, что соответствует 7…8 значащим цифрам.
При длине слова в 64 бита под мантиссу отводится 24+32 разряда. При помощи 56 разрядов можно закодировать 256
=(1024)5
*64, что соответствует 15..16 значащим цифрам. Таким образом, при величинах такого типа максимально возможное значение k равно 3 (т. к. 2k<7; 4k<15).
Разработка алгоритма
Приступим к разработке алгоритма.
Алгоритм seredina [середина квадрата]
Шаг0 [инициализация] х:=х0
;
Шаг1 [цикл, вычисление последовательности M случайных чисел х [1..M].]
For j:=1 to M do [окончаниешаг2 и stop]
Шаг2 [генерация нового случайного числа]
Y:=X2
[Y имеет 4k разрядов]
Число Х получаем удалением по k разрядов с каждого конца Y
X[j]:=X;
При k=2 и х0
=0.2134 в соответствии с первым оператором Шаг2 получим Y=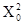 =0.04 5539 56. после применения второго оператора х1
=0.5539. если х0
<104
, то все числа, генерируемые при помощи данного алгоритма, будут тождественно равны нулю. Здесь нужно осуществлять описанное выше увеличение отрезка апериодичности. =0.04 5539 56. после применения второго оператора х1
=0.5539. если х0
<104
, то все числа, генерируемые при помощи данного алгоритма, будут тождественно равны нулю. Здесь нужно осуществлять описанное выше увеличение отрезка апериодичности.
Для реализации алгоритма потребуется написать процедуру, реализующую метод середины квадрата, которую назовем Rand, в которой при первом обращении задается целое число IX из [0.999999] и между вызовами оно не должно меняться. На выходе имеем числа: Rand числа типа Single из (0,1), IX числа типа LongInt из (0,999999), K числа типа LongInt из (0, К+1). Далее зададим переменные. Обнулим 7 и далее разряды числа Х, вычислим квадрат Х. Выберем 4…9 разряды числа Y. Определим новое целое случайное число IX из [0.999999] и случайную величину из [0.1]. Вычислим число К из [0.K+1].
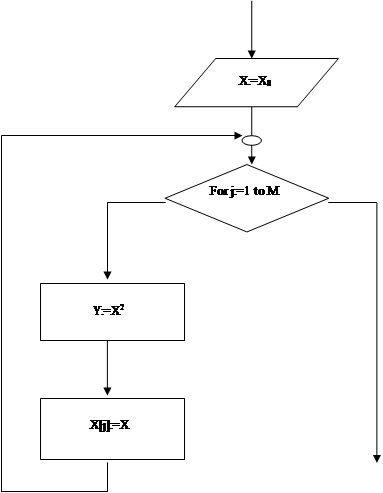
Рисунок 1. блок-схем программы
 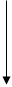    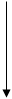 Нет Нет  Да Да
z:=y*1.e+6; y:=z1-Trunc(z1)
|
|

Рисунок 2. блок-схема процедуры Rand
Кодирование алгоритма
Programseredina {метод середины квадрата}
Usescrt;
Var
Urand: Single;
Dm, Dd: Double;
n, i, j, k, l, ll: LongInt;
F: Text;
Procedure Rand (var Ix, k: LongInt; Urand: Single);
Var
x, z: Single;
y, z1: Double; i: LongInt;
Begin
z:=Ix; x:=z{*1.e-6}; {обнулим 7 и далее разряды числа Х.}
z1:=x+1.e-6; y:=z1*z1*1.e-12; {вычислим квадрат Х.}
z1:=y*1.e+3; y:=z1-Trunc(z1); {выберем 4…9 разряды числа Y.}
if y<1.e-6 then
Begin
z1:=y*1.e+6;
y:=z1-Trunc(z1);
End;
z1:=y*1.e+6;
y:=Trunc(z1);
Ix:=Trunc(y); y:=y*1.e-6; Urand:=y;
{определили новое целое случайное число IX из [0.999999] и случайную величину из [0.1]}
k:=Round((k+1)*y); {вычисляем число К из [0, К+1]}
End; {Rand}
Begin
Clrscr;
Assign (F, ’d:/F/Rand.dat’);
Rewrite(F);
n:=3–23; Dm:=0; Dd:=0; ll:=50000;
for l:=1 to ll do
begin
k:=100;
Rand (n, k, Urand);
Dm:=Dm+Urand/ll;
Dd:=Dd+(Urand-0.5)*(Urand-0.5)/ll;
End;
Writeln (F, ’M=’, Dm, ’Sig^2=’, Dd);
Close(F);
End.
В результате работы алгоритма, после создания текстового файла по указанному адресу, получаем файл Rand, содержащий результат – математическое ожидание и дисперсию.
Анализ сложности алгоритма
Для этого воспользуемся способом, заключающимся в подсчете арифметических операций, необходимых для выполнения алгоритма (в этом случае определяется рабочая функция).
Пусть G(n) – алгоритм для решения некоторого класса задач, а n – размерность размерность отдельной задачи из этого класса. Определим 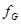 (n) как рабочую функцию, дающую верхнюю границу для максимального числа основных операций, которые должен выполнить алгоритм G(n) для решения любой задачи размерности n. (n) как рабочую функцию, дающую верхнюю границу для максимального числа основных операций, которые должен выполнить алгоритм G(n) для решения любой задачи размерности n.
Алгоритм G(n) полиномиальный, если 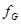 (n) растет не быстрее, чем полином от n, в противном случае алгоритм экспоненциальный. (n) растет не быстрее, чем полином от n, в противном случае алгоритм экспоненциальный.
Функцию f
(n) определяют как О и говорят, что она порядка g
(
n
)
для больших n, если и говорят, что она порядка g
(
n
)
для больших n, если 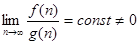
Функция h
(n) является О для больших n, если для больших n, если 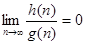
Если f
(n) есть О , то эти две функции возрастают с одинаковой скоростью при n
→∞. Если f
(n) есть О , то эти две функции возрастают с одинаковой скоростью при n
→∞. Если f
(n) есть О , то g
(
n
)
возрастает гораздо быстрее, чем f
(n). , то g
(
n
)
возрастает гораздо быстрее, чем f
(n).
Алгоритм G(n) называется полиномиальным, если 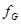 (n)= О (n)= О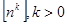 , в противном случае алгоритм является экспоненциальным. , в противном случае алгоритм является экспоненциальным.
Рассмотрим процедуру Rand. В ней всего 4 шага, одно сравнение. Для процедуры G(n) рабочая функция имеет вид 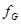 (n)= О(n) и она является полиномиальной. (n)= О(n) и она является полиномиальной.
Проверка правильности программы
Анализ структуры программы
Для этого воспользуемся управляющим графом (ориентированный граф, вершины которого – операторы, а дуги соединяют операторы, между которыми возможна передача управления).
6 7 8 9 10 11 12 14
  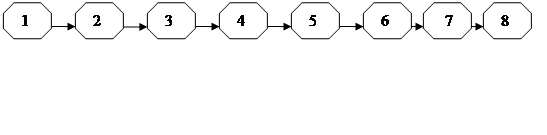
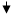 22 21 20 19 18 17 15 22 21 20 19 18 17 15
       Рисунок 4. Схема Мартынюка Рисунок 4. Схема Мартынюка
На приведенной выше схеме Мартынюка путь является простым, так как он не содержит ни одной вершины или дуги более одного раза. Схема правильная, так как выполняется условие, что каждая вершина принадлежит хотя бы одному пути по графу.
Таблица 2. Матрица Путей
Матрица путей С – путей длины 1.
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
| 1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 2 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 3 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 4 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 5 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 6 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 7 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
| 8 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
| 9 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
| 10 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
| 11 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
| 12 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
| 13 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
| 14 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
| 15 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Рис. 6
Таблица 3. Матрица Путей
Матрица Р – матрица всех путей
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
| 1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 2 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 3 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 4 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 5 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 6 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 7 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 8 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 9 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
| 10 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
| 11 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
| 12 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
| 13 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
| 14 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
| 15 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Все элементы 1 столбца равны 1, значит в 1 вершину управление не передается ни из какой другой. Все элементы 1 строки равны 1, значит из 1 вершины управление не передается ни в какую другую, отсюда следует, что схема программы является правильной.
Проверка диапазона значений переменных
Dm– математическое ожидание, Dm: Dm+Urand/ll;
Dd – дисперсия, Dd: Dd+Urand;
k: Round((k+1)*y);
L: array [1..50 000];
ll: 50 000;
Ix: Trunc(y);
Urand: y;
X: z;
Z: Ix;
Y: z1*z1z*1.e-12, z1-Trunc(z1), Trunc(z1);
Z1: x+1.e-6, y*1.e+3, y*1.e+6.
Тестирование программы
Проверка входных данных. N:=3–23, Dm:=0, Dd:=0, ll:=50000, l:=[1..ll], k:=10. все входные данные обрабатываются верно.
Список литературы
1. Основы алгоритмизации, учебное пособие. А.В. Налимов. Барнаул 2000 г.
2. Анализ и разработка алгоритмов, методические рекомендации. А.В. Налимов. Барнаул 2001 г.
3. Алгоритмы построение и анализ, Т. Кормен, Ч. Лейзерсон, Р. Ривест. Москва 2007 г.
4. Алгоритмы дискретной математики, Л.Е. Захарова. Москва 2007 г.
5. Искусство программирования, Д.Э. Кнут. Том 2.
|