Контрольная работа №1.
Вариант 8.
Задание 1.
Однажды вечером Ваня и Тима сели играть в кости. Они по очереди бросали две игральные кости. Если сумма выпавших очков равнялась 7, то выигрывал Ваня, а если сумма очков равнялась 8, то выигрывал Тима. На кого бы из них Вы поставили, если бы Вам пришлось держать пари?
Решение.
Посчитаем число 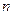 всевозможных исходов при одном бросании двух игральных костей. всевозможных исходов при одном бросании двух игральных костей.
При одном бросании двух игральных костей пространство всевозможных исходов 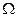 имеет следующий вид имеет следующий вид 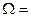 {11, 12, 13, 14, 15, 16, 21, 22, 23, 24, 25, 26, 31, 32, 33,34, 35, 36, 41, 42, 43, 44, 45, 46, 51, 52, 53, 54, 55, 56, 61, 62, 63, 64, 65, 66}. Пространство всевозможных исходов {11, 12, 13, 14, 15, 16, 21, 22, 23, 24, 25, 26, 31, 32, 33,34, 35, 36, 41, 42, 43, 44, 45, 46, 51, 52, 53, 54, 55, 56, 61, 62, 63, 64, 65, 66}. Пространство всевозможных исходов 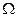 состоит из 36 элементов. Следовательно, состоит из 36 элементов. Следовательно, 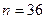 . .
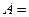 {сумма очков равнялась 7} {сумма очков равнялась 7}
Посчитаем число 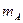 исходов, благоприятных событию исходов, благоприятных событию 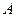 . .
Пространство исходов, благоприятных событию 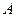 , имеет следующий вид , имеет следующий вид 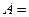 {16, 25, 34, 43, 52, 61}. Пространство исходов, благоприятных событию {16, 25, 34, 43, 52, 61}. Пространство исходов, благоприятных событию 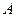 , состоит из 6 элементов. Следовательно, , состоит из 6 элементов. Следовательно, 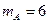 . .
По классическому определению вероятности 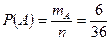 . .
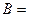 {сумма очков равнялась 8} {сумма очков равнялась 8}
Посчитаем число 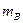 исходов, благоприятных событию исходов, благоприятных событию 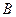 . .
Пространство исходов, благоприятных событию 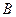 , имеет следующий вид , имеет следующий вид 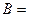 {26, 35, 44, 53, 62}. Пространство исходов, благоприятных событию {26, 35, 44, 53, 62}. Пространство исходов, благоприятных событию 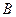 , состоит из 5 элементов. Следовательно, , состоит из 5 элементов. Следовательно, 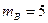 . .
По классическому определению вероятности 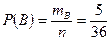 . .
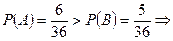 Вероятнее всего, что выиграет Ваня. Вероятнее всего, что выиграет Ваня.
Ответ.
На Ваню.
Задание 2.
Теща Кисы Воробьянинова зашила фамильные бриллианты в один из двенадцати одинаковых стульев. Два из них в последствии остались в Старгороде, а десять стульев отправились в Москву. Какова вероятность отыскать бриллианты в одном из двух стульев, оставшихся в Старгороде?
Решение.
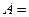 {бриллианты в одном из двух стульев, оставшихся в Старгороде} {бриллианты в одном из двух стульев, оставшихся в Старгороде}
Посчитаем число 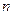 всевозможных исходов. Бриллианты могут находиться в одном из 12 одинаковых стульев. Следовательно, всевозможных исходов. Бриллианты могут находиться в одном из 12 одинаковых стульев. Следовательно, 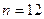 . .
Посчитаем число 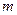 исходов, благоприятных событию исходов, благоприятных событию 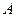 . Благоприятным событием является то, что бриллианты находятся в одном из 2 стульев, оставшихся в Старгороде. Следовательно, . Благоприятным событием является то, что бриллианты находятся в одном из 2 стульев, оставшихся в Старгороде. Следовательно, 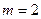 . .
По классическому определению вероятности 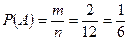 . .
Ответ.
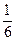
Задание 3.
Вероятность того, что рабочий перевыполнит план, равна 0.8, а вероятность того, что в случае перевыполнения плана он не получит премию, равна 0.1. Какова вероятность того, что рабочий получит премию?
Реклама

Решение.
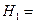 {рабочий перевыполнит план} {рабочий перевыполнит план}
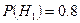
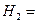 {рабочий не перевыполнит план} {рабочий не перевыполнит план}
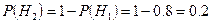
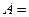 {рабочий получит премию} {рабочий получит премию}
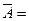 {рабочий не получит премию} {рабочий не получит премию}
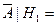 {рабочий не получит премию при условии, что он перевыполнит план} {рабочий не получит премию при условии, что он перевыполнит план}
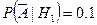
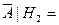 {рабочий не получит премию при условии, что он не перевыполнит план} {рабочий не получит премию при условии, что он не перевыполнит план}
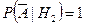
По формуле полной вероятности
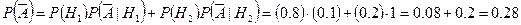
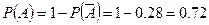
Ответ.
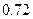
Задание 4.
Шахматист завершает вничью в среднем 20% своих партий. Определить наивероятнейшее число ничьих, которые сделает шахматист в турнире, где сыграет 12 партий.
Решение.
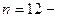 количество партий количество партий
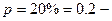 вероятность завершения одной отдельно взятой партии вничью вероятность завершения одной отдельно взятой партии вничью
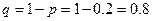
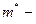 наивероятнейшее число партий, завершенных вничью наивероятнейшее число партий, завершенных вничью
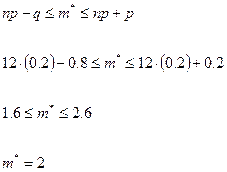
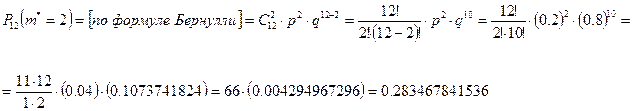
Ответ.
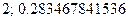
Задание 5.
Преподаватель проверяет контрольную по теории вероятностей, которую писали студенты трех групп. В первой группе неудовлетворительно написанные контрольные работы составляют 10%, во второй – 15%, в третьей – 20%. Определить вероятность попадания на проверку неудовлетворительно написанной работы, если всего было сдано 18 работ из первой группы, 20 – из второй и 24 из третьей группы.
Решение.
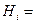 {работа из {работа из 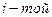 группы}; группы}; 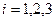
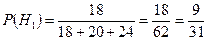
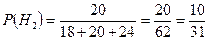
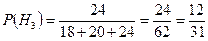
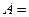 {на проверку попала неудовлетворительно написанная работа} {на проверку попала неудовлетворительно написанная работа}
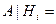 {на проверку попала неудовлетворительно написанная работа при условии, что она из {на проверку попала неудовлетворительно написанная работа при условии, что она из 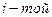 группы}; группы}; 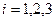

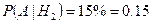
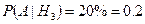
По формуле полной вероятности
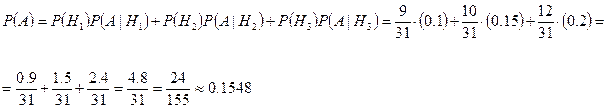
Ответ.
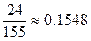
Контрольная работа №2.
Вариант 8.
Задание 1.
В урне 3 черных и 2 белых шара. Производится последовательное без возвращения извлечение шаров до появления черного. Составить закон распределения случайной величины 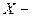 числа извлеченных шаров. Вычислить математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины. числа извлеченных шаров. Вычислить математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины.
Решение.
Случайная величина 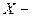 число извлеченных шаров до появления черного шара. Данная случайная величина может принимать следующие значения: число извлеченных шаров до появления черного шара. Данная случайная величина может принимать следующие значения:
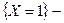 первый извлеченный шар оказался черным первый извлеченный шар оказался черным
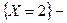 первый извлеченный шар – белый, а второй извлеченный шар оказался черным первый извлеченный шар – белый, а второй извлеченный шар оказался черным
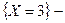 первые и второй извлеченные шары- белые, а третий извлеченный шар оказался черным первые и второй извлеченные шары- белые, а третий извлеченный шар оказался черным
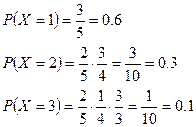
Закон распределения случайной величины 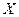 имеет следующий вид: имеет следующий вид:
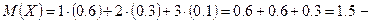 математическое ожидание математическое ожидание
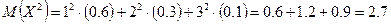
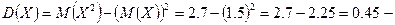 дисперсия дисперсия
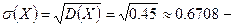 среднеквадратическое отклонение среднеквадратическое отклонение
Ответ.

Задание 2.
Случайная величина 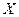 задана функцией распределения задана функцией распределения 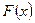 . Найти плотность распределения, математическое ожидание, дисперсию, а также вероятность попадания случайной величины в интервал . Найти плотность распределения, математическое ожидание, дисперсию, а также вероятность попадания случайной величины в интервал 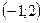 . Построить графики функций . Построить графики функций 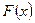 и и 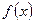 . .
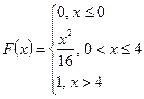
Решение.
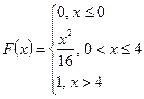
График функции распределения 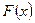 представлен ниже. представлен ниже.
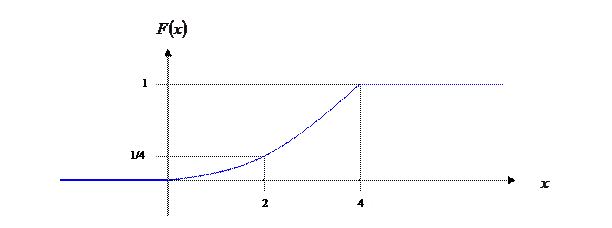
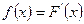
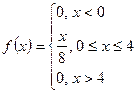
График плотности распределения 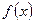 представлен ниже. представлен ниже.
Реклама

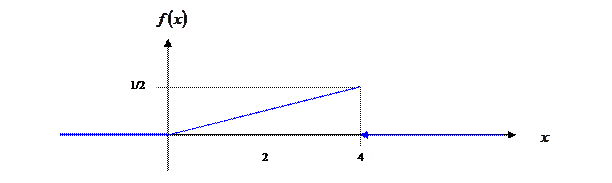
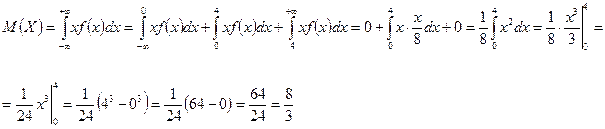
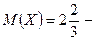 математическое ожидание математическое ожидание
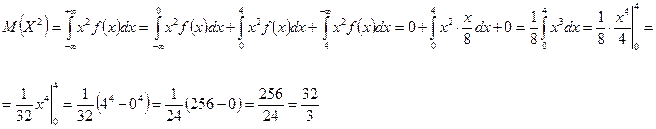
 дисперсия дисперсия
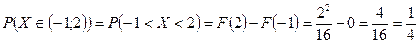
Ответ.
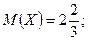  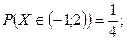 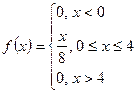
|