1. Предмет и задачи исследования операций в экономике. Основные понятия теории исследования операций.
Предмет исследования операций - системы организационного управления или организации, которые состоят из большого числа взаимодействующих между собой подразделений не всегда согласующихся между собой и могут быть противоположны.
Цель исследования операций - количественное обоснование принимаемых решений по управлению организациями
Решение, которое оказывается наиболее выгодным для всей организации называется оптимальным, а решение наиболее выгодное одному или нескольким подразделениям будет субоптимальным.
Исследование операций - наука, занимающаяся разработкой и практическим применением методов наиболее оптимального управления организационными системами.
Операцией называется всякое мероприятие (система действий), объединенное единым замыслом и направленное к достижению какой-то цели.
Цель исследования операций - предварительное количественное обоснование оптимальных решений.
Всякий определенный выбор зависящих от нас параметров называется решением. Оптимальным называются решения, по тем или другим признакам предпочтительные перед другими.
Параметры, совокупность которых образует решение, называются элементами решения.
Множеством допустимых решений называются заданные условия, которые фиксированы и не могут быть нарушены.
Показатель эффективности - количественная мера, позволяющая сравнивать разные решения по эффективности.
2. Понятие о сетевом планировании и управлении. Сетевая модель процесса и ее элементы.
Метод работы с сетевыми графиками – сетевое планирование – базируется на теории графов. В переводе с греческого граф (grafpho – пишу) представляет систему точек, некоторые из них соединены линиями – дугами (или ребрами). Это топологическая (математическая) модель взаимодействующих систем. С помощью графов можно решать не только задачи сетевого планирования, но и другие задачи. Метод сетевого планирования применяется при планировании проведения комплекса взаимосвязанных работ. Он позволяет наглядно представить организационно-технологическую последовательность выполнения работ и установить взаимосвязь между ними. Кроме этого, он позволяет обеспечить координацию операций различной степени сложности и выявить операции, от которых зависит продолжительность всей работы (т.е. организационного мероприятия), а также сосредоточить внимание на своевременном выполнении каждой операции.
Реклама

Основой сетевого планирования и управления является сетевая модель (СМ), в которой моделируется совокупность взаимосвязанных работ и событий, отображающих процесс достижения определенной цели. Она может быть представлена в виде графика или таблицы.
Основные понятия сетевой модели:
- событие, работа, путь.
Событиями называются результаты выполнения одной или нескольких работ. Они не имеют протяженности во времени.
Путь — это цепочка следующих друг за другом работ, соединяющих начальную и конечную вершины.
Продолжительность пути определяется суммой продолжительностей составляющих его работ.
3. Построение и упорядочивание сетевого графика.
В качестве модели, отражающей технологические и организационные взаимосвязи процесса производства строительно-монтажных работ в системах сетевого планирования и управления (СПУ), используется сетевая модель.
Сетевой моделью называется графическое изображение процессов, выполнение которых приводит к достижению одной или нескольких поставленных целей, с указанием установленных взаимосвязей между этими процессами. Сетевой график представляет собой сетевую модель с расчетными временными параметрами.
Структура сетевого графика, определяющая взаимную зависимость работ и событий, называется его топологией.
Работа - это производственный процесс, требующий затрат времени, труда и материальных ресурсов, который при его выполнении приводит к достижению определенных результатов.
Зависимость (фиктивная работа), не требующая затрат времени изображается пунктирной стрелкой. Фиктивная работа используется в сетевом графике для отражения связей между событиями и работами.
В сетевом графике применяются временные, стоимостные и другие характеристики работ.
Продолжительной работы – время выполнения данной работы в рабочих днях или других единицах времени, одинаковых для всех работ сетевого графика. Продолжительность работ может быть как определенной (детерминированной), так и случайной величиной, задаваемой законом ее распределения.
Стоимость работы – это прямые затраты, необходимые для ее выполнения, зависящие от длительности и условий выполнения этой работы.
Ресурсы характеризуются потребностью в физических единицах, необходимых для выполнения данной работы.
Реклама

Качество, надежность и другие показатели работ служат дополнительными характеристиками работ.
Событие - это факт окончания одной или нескольких работ, необходимый и достаточный для начала одной или нескольких последующих работ. Каждому событию присваивается номер, называемый кодом. Каждая работа определяется двумя событиями: кодом начального события, обозначаемого i и кодом конечного события, обозначаемого буквой j.
События, не имеющие предшествующих работ, называются начальными; события, не имеющие последующих – конечными.
1 Направление построения сети может иметь различный характер. Сетевой график может строиться от начального события к завершающему и от завершающего к исходному (начальному), а также от любого из событий к исходному или конечному.
2 При построении сети решаются вопросы:
- какие работы (работу) необходимо выполнить, чтобы начать данную работу;
- какие работы целесообразно выполнять параллельно с данной работой;
3 Первоначальный сетевой график строится без учета продолжительности работ, составляющих сеть.
4 Форма графика должна быть простой и зрительно легко воспринимаемой.
5 Между двумя событиями может заключаться только одна работа. При строительстве зданий и сооружений работы могут выполняться последовательно, параллельно или одновременно, часть последовательно, а часть параллельно, в результате чего между отдельными работами складываются различные зависимости.
Нумерация (кодирование) событий производится после окончания построения сети, начиная от исходного события до конечного.
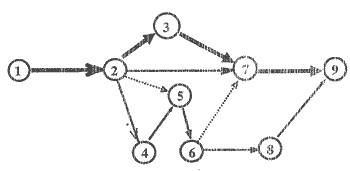
4. Критический путь сетевого графика. Резервы времени. Ранние и поздние сроки событий и работ в сетевом графике.
В сетевом графике между начальным и конечным событиями может быть несколько путей. Путь, имеющий наибольшую продолжительность, называется критическим. Критический путь определяет общую продолжительность работ. Все остальные пути имеют меньшую продолжительность, и поэтому в них выполняемое работы имеют резервы времени.
Критический путь обозначается на сетевом графике утолщенными или двойными линиями (стрелками).
Особое значение при составлении сетевого графика имеют два понятия:
Раннее начало работы - срок, раньше которого нельзя начать данную работу, не нарушив принятой технологической последовательности. Он определяется наиболее долгим путем от исходного события до начала данной работы
Позднее окончание работы - самый поздний срок окончания работы, при котором не увеличивается общая продолжительность работ. Он определяется самым коротким путем от данного события до завершения всех работ.
Раннее окончание - срок, раньше которого нельзя закончить данную работу. Он равен раннему началу плюс продолжительность данной работы
Позднее начало - срок, позже которого нельзя начинать данную работу, не увеличив общую продолжительность строительства. Он равен позднему окончанию минус продолжительность данной работы.
Если событие является окончанием лишь одной работы (т.е. в него направлена только одна стрелка), то раннее окончание этой работы совпадает с ранним началом последующей.
Общий (полный) резерв - это наибольшее время, на которое можно задержать выполнение данной работы, не увеличивая общую продолжительность работ. Он определяется разностью между поздним и ранним началом (или поздним и ранним окончанием - что то же самое).
Частный (свободный) резерв - это наибольшее время, на которое можно задержать выполнение данной работы, не меняя раннего начала последующей. Этот резерв возможен только тогда, когда в событие входят две или более работы (зависимости), т.е. на него направлены две или более стрелки (сплошные или пунктирные). Тогда лишь у одной из этих работ раннее окончание будет совпадать с ранним началом последующей работы, для остальных же это будут разные значения. Эта разница у каждой работы и будет ее частным резервом.
5. Динамическое программирование. Принцип оптимальности и управления Беллмана.
Динамическое программирование – один из наиболее мощных методов оптимизации. С задачами принятия рациональных решений, выбора наилучших вариантов, оптимального управления имеют дело специалисты разного профиля. Среди методов оптимизации динамическое программирование занимает особое положение. Этот метод исключительно привлекателен благодаря простоте и ясности своего основного принципа – принципа оптимальности. Сфера приложения принципа оптимальности чрезвычайно широка, круг задач, к которым он может быть применен, до настоящего времени еще полностью не очерчен. Динамическое программирование с самого начала выступает как средство практического решения задач оптимизации.
Кроме принципа оптимальности, основного приема исследования, большую роль в аппарате динамического программирования играет идея погружения конкретной задачи оптимизации в семейство аналогичных задач. Третьей его особенностью, выделяющей его среди других методов оптимизации, является форма конечного результата. Применение принципа оптимальности и принципа погружения в многошаговых, дискретных процессах приводят к рекуррентно-функцио-нальным уравнениям относительно оптимального значения критерия качества. Полученные уравнения позволяют последовательно выписать оптимальные управления для исходной задачи. Выигрыш здесь состоит в том, что задача вычисления управления для всего процесса разбивается на ряд более простых задач вычисления управления для отдельных этапов процесса.
Главным недостатком метода является, говоря словами Беллмана, «проклятие размерности» – его сложность катастрофически возрастает с увеличением размерности задачи.
6. Задача о распределении средств между предприятиями.
Можно сказать, что процедура построения оптимального управления методом динамического программирования распадается на две стадии: предварительную и окончательную. На предварительной стадии для каждого шага определяется УОУ зависящее от состояния системы (достигнутого в результате предыдущих шагов), и условно оптимальный выигрыш на всех оставшихся шагах, начиная с данного, также зависящий от состояния. На окончательной стадии определяется (безусловное) оптимальное управление для каждого шага. Предварительная (условная) оптимизация производится по шагам в обратном порядке: от последнего шага к первому; окончательная (безусловная) оптимизация — также по шагам, но в естественном порядке: от первого шага к последнему. Из двух стадий оптимизации несравненно более важной и трудоемкой является первая. После окончания первой стадии выполнение второй трудности не представляет: остается только "прочесть" рекомендации, уже заготовленные на первой стадии.
7. Постановка задачи линейного программирования.
Линейное программирование -- популярный инструмент решения экономических задач, которые характиризуются наличием одного критерия (например, максимизировать доход от производства продукции за счет оптимального выбора производственной программы, или , например, минимизировать транспортные расходы и пр.). Для экономических задач характерны ресурсные ограничения (материальные и / или финансовые). Они записываются в виде системы неравенств, иногда в виде равенств.
С точки зрения прогнозирования допустимых интервалов цен (или объемов продаж) в рамках обобщенного непараметрического метода , применение линейного программирования означает:
Критерием является MAX цена очередного продукта из интересуемой группы f.
Управляемыми переменными величинами являются цены всех продуктов из группы f.
Ограничениями в нашей задаче прогнозирования с использованием обобщенного непараметрического метода, являются :
a) система неравенств (ограничения рациональности поведения потребителя) (см. 4.2. Прогнозирование в рамках обобщенного непараметрического метода);
б) требование неотрицательности управляемых переменных (в нашей задаче прогнозирования мы потребуем, чтобы цены на продукты из группы f не опустились ниже 80% от значений цен в последней временной точке) ;
в) бюджетное ограничение в виде равенства - требование постоянства суммы затрат на покупку продуктов из группы f (с учетом 15% инфляции, например).
8. Графический метод решения задач линейного программирования.
Графический метод основан на геометрической интерпретации задачи линейного программирования и применяется в основном при решении задач двумерного пространства и только некоторых задач трехмерного простран6тва, так как довольно трудно построить многогранник решений, который образуется в результате пересечения полупространств. Задачу пространства размерности больше трех изобразить графически вообще невозможно.
Пусть задача линейного программирования задана в двумерном пространстве, т. е. ограничения содержат две переменные.
Найти минимальное значение функции
(2.1) Z = С1х1+С2х2
при
a11x1 + a22x2 b1
(2.2)a21x1 + a22x2 b2
aM1x1 + aM2x2 bM
(2.3) х1 0, х2 0
Допустим, что система (2.2) при условии (2.3) совместна и ее многоугольник решений ограничен. Каждое из неравенств (2.2) и (2.3), как отмечалось выше, определяет полуплоскость с граничными прямыми: ai1x1 + ai2x2 + ai3x3 = bi,(i = 1, 2, ..., n), х1=0, х2=0. Линейная функция (2.1) при фиксированных значениях Z является уравнением прямой линии: С1х1 + С2х2 = const. Построим многоугольник решений системы ограничений (2.2) и график линейной функции (2.1) при Z = 0 (рис. 2.1). Тогда поставленной задаче линейного прграммирования можно дать следующую интерпретацию. Найти точку многоугольника решений, в которой прямая С1х1 + С2х2 = const опорная и функция Z при этом достигает минимума.
Значения Z = С1х1 + С2х2 возрастают в направлении вектора N =(С1, С2), поэтому прямую Z = 0 передвигаем параллельно самой себе в направлении вектора Х. Из рис. 2.1 следует, что прямая дважды становится опорной по отношению к многоугольнику решений (в точках А и С), причем минимальное значение принимает в точке А. Координаты точки А (х1, х2) находим, решая систему уравнений прямых АВ и АЕ.
Если многоугольник решений представляет собой неограниченную многоугольную область, то возможны два случая.
Случай 1. Прямая С1х1 + С2х2 = const, передвигаясь в направлении вектора N или противоположно ему, постоянно пересекает многоугольник решений и ни в какой точке не является опорной к нему. В этом случае линейная функция не ограничена на многоугольнике решений как сверху, так и снизу (рис. 2.2).
Случай 2. Прямая, пере-двигаясь, все же становится опорной относительно многоу-гольника решений (рис. 2.2, а – 2.2, в). Тогда в зави-симости от вида области ли-нейная функция может быть ограниченной сверху и неограниченной снизу (рис. 2.2, а), ограниченной снизу и неограниченной сверху (рис. 2.2, б), либо ограниченной как снизу, так и сверху (рис. 2.2, в).
9. Симплекс- метод.
Симплекс-метод является основным в линейном программировании. Решение задачи начинается с рассмотрений одной из вершин многогранника условий. Если исследуемая вершина не соответствует максимуму (минимуму), то переходят к соседней, увеличивая значение функции цели при решении задачи на максимум и уменьшая при решении задачи на минимум. Таким образом, переход от одной вершины к другой улучшает значение функции цели. Так как число вершин многогранника ограничено, то за конечное число шагов гарантируется нахождение оптимального значения или установление того факта, что задача неразрешима.
Этот метод является универсальным, применимым к любой задаче линейного программирования в канонической форме. Система ограничений здесь - система линейных уравнений, в которой количество неизвестных больше количества уравнений. Если ранг системы равен r, то мы можем выбрать r неизвестных, которые выразим через остальные неизвестные. Для определенности предположим, что выбраны первые, идущие подряд, неизвестные X1, X2, ..., Xr. Тогда наша система уравнений может быть записана как
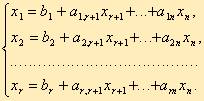
Симплекс-метод основан на теореме, которая называется фундаментальной теоремой симплекс-метода. Среди оптимальных планов задачи линейного программирования в канонической форме обязательно есть опорное решение ее системы ограничений. Если оптимальный план задачи единственен, то он совпадает с некоторым опорным решением. Различных опорных решений системы ограничений конечное число. Поэтому решение задачи в канонической форме можно было бы искать перебором опорных решений и выбором среди них того, для которого значение F самое большое. Но, во-первых, все опорные решения неизвестны и их нужно находить, a, во-вторых, в реальных задачах этих решений очень много и прямой перебор вряд ли возможен. Симплекс-метод представляет собой некоторую процедуру направленного перебора опорных решений. Исходя из некоторого, найденного заранее опорного решения по определенному алгоритму симплекс-метода мы подсчитываем новое опорное решение, на котором значение целевой функции F не меньше, чем на старом. После ряда шагов мы приходим к опорному решению, которое является оптимальным планом.
10. Постановка транспортной задачи. Методы определения опорных планов.
Имеется m пунктов отправления («поставщиков») и n пунктов потребления («потребителей») некоторого одинакового товара. Для каждого пункта определены:
ai – объемы производства i -го поставщика, i = 1, …, m;
вj – спрос j-го потребителя, j= 1,…,n;
сij – стоимость перевозки одной единицы продукции из пункта Ai– i-го поставщика, в пункт Вj – j-го потребителя.
Для наглядности данные удобно представлять в виде таблицы, которую называют таблицей стоимостей перевозок.
Требуется найти план перевозок, при котором бы полностью удовлетворялся спрос всех потребителей, при этом хватало бы запасов поставщиков и суммарные транспортные расходы были бы минимальными.
Под планом перевозок понимают объем перевозок, т.е. количество товара, которое необходимо перевезти от i-го поставщика к j-му потребителю. Для построения математической модели задачи необходимо ввести m·n штук переменных хij, i= 1,…, n, j= 1, …, m, каждая переменная хij обозначает объем перевозок из пункта Ai в пункт Вj. Набор переменных X = {xij} и будет планом, который необходимо найти, исходя из постановки задачи. 
Это условие для решения закрытых и открытых транспортных задач (ЗТЗ).
Очевидно, что для разрешимости задачи 1 необходимо, чтобы суммарный спрос не превышал объема производства у поставщиков:
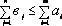
Если это неравенство выполняется строго, то задача называется «открытой» или «несбалансированной», если же 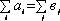 , то задача называется «закрытой» транспортной задачей, и будет иметь вид (2): , то задача называется «закрытой» транспортной задачей, и будет иметь вид (2):
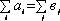 – условие сбалансированности. – условие сбалансированности.
Это условие для решения закрытых транспортных задач (ЗТЗ).
11. Алгоритм решения транспортной задачи.
Применение алгоритма требует соблюдения ряда предпосылок:
1. Должна быть известна стоимость перевозки единицы продукта из каждого пункта производства в каждый пункт назначения.
2. Запас продуктов в каждом пункте производства должен быть известен.
3. Потребности в продуктах в каждом пункте потребления должны быть известны.
4. Общее предложение должно быть равно общему спросу.
Алгоритм решения транспортной задачи состоит из четырех этапов:
Этап I. Представление данных в форме стандартной таблицы и поиск любого допустимого распределения ресурсов. Допустимым называется такое распределение ресурсов, которое позволяет удовлетворить весь спрос в пунктах назначения и вывезти весь запас продуктов из пунктов производства.
Этап 2. Проверка полученного распределения ресурсов на оптимальность
Этап 3. Если полученное распределение ресурсов не является оптимальным, то ресурсы перераспределяются, снижая стоимость транспортировки.
Этап 4. Повторная проверка оптимальности полученного распределения ресурсов.
Данный итеративный процесс повторяется до тех пор, пока не будет получено оптимальное решение.
12. Модели управления запасами.
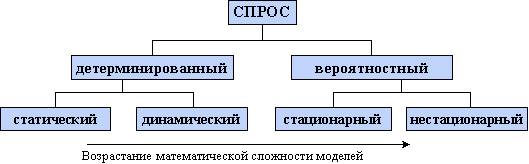
Несмотря на то, что любая модель управления запасами призвана отвечать на два основных вопроса (когда и сколько), имеется значительное число моделей, для построения которых используется разнообразный математический аппарат.
Такая ситуация объясняется различием исходных условий. Главным основанием для классификации моделей управления запасами является характер спроса на хранимую продукцию (напомним, что с точки зрения более общей градации сейчас мы рассматриваем лишь случаи с независимым спросом).
Итак, в зависимости от характера спроса модели управления запасами могут быть
детерминированными;
вероятностными.
В свою очередь детерминированный спрос может быть статическим, когда интенсивность потребления не изменяется во времени, или динамическим, когда достоверный спрос с течением времени может изменяться.
Вероятностный спрос может быть стационарным, когда плотность вероятности спроса не изменяется во времени, и нестационарным, где функция плотности вероятности меняется в зависимости от времени. Приведенную классификацию поясняет рисунок.
Наиболее простым является случай детерминированного статического спроса на продукцию. Однако такой вид потребления на практике встречается достаточно редко. Наиболее сложные модели - модели нестационарного типа.
Кроме характера спроса на продукцию при построении моделей управления запасами приходится учитывать множество других факторов, например:
сроки выполнения заказов. Продолжительность заготовительного периода может быть постоянной либо являться случайной величиной;
процесс пополнения запаса. Может быть мгновенным либо распределенным во времени;
наличие ограничений по оборотным средствам, складской площади т.п.
13. Системы массового обслуживания (СМО) и показатели их эффективности.
Системы массового обслуживания (СМО) представляют собой системы специального вида, реализующие многократное выполнение однотипных задач. Подобные системы играют важную роль во многих областях экономики, финансов, производства и быта. В качестве примеров СМО в финансово-экономической ; сфере можно привести банки различных типов (коммерческие, инвестиционные, ипотечные, инновационные, сберегательные), страховые организации, государственные акционерные общества, компании, фирмы, ассоциации, кооперативы, налоговые инспекции, аудиторские службы, различные системы связи (в том числе телефонные станции), погрузочно-разгрузочные комплексы (порты, товарные станции), автозаправочные станции, различные предприятия и организации сферы обслуживания (магазины, справочные бюро, парикмахерские, билетные кассы, пункты по обмену валюты, ремонтные мастерские, больницы). Такие системы, как компьютерные сети, системы сбора, хранения и обработки информации, транспортные системы, автоматизированные производственные участки, поточные линии, различные военные системы, в частности системы противовоздушной или противоракетной обороны, также могут рассматриваться как своеобразные СМО
Каждая СМО включает в свою структуру некоторое число обслуживающих устройств, которые называют каналами (приборами, линиями) обслуживания. Роль каналов могут играть различные приборы, лица, выполняющие те или иные операции (кассиры, операторы, парикмахеры, продавцы), линии связи, автомашины, краны, ремонтные бригады, железнодорожные пути, бензоколонки и т.д.
Системы массового обслуживания могут быть одноканальными или многоканальными.
Каждая СМО предназначена для обслуживания (выполнения) некоторого потока заявок (требований), поступающих на вход системы большей частью не регулярно, а случайные моменты времени. Обслуживание заявок, в этом случае, также длится не постоянное, заранее известное время, а случайное время, которое зависит от многиx случайных, порой неизвестных нам, причин. После обслуживания заявки канал освобождается и готов к приему следующей заявки. Случайный характер потока заявок и времени их обслуживания приводит к неравномерной загруженности СМО: в иное время на входе СМО могут скапливаться необслуженные заявки, что приводит к перегрузке СМО, а иногда при свободных каналах на входе СМО заявки не будет, что приводит к недогрузке СМО, т.е. к простаиванию ее каналов. Заявки, скапливающиеся на входе СМО, либо «становятся» в очередь, либо по причине невозможности дальнейшего пребывания в очереди покидают СМО необслуженными.
Показатели эффективности функционирования пары «СМО — потребитель», где под потребителем понимают всю совокупность заявок или некий их источник (например, средний доход, приносимый СМО в единицу времени, и т.п.). Эта группа показателей оказывается полезной в тех случаях, когда некоторый доход, получаемый от обслуживания заявок, и затраты на обслуживание измеряются в одних и тех же единицах. Эти показатели обычно носят вполне конкретный характер и определяются спецификой СМО, обслуживаемых заявок и дисциплиной обслуживания.
14. Уравнения динамики для вероятностных состояний (уравнения Колмогорова). Предельные вероятности состояний.
Формально дифференцируя уравнение Колмогорова—Чепмена по s при s = 0 получаем прямое уравнение Колмогорова:
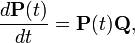
где
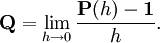
Формально дифференцируя уравнение Колмогорова — Чепмена по t при t = 0 получаем обратное уравнение Колмогорова
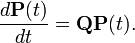
Необходимо подчеркнуть, что для бесконечномерных пространств оператор  уже не обязательно непрерывен, и может быть определен не всюду, например, быть дифференциальным оператором в пространстве распределений. уже не обязательно непрерывен, и может быть определен не всюду, например, быть дифференциальным оператором в пространстве распределений.
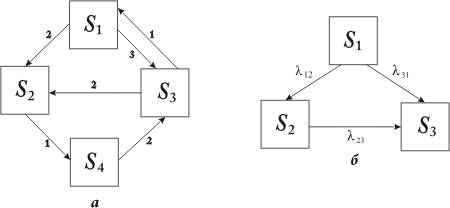
В том случае, если число состояний системы S является конечным и из каждого состояния представляется возможным перейти (за то или иное количество шагов) в каждое другое состояние, то предельные вероятности состояний существуют, а также не зависят от начального состояния системы.
На рис. показаны граф состояния и переходов, удовлетворяющие поставленному условию: из любого состояния система рано или поздно может перейти в любое другое состояние. Условие не будет выполняться при изменении направления стрелки 4—3 на графе рис , а на противоположное.
Допустим, что поставленное условие выполнено, и, следовательно, предельные вероятности существуют:
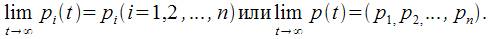
Предельные вероятности будут обозначаться теми же буквами 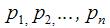 что и вероятности состояний, при этом под ними подразумеваются числа, а не переменные величины (функции времени). что и вероятности состояний, при этом под ними подразумеваются числа, а не переменные величины (функции времени).
Ясно, что предельные вероятности состояний должны давать в сумме единицу: 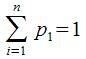 Следовательно, в системе Следовательно, в системе 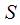 при при 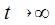 устанавливается некоторый предельный стационарный режим: пусть система и меняет собственные состояния случайным образом, однако вероятность каждого из этих состояний не зависит от времени и каждое из них осуществляется с некоторой постоянной вероятностью, представляющей собой среднее относительное время пребывания системы в этом состоянии. устанавливается некоторый предельный стационарный режим: пусть система и меняет собственные состояния случайным образом, однако вероятность каждого из этих состояний не зависит от времени и каждое из них осуществляется с некоторой постоянной вероятностью, представляющей собой среднее относительное время пребывания системы в этом состоянии.
15. Процесс гибели и размножения.

Марковским процессом гибели и размножения с непрерывным временем назовем такой с.п., который может принимать только целые неотрицательные значения; изменения этого процесса могут происходить в любой момент времени t, при этом в любой момент времени он может либо увеличиваться на единицу, либо остаться неизменным.
Потоками размножения λi(t) будем называть пуассоновские потоки, ведущие к увеличению функции X(t). Соответственно μi(t) – потоки гибели, ведущие к уменьшению функции X(t).
Составим по графу уравнения Колмогорова:

Если поток с конечным числом состояний:

Система уравнений Колмогорова для процесса гибели и размножения с ограниченным числом состояний имеет вид:
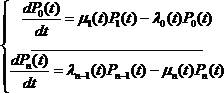
Процессом чистого размножения называется такой процесс гибели и размножения, у которого интенсивности всех потоков гибели равны нулю.

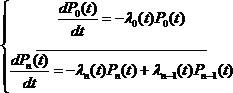
Процессом чистой гибели называется такой процесс гибели и размножения, у которого интенсивности всех потоков размножения равны нулю.
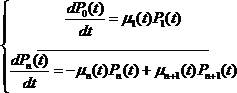
16. Системы массового обслуживания с отказами
.
Наиболее простой из рассматриваемых задач в рамках теории массового обслуживания является модель одноканальной СМО с отказами или потерями.
Следует отметить, что в данном случае количество каналов равно 1 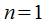 (). Этот канал принимает пуассоновский поток заявок, интенсивность которого равняется (). Этот канал принимает пуассоновский поток заявок, интенсивность которого равняется 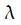 . Время оказывает влияние на интенсивность: . Время оказывает влияние на интенсивность:
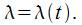
Если заявка прибыла в канал, который в данный момент не является свободным, она получает отказ и больше не числится в системе. Обслуживание заявок осуществляется в течение случайного времени 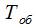 , распределение которого реализуется в соответствии с показательным законом с параметром , распределение которого реализуется в соответствии с показательным законом с параметром 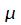 : :
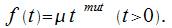
17. Системы массового обслуживания с ожиданием
.
Заявка, поступившая в момент, когда канал занят, становится в очередь и ожидает обслуживания.
Система с ограниченной длиной очереди. Предположим сначала, что количество мест в очереди ограничено числом m, т. е. если заявка пришла в момент, когда в очереди уже стоят m заявок, она покидает систему необслуженной. В дальнейшем, устремив m к бесконечности, мы получим характеристики одноканальной СМО без ограничений длины очереди.
Будем нумеровать состояния СМО по числу заявок, находящихся в системе (как обслуживаемых, так и ожидающих обслуживания):
 —канал свободен; —канал свободен;
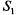 —канал занят, очереди нет; —канал занят, очереди нет;
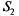 — канал занят, одна заявка стоит в очереди; — канал занят, одна заявка стоит в очереди;
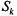 —канал занят, k - 1 заявок стоят в очереди; —канал занят, k - 1 заявок стоят в очереди;
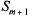 — канал занят, т заявок стоят в очереди. — канал занят, т заявок стоят в очереди.

18. Методы принятия решений в условиях конфликта. Матричные игры. Чистые и смешанные стратегии игр.
Матричная игра – это конечная игра двух игроков с нулевой суммой, в которой задаётся выигрыш игрока 1 в виде матрицы (строка матрицы соответствует номеру применяемой стратегии игрока 2, столбец – номеру применяемой стратегии игрока 2; на пересечении строки и столбца матрицы находится выигрыш игрока 1, соответствующий применяемым стратегиям).
Для матричных игр доказано, что любая из них имеет решение и оно может быть легко найдено путём сведения игры к задаче линейного программирования.
Матричная игра двух игроков с нулевой суммой может рассматриваться как следующая абстрактная игра двух игроков.
Первый игрок имеет m стратегий i = 1,2,...,m, второй имеет n стратегий j = 1,2,...,n. Каждой паре стратегий (i,j) поставлено в соответствие число аij, выражающее выигрыш игрока 1 за счёт игрока 2, если первый игрок примет свою i-ю стратегию, а 2 – свою j-ю стратегию.
Каждый из игроков делает один ход: игрок 1 выбирает свою i-ю стратегию (i=), 2 – свою j-ю стратегию (j=), после чего игрок 1 получает выигрыш аij за счёт игрока 2 (если аij<0, то это значит, что игрок 1 платит второму сумму | аij|). На этом игра заканчивается.
Каждая стратегия игрока i=; j = часто называется чистой стратегией.
Определение. Смешанной стратегией игрока называется полный набор вероятностей применения его чистых стратегий.
Таким образом, если игрок 1 имеет m чистых стратегий 1,2,...,m, то его смешанная стратегия x– это набор чисел x = (x1,..., xm) удовлетворяющих соотношениям
xi³ 0 (i= 1,m), 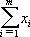 =1. =1.
Аналогично для игрока 2, который имеет n чистых стратегий, смешанная стратегия y– это набор чисел
y = (y1, ..., yn), yj ³ 0, (j = 1,n), 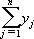 = 1. = 1.
Так как каждый раз применение игроком одной чистой стратегии исключает применение другой, то чистые стратегии являются несовместными событиями. Кроме того, они являются единственными возможными событиями.
Чистая стратегия есть частный случай смешанной стратегии. Действительно, если в смешанной стратегии какая-либо i-я чистая стратегия применяется с вероятностью 1, то все остальные чистые стратегии не применяются. И эта i-я чистая стратегия является частным случаем смешанной стратегии. Для соблюдения секретности каждый игрок применяет свои стратегии независимо от выбора другого игрока.
19. Геометрический метод решения матричной игры.
Решение игр размера 2xn или nx2 допускает наглядную геометрическую интерпретацию. Такие игры можно решать графически.
На плоскости XY по оси абсцисс отложим единичный отрезок A1A2 (рисунок 5.1). Каждой точке отрезка поставим в соответствие некоторую смешанную стратегию U = (u1, u2). Причем расстояние от некоторой промежуточной точки U до правого конца этого отрезка – это вероятность u1 выбора стратегии A1, расстояние до левого конца - вероятность u2 выбора стратегии A2. Точка А1 соответствует чистой стратегии А1, точка А2 – чистой стратегии А2.
В точках А1 и А2 восстановим перпендикуляры и будем откладывать на них выигрыши игроков. На первом перпендикуляре (совпадающем с осью OY) покажем выигрыш игрока А при использовании стратегии А1, на втором – при использовании стратегии A2. Если игрок А применяет стратегию A1, то его выигрыш при стратегии B1 игрока B равен 2, а при стратегии B2 он равен 5. Числам 2 и 5 на оси OY соответствуют точки B1 и B2. Аналогично на втором перпендикуляре найдем точки B'1 и B'2 (выигрыши 6 и 4).
Соединяя между собой точки B1 и B'1, B2 и B'2, получим две прямые, расстояние от которых до оси OX определяет средний выигрыш при любом сочетании соответствующих стратегий.
Например, расстояние от любой точки отрезка B1B'1 до оси OX определяет средний выигрыш игрока A при любом сочетании стратегий A1 и A2 (с вероятностями u1 и u2) и стратегии B1 игрока B.
Ординаты точек, принадлежащих ломаной B1MB'2 определяют минимальный выигрыш игрока A при использовании им любых смешанных стратегий. Эта минимальная величина является наибольшей в точке М, следовательно, этой точке соответствует оптимальная стратегия U* = (, ), а ее ордината равна цене игры v.
Координаты точки M найдем, как координаты точки пересечения прямых B1B'1 и B2B'2.
Для этого необходимо знать уравнения прямых. Составить такие уравнения можно, используя формулу для уравнения прямой, проходящей через две точки:

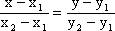
Составим уравнения прямых для нашей задачи.
Прямая B1B'1: 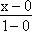 = = 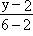 или y = 4x + 2. или y = 4x + 2.
Прямая B2B'2: 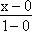 = = 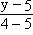 или y = -x + 5. или y = -x + 5.
Получим систему: y = 4x + 2,
y = -x + 5.
Решим ее: 4x + 2 = -x + 5,
5x = 3,
x = 3/5, y = -3/5 + 5 = 22/5.
Таким образом, U = (2/5, 3/5), v = 22/5.
20. Биматричные игры.
Биматричная игра – это конечная игра двух игроков с ненулевой суммой, в которой выигрыши каждого игрока задаются матрицами отдельно для соответствующего игрока (в каждой матрице строка соответствует стратегии игрока 1, столбец – стратегии игрока 2, на пересечении строки и столбца в первой матрице находится выигрыш игрока 1, во второй матрице – выигрыш игрока 2.)
Для биматричных игр также разработана теория оптимального поведения игроков, однако решать такие игры сложнее, чем обычные матричные.
21. Статистические игры. Принципы и критерии принятия решений в условиях полной и частичной неопределенности.
В исследовании операций принято различать три типа неопределенностей :
неопределенность целей;
неопределенность наших знаний об окружающей обстановке и действующих в данном явлении факторах (неопределенность природы);
неопределенность действий активного или пассивного партнера или противника.
В приведенной выше классификации тип неопределенностей рассматривается с позиций того или иного элемента математической модели. Так, например, неопределенность целей отражается при постановке задачи на выборе либо отдельных критериев, либо всего вектора полезного эффекта.
С другой стороны, два другие типа неопределенностей влияют, в основном, на составление целевой функции уравнений ограничений и метода принятия решения. Конечно, приведенное выше утверждение является достаточно условным, как, впрочем, и любая классификация. Мы приводим его лишь с целью выделить еще некоторые особенности неопределенностей, которые надо иметь в виду в процессе принятия решений.
Дело в том, что кроме рассмотренной выше классификации неопределенностей надо учитывать их тип (или "род") с точки зрения отношения к случайности.
о этому признаку можно различать стохастическую (вероятностную) неопределенность, когда неизвестные факторы статистически устойчивы и поэтому представляют собой обычные объекты теории вероятностей - случайные величины (или случайные функции, события и т.д.). При этом должны быть известны или определены при постановке задачи все необходимые статистический характеристики (законы распределения и их параметры).
Примером таких задач могут быть, в частности, система технического обслуживания и ремонта любого вида техники, система организации рубок ухода и т.д.
Другим крайним случаем может быть неопределенность нестохастического вида (по выражению Е.С.Вентцель - "дурная неопределенность"), при которой никаких предположений о стохастической устойчивости не существует. Наконец, можно говорить о промежуточном типе неопределенности, когда решение принимается на основании каких-либо гипотез о законах распределения случайных величин. При этом ЛПР должен иметь в виду опасность несовпадения его результатов с реальными условиями. Эта опасность несовпадения формализуется с помощью коэффициентов риска.
Принятие решений в условиях риска может быть основано на одном из следующих критериев:
критерий ожидаемого значения;
комбинации ожидаемого значения и дисперсии;
известного предельного уровня;
наиболее вероятного события в будущем.
|