Учреждение образования «Брестский государственный университет
имени А.С.Пушкина»
Физический факультет
Кафедра теоретической физики и астрономии
Реферат по специализации
«Теоретическая физика»
Уравнение состояния сверхплотного вещества.
Брест 2010
Уравнение состояния для Ае- и Аеп-фаз вещества
Мы будем иметь дело с моделями звездных конфигураций, состоящих из вырожденных газовых масс. Это конфигурации белых карликов и барионных звезд. Под последними подразумеваются модели небесных тел, состоящих из вырожденного барионного газа. В расчетах параметров этих звездных конфигураций нужно иметь уравнение состояния вещества. Нас интересуют только вырожденные состояния вещества.
Начнем с рассмотрения Ае-фазы. Она состоит из голых атомных ядер и свободного вырожденного электронного газа. При достаточно низких температурах движение ядер сводится лишь к тому, что они совершают нулевые колебания около фиксированных точек равновесия. Поэтому они не дают никакого вклада в давление вещества. Давление целиком обусловлено электронами, плотность же энергии определяется атомными ядрами.
Плотность энергии равна
ρ = (тп
с2
+b)∑ 2 Ак
пк
+ 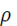 e
(1) e
(1)
где b— средняя энергия связи нуклона в ядрах (здесь нет смысла различать массы протона и нейтрона), пк
— число ядер данного типа (с параметрами Ак
и Zк
) в единице объема, ρе
— плотность энергии электронного газа. В условиях наличия вырожденного электронного газа bявляется функцией 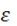 е
.Согласно е
.Согласно
ρе
= 4Ке(хе
(1 + 2х2
e
)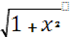 - -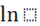 (хе
+ (хе
+ 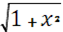 )) (2) )) (2)
где, хе
= ρе
/mе
с = (3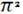 )1
/3
hne
1/3
me
с — граничный импульс электронов в единицах mе
с (при ре
>> те
с, хе
= )1
/3
hne
1/3
me
с — граничный импульс электронов в единицах mе
с (при ре
>> те
с, хе
= 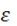 е
/те
с2
) и е
/те
с2
) и
Ке 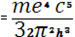 (3) (3)
Иногда удобно взамен хe
использовать параметр tе
:
tе
=4arshxe
(4)
С помощью этого параметра плотность энергии электронов запишется в следующем компактном виде:
ρe
= Ке(sh te
- te
). (5)
В выражении энергии (1) можно произвести некоторые упрощения. Так,
∑Ak
nk
= ∑Zk
nk
= ∑Zk
nk
= ne ne
где А/Zесть средняя величина отношения Ак
/Zк
(усредненная по всем типам ядер, имеющихся в среде). Учитывая последнее и пренебрегая малыми величинами bи ρе
, получаем
ρ=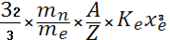 (6) (6)
Напомним, что из-за явления нейтронизации отношение А/ Zявляется функцией хе
, эта зависимость аппроксимирована полиномом. Теперь вычислим давление. Оно равно производной энергии по объему с обратным знаком, при постоянном числе частиц и энтропии (в данном случае энтропия равна нулю). Так как парциальное давление ядер не учитывается, то
Реклама

P=-(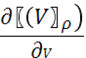 )Ne
=-( )Ne
=-(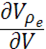 )Ne )Ne
где Nе
= Vпе
— число электронов в некотором объеме V. При дифференцировании ρе
нужно учесть, что хе
зависит от объема V. Имея в виду (2), находим для давления
Р =  Ке [xе
(2 Ке [xе
(2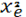 - 3) - 3) 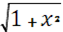 +3 +3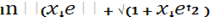 ].(7) ].(7)
Учитывая также формулу, уравнение состояния вещества в Aе-фазе можно записать в следующем параметрическом виде:
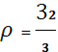 ( (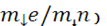 3
Kn 3
Kn
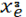 (2+a1
xe
+a2 (2+a1
xe
+a2
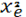 +a3 +a3
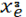 , ,
P=(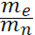 )4
K(8) )4
K(8)
Где a1,
a2
, а3
— постоянные, входящие в формулу: а1
= 1,255 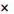 10-2
, а2
=1,755 10-2
, а2
=1,755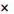 10-5
, а3
=1,376 10-5
, а3
=1,376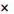 10-6
; кроме того, мы ввели также новое обозначение 10-6
; кроме того, мы ввели также новое обозначение
Кп
= 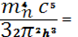 5,11 5,11 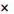 1035
эрг 1035
эрг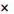 см-3
, (9) см-3
, (9)
которое будет встречаться в дальнейшем.
Рассмотрим два важных предельных случая уравнения состояния (8). В нерелятивистском случае параметр хе
мал по сравнению с единицей. Разложим Р в ряд по степеням хе
и отбросим малые величины в выражениях ρ и Р; исключая параметр х, получим
Р=Aρ5/3
, (10)
Где
A= )5/3
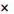 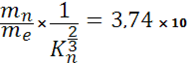 -23
)5/3 -23
)5/3
Величина η= A/Z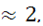 для всех ядер, за исключением водорода. для всех ядер, за исключением водорода.
Р=Bρ4/3
, (11)
Где
B=5,64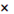 10-14
)4/3 10-14
)4/3
В выражении для плотности энергии мы опустили bи ρе
.
Энергия связи нуклона в ядре имеет значение в интервале 0<b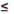 8 Мэв. У порога исчезновения Aе-фазы Р 8 Мэв. У порога исчезновения Aе-фазы Р 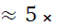 1029
эрг 1029
эрг см-3
, а отношение парциальных плотностей энергии электронов и ядер порядка см-3
, а отношение парциальных плотностей энергии электронов и ядер порядка
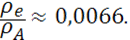
Таким образом, bи ρе
действительно достаточно малы и в расчетах звездных конфигураций не могут играть сколько-нибудь заметную роль.
В приведенном уравнении состояния не учтено взаимодействие частиц. Здесь мы имеем дело только с кулоновскими силами . Было показано, что потенциальная энергия электрона, обусловленная электрическими силами, мала по сравнению с его кинетической энергией, причем с возрастанием плотности отношение их уменьшается. Таким образом, приближение идеального газа здесь вполне оправдано. Ряд поправок к выражению давления (8), обусловленных кулоновскими взаимодействиями. Поправки к Р некоторую роль могут играть лишь при больших Zи х<1. Изменения, обусловленные температурой, тоже несущественны. Здесь важным является эффект зависимости А/Zот граничной энергии электронов.
Уравнение состояния (8) применимо до x=46, чему соответствует плотность ρ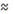 2,4 2,4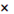 1032
эрг 1032
эрг см-3
. При больших плотностях мы имеем дело с Aen-фазой, где уравнение состояния другое. см-3
. При больших плотностях мы имеем дело с Aen-фазой, где уравнение состояния другое.
Реклама

Введем параметр
tn
=4arshxn
,
тогда ρп
и Рп
запишутся в следующем виде:
ρn
=Kn
(sh tn
- tn
),
Pn
= Kn
(sh tn
- 8sh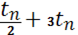 ).(13) ).(13)
Учитывая также энергию атомных ядер, парциальное давление и плотность энергии электронов, для уравнения состояния Aen-фазы вещества получаем
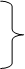 ρ=Kn
(sh tn
- tn
)+mn
c2 ρ=Kn
(sh tn
- tn
)+mn
c2
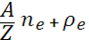 , ,
P= Kn
(sh tn
- 8sh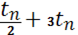 )+Pe
.(14) )+Pe
.(14)
Здесь ρе
и Рe
—плотность энергии и давление электронного газа. Заметим, что чуть выше порога появления Aen-фазы парциальная плотность энергии и давление электронов (можно даже сказать — плотность энергии атомных ядер) достаточно малы по сравнению с соответствующими величинами для нейтронного газа. Здесь почти на всем протяжении фазы энергия и давление системы в основном определяются нейтронным газом.
Вообще говоря, в Aen-фазе следовало бы учитывать ядерные взаимодействия между нейтронами. Их вклад несуществен для энергии, но, по-видимому, является важным для давления: при заданном числе нейтронов учет ядерных сил приведет к уменьшению давления. Насколько нам известно, в рассматриваемой области плотностей теория ядерной материи как следует не разработана, поэтому мы довольствуемся приближением идеального газа. Уравнение состояния (14) справедливо в области плотностей 2,4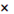 1032 1032
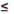 ρ ρ 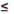 5.45 5.45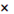 1034
эрг 1034
эрг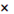 см-3
. см-3
.
Об асимптотическом виде уравнения состояния
Целесообразно сначала исследовать асимптотическое поведение вида уравнения состояния при чрезвычайно больших плотностях. Здесь можно достичь определенного результата, исходя из совершенно общих соображений. В опытах по рассеянию быстрых протонов на нуклонах было установлено наличие весьма интенсивных сил отталкивания, действующих на расстояниях r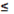 2 2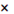 10-14
см. Этот экспериментальный факт дает некоторое основание утверждать, что в надъядерной области с возрастанием плотности массы состояние барионной плазмы (мы говорим о барионной плазме, поскольку концентрация лептонов в ней очень мала) все больше отходит от газа и постепенно приближается к состоянию идеальной жидкости. 10-14
см. Этот экспериментальный факт дает некоторое основание утверждать, что в надъядерной области с возрастанием плотности массы состояние барионной плазмы (мы говорим о барионной плазме, поскольку концентрация лептонов в ней очень мала) все больше отходит от газа и постепенно приближается к состоянию идеальной жидкости.
Можно доказать, что при любом типе взаимодействия, если только энергия взаимодействия частиц больше их кинетической, известный закон Р 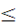 ρ/3 обязательно нарушается, т. е. давление при достаточно больших плотностях может иметь значения выше ρ/3. Соотношение ЗР ρ/3 обязательно нарушается, т. е. давление при достаточно больших плотностях может иметь значения выше ρ/3. Соотношение ЗР 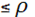 имеет место для идеального газа и в тех случаях, когда поля настолько слабы, что при любых плотностях кинетическая энергия частиц всегда больше их энергии взаимодействия. Такими полями являются электромагнитное, гравитационнное и некоторые типы мезонных полей. имеет место для идеального газа и в тех случаях, когда поля настолько слабы, что при любых плотностях кинетическая энергия частиц всегда больше их энергии взаимодействия. Такими полями являются электромагнитное, гравитационнное и некоторые типы мезонных полей.
Литература
1. Саакян, Г.С. Равновесные конфигурации вырожденных газовых масс / Г.С. Cаакян.-М.: Наука, 1972.
2. Секержицкий, В.С., Секержицкий, С.С. К вопросу о параметрах холодного сверхплотного вещества с учетом плотности ядер//К 100-летию со дня рождения Гейзенберга. – 2001, БрГУ.
|