| ˛˜¯—˘ ˝¨¯
6 ª º ß 3
6.1 ˚ º ª º . . . . . . . . . . . . . . . . . . . . . . 3
6.2 º ŁŁ æ æ Œ . ` . ı ˆ 6
6.3 ˜ ºŁ æ ª º . ˝˛˜ Ł ˝˛˚ . . . . . . . . . . . . 9
6.4 ˝ Ł Ł æ . ˚ Ł æŒ º Ł . ˚ æ . . 20
6.5 ˇ Ł Ł Œ æ . . . . . . . . . . . . . . . . . . . 26
6.6 ºª Æ Ł æŒŁ Œ ß º . . . . . . . . . . . . . . . . 28
6.7 ª º ß Łæº ß Ł º Ł . . . . . . . . . . . . . 32
7 ˛æ ß ºª Æ Ł æŒŁ æ Œ ß 36
8 ¸Ł Ø ß æ æ 37
8.1 ˇ Ł ºŁ Ø ª æ æ . . . . . . . . . . . . . . . 37
8.2 ` Łæ ºŁ Ø ª æ æ . . . . . . . . . . . . . . . . 39
8.3 ¨ Ł ºŁ Ø ßı æ æ . . . . . . . . . . . . . 43
8.4 ˇ ı ª Æ Łæ Œ ª . Ł ı . . 47
8.5 ¸Ł Ø ß æ æ . . . . . . . . . . . . . . . . . . 50
9 ¸Ł Ø ß ß ºŁ Ø æ æ 58
9.1 ˇ æ æ Ł ºª Æ ºŁ Ø ßı . . . . . . . 58
9.2 Ł ºŁ Ø ª Œ ºŁ Ø
æ æ . . . . . . . . . . . . . . . . . . . . . . . . . . 62
9.3 — ª Ł Œ ºŁ Ø ª . . . . . . . . . . . . . 68
9.4 ˛Æ Ł æ ºŁ Ø ª . . . . . . . . . . . . . . 71
1
2 ˛˜¯—˘ ˝¨¯
9.5 Œ Łæ Ł æŒŁØ ª º Ł ß Ł ºŁ Ø ª -
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72
9.6 Ææ ß Œ ß Ł æ Ææ ß Ł ºŁ Ø ª
Реклама

Ł Ł ß . . . . . . . . . . . . . . . . . . . . . 76
ˆº 6
ª º ß
6.1 ˚ º ª º
ˇ æ k
Œ ŁŒæŁ º .
˛ º Ł 6.1.1. ª º Ł æ ª x
Œ º k
ß æ º ß Ł Ł
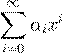 , ,
ª x
æŁ º Ł æ ª , αi
º ß º k
, Ł æ ß
0, æ (∃ n
∈ N) (∀ i > n
) αi
= 0.
´ º Øł ª º ß Æ Æ f
(x
), g
(x
), h
(x
), f
1
(x
), f
2
(x
),...ŁºŁ Œ f
, g
, h
, f
1
, f
2
,...
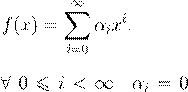 (6.1) (6.1)
¯æºŁ ª º (6.1), ª º Æ ß º ß Ł Æ 0.
˛ º Ł 6.1.2. º ª ß αi
x
i
Æ ß º Ł ª -
º (6.1), º ß αi
Æ ß Œ Ł Ł Ł ª º
(6.1).
3
¯æºŁ ª º (6.1) ∀ i > n αi
= 0, Æ Łæ :
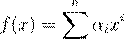 ŁºŁ f
(x
) = α
0
+ α
1
x
+ ··· + αn
xn
.
(6.2) ŁºŁ f
(x
) = α
0
+ α
1
x
+ ··· + αn
xn
.
(6.2)
i
=0
˙ æ Ł ı ŁæŁ (6.1) Œ ŁæŁ (6.2) ß Łł α
0
æ α
0
x
0
.
ˇ Ł α
0
ß æ æ Æ ß º ª º f
(x
).
˛ º Ł 6.1.3. º ª ª º f
(x
)
ß æ ŁÆ º łŁØ ºŁ ª º Œ Ł Ł ª ª º .
˛Æ Ł degf
(x
) æ ª º f
(x
).
¯æºŁ ŁæŁ (6.2) αn
6= 0, æ ª º f
(x
) n
, æ degf
(x
) = n
. ´ æº , αn
xn
ß æ æ łŁ º
ª º , αn
ß æ æ łŁ Œ Ł Ł ª º .
æ æ ı ª º Ł æ ª x
º k
Æ -
æ k
[x
]
Ł ß æ Œ º ª º º k
.
ˇ æ
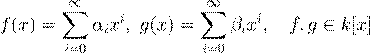 . .
˛ º Ł 6.1.4. ˜ ª º f
(x
),g
(x
) ∈ k
[x
] ß æ ß Ł, æºŁ ß æ Łı Œ Ł Ł ß Ł Ł Œ ßı æ ı x
,
Реклама

æ (∀ 0 6 i <
∞) αi
= βi
.
´ æ k
[x
]
ŁŁ: æº Ł Ł Ł -
ª º .
˛ º Ł 6.1.5. Ø ı ª º f
Ł g
ß æ -
ª º
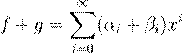 . .
ˇ Ł Ł ı ª º f
Ł g
ß æ ª º
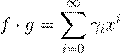 ,
ª γ
i
= X α
ν
β
µ
. ,
ª γ
i
= X α
ν
β
µ
.
νν,µ
+µ
>=0i
6.1. ˚ º ª º
˙ Ł
6.1.1.
º º Ł , º ª , Æß
Ł ª º , æ Œ ßØ º ª ª º Ł Œ ßØ º ª ª º Ł Ł æ Ł Æß º ß.
˛ º Ł 6.1.5 Œ Œ æ ßæº , f
+ g
Ł f
· g
Øæ Łº Æ ª º Ł. Œ Œ Œ f
Ł g
ª º ß, (∃ n
∈
∈ N) (∀ i > n
) αi
= 0, βi
= 0. ª (∀ i > n
) αi
+ βi
= 0 ⇒ f
+ g
º æ ª º .
˜º f
· g
æ Ł γi
,
∀ i >
2n
. ΠΠΠi
= ν
+ µ
, Ł æº Ł
i >
2n
⇒ ν > n
ŁºŁ µ > n
⇒ αν
= 0 ŁºŁ βµ
= 0 ⇒ γi
= P
αν
βµ
= 0 º i >
2n
. , f
· g
º æ ª º . — ææ Ł æ æ Ł æ ß Ł Ł Ł ı ª º .
ˇ æ f
6= 0 Ł g
6= 0 ª º ß Ł k
[x
],
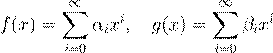 . .
ˇ æ degf
= n
, æ αn
6= 0,
degg
= m
, æ βm
6= 0. ˛Æ Ł
N
= max(n,m
).
— ææ Ł
æ , 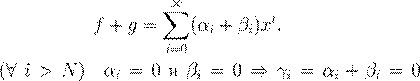 . º - . º -
 º , deg(f
+ g
) 6 N
. ˙ Ł , deg(f
+ g
) 6 max(degf,
degg
). ˙ Œ º , deg(f
+ g
) 6 N
. ˙ Ł , deg(f
+ g
) 6 max(degf,
degg
). ˙ Œ
æ æ Łª æ , Ł , Ł n
6= m
.
— ææ Ł
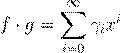 ª γ
i
= X α
ν
β
µ
. ª γ
i
= X α
ν
β
µ
.
νν,µ
+µ
>=0i
¯æºŁ i > n
+ m
, ν > n
ŁºŁ µ > m
⇒ αν
= 0 ŁºŁ βµ
= 0 ⇒ γi
= 0.
ˇ º degf
· g
6 n
+ m
. ˙ Ł , degf
· g
6 degf
+ degg
.
æ Ł
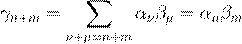 . .
Œ Œ Œ αn
6= 0 Ł βm
6= 0, αn
βm
6= 0.
´ æº γn
+m
6= 0 Ł
 degf
· g
= degf
+ degg
. degf
· g
= degf
+ degg
.
6.2 º ŁŁ æ æ Œ . ` . ı ˆ
¯˛—¯ 6.2.1 ( º ŁŁ æ æ Œ ). ˇ æ k
º , f
Ł g
∈ k
[x
], Ł g
6= 0. ª æ ø æ Ł æ ª -
º q,r
∈ k
[x
] Π,
1) f
= gq
+ r
;
2) r
= 0 (ŁºŁ r
6= 0,
degr <
degg
).
˜ Œ º æ . I) ø æ Ł ª º q
Ł r
.
) ˇ æ f
= 0 (ŁºŁ f
6= 0,
degf <
degg
). ´ æº Łæ f
= 0 · g
+ f,
(q
= 0, r
= f
). æº Ł 1) Ł 2) ß º ß.
Æ) f
6= 0 Ł degf
> degg
. ˇ æ
f
= αn
xn
+ ...
+ α
0
, αn
6= 0, g
= βm
xm
+ ...
+ β
0
, βm
6= 0.
degf
= n,
degg
= m, n
> m
. ˇ æ Ł ª º
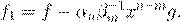 (1) (1)
| ª º f
1
æ Œ, Æß Ł Ł
f
. ¨ f
1
= 0 ŁºŁ f
1
6= 0 Ł degf
1
= n
1
< n
.
|
æ
|
łŁØ º
|
ª
|
º
|
| ¯æºŁ n
1
< m
, ææ æ Ł ª
|
º
|
Œ
|
Ł
|
. ¯æ-
|
ºŁ n
1
> m
, , Æ 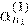 æ łŁØ Œ Ł Ł f
1
, æ Ł æ łŁØ Œ Ł Ł f
1
, æ Ł
ª º
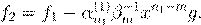 (2) (2)
6.2. º ŁŁ æ æ Œ . ` . ı ˆ ˛ ª º f
2
æ Ł æ ŒŁ Æ , Æß Ł Ł æ -
łŁØ º ª º f
1
. ¨ f
2
= 0 ŁºŁ f
2
6= 0 Ł degf
2
= n
2
< n
1
.
¯æºŁ n
2
< m
, ææ æ Ł ª º Œ Ł . ¯æºŁ n
2
> m
, º Ł . .
˙ Ł , æ Ł ª º f
, f
1
, f
2
, f
3
,... Æ æ ª
Æß ø æº º æ º ßı Łæ º, ª Œ Œ -
º Ł n > n
1
> n
2
> ... > ns
, ª ns
< m
.
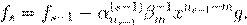 (s
) (s
)
ª fs
= 0 ŁºŁ fs
6= 0 Ł degfs
= ns
< m
.
º Ł º æ æ (1),
(2),...,
(s
), º Ł
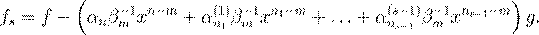
˛Æ Ł fs
r
, æ Ł æŒ ÆŒŁ q
. ˇ º Ł r
= f
s
−
  − qg
⇒ f
= qg
+ r
, æ º ŁºŁ æ 1), ª r
= 0 ∨ (r
6= − qg
⇒ f
= qg
+ r
, æ º ŁºŁ æ 1), ª r
= 0 ∨ (r
6=
 6= 0 ∧ degr <
degg
) æº Ł 2). 6= 0 ∧ degr <
degg
) æº Ł 2).
II) ¯ Ł æ æ q
Ł r
.
 ˜ æ Ł , æ Ø ª º q
Ł r
, æ º ßı æ Ł I), æ ø æ ª ª º q
Ł r
, º ø ˜ æ Ł , æ Ø ª º q
Ł r
, æ º ßı æ Ł I), æ ø æ ª ª º q
Ł r
, º ø
  æº Ł 1) Ł 2), æ f
= qg
+ r
Ł r
= 0 ∨ (r
= 06 ∧ degr <
degg
). æº Ł 1) Ł 2), æ f
= qg
+ r
Ł r
= 0 ∨ (r
= 06 ∧ degr <
degg
).
¨
     qg
+ r
= qg
+ r
⇒ (q
− q
)g
= r
− r.
(∗) ˇ Œ , q
− q
= 0. ˜ æ Ł Ł , æ q
− q
6= 0. ˇ æ α
6= 0
æ łŁØ Œ Ł Ł ª ª º , ª æ łŁØ Œ - qg
+ r
= qg
+ r
⇒ (q
− q
)g
= r
− r.
(∗) ˇ Œ , q
− q
= 0. ˜ æ Ł Ł , æ q
− q
6= 0. ˇ æ α
6= 0
æ łŁØ Œ Ł Ł ª ª º , ª æ łŁØ Œ -
 Ł Ł ª º (q
−q
)g
Æ αβm
6= 0. ¯æºŁ Æß αβm
= 0, α
= 0. Ł Ł ª º (q
−q
)g
Æ αβm
6= 0. ¯æºŁ Æß αβm
= 0, α
= 0.
  ˙ Ł deg(q
− q
)g
= deg(q
− q
) + degg
> degg
. ˙ Ł deg(q
− q
)g
= deg(q
− q
) + degg
> degg
.
   ª Ø æ ß r
− r
= 0 ŁºŁ r
− r
6= 0,
deg(r
− r
) <
degg
. ß ª Ø æ ß r
− r
= 0 ŁºŁ r
− r
6= 0,
deg(r
− r
) <
degg
. ß
º ŁºŁ, æ (∗)
æº æ Ł ª º , æ Œ ª ł degg
, æ æ Ł º Ø ª º ŁºŁ ª º , æ Œ ª ł degg
. Ł æ Ł Ł .  ˛ º Ł 6.2.1. ´ Æ Ł ı ß 6.2.1 ª º ß q
Ł r
ß æ æ æ º ß æ ß Ł æ Œ º Ł ˛ º Ł 6.2.1. ´ Æ Ł ı ß 6.2.1 ª º ß q
Ł r
ß æ æ æ º ß æ ß Ł æ Œ º Ł
ª º f
ª º g
.
¯˛—¯ 6.2.2 (` ). ˛æ Œ º Ł ª º f
(x
)
x
− γ
Ł ª º f
(x
) Ł x
= γ
, æ f
(γ
).
˜ Œ º æ . ˇ æ f
(x
) = q
(x
)(x
− γ
) + r
(x
), r
(x
) = 0 ∨ (r
(x
) 6= 6= 0 ∧ degr
(x
) <
1). ˇ º r
(x
) = 0 ∨ degr
(x
) = 0, º Æ æº
r
(x
) = r
∈ k
.
ˇ æ q
(x
) = β
0
+β
1
x
+...
+βs
xs
, ª f
(x
) = q
(x
)·x
−q
(x
)γ
+r
=
= β
0
x
+ β
1
x
2
+ ...
+ βs
xs
+1
− β
0
γ
− β
1
xγ
− ...
− βs
xs
γ
+ r
.
æ Ł f
(γ
) = β
0
γ
+β
1
γ
2
+...
+βs
γs
+1
−β
0
γ
−β
1
γ
2
−...
+βs
γs
+1
+r
=
= r
. ŒŁ Æ , r
= f
(γ
). 
ˇ æ º Ł æ º Ł ª º f
(x
) (x
− γ
) Œ ß Ø æı ˆ .
ˇ æ f
(x
) = α
0
xn
+ α
1
xn
−1
+ ...
+ αn
,α
0
6= 0. — ºŁ f
(x
)
(x
− γ
) æ æ Œ , º Ł f
(x
) = q
(x
)(x
− γ
) + r
. ª º q
(x
)
Æ ŁæŒ Ł q
(x
) = β
0
xn
−1
+ β
1
xn
−2
+ ...
+ βn
−1
. ˝ ł Ø Ł Œ Ł Ł ß β
0
,β
1
,...,βn
−1
Ł æ Œ r
.
ˇ æ Ł æ ł Ł æ q
(x
)
Ł f
(x
)
Łı Ł . ¨ , 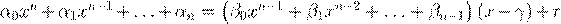 . ˜ . ˜
| ª º
|
ß ª Ł º Œ ª
|
, Œ ª ß Łı Œ Ł Ł
|
ß
|
| Ł æ
|
æ øŁı æ ı.
|
Ł Œ Ł Ł ß.
|
| x
n
: α
0 = β
0
|
⇒ β
0
= α
0
;
|
| x
n
−1 : α
1 = β
1 − β
0γ
|
⇒ β
1
= β
0
γ
+ α
1
;
|
| x
n
−2 : α
2 = β
2 − β
1γ
...
|
⇒ β
2
= β
1
γ
+ α
2
;
|
| x
1 : α
n
−1 = β
n
−1 − β
n
−2γ
|
⇒ β
n
−1 = β
n
−2γ
+ α
n
−1;
|
| x
0 : α
n
= r
− β
n
−1γ
|
⇒ r
= βn
−1
γ
+ αn
.
|
ŒŁ Æ Ł , Œ Ł Ł ß º ª æ ª Ł æ -
Œ ı æ æ ø Ł ßı ß Łæº ŁØ, Ł , Æß Ø-
Ł βk
= βk
−1
γ
+αk
. Ł ß Łæº Ł Æ Łæß Ł æº ø Ø æı ß ˆ .
| α
0
|
α
1
|
α
2
|
...
|
α
n
−1
|
αn
|
| γ
|
α
0
|
β
0
γ
+ α
1
|
β
1
γ
+ α
2
|
...
|
βn
−2γ
+ αn
−1
|
β
n
−1γ
+ α
n
|
| ||
|
||
|
||
|
||
|
||
|
| β
0
|
β
1
|
β
2
|
...
|
β
n
−1
|
r
= f
(γ
)
|
ˇ Ł
: f
(x
) = x
5
− 2x
4
+ 3x
3
− 4x
2
+ x
− 1. ˝ Ø f
(4).
| 1
|
−2
|
3
|
−4
|
1
|
−1
|
| 4
|
1
|
2
|
11
|
40
|
161
|
643
|
f
(4) = 643, f
(x
) = (x
4
+ 2x
3
+ 11x
2
+ 40x
+ 161)(x
− 4) + 643.
6.3 ˜ ºŁ æ ª º . ˝ ŁÆ º łŁØ ÆøŁØ ºŁ º Ł Ł ł Æø Œ
˛ º Ł 6.3.1. ˆ , ª º f
(x
)
ºŁ æ ª -
º g
(x
) 6= 0 ŁºŁ, ª º g
(x
) ºŁ ª º f
(x
) ŁºŁ,
ª º g
(x
)
º æ ºŁ º ª º f
(x
)
ŁºŁ, ª º f
(x
)
Œ ª º g
(x
)
, æºŁ æ ø æ Œ Ø ª º q
(x
)
,
f
(x
) = q
(x
) · g
(x
).
˛ º Ł 6.3.2. ˆ , ª º f
(x
)
ºŁ æ ª º
g
(x
) 6= 0, æºŁ æ Œ º Ł f
(x
) g
(x
) º .
, ª º g
(x
) ºŁ f
(x
) Æ æ Œ Œ g
|f
.
˛ º Ł 6.3.3. ˜ º ßı ª º f
(x
)
Ł g
(x
)
ß æ ææ ŁŁ ß Ł f
∼ g
, æºŁ Ł ºŁ æ ª ª Ł º ß º Ø Œ æ , æ f
= αg
, α
∈ k
∗
= k
\{0}.
Øæ ºŁ æ Ł
1. (∀ f
6= 0) f
|f
.
2. (∀ g
6= 0) g
|0.
3. ˜ º ßı ª º ææ ŁŁ ß ª Ł º Œ ª ,
| Œ ª Ł º
|
ª ª , æ f
∼ g
⇔ f
|g
Ł g
|f
.
|
| 4. ¯æºŁ h
|g
, g
|f
,
|
h
|f
( Ł Ł æ ).
|
| 5. ¯æºŁ h
|g
, h
|f
,
|
(∀ u,v
∈ k
[x
]) h
|(ug
+ vf
).
|
| 6. ˜ ºŁ º Ł
|
º ßı Œ æ ª Æß º Œ
|
º
|
ß Œ
|
-
|
æ ß, æ æºŁ g
|f
Ł degf
= 0, degg
= 0.
7. ˝ º Œ æ ºŁ º Ø ª º , æ æºŁ
degg
= 0, (∀ f
) g
|f
.
8. ¯æºŁ g
|f
Ł f
6= 0, degg
6 degf
, Ł Œ æ æ Łª æ ª Ł º Œ ª , Œ ª g
∼ f
.
9. ˛ ł Ł ºŁ æ Ł, æ ł Ł Œº ææ Ł ææ ŁŁ -
ßı ª º , æ æºŁ g
|f
, g
1
∼ g
, f
1
∼ f
, g
1
|f
1
.
˜ Œ º æ . 1) f
(x
) = 1 · f
(x
), æ f
|f
Ł q
(x
) = 1.
2) 0 = 0 · g
(x
), æ g
|0 Ł q
(x
) = 0.
3) ) ˝ Æı Ł æ .
ˇ æ f
∼ g
, ª f
= αg
, ª α
∈ k
∗
, æ g
|f
Ł q
= α
. Œ Œ Œ
α
6= 0, g
= α
−1
f
, æ f
|g
Ł q
= α
−1
.
b) ˜ æ æ .
ˇ æ g
|f
Ł f
|g
. ¨ , f
= qg
, g
= q
1
f
, æº º f
= q
(q
1
f
), æ (1−qq
1
)f
= 0. ΠΠΠf
6= 0, 1−qq
1
= 0, æ qq
1
= 1. ˙ Ł degqq
1
= 0 ⇒ degq
+ degq
1
= 0 ⇒ degq
= degq
1
= 0, æº º q
Ł q
1
Œ æ ß. ¨ f
= qg
, ª q
∈ k
∗
⇒ f
∼ g
.
4) ¨ g
= qh, f
= q
1
g
. ª f
= q
1
(qh
) = (q
1
q
)h
⇒ h
|f
.
5) ¨ g
= qh
, f
= q
1
h
. ª ug
= uqh
, vf
= vq
1
h
. — ææ Ł
ug
+ vf
= (uq
+ vq
1
)h
⇒ h
|(ug
+ vf
).
6) ¨ degf
= 0 Ł f
= qg
⇒ degf
= degq
+ degg
= 0 ⇒ degq
= = degg
= 0, æ q
Ł g
Œ æ ß.
7) ΠΠΠdegg
= 0, g
∈ k
∗
, æ ø æ g
−1
∈ k
∗
. ª
f
= (fg
−1
)g
⇒ g
|f
.
8) ¨ f
= qg
⇒ degf
= degg
+ degq
⇒ degf
> degg
. ´Ł ,
| Œ æ Æ ß º æ ª
= 0 ⇒ q
∈ k
∗
⇔ f
∼ g
.
|
Ł º Œ ª
|
, Œ ª degq
=
|
| 9) ¨ f
= qg
, g
= αq
1
, f
= βf
1
, ª
|
α,β
∈ k
∗
. ª
|
βf
1
= qαg
1
⇒
|
⇒ f
1
= (β
−1
qα
)g
1
⇒ g
1
|f
1
. 
| ´ º Øł Æ ææ Ł Œ
|
æŁæ ª
|
º
|
| {f
1
,f
2
,...,fs
}, æ Ł Œ ßı Œ Ø Ø
º .
|
Ł ª º
|
ºŁ
|
| ˛ º Ł 6.3.4. ª º d
ß
|
æ
|
ÆøŁ ºŁ º
|
æŁæ -
|
| ß ª º {f
1
,f
2
,...,fs
}, æºŁ æŁæ ß, æ (∀ 1 6 i
6 s
) d
|fi
.
|
ºŁ
|
æ ª º ß
|
Ø
|
| ¯˛—¯ 6.3.1 ( æŁº ßı
|
æº
|
Ł ı, º
|
øŁı
|
| ˝˛˜). ˇ æ {f
1
,f
2
,...,fs
} æŁæ
|
ª
|
º , æ Ł Œ
|
ßı
|
| Œ Ø Ø Ł ª º ºŁ
|
º , Ł d
Œ
|
ßØ
|
| º Ø ª º (d
6= 0). — æŁº Ł :
|
ß æº
|
øŁ
|
-
|
| 1) æ Œ æ ºŁ º Ø ª º
|
d
æ
|
æ æ Œ
|
æ
|
| ÆøŁı ºŁ º Ø æŁæ ß ª º
|
{f
1
,f
2
,...,fs
};
|
| 2) ª º d
º æ ÆøŁ ºŁ
|
º æŁæ ß ª
|
º
|
{f
1
,f
2
,...,fs
}, Œ ßØ ºŁ æ º Æ Ø ª Ø ÆøŁØ ºŁ º Ø æŁæ ß.
˜ Œ º æ . 1) ⇒ 2)
Œ Œ Œ æ Ł ºŁ º Ø ª º d
ı Ł æ æ ª º d
, æº Ł 1), d
º æ ÆøŁ ºŁ º {f
1
,f
2
,...,fs
}.
ˇ æ d
0
º Æ Ø ÆøŁØ ºŁ º {f
1
,f
2
,...,fs
}, ª
æº Ł 1) d
0
æ æ Ł Ł ºŁ º Ø ª º d
, æ d
ºŁ æ d
0
.
2) ⇒ 1)
´ß º Ł æº Ł 1) æ Ł ł ª . ) ˇ æ d
0
º Æ Ø ºŁ º ª º d
. ¨ d
0
|d
, æº Ł
2) (∀ 1 6 i
6 s
) d
|fi
⇒ (∀ 1 6 i
6 s
) d
0
|fi
, æ d
0
º æ ÆøŁ
ºŁ º æŁæ ß ª º {f
1
,f
2
,...,fs
}.
Æ) ˛Æ . ˇ æ d
0
º Æ Ø ÆøŁØ ºŁ º æŁæ ß ª º
{f
1
,f
2
,...,fs
}. ª æº Ł 2) ª º d
ºŁ æ d
0
, æ d
0
º æ ºŁ º ª º d
. 
˛ º Ł 6.3.5. ˝ ŁÆ º łŁ ÆøŁ ºŁ º (˝˛˜) æŁæ ß
ª º {f
1
,f
2
,...,fs
}, ß æ º Æ Ø º Ø ª º d
, º øŁØ º Æ Ł æŁº ßı æº ŁØ ß 6.3.1.
˛ º Ł 6.3.6. ˝˛˜ æŁæ ß ª º ß æ Œ Ø ÆøŁØ ºŁ º Ø æŁæ ß, Œ ßØ ºŁ æ º Æ Ø ª Ø ÆøŁØ ºŁ º Ø æŁæ ß ª º .
º æ Ł
6.3.1.1.
¯æºŁ ˝˛˜ æŁæ ß ª º æ ø æ ,
º æ æ ææ ŁŁ æ Ł.
˜ Œ º æ . ˇ æ d
1
, d
2
˝˛˜ æŁæ ß ª º
f
1
,f
2
,...,fs
, Æ ææ Ł d
1
Œ Œ ˝˛˜ æŁæ ß, d
2
Œ Œ ˛˜ æŁæ ß f
1
,f
2
,...,fs
. ª º Ł 6.3.6 d
2
|d
1
. ˇ º Ł d
1
Ł d
2
, æ d
1
Æ ææ Ł Œ Œ ˛˜, d
2
Œ Œ ˝˛˜
æŁæ ß f
1
,f
2
,...,fs
. ˇ º Ł 6.3.6 d
1
|d
2
, ª 3 æ Øæ ºŁ æ Ł d
1
∼ d
2
. 
´ ŁŒ æ æ ßØ æ: æ ø æ ºŁ ˝˛˜ æŁæ ß ª º {f
1
,f
2
,...,fs
}? ˛ æ º Ł º ßØ. Æ Ł æ æ º º æŁæ ß Ł 2-ı ª º . ß Œ æ ø æ Ł ˝˛˜ 2-ı ª º Ł Œ ºª Ł ª ı Ł .
ºª Ł ß æ ºª Ł ¯ ŒºŁ Ł æ æº º ª º Ł . ˇ æ f
Ł g
º ßı ª º , degf
> degg
. — ºŁ f g
æ æ Œ , º Ł
f
= q
1
g
+ r
1
,
ª r
1
= 0 ŁºŁ (r
1
= 06 Ł degr
1
<
degg
).
¯æºŁ r
1
= 0
, ææ º Ł Œ Ł æ . ¯æºŁ r
1
6= 0
, ºŁ g r
1
æ æ Œ , º Ł
g
= q
2
r
1
+ r
2
,
ª r
2
= 0 ŁºŁ (r
2
= 06 Ł degr
2
<
degr
1
).
¯æºŁ r
2
= 0
, ææ º Ł Œ Ł æ . ¯æºŁ r
2
6= 0
, ºŁ r
1
r
2
æ æ Œ , º Ł
r
1
= q
3
r
2
+ r
3
,
ª r
3
= 0 ŁºŁ (r
3
= 06 Ł degr
3
<
degr
2
).
¨ Œ º . ´ ŁŒ æ: ł ææ Œ ŁºŁ Æ æŒ ? ˙ Ł , æ Ł æ Œ Æ æ ª Æß ø æº -
º æ º ßı Łæ º, Ł degg >
degr
1
>
degr
2
>
degr
3
> ...
, Œ Æß Æ æŒ Ø. ´ Œ Œ º -
Ł æ
r
k
−2 = q
k
r
k
−1 + r
k
;
r
k
−1 = q
k
+1r
k
,
ª rk
æº ŁØ ßØ º æ Œ ºª Ł ¯ ŒºŁ .
¯˛—¯ 6.3.2. ˝ ŁÆ º łŁØ ÆøŁØ ºŁ º 2-ı º ßı ª -
º f
Ł g
æ ø æ Ł æº º æ Œ
ºª Ł ¯ ŒºŁ , Ł Œ ª º f
Ł g
.
˜ Œ º æ . ˙ Łł æ , º øŁ ºª Ł ¯ ŒºŁ
Œ ª º f
Ł g
f
= q
1
g
+ r
1
⇒ r
1
= f
− q
1
g
; (1) g
= q
2
r
1
+ r
2
⇒ r
2
= g
− q
2
r
1
; (2) r
1
= q
3
r
2
+ r
3
⇒ r
3
= r
1
− q
3
r
2
; (3)
...
r
k
−2 = q
k
r
k
−1 + r
k
⇒ r
k
= r
k
−2 − q
k
r
k
−1; (k
)
r
k
−1 = q
k
+1r
k
.
(k
+ 1) ¨ æº ª æ Ł , rk
|rk
−1
.
¨ æ (k
) Ł , rk
|rk
−2
.
¨ æ (k
− 1) Ł , rk
|rk
−3
.
... r
k
|r
2, r
k
|r
1
¨ æ (2) Ł , rk
|g
.
¨ æ (1) Ł , rk
|f
.
º º rk
º æ ÆøŁ ºŁ º æŁæ ß ª º
{f,g
}. ˇ æ d
º Æ Ø ÆøŁØ ºŁ º {f,g
}, ª
Ł æ (1) Ł , d
|r
1
, Ł æ (2) Ł , d
|r
2
,
...
Ł æ (k
) Ł , d
|rk
, æ rk
ÆøŁØ ºŁ º {f,g
}
, Œ ßØ ºŁ æ º Æ Ø ª Ø
ÆøŁØ ºŁ º {f,g
}. ª º Ł 6.3.6 rk
˝˛˜ {f,g
}. 
ø æ Ł ˝˛˜ º Æ Ø Œ Ø æŁæ ß ª º æ -
ºŁ æ æº ø Ø Ø, Œ Œ ª ı -
Ł .
¯˛—¯ 6.3.3 ( Œ º ). ˝˛˜ Œ Ø æŁæ -
ß ª º æ ø æ Ł Ł æ ºŁ æ ł Ł
HOD {f
1
,f
2
,...,fs
−1
,fs
} = HOD {HOD {f
1
,f
2
,...,fs
−1
},fs
}.
˜ Œ º æ . ˇ Ł Ł Ł æŒ Ø Ł Œ ŁŁ s
. ¯æ-
ºŁ s
= 2
, Ł ß Ł . ˇ º Ł ,
º (s
− 1)
ª º , æ ß º ª æ , æ ø æ ŁÆ º łŁØ ÆøŁØ ºŁ º d
æŁæ ß ª º
{f
1
,f
2
,...,fs
−1
}. ˛Æ Ł d
¯ = HOD {d,fs
}. ¨ , d
¯|d, d
¯|fs
,
Œ ª (∀ 1 6 i
6 s
− 1) d
|fi
, ª Ł Ł æ Ł ºŁ-
æ Ł (∀ 1 6 i
6 s
− 1) d
¯|fi
, d
¯|fs
, æº º d
¯ º æ ÆøŁ ºŁ º {f
1
,f
2
,...,fs
−1
,fs
}. ˇ æ d
0
º Æ Ø ÆøŁØ ºŁ º
{f
1
,f
2
,...,fs
−1
,fs
}, ª (∀ 1 6 i
6 s
− 1) d
0
|fi
Ł d
0
|fs
æº -
º d
0
º æ ÆøŁ ºŁ º {f
1
,f
2
,...,fs
−1
}. ª º Ł 6.3.6 d
0
|d
. ŒŁ Æ d
0
|d, d
0
|fs
æº º d
0
º æ ÆøŁ ºŁ º {d,f
s
}. ª Ł º Ł 6.3.6 æº d
0
|d
¯
.
¨ Œ d
¯ º æ ÆøŁ ºŁ º {f
1
,f
2
,...,fs
−1
,fs
} Ł d
¯ ºŁ æ º Æ Ø ÆøŁØ ºŁ º {f
1
,f
2
,...,fs
−1
,fs
}. ª º Ł 6.3.6
d
¯
= HOD {f
1
,f
2
,...,fs
−1
,fs
}. 
¯˛—¯ 6.3.4 (Œ Ł ŁØ ˝˛˜ æŁæ ß ª º ).
˜º ª Æß ª º d
º ºæ ˝˛˜ æŁæ ß ª º
{f
1
,f
2
,...,fs
} Æı Ł Ł æ , Æß ª º d
Æߺ
˛˜ Ø æŁæ ß Ł Æß ºŁ Ø ß ºæ Ł ª º -
ß, æ (∃ u
1
,u
2
,...,us
,
∈ k
[x
]) d
= u
1
f
1
+ u
2
f
2
+ ...
+ us
fs
.
˜ Œ º æ . 1) ˜ æ æ .
ˇ æ d
º æ ˛˜ {f
1
,f
2
,...,fs
} Ł ∃ u
1
,u
2
,...,us
∈ k
[x
] d
=
= u
1
f
1
+u
2
f
2
+...
+us
fs
. ˇ æ d
0
º Æ Ø ÆøŁØ ºŁ º {f
1
,f
2
,...,fs
}.
, (∀ 1
6 i
6 s
) d
0
|f
i
. ª 5 æ Øæ ºŁ-
æ Ł d
0
|(u
1
f
1
+ u
2
f
2
+ ...
+ us
fs
), æ d
0
|d
. ˇ º Ł 6.3.6 d
= HOD {f
1
,f
2
,...,fs
}.
2)˝ Æı Ł æ .
| ˇ æ d
º æ
|
˝˛˜ {f
1
,f
2
,...,fs
}.
|
ª
|
d
|
º
|
æ ˛˜
|
| {f
1
,f
2
,...,fs
}. ˛æ
|
æ Œ , d
ºŁ
|
Ø
|
ß
|
æ
|
| f
1
,f
2
,...,fs
. æ Ł
|
Œ
|
Ł
|
æŒ Ø Ł
|
Œ ŁŁ.
|
| ˇ æ
|
s
= 2. ˛Æ Ł
|
f
1
= f,f
2
= g
. ˙ Łł
|
æ
|
,
|
º -
|
| ø
|
ºª
|
Ł
|
¯ ŒºŁ
|
.
|
| f
= q
1
g
+ r
1
;
|
(1)
|
| g
= q
2
r
1
+ r
2
;
...
|
(2)
|
| r
k
−3 = q
k
−1r
k
−2 + r
k
−1;
|
(k
− 1)
|
| r
k
−2 = q
k
r
k
−1 + r
k
;
|
(k
)
|
| r
k
−1 = q
k
+1r
k
.
|
(k
+ 1)
|
| ¨
|
æ
|
,
|
˝˛˜ d
|
ª º {f,g
}
|
rk
. ¨
|
æ
|
(k
) Ł -
|
| ,
|
d
= r
k
−2 − q
k
r
k
−1 = r
k
−2 − q
k
(r
k
−3 − q
k
−1r
k
−2) =
= (1 + qk
qk
−1
)rk
−2
− qk
rk
−3
= ...
= ug
+ vf.
ˇ º Ł , Ł ß æ ºŁ º æŁæ ß, æ æ ø Ø Ł (s
− 1)
ª º . ˜ Œ æ ºŁ æ º æŁæ , æ æ øŁı Ł s
ª º . ˇ 6.3.3 ŁÆ º łŁØ ÆøŁØ ºŁ º d
æŁæ ß ª º {f
1
,f
2
,...,fs
} æ æ ˝˛˜
2-ı ª º {d
1
,fs
}, ª d
1
˝˛˜ {f
1
,...fs
−1
}. ˇ º Ł Ł Œ ŁŁ æ ø æ ª º ß v
1
,...,vs
−1
∈ k
[x
] ŒŁ ,
d
1
= v
1
f
1
+ v
2
f
2
+ ...
+ vs
−1
fs
−1
. ΠΠΠd
º æ ˝˛˜ {d
1
,fs
}, æ ø æ ª º ß w
1
,w
2
∈ k
[x
] ŒŁ , d
= w
1
d
1
+w
2
fs
. ¨
d
= w
1v
1f
1 + ··· + w
1v
s
−1f
s
−1 + w
2f
s
= u
1f
1 + u
2f
2 + ...
+ u
s
f
s
.  ˛ º Ł 6.3.7. ª º ß æ Ł ß , æºŁ ª æ łŁØ Œ Ł Ł 1. ˛ º Ł 6.3.7. ª º ß æ Ł ß , æºŁ ª æ łŁØ Œ Ł Ł 1.
æ , Œ Œº ææ ææ ŁŁ ßı ª º æ ø æ
Ł ßØ ª º . ´ æ æ Ł æ Ł ˝˛˜ æŁæ ß ª º -
, Œ ß º æ æ æ ææ ŁŁ æ Ł, æ ø æ Ł æ ßØ Ł ßØ ˝˛˜. Ł ßØ ˝˛˜
Æ Æ (f
1
,f
2
,...,fs
).
˛ º Ł 6.3.8. Łæ ª º {f
1
,f
2
,...,fs
} ß æ Ł æ Ø æ Œ æ Ł, æºŁ Ł ßØ ˝˛˜
(f
1
,f
2
,...,fs
) = 1. ´ æº ı ª º ª , Ł Ł æ ß .
¯˛—¯ 6.3.5 (æ Øæ Ł æ ßı ª º ).
ºŁ ß æº øŁ Ł .
1. Łæ ª º {f
1
,f
2
,...,fs
} Ł æ æ Œ æ Ł ª Ł º Œ ª , Œ ª Œ Łı ºŁ Ø Œ ÆŁ -
Ł Ł Ł , æ (∃ u
1
,...,us
∈ k
[x
]) u
1
f
1
+...
+us
fs
= 1;
2. ¯æºŁ ; ;
3. ¯æºŁ (f,h
) = 1 Ł (g,h
) = 1, (fg,h
) = 1;
4. ¯æºŁ h
|fg
Ł (h,g
) = 1 , h
|f
;
5. ¯æºŁ h
|f
Ł g
|f
Ł (h,g
) = 1, hg
|f
.
˜ Œ º æ . 1) ˇ º Ł 6.3.4 d
= 1. æ , d
-
º æ ˛˜ æŁæ ß {f
1
,f
2
...,fs
}, ª 6.3.4 d
= 1 Æ
˝˛˜ {f
1,f
2 ...,f
s
} ª Ł º Œ ª , Œ ª æ ø æ ª º ß
u
1
,u
2
,...,us
∈ k
[x
] ŒŁ , u
1
f
1
+ ...
+ us
fs
= 1.
2) ΠΠΠHOD{f
1
,f
2
...,fs
} = d
, 6.3.4 æ ø æ
ª º ß u
1
,u
2
,...,us
∈ k
[x
] ŒŁ , d
= u
1
f
1
+...
+us
fs
. — ºŁ
Æ æ Ł æ 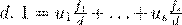 , Ł æ Øæ 1 æº , , Ł æ Øæ 1 æº ,
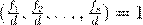 . .
3) ΠΠΠ(f,g
) = 1, 6.3.4 ∃ u,v
∈ k
[x
] 1 = uf
+
+ vh
. ΠΠΠ(g,h
) = 1, (∃ u
1
,v
1
∈ k
[x
]) 1 = u
1
g
+ v
1
h
. ˇ º
Ł Ł æ ł Ł . 1 = (uu
1
)fg
+ (vu
1
g
+ uv
1
f
+ vv
1
h
)h
. ˇ
æ Øæ 1 Ł ºŁ Ø Œ ÆŁ Ł ª º fg
Ł h
Ł Ł , æº º (fg,h
) = 1.
4) ΠΠΠ(h,g
) = 1, ∃ u,v
∈ k
[x
] uh
+ vg
= 1. Ł Æ æ Ł ª æ f
, º Ł uhf
+ vgf
= f
. ΠΠΠh
|fg
,
fg
= qh
, ª uhf
+ vqh
= f
⇒ (uf
+ vq
)h
= f
⇒ h
|f
.
5) ΠΠΠh
|f
, f
= qh
. ¨ g
|qh
Ł (g,h
) = 1, æ Øæ 4 º , g
|q
, æº º q
= q
1
g
. ŒŁ Æ f
= q
1
gh
⇒
⇒ gh
|f
. 
` ææ Ł æŁæ ª º {f
1
,f
2
,...,fs
},
Œ ßØ Ł Œ ßı º . ˜º ŒŁı æŁæ ª º Ł º -
Ł Ł Ł ł ª Æø ª Œ ª (˝˛˚) æı , º ªŁ Ø Ł Ł ˝˛˜.
˛ º Ł 6.3.9. ª º m
ß æ ÆøŁ Œ ß æŁæ ß
ª º {f
1,f
2,...,f
s
}, Œ ßØ Ł Œ ßı ºŁ º , æºŁ ºŁ æ æ ª º ß Ø æŁæ ß, æ (∀ 1
6 i
6 s
) f
i
|m
.
¯˛—¯ 6.3.6. ˇ æ {f
1
,f
2
,...,fs
} æŁæ º ßı ª -
º Ł m
6= 0 ( Œ ßØ º Ø ª º ). — æŁº ß æº øŁ Ł :
1) æ Œ æ Œ ßı ª º m
æ æ æ Œ æ
˛˚ æŁæ ß ª º {f
1
,f
2
,...,fs
};
2) ª º m
º æ ˛˚ {f
1
,f
2
,...,fs
}, Œ ºŁ º Æ ª ˛˚ Ø æŁæ ß.
| ˛ º
|
Ł 6.3.10. ˝ Ł łŁ ÆøŁ Œ
|
ß (˝˛˚) æŁæ
|
ß
|
| ª º
|
{f
1
,f
2
,...,fs
} ß
|
æ º Æ Ø
|
º Ø ª º
|
m
,
|
| º
|
øŁØ º Æ Ł
|
æŁº ßı æº
|
ŁØ ß 6.3.6.
|
| ˛ º
|
Ł 6.3.11. ˝˛˚ æŁæ
|
ß ª º
|
ß æ Œ
|
Æ-
|
| ø Œ
|
Ø æŁæ ß, Œ
|
ºŁ º Æ
|
ª Æø Œ
|
| Ø æŁæ
|
ß ª º .
|
| º æ Ł
|
6.3.6.1.
¯æºŁ ˝˛˚ æŁæ
|
ß ª º
|
æ ø æ ,
|
| º
|
æ æ ææ ŁŁ
|
æ Ł.
|
¯˛—¯ 6.3.7. ¯æºŁ æ ø æ ˝˛˚ 2-ı º Æßı º ßı -
ª º , æ ø æ ˝˛˚ Ł º Æ Ø Œ Ø æŁæ ß ª º -
, Ł Ł æ æº ø Ł Œ Ł º :
HOK{f
1
,f
2
,...,fs
−1
,fs
} = HOK{HOK{f
1
,f
2
,...,fs
−1
},fs
}.
6.3.7 æ Ł ı Ł ˝˛˚ æŁæ ß ª º Œ ı Ł ˝˛˚ 2-ı ª º .
¯˛—¯ 6.3.8. ¯æºŁ f
Ł g
º ßı ª º , Łı ˝˛˚
| ˜ Œ
|
º æ
|
. ˛Æ
|
Ł
|
ª
|
º
|
fg
. ´Ł
= m
(f,g
)
|
,
|
 æ ø æ Ł æ ø æ Ł 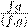 . .
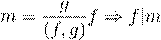
Ł
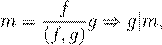
| æ m
º æ ˛˚ ª º {f,g
}. ˇ æ M
|
º Æ
|
˛˚ {f,g
}.
|
| , M
= uf, M
= vg
⇒ uf
= vg
. — ª æ (f,g
). ˇ º Ł
|
ºŁ
|
Æ æ Ł
|
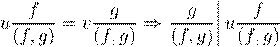 . .
ˇ æ Øæ 2 ß 6.3.5 Ł 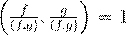 . ˇ 4 æ Øæ - . ˇ 4 æ Øæ -
ß 6.3.5 Ł 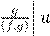 . ª u
= ( . ª u
= (
 f,g
g
)
q. M
= uf
= ( f,g
g
)
q. M
= uf
= (
 f,g
fg
)
q
= mq
. ´Ł , m
|M
. ˇ º Ł 6.3.11 m
º æ ˝˛˚ {f,g
}. f,g
fg
)
q
= mq
. ´Ł , m
|M
. ˇ º Ł 6.3.11 m
º æ ˝˛˚ {f,g
}. 
6.4 ˝ Ł Ł æ . ˚ Ł æŒ º Ł . ˚ æ
ˇ æ f
ª º º Ł º Ø æ Ł, α
∈ k
∗
= k
\{0
}. ¨ æ ,
α
|f
Ł αf
|f
.
˛ º Ł 6.4.1. Ł Ł º ß Ł ºŁ º Ł ª º f
º Ł-
º Ø æ Ł ß æ º ß Œ æ ß Ł ª º ß, ææ ŁŁ ß æ ª º f
.
º æ Ł .
˜ ºŁ º d
ª º f
º æ Ł Ł º ß ª Ł
º Œ ª , Œ ª 0 <
degd <
degf
.
º æ Ł .
ª º f
º Ł º Ø æ Ł Ł Ł Ł º ß
ºŁ ºŁ ª Ł º Œ ª , Œ ª ª æ Ł Ł Ł Ł 2-ı ª º , æ Ł Œ ßı ł æ Ł ª º
f
, æ (∃ u,v
∈ k
[x
]) f
= uv
, ª degu,
degv <
degf
.
˛ º Ł 6.4.2. ª º P
º Ł º Ø æ Ł ß æ Ł Ł ß º k
, æºŁ Ł Ł º º Œ Ł Ł º ß ºŁ ºŁ. ´ Ł æº , ª º P
ß æ
Ł Ł ß .
˛ º Ł 6.4.3. ª º P
º Ł º Ø æ Ł ß æ Ł Ł ß º k
, æºŁ ª º æ Ł Ł º Ł Ł Ł 2-ı ª º , æ Ł Œ ßı ł æ Ł
ª º P
.
˙ Ł
6.4.1.
ˇ Ł Ł Ł æ Ł æ ø æ ŁæŁ æ-
ª º k
. Œ, Ł , ª º f
= x
2
−2 = (x
+√2)( x
−√2) x
−√2)
Ł Ł º Q. ˝ Ł Ł º R.
˙ Ł
6.4.2.
ª º ß 1-Ø æ Ł º æ Ł Ł ß Ł º Æß º .
æº Ł ª , ª º ß 1-Ø æ Ł Ł º Œ Ł-
Ł º ß ºŁ ºŁ.
¯˛—¯ 6.4.1 (æ Øæ Ł Ł ßı ª º ). ºŁ ß æº øŁ Ł :
1. ¯æºŁ ª º P
º æ Ł Ł ß , Ł º Æ Ø ææ ŁŁßØ æ Ł ª º Œ º æ Ł Ł ß .
2. ¯æºŁ P
Ł Ł ßØ ª º , f
º Æ Ø ª º , ºŁÆ
(P,f
) = 1, ºŁÆ P
|f
.
3. ¯æºŁ P
Ł Ł ßØ ª º Ł P
|fg
, P
|f
ŁºŁ P
|g
.
4. ¯æºŁ P
Ł Q
Ł Ł ßı ª º , ºŁÆ (P,Q
) = 1, ºŁÆ P
Ł Q
ææ ŁŁ ß.
˜ Œ º æ . 1) ˇ æ P
Ł Ł ßØ ª º . — ææ Ł αP
, ª α
∈ k
∗
. ˝ Œ , αP
º æ Ł Ł ß . ˜ æ Ł Ł , æ αP
æ Ł Ł º ßØ ºŁ º , æ
(∃ d
∈ k
[x
]) d
|αP
, ª 0 <
degd <
degαP
= degP
. ¨ , d
|αP
Ł αP
|P
⇒ d
|P
Ł 0 <
degd <
degP
. Ł Ł Ł Ł æ Ł ª º P
.
2) ˛Æ Ł (P,f
) = d
. ¨ d
|P
. ΠΠΠP
Ł Ł , d
º Æß Ł Ł º ß ºŁ º , æ ºŁÆ d
= α
∈ k
∗
, ºŁÆ d
∼ P
. ´ æº Ł (P,f
) = 1. ´ æº , Ł P
|d
Ł d
|f
⇒ P
|f
.
3) ˇ æ P
|fg
. ¯æºŁ P
|f
, æ Œ . ¯æºŁ P
- f
, æ Øæ 2 (P,f
) = 1. ¨ Œ, P
|fg
Ł (P,f
) = 1, ª æ Øæ 4 ß 6.3.5
P
|g
.
4) ˇ æ P
Ł Q
Ł Ł ßı ª º . ¯æºŁ (P,Q
) = 1
,
æ Œ . ˇ æ (P,Q
) 6= 1, ª æ Øæ 2 P
|Q
. º Ł
P
Ł Q
, º Q
|P
⇒ P
∼ Q
. 
¯˛—¯ 6.4.2 ( º ŁŁ Ł Ł ß Ł ºŁ).
¸ Æ Ø ª º f
º Ł º Ø æ Ł º k
Æß
æ º Ł f
= αP
1
· P
2
· ...
· Ps
, ª α
∈ k
∗
, Pi
Ł -
ß Ł Ł ß k
ª º ß. æ º Ł Ł æ
æ æ Œ æº Ł æ Ł º Ø Ł Ł Æı Ł , Æß α
º º æ æ łŁ Œ Ł Ł ª º f
.
˜ Œ º æ . 1) ø æ Ł .
— ææ Ł æ M
æ ı Ł ßı ºŁ º Ø º Ł-
º Ø æ Ł ª º f
. ´ æ M
ßÆ ª º
P
1
Ł ł Ø æ Ł. ˇ Œ , ª º P
1
º æ Ł-
Ł ß . ˜ æ Ł Ł , æ ª º P
1
º æ Ł Ł-
ß . º º P
1
= du
, ª 0 <
degd <
degP
1
, Ł Ł
ßÆ ª º P
1
. ¨
f
= P
1
f
1
,
ª 0 6 degf
1
<
degf.
(1) ¯æºŁ degf
1
= 0
, ææ ß º Ł Ł Ł ßı Ł º Ø Œ Ł æ . ¯æºŁ degf
1
>
0
, æ ª º f
1
Ł ææ Ł , Ł æ ª º f
. ˇ º Ł , ª º f
1
æ Ł ßØ Ł Ł ßØ Ł º P
2
. ` Ł
f
1
= P
2
f
2
,
ª 0 6 degf
2
<
degf
1
.
(2)
¯æºŁ degf
2
= 0
, ææ ß º Ł Ł Ł ßı Ł º Ø -
Œ Ł . ¯æºŁ degf
2
>
0
, ææ º . ¨ Œ º . ´ Ł-
Œ æ: ł ææ Œ ŁºŁ Æ æŒ ? ˙ Ł , æ Ł ª º f
1
,f
2
,...
Æ æ ª Æß ø æº º æ
º ßı Łæ º degf >
degf
1
>
degf
2
> ...
, Œ Æß
Æ æŒ Ø. ´ Œ Œ º Ł
fs
−1
= Ps
fs
,
ª degfs
= 0.
(s
)
, f
s
= α
∈ k
∗. ˇ Ł º æ æ
(1),
(2),...,
(s
), º Ł f
= αP
1
·P
2
·...
·Ps
. Œ Œ ŒPi
º æ Łß Ł ª º Ł, æ Ł æ Œ Ł Ł ß Ł æ ł Ø æ Ł x
, º Ł , α
º æ æ łŁ Œ Ł Ł -
ª º f
.
2) ¯ Ł æ æ .
ˇ æ æ æ º Ł f
= αP
1
· P
2
· ...
· Ps
Ł æ
ª æ º Ł f
= βQ
1
· Q
2
· ...
· Qt
, ª β
∈ k
∗
, Qj
Ł ß Ł Ł ß k
ª º ß. ª , Œ ßł , β
º æ æ łŁ Œ Ł Ł ª º f
, æ β
= α
.
f
= αP
1
· P
2
· ...
· Ps
= βQ
1
· Q
2
· ...
· Qt
.
(∗)
— æ (∗) Œ ß , P
1
|(Q
1
· Q
2
· ...
· Qt
). ˇ æ Øæ 3 ß 6.4.1 (∃ 1 6 j
6 t
) P
1
|Qj
. ` æ Ł , P
1
|Q
1
. ª
æ Øæ 4 ß 6.4.1 P
1
∼ Q
1
. Œ Œ Œ Æ ª º Ł ß, P
1
= Q
1
. ª æ (∗) æ Œ ø P
1
. ˇ º Ł
P
2
· ...
· Ps
= Q
2
· ...
· Qt
.
(∗∗)
ª º P
2
ææ Œ , Œ Œ æ ª º P
1
. — æ
(∗∗) Œ ß , P
2
|(Q
2
·...
·Qt
) ⇒ (∃ 2 6 j
6 t
) P
2
|Qj
. ` æ Ł , P
2
|Q
2
. ª P
2
∼ Q
2
⇒ P
2
= Q
2
. ¨ Œ º . ¯æºŁ s
= t
,
Œ Œ º Ł Ps
= Qs
. ºŁ s
6= t
? ˇ º Ł , s < t
, ª æ Œ ø æ
(∗) P
1
· P
2
· ...
· Ps
º Ł , 1 = Qs
+1
· ...
· Qt
ª Æß
Œ Œ Œ æº æ Ł ª º º Ø æ Ł, æ ª -
º º Ł º Ø æ Ł. º ªŁ Æß Ł s > t
ŒŁ
Æ Qj
æ ß Pi
, º Œ Łæ ß ª Œ . 
¯˛—¯ 6.4.3 ( Œ Ł æŒ æ º ŁŁ). ¸ Æ Ø ª -
º f
º Ł º Ø æ Ł º k
Æß æ º
Ł 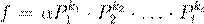 , ª α
∈ k
∗
, Pi
ºŁ ß Ł ß , Ł Ł ß k
ª º ß, ki
∈ N. æ º Ł , ª α
∈ k
∗
, Pi
ºŁ ß Ł ß , Ł Ł ß k
ª º ß, ki
∈ N. æ º Ł
Ł æ æ æ Œ æº Ł æ Ł º Ø Ł Ł α
Æı Ł º æ æ łŁ Œ Ł Ł ª º f
.
˜ Œ º æ . ˇ 6.4.2 Ł f
= αP
1
·P
2
·...
·Ps
. ˛Æœ Ł
æ º ŁŁ Ł Ł Ł Œ ßı Ł º Ø æ Ł,
º Ł
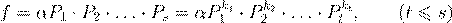 . .

˛ º Ł 6.4.4. ˇ æ º Ł ª º f
Ł 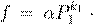  ß æ Œ Ł æŒŁ æ º Ł ª º ß æ Œ Ł æŒŁ æ º Ł ª º
f
. ª º ß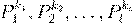 ß æ º ß Ł ºŁ º Ł ß æ º ß Ł ºŁ º Ł
ª º f
. ˝ º ß Łæº k
1
,k
2
,...,kt
ß æ Œ æ Ł Ł Ł ßı ª º P
1
,P
2
,...,Pt
ª º f
.
ˇ æ γ
∈ k
. ß ŁºŁ, ª º ß 1-Ø æ Ł Ł -
Ł ß º Æß º k
. ´ æ æ Ł x
− γ
º æ Ł ß
Ł Ł ß k
ª º , ª Ł Œ æ Ł
ª º x
− γ
ª º f
.
˛ º Ł 6.4.5. ˚ æ º γ
∈ k
ª º f
ßæ Œ æ Ł Ł ª ª º x
− γ
ª º f
.
˛ º Ł 6.4.6. º γ
∈ k
ß æ Œ ª º
f
(x
), æºŁ f
(γ
) = 0.
ˇ º Ł 6.4.1. ˜º ª , Æß º γ
∈ k
Æߺ Œ -
ª º f
(x
) Æı Ł Ł æ , Æß ª º f
ºŁºæ x
− γ
, æ , Æß º γ
Ł º º Ł º Œ æ
ª º f
.
˜ Œ º æ . ´ æ º , ` f
(x
) = Q
(x
)(x
− γ
) +
+ f
(γ
), ª (x
− γ
)|f
(x
) ⇔ f
(γ
) = 0, æ º Ł 6.4.6 γ
º æ Œ f
(x
). 
º æ Ł . º γ
∈ k
º æ Œ ª º f
(x
)
ª Ł º Œ ª , Œ ª º γ
Ł º Œ æ ª º
f
(x
).
˛ º Ł 6.4.7. ˚ γ
ª º f
(x
)
ß æ æ ß , æºŁ Ł Œ æ .
ˇ æ Œ Ł æŒ æ º Ł ª º f
Ł Ł
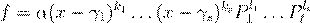 ,
ª degPi
> 2. ,
ª degPi
> 2.
´Ł ,
deg 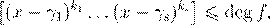 æ æ
k
1
+ k
2
+ ...
+ ks
6 degf.
æ , (∀ 1 6 i
6 s
) f
(γi
) = 0, æ γ
1
,γ
2
,...,γs
º æ Œ -
Ł ª º f
. ¯æºŁ Œ ßØ Œ γi
æ Ł ki
, Łæº k
1
+ k
2
+ ...
+ ks
Łæº Œ Ø ª º f
æ Łı Œ æ Ø.
ˇ º Ł 6.4.2. Łæº Œ Ø ª º f
(x
) æ Łı Œ -
æ Ø æı Ł æ ª º f
.
| 6.5
|
ˇ
|
Ł
|
Ł Œ
|
æ
|
| ˇ æ
|
k
|
Œ
|
ŁŒæŁ
|
Łæº
|
º .
|
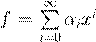 ˛ º Ł 6.5.1. ˇ Ł Ø ª ºß æ ˛ º Ł 6.5.1. ˇ Ł Ø ª ºß æ
ª º Ł
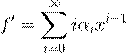 . .
| ¯˛—¯ 6.5.1 ( æ
|
ß Łº Ł
|
Ł Ł ).
|
| ¨ æ æº øŁ æ
1. α
0
= 0, ª α
∈ k
;
2. (αf
)0
= αf
0
, ª α
∈ k
;
3. (f
± g
)0
= f
0
± g
0
;
4. (fg
)0
= f
0
g
+ fg
0
;
5. (fn
)0
= nfn
−1
f
0
, n
∈ N.
|
Øæ :
|
| ˛ º Ł 6.5.2. ˇ º ª
|
f
(0) = f, f
(l
+1) = (f
(l
))0, ª
|
l
> 0, l
∈ Z.
|
| æ , æºŁ degf
= n
,
|
(∀ l > n
) f
(l
)
= 0.
|
| ¸ 6.5.1. ¯æºŁ f
ª
Ł degf
0
= n
− 1.
|
º º Ł º Ø æ
|
Ł n
, f
0
6= 0
|
˜ Œ º æ . ¨ f
= αn
xn
+...
+α
1
x
+α
0
, ª αn
6= 0, n
> 1. ˇ
º Ł 6.5.1 f
0
= nαn
xn
−1
+...
+α
1
. łŁØ Œ Ł Ł -
ª º f
0
nαn
, ª n
∈ N, αn
6= 0. ª nαn
6= 0, æº º
f
0
6= 0 Ł degf
0
= n
− 1. 
¯˛—¯ 6.5.2. ˇ æ f
ª º º Ł º Ø æ Ł Ł
Ł Ł ßØ Ł º P
Ł º Ł º Œ æ k
ª º f
. ª Ł Ł ßØ Ł º P
Ł Œ æ k
− 1 Ł Ø f
0
.
6.5. ˇ Ł Ł Œ æ
˜ Œ º æ . ¨ f
= P l
g
, ª P
- g
. æ Ł f
0
= lP l
−1
P
0
g
+
+ P l
g
0
= P l
−1
(lP
0
g
+ Pg
0
). ´Ł , P l
−1
|f
0
, æ Œ æ P f
0
ł , l
−1
. ˇ Œ , P l
- f
0
. ˜ æ Ł Ł , æ
P l
|f
0
. ª P
|(lP
0
g
+ Pg
0
). ´Ł , P
|Pg
0
, æº º P
|(lP
0
g
). æ , (P,l
) = 1. ˇ º P
0
6= 0 Ł degP
0
<
degP
⇒ (P,P
0
) = 1. ˇ æ Øæ 3 ß 6.4.1 Ł , P
|g
, Ł Ł , . º º P l
- f
0
Ł Œ æ P
æ æ f
0
l
− 1
.  º æ Ł
6.5.2.1.
º γ
Ł Œ æ k
ª º f
ª Ł º æ Ł
6.5.2.1.
º γ
Ł Œ æ k
ª º f
ª Ł
º Œ ª , Œ ª f
(γ
) = f
0
(γ
) = ...
= f
(k
−1)
(γ
) = 0, f
(k
)
(γ
) 6= 0.
˜ Œ º æ . 1) ˝ Æı Ł æ .
ˇ æ γ
Ł Œ æ k
ª º f
. ˇ º Ł -
, (x
− γ
)
Ł Œ æ k
ª º f
. ˇ 6.5.2
x
− γ
Ł Œ æ k
− 1 f
0
, x
− γ
Ł Œ æ k
− 2 f
00
, ..., x
−γ
Ł Œ æ 1 f
(k
−1), x
−γ
Ł Œ æ 0 f
(k
). ˇ Ł
º Ł 6.4.1 f
(γ
) = f
0
(γ
) = ...
= f
(k
−1)
(γ
) = 0, f
(k
)
(γ
) 6= 0.
2) ˜ æ æ .
ˇ æ f
(γ
) = f
0
(γ
) = ...
= f
(k
−1)
(γ
) = 0, f
(k
)
(γ
) 6= 0. ˇ æ Œ -
æ γ
ª º f
l
.˝ Œ , l
= k
. ˜ æ Ł
Ł . ˇ æ , Ł , l < k
. ª Ø æ Ł Œ º -
æ Æ Ł f
(γ
) = f
0
(γ
) = ...
= f
(l
−1)
(γ
) = 0, f
(l
)
(γ
) 6= 0. ª
Æß , æº Ł f
(l
)
(γ
) = 0 ΠΠΠl
6 k
−1. -
º ªŁ Ł Ł Œ Ł Ł Ł º Ł , l > k
. 
º æ Ł 6.5.2.2. ˚ æ º γ
ª º f
Ł ł Œ Ł Ø ª º f
, Ł ø ª γ
æ Ł Œ .
¯˛—¯ 6.5.3 ( Æ º ŁŁ Œ ßı Ł º Ø). ˇ æ
f
ª º º Ł º Ø æ Ł º k
. ª ª º 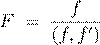 Ł æ ß Ł Ł ß Ł ºŁ, Ł Ł æ ß Ł Ł ß Ł ºŁ, Ł
ª º f
, º Œ Ø Œ æ Ł.
˜ Œ º æ . ˇ æ 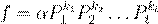 Œ Ł æŒ º Ł Œ Ł æŒ º Ł
ª º f
. ª 6.5.2
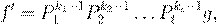 ª (∀ 1 6 i
6 t
) Pi
- g. ª (∀ 1 6 i
6 t
) Pi
- g.
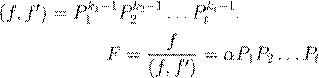 æ Ł æ Ł
.

| 6.6 ºª Æ Ł
|
æŒŁ Œ ß
|
º
|
| ˇ æ k
æ
|
º .
|
| ¯˛—¯ 6.6.1 (
|
æŁº ßı æº
|
Ł ı, º øŁı º-
|
| ª Æ Ł æŒŁ Œ
|
º ). ˛ æŁ
|
º ŁŒæŁ
|
ª æ-
|
| ª º k
æ
|
ºŁ ß æº øŁ
|
æŁº ß
|
Ł .
|
| 1) º Æ Ø ª º
|
f
º Ł º Ø æ
|
Ł æ Œ Ł Ł
|
Ł Ł
|
| º k
, Ł
|
º k
, Œ Ø Ø
|
, Ł Œ ;
|
| 2) Ł Ł ß Ł æ Ł;
|
º k
º æ
|
ª º ß º Œ
|
Ø
|
| 3) ª º º
ºŁ;
|
k
æ æ º
|
k
ºŁ Ø ß
|
Ł-
|
| 4) º Æ Ø ª º
|
f
º Ł º Ø æ
|
Ł æ Œ Ł Ł
|
Ł Ł
|
| º k
Ł
|
º k
æ º Œ Œ Ø æ Łı Œ
|
æ Ø,
|
Œ Œ æ ª º f
.
˜ Œ º æ . 1) ⇒ 2)
ˇ æ f
º Æ Ø ª º , degf
> 2. ª æº Ł 1)
ª º Ł º k
Œ Ø Ł Œ γ
. ª -
º Ł 6.4.1 f
= (x
−γ
)g
. º º f
º æ Ł Ł ß k
.
6.6. ºª Æ Ł æŒŁ Œ ß º
2) ⇒ 3)
| ˇ æ f
ª º º Ł º Ø æ Ł. ª 6.4.2
ª æ Ł Ł f
= αP
1
· P
2
· ...
· Ps
, ª α
∈ k
∗
, Pi
Ł ß Ł Ł ß k
ª º ß. ¨ æº Ł 2) æº ,
Pi
= x
− γi
⇒ f
= α
(x
− γ
1
)(x
− γ
2
)...
(x
− γn
). ŒŁ Æ
|
| ª º æ æ ºŁ Ø ß Ł ºŁ.
3) ⇒ 4)
|
| ¨ f
= α
(x
− γ
1
)(x
− γ
2
)...
(x
− γs
). ˛Æœ
Ł Œ ßı Ł º Ø æ Ł.
|
Ł Ł Ł Ł
|
| f
= (x
− γ
1
)k
1
(x
− γ
2
)k
2
...
(x
− γt
)k
t
,
|
ki
∈ N.
|
| ´Ł , γ
1
,...,γt
Œ Ł ª º f
æ Œ
|
æ Ł k
1
,...,kt
Ł
|
| degf
= k
1
+...
+kt
. ŒŁ Æ Łæº Œ Ø
Łı Œ æ Ø æ Ł ª º f
.
4) ⇒ 1)
|
ª º f
æ
|
| ˇ æ ª º f
Ł deg >
0
. ª æº
|
Ł 4) k
1
+k
2
+...
+
|
| + kt
= degf
> 1 ⇒ (∃ 1 6 i
6 t
) ki
> 1. ˙ Ł ,
|
ª º f
Ł
|
Œ Ø Ø Œ γi
. 
˛ º Ł 6.6.1. ˇ º k
ß æ ºª Æ Ł æŒŁ Œ ß , æºŁ º º Æ Ł æŁº ßı æº ŁØ ß 6.6.1.
˙ Ł
6.6.1.
ˇ º Q Ł R º æ ºª Æ Ł æŒŁ Œ ß Ł, Œ Œ Œ ß º æ 1) æº Ł ß 6.6.1. ˇ Ł æº -
Ł ª º f
= x
2
+ 1
. ˛ Ł Ł ª Œ Ł º Q,
Ł º R.
˛ º Ł 6.6.2. ºª Æ Ł æŒŁ ߌ Ł º k
ß æ Ł ł ºª Æ Ł æŒŁ Œ æłŁ Ł º k
.
˛ º Ł 6.6.3. ˇ º k
 ß æ ºª Æ Ł æŒŁ ߌ Ł º k
, æºŁ ß º ß æº øŁ 3 æº Ł : ß æ ºª Æ Ł æŒŁ ߌ Ł º k
, æºŁ ß º ß æº øŁ 3 æº Ł :
| 2. k
º æ ºª Æ Ł æŒŁ Œ ß º ;
|
| 3. æºŁ k
⊂ k
0
⊂ k
Ł k
0
ºª Æ Ł æŒŁ Œ º ,
|
k
0
= k
.
|
| ¯˛—¯ 6.6.2 ( æ ºª Æ ß). ˇ º Œ
Łæ º C º æ ºª Æ Ł æŒŁ Œ ß º .
|
º Œæ ßı
|
| º æ Ł
6.6.2.1.
ºª Æ Ł æŒŁ ߌ Ł º Øæ Łæ º R º æ º Œ º Œæ ßı Łæ º, æ R = C.
|
Ł º ßı
|
| ˜ Œ º æ . ˜ Øæ Ł º , æ R ºª Æ Ł æŒ
|
ߌ Ł
|
     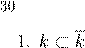 ; ;
     º R. ª R ⊂ R. ˜ º , ª º x
2
+1
Ł Œ R, æ i
∈ R. ß º æ ª Ł º Œ ª , Œ ª (∀ x,y
∈ R) x
+ +yi
∈ R, æ C ⊂ R. ¨ R ⊂ C ⊂ R. ˇ 6.6.2 C º æ ºª Æ Ł æŒŁ Œ ß , ª º Ł 6.6.3 Ł C = R. º R. ª R ⊂ R. ˜ º , ª º x
2
+1
Ł Œ R, æ i
∈ R. ß º æ ª Ł º Œ ª , Œ ª (∀ x,y
∈ R) x
+ +yi
∈ R, æ C ⊂ R. ¨ R ⊂ C ⊂ R. ˇ 6.6.2 C º æ ºª Æ Ł æŒŁ Œ ß , ª º Ł 6.6.3 Ł C = R.
ˇ æ γ
1
,γ
2
,...,γn
º ß º k
.
˛ º Ł 6.6.4. º ß Ł æŁ Ł æŒŁ Ł ª º Ł º γ
1,...,γ
n
ß æ æ ß Ł :
σ
1
= γ
1
+ γ
2
+ ...
+ γn
;
σ
2
= γ
1
γ
2
+ γ
1
γ
3
+ ...
+ γ
1
γn
+ γ
2
γ
3
+ ...
+ γ
2
γn
+ ...
+ γn
−1
γn
;
...
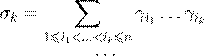 ; ;
σn
= γ
1
...γn
.
ˇ º Ł 6.6.1. ¯æºŁ γ
1
,γ
2
,...,γn
∈ k
,
f
(x
) = (x
+γ
1
)(x
+γ
2
)...
(x
+γn
) = xn
+σ
1
xn
−1
+...
+σk
xn
−k
+...
+σn
,
ª σ
1
,σ
2
,...,σn
º ß æŁ Ł æŒŁ ª º ß
γ
1
,γ
2
,...,γn
.
6.6. ºª Æ Ł æŒŁ Œ ß º
˜ Œ º æ . Æß æ Ł Œ , æ -
Ł æŒ ÆŒŁ æ øŁ æº Ł Ł æ Ł Æ ß æº ª ß . 
º æ Ł . ¯æºŁ γ
1
,γ
2
,...,γn
∈ k
, f
(x
) = (x
− γ
1
)(x
− γ
2
)...
(x
−
− γ
n
) = x
n
− σ
1x
n
−1 + σ
2x
n
−2 − ...
+ (−1)k
σ
k
x
n
−k
+ ...
+ (−1)n
σ
n
,
ª σ
1
,σ
2
,...,σn
º ß æŁ Ł æŒŁ ª º ß
γ
1
,γ
2
,...,γn
.
| ˜ Œ
|
º æ
|
. ´ æ
|
º , æ º
|
ŁŁ 6.6.1
|
æ
|
| γi
|
æ
|
Ł
|
−γi
. ª
|
σk
Ł æ (−1)k
σk
Ł
|
æ ß æº
|
æ Ł
|
Æ æ º . 
| ¯˛—¯ 6.6.3 (
|
´Ł
|
). ˇ æ
|
f
(x
) = xn
+ α
1
xn
−1
+
|
| + α
2
xn
−2
+ ...
+ αn
Ł
|
ª
|
º Ł
|
ºª Æ Ł æŒ ß-
|

Œ ŁŁ k
Œ Ł γ
1
,γ
2
,...,γn
. ª σk
= (−1)k
αk
, ª σ
1
,σ
2
,...,σn
º ß æŁ Ł æŒŁ ª º ß Œ Ø γ
1
,γ
1
,...,γn
.
˜ Œ º æ . ˝ º k
 ª º ª º
f
(x
) = (x
− γ
1
)(x
− γ
2
)...
(x
− γn
),
ª γ
1
,γ
2
,...,γn
Œ Ł f
(x
) k
. ˇ æº æ Ł Ł º Ł 6.6.1
Ł :
f
(x
) = xn
− σ
1
xn
−1
+ σ
2
xn
−2
− ...
+ (−1)k
σk
xn
−k
+ ...
+ (−1)n
σn
.
ª Ø æ ß, æº Ł f
(x
) = xn
+α
1
xn
−1
+...
+αn
. ŒŁ Æ -
Ł ß Ł ª Ł ª ª º Æß øŁ æ x
. ª , Œ Ł Ł ß Ł Ł Œ ßı æ ı x
º ß æ . ¨ −σ
1
= α
1
, σ
2
= α
2
,...,
(−1)k
σk
= αk
,...,
(−1)n
σn
=
= αn
. ¨ (∀ 1 6 k
6 n
) (−1)k
σk
= αk
. Ł (−1)k
, º Ł
σk
= (−1)k
αk
.
32
 æ ßØ æº Ø ß 6.6.3: æ ßØ æº Ø ß 6.6.3:
n=2, f
(x
) = x
2
+ px
+ q
. ˇ æ x
1
, x
2
Œ Ł f
(x
), ª
( σ
1
= x
1
+ x
2
= −p
; σ
2
= x
1
· x
2
= q.
n=3, f
(x
) = x
3
+ px
2
+ qx
+ r
. ˇ æ x
1
, x
2
x
3
Œ Ł f
(x
), ª
σ
1 = x
1 + x
2 + x
3 = −p
; σ
2
= x
1
x
2
+ x
1
x
3
+ x
2
x
3
= q
; .
σ
3 = x
1x
2x
3 = −r
6.7 ª º ß Łæº ß Ł º Ł
— ææ Ł æº Ø, Œ ª k
=
C. ˇ æ Ø ºª Æ ß, º
C º æ ºª Æ Ł æŒŁ Œ ß , ª º ß º
C ƺ º Æß Ł æŁº ßı æº ŁØ ß 6.6.1. ´ æ æ Ł, Ł Ł ß Ł º C º æ ª º ß º Œ Ø æ Ł. ˜ º , º Æ Ø ª º º Ł º Ø æ Ł º C Ł , Œ Ø , Ł Œ . ˝ Œ , Œ Ł æŒ º Ł º Æ ª ª º f
º Ł º Ø æ Ł º C Ł Ł :
f
(x
) = α
(x
− γ
1
)k
1
(x
− γ
2
)k
2
...
(x
− γt
)k
t
,
ª γ
1
,γ
2
,...,γt
∈ C.
— ææ Ł æº Ø, Œ ª k
= R. ˇ æ γ
= α
+βi
, ª α,β
∈ R, β
6=
6= 0
. ´ æº ª , γ
æ ø æ Œ º Œæ Łæº .
ˇ º Ł 6.7.1. ¯æºŁ γ
æ ø æ Œ º Œæ Łæº ,
 ª º (x
−γ
)(x
−γ
) º æ Œ ß ı º æ Øæ Łº ß Ł Œ Ł Ł Ł Ł Ł º ß ŁæŒ Ł Ł . ª º (x
−γ
)(x
−γ
) º æ Œ ß ı º æ Øæ Łº ß Ł Œ Ł Ł Ł Ł Ł º ß ŁæŒ Ł Ł .
˜ Œ º æ . ˜ Øæ Ł º , (x
− γ
)(x
− γ
¯) = x
2
− (γ
+ ¯γ
)x
+ γγ
¯ =
= x
2
−2αx
+α
2
+β
2
∈ R[x
], ª D
= (−2α
)2
−4(α
2
+β
2
) = −4β
2
<
0,
Œ Œ Œ γ
æ ø æ Œ º Œæ Łæº .
6.7. ª º ß Łæº ß Ł º Ł
¯˛—¯ 6.7.1. ¯æºŁ æ ø æ Œ º Œæ Łæº γ
º æ
Œ ª º f
æ Øæ Ł º ß Ł Œ Ł Ł Ł, Œ -
º Œæ æ Łæº γ
¯ Œ º æ Œ ª ª º Ł Ł Ø Œ æ Ł, Ł Œ γ
.
˜ Œ º æ . ˇ æ f
(x
) = αn
xn
+ ...
+ α
1
x
+ α
0
, ª αi
∈ R Ł γ
æ ø æ Œ º Œæ ßØ Œ f
(x
), æ f
(γ
) = 0.
αn
γn
+ ...
+ α
1
γ
+ α
0
= 0.
ˇ Ø Œ Œ º Œæ æ ß Łæº , º Ł

αn
γn
+ ...
+ α
1
γ
+ α
0
= 0.
´ æ º æ æ Øæ Ł Œ º Œæ æ ßı Łæ º, Ł
α
¯n
· γ
¯n
+ ...
+ ¯α
1
· γ
¯ + ¯α
0
= ¯0.
Œ Œ Œ αi
Ł 0 ∈ R, α
¯i
= αi
,
¯0 = 0. ˇ º
αn
(¯γ
)n
+ ...
+ α
1
γ
¯ + α
0
= 0.
æ Œ ß , f
(¯γ
) = 0 æ γ
¯ º æ Œ
ª º f
(x
)
. ˇ Œ , Œ æ Œ γ
¯
æ æ Œ æ Œ γ
. ˇ æ Œ æ γ
k
, Œ æ γ
¯ l
. ˝ Æı Ł Œ , k
= l
. ˜ æ Ł Ł , æ k
6= l
. ˇ æ ,
Ł , k > l
, ª f
= (x
− γ
)k
(x
− γ
¯)l
g
(x
), ª g
(γ
) 6= 0,g
(¯γ
) = 06.
ª f
(x
) = [(x
− γ
)(x
− γ
¯)]l
(x
− γ
)k
−l
g
(x
) = [(x
− γ
)(x
− γ
¯)]l
g
1
(x
),
æ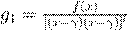 . ˇ º Ł (x
− γ
)(x
− γ
¯) ∈ R[x
], . ˇ º Ł (x
− γ
)(x
− γ
¯) ∈ R[x
],
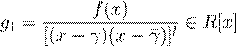 . .
´Ł , g
1
(x
) = (x
− γ
)k
−l
g
(x
) Ł γ
æ Ł Œ º Ł º Ø
Œ æ Ł, k
− l >
0, Ł æ Ł Œ γ
¯. Ł Ł
Ł Œ ß Ø Ø. º ªŁ Ł Ł Œ Ł Ł º Ł , l > k
.
34
º æ Ł
6.7.1.1.
ø æ Œ º Œæ ß Œ Ł ª º æ Øæ Ł º ß Ł Œ Ł Ł Ł Œ º Œæ æ ß.
¯˛—¯ 6.7.2 ( Ł Ł ßı ª º ı R). ˝ -
º Øæ Ł º ßı Łæ º R Ł Ł ß Ł º æ ª º ß
Ø æ Ł Ł Ł º Œ Œ ß ı º ß, ŁæŒ Ł ŁŒ ßı Ł º ßØ.
˜ Œ º æ . ˇ æ f
(x
) ∈ R[x
] Ł degf
(x
) > 3. ª º
 Ł ºª Æ Ł æŒ ßŒ ŁŁ R = C Ł Œ Ø Ł Ł ºª Æ Ł æŒ ßŒ ŁŁ R = C Ł Œ Ø Ł
Œ α
. ¯æºŁ α
∈ R , f
(x
) = (x
− α
)g
(x
), ª g
(x
) ∈ R[x
] æ
ª º f
Ł Ł R. ¯æºŁ α
æ ø æ Œ º Œæ Łæº , α
¯
Œ Æ Œ ª º f
. ˇ º Ł
f
(x
) = (x
− α
)(x
− α
¯)g
(x
) = (x
2
− 2Reα
· x
+ |α
|2
)g
(x
).
´ æº
 . .
´Ł , f
(x
)
æ Ł Ł R. ŒŁ Æ , º Æ Ø ª º f
, æ Œ ª degf
> 3, º æ Ł Ł ß R.
ˇ æ f
= ax
2
+bx
+c,a
6= 0. ¨ æ , Œ ßØ ı º æ æ ºŁ Ø ß Ł ºŁ f
= a
(x
−x
1
)(x
−x
2
) R ª Ł
º Œ ª , Œ ª ª ŁæŒ Ł Ł D
> 0. ´ æº , ª º
f
Ł Ł R. º º , Æ Ł Ł R ª Ł º Œ ª , Œ ª D
= b
2
− 4ac <
0. ª º ß Ø æ Ł º æ Ł Ł ß Ł º Æß º . 
º æ Ł
6.7.2.1.
¸ Æ Ø ª º º Ł º Ø æ Ł º Øæ Ł º ßı Łæ º Ł Œ Ł æŒ æ º Ł Ł :
f
= α
(x
− γ
1
)k
1
...
(x
− γt
)k
t
(x
2
+ β
1
x
+ δ
1
)l
1
...
(x
2
+ βr
x
+ δr
)l
r
,

 ª α,βi
,δi
,γj
∈ R, βi
2
− 4δi
<
0, kj
,li
∈ N Ł i
= 1,r, j
= 1,t
. ª α,βi
,δi
,γj
∈ R, βi
2
− 4δi
<
0, kj
,li
∈ N Ł i
= 1,r, j
= 1,t
.
6.7. ª º ß Łæº ß Ł º Ł
º æ Ł
6.7.2.2.
¸ Æ Ø ª º æ Øæ Ł º ß Ł Œ Ł Ł -
Ł Ø æ Ł Ł , Œ Ø , Ł Øæ Ł º ßØ Œ .
˜ Œ º æ . ´ æ º , æº æ Ł 6.7.2.1 degf
= k
1
+ ...
+ +kt
+2l
1
+...
+2lr
. ˇ æº Ł æ f
Łæº , æº º k
1
+ ...
+ kt
Łæº , Ł (∃ 1 6 i
6 t
) ki
> 1, æ γi
º æ Øæ Ł º ß Œ ª º f
. 
ˆº 7
˛æ ß ºª Æ Ł æŒŁ æ Œ ß
36
ˆº 8
¸Ł Ø ß æ æ
8.1 ˇ Ł ºŁ Ø ª æ æ
˛ º Ł 8.1.1. ˇ æ k
Ł V
Ł º ßı æ . ˆ -
, æ V
º ł ºª Æ Ł æŒ Ł æ æ º Ł ºŁŒ k
, æºŁ Æ Ł Œ ª Ł Ł k
× V
→ V
. ˇ Ł Æ ŁŁ, Æ -
ßØ ß (α,a
), ª α
∈ k, a
∈ V
ß æ Ł Ł α a
Ł Æ æ αa
.
˙ Ł
8.1.1.
ºª Æ Ł æŒŁ ŁŁ, Ł ß æ V
, ß æ Ł Ł ºª Æ Ł æŒŁ Ł Ł Ł. ´ Œ æ æ k
ø æ ª Æ ßæ º , Œ Æ ßæ ß . º ß º k
Æ Æ α,β,γ,α
1
,α
2
,...
˛ º Ł 8.1.2. ¸Ł Ø ß ( Œ ß ) æ æ º
k
ß æ æ V
, ææ æ æ º Ø
Ø ºª Æ Ł æŒ Ø Ł Ø æº Ł Ł ł Ø ºª Æ Ł æŒ Ø Ł Ø Ł æŒ º ß º k
, º ß Ł æº øŁ æ Ł ŒæŁ .
1. a
+ b
= b
+ a
;
2. a
+ (b
+ c
) = (a
+ b
) + c
;
37
3. (∀ a,b
∈ V
) (∃ x
∈ V
) b
+ x
= a
;
4. α
(a
+ b
) = αa
+ αb
;
5. (α
+ β
)a
= αa
+ βa
;
6. (αβ
)a
= α
(βa
) = β
(αa
);
7. 1 · a
= a
,
ª a,b,c,x
∈ V
; α,β,
1 ∈ k
.
˙ Ł
8.1.2.
æ V
æ ß Æ Łæ ß æ
ºŁ Ø ª æ æ . ¯ª º ß Æ Æ a,b,c,a
1
,a
2
,...
Ł ß Œ Ł.
Øæ ºŁ Ø ßı æ æ
1. (∀ a
∈ V
) (∃ 0 ∈ V
) a
+ 0 = a
;
2. (∀ a
∈ V
) (∃ (−a
) ∈ V
) a
+ (−a
) = 0;
3. (∀ a,b
∈ V
) (∃ (a
− b
) ∈ V
) a
− b
= a
+ (−b
);
4. αa
= 0 ⇔ α
= 0 ŁºŁ a
= 0;
5. α
(−a
) = (−α
)a
= −αa
;
6. α
(a
− b
) = αa
− αb
;
7. (α
− β
)a
= αa
− βa
.
˜ Œ º æ . ŒæŁ ß 1 3 ºŁ Ø ª æ æ Œ ß , (V,
+)
Æ Ł Ł ª , æ ºŁ ß æ Øæ 1) 3).
4) ˝ Æı Ł æ .
¨ αa
= (α
+ 0)a
= αa
+ 0a
⇒ 0a
= αa
− αa
= 0. ˇ º ,
0a
= 0.
8.2. ` Łæ ºŁ Ø ª æ æ
¨ αa
= α
(a
+ 0) = αa
+ α
0 ⇒ α
0 = αa
− αa
= 0. ˇ º ,
α
0 = 0.
˜ æ æ .
ˇ æ αa
= 0
. ¯æºŁ α
= 0
, æ Œ . ¯æºŁ α
6= 0
Æ æ ø -
æ α
−1
∈ k
. ª a
= 1 · a
= (α
−1
α
)a
= α
−1
(αa
) = α
−1
· 0 = 0.
5) — æ Ł αa
+ α
(−a
) = α
(a
+ (−a
)) = α
· 0 = 0 ⇒ α
(−a
) = −αa
.
˜ º , αa
+ (−α
)a
= (α
+ (−α
))a
= 0 · a
= 0 ⇒ (−α
)a
= −αa
.
6) ¨ , α
(a
− b
) = α
(a
+ (−b
)) = αa
+ α
(−b
) = αa
− αb
.
7) ˇ æ Ł (α
− β
)a
= (α
+ (−β
))a
= αa
+ (−β
)a
= αa
− βa
. 
| ˇ Ł ß ºŁ Ø ßı æ æ
:
|
| 1. V
= {0} º ºŁ Ø
|
æ
|
æ ( Ł Ł º
|
).
|
| 2. V
= kn
= {(α
1
,...,αn
)|αi
∈ k
} æ º k
.
|
Œ
|
Ł ºŁ Ø
|
æ -
|
| 3. V
= M
(m
×n,k
) Ł ß
|
æ Ł m
×n
æ º
|
Ł Ł k
.
|
| 4. V
= L
æ ł ŁØ
ŁØ.
|
Ø æŁæ ß ºŁ
|
Ø ßı -
|
| 5. V
= k
[x
] æ ª º Ł Ł Ł Ł k
.
6. V
= {f
(x
) ∈ k
[x
]|deg f
6 n
}.
|
ª Ł æ
|
ª æ Œ -
|
| 8.2 ˚ ß Ł Æ æŒ
|
ß
|
ºŁ Ø ß
|
| æ æ . ` Łæ ºŁ
|
Ø ª æ
|
æ
|
| ¸ ªŒ Ł , æ ß Ł
|
Ł Œ ß, º
|
ß Œ -
|
| Ł ºŁ Ø æ æ
|
æ æ Ææ Œ
|
ß ºŁ Ø ß
|
æ æ . æ , Ł Ł Ł Œ ß Łæ º ºŁ
º Œ æ Øæ ŁØ Œ Ł, Łæ º ºŁ Ł
æ Łı Œ . Œ Œ Ł Ł º Ł 8.1.2, ŁŁ Ææ Œ ºŁ Ø æ æ ƺ Ł æ ß Ł æ Øæ Ł, Ł
ŁŁ Œ Ł ºŁ Ø æ æ . ˇ , Ææ Œ ßı ºŁ Ø ßı æ æ ı ª Ł ºŁ Ø Ø Œ ÆŁ ŁŁ Œ , ºŁ Ø ŁæŁ ßı Ł ºŁ Ø ŁæŁ ßı æŁæ ı Œ , Œ Ł ŁŁ Ł æ Øæ ı ºŁ Ø Ø ŁæŁ æ Ł, Æ æ Ø
ºŁ Ø Ø ŁæŁ æ Ł, ºŁ Ø ß ŁŁ Ø æŁæ ß Œ -
ª , Æ Œ Ł º ßı æŁæ ı Œ , Æ Łæ Ł ª æŁæ ß Œ . ˝ æ Ł ºŁ Ł .
ˇ Ł
: V
= k
[x
]
. — ææ Ł æº ø æŁæ Œ :
1,x,x
2
,...,xn
∈ V
. æŁæ Œ º æ ºŁ Ø ŁæŁØ. ˜ Øæ Ł º ,
α
0
· 1 + α
1
x
+ α
2
x
2
+ ...
+ αn
xn
= 0 ⇔ α
0
= α
1
= α
2
= ...
= αn
= 0,
Ł , 1,x,x
2,...,x
n
º æ ºŁ Ø ŁæŁ Ø æŁæ -
Ø Œ . ł æ , n
Æ º Æß Ł Œ Œ ª Æ º łŁ . ˇ æ æ V
æ ø æ ºŁ Ø ŁæŁ ß æŁæ ß Œ æ Œ ŒŁ ª Æ º łŁ Łæº Łı Œ .
˛ º Ł 8.2.1. ¸Ł Ø æ æ V
ß æ Œ ß , æºŁ æ ø æ º Łæº N
Œ , Łæº ºŁ Ø
ŁæŁ ßı Œ º Æ Ø æŁæ æ æ V
æı Ł N
. ´ Ł æº , ºŁ Ø æ æ V
ß æ Æ æŒ ß .
ˇ Ł
:
1. V
= k
n
Œ ºŁ Ø æ æ .
2. V
= k
[x
]
Æ æŒ ºŁ Ø æ æ .
8.2. ` Łæ ºŁ Ø ª æ æ
´ Œ ßı ºŁ Ø ßı æ æ ı ª Ł Æ Łæ
Œ Œ Œ Ø, Œ Ł Æ æŒ Ø æŁæ ß Œ . ´ æ æ Ł,
ª Ł Æ Łæ æ ª Œ ª ºŁ Ø ª æ æ V
.
| ˛ º Ł 8.2.2. ` Łæ
|
º ª Œ
|
ª
|
æ æ
|
| V
ß æ ºŁ
|
Ø ŁæŁ
|
æŁæ
|
Œ
|
| B
= {e
1
,e
2
,...,en
}, º
æº ŁØ:
|
º Æ Ł æº
|
øŁı
|
æŁº
|
ßı
|
| 1. º Æ Ø Œ a
∈ V
ºŁ Ø
|
ß æ
|
æŁæ
|
B
;
|
| 2. ∀ a
∈ V
æŁæ (B,a
)
|
º æ ºŁ Ø
|
ŁæŁ Ø;
|
| 3. æ æ V
æ ø æ
|
ºŁ Ø
|
ŁæŁ ßı
|
æŁæ
|
æ
|
| Łæº Œ Æ º łŁ ,
|
B
.
|
˛ º Ł 8.2.3. — æ º ª ºŁ Ø ª æ æ æ Ł æ Łæº 0. — æ º ª Œ ª ºŁ Ø ª æ æ V
ß æ Łæº Œ º Æ Æ Łæ ª -
æ æ ŁºŁ ŒæŁ º Łæº ºŁ Ø ŁæŁ ßı Œ ª æ æ V
.
— æ Œ ª ºŁ Ø ª æ æ V
Æ Æ dim V
ŁºŁ rang V
.
ˇ Ł
:
1. dim
{0} = 0;
2. dim kn
= n
;
3. dim M
(m
× n,k
) = mn
;
4. dim L
= n
− r
;
5. dim
{f
(x
) ∈ k
[x
]|deg f
(x
) 6 n
} = n
+ 1.
ˇ æ V
Œ ºŁ Ø æ æ Ł e
1
,e
2
,...,en
ª Æ Łæ. ª º Æ Ø Œ a
∈ V
ß Ł Æ Łæ
a
= α
1
e
1
+ α
2
e
2
+ ...
+ αn
en
.
(8.1)
Œ Œ Œ Æ Łæ º æ ºŁ Ø ŁæŁ Ø æŁæ Ø Œ , ß Ł (8.1) º Œ a
Ł æ . ŒŁ Æ , Œ -
Πa
∈ V
æ Ł æ æ æ Ł æŁæ
(α
1
,α
2
,...,αn
) æŁ º Æ Łæ e
1
,e
2
,...,en
.
˛ º Ł 8.2.4. ˚ Ł Ł (Œ Ł) Œ a
∈ V
æŁ º ª Æ Łæ e
1
,e
2
,...,en
ºŁ Ø ª æ æ V
ß æ æ Œ æ Œ Ł Ł ºŁ Ø ª ß Ł Œ a
Æ Łæ.
ˇŁł , Œ a
= (α
1
,α
2
,...,αn
).
| ˛
|
º Ł 8.2.5. ˚ Ł
|
ß
|
æ ºÆ Œ a
æŁ º
|
| ª
|
Æ Łæ e
1
,e
2
,...,en
|
ß
|
æ æ ºÆ , æ æ º ßØ Ł Œ -
|
| Ł
|
Πa
æŁ º
|
ª
|
Æ Łæ .
|
| ˛Æ
|
α
1
α
2
Ł a
ˇ = .
...
αn
|
| ˛
|
º
|
Ł 8.2.6. æ
|
º Ł
|
Πa
∈ V
ª Œ Ł -
|
| ª æ
|
ºÆ
|
æŁ º
|
ª Æ
|
Łæ æ æ V
ß æ
|
| æ
|
ß Æ Ł ºŁ
|
Ø ª
|
æ æ V
æ Ł n
|
| Œ
|
Ł
|
ºŁ Ø æ
|
æ
|
k
n
.
|
| æ
|
,
|
Œ ßØ Æ Łæ e
1
,e
2
,...,en
º æ æ
|
Æ Ł V
→ kn
.
8.3. ¨ Ł ºŁ Ø ßı æ æ
ˇ º Ł 8.2.1. ˚ Ł ßØ æ ºÆ æ ß ı Œ æ Œ Ł ßı æ ºÆ æº ª ßı Œ . ˚ Ł ßØ æ ºÆ Ł Ł Œ æŒ º , Œ Ł æ ºÆ-
ª Œ , æŒ º .
º Ł 8.2.1 , a
+ˇ b
= a
ˇ +ˇb
Ł αa
ˇ = αa
ˇ.
˜ Ł ª ŁæŁ (8.1). æ , a
ˇ>
= (α
1
,α
2
,...,αn
)
Ł æ Ł 1×n
. — ææ Ł Æ Łæ ßØ æ ºÆ æ æ
 Ł æ Ł n
×1. ª a
ˇ>
e
˜ = α
1
e
1
+α
2
e
2
+ Ł æ Ł n
×1. ª a
ˇ>
e
˜ = α
1
e
1
+α
2
e
2
+
. ŒŁ Æ , a
= a
ˇ>
e
˜ Ł Łæ æ
8.3 ¨ Ł ºŁ Ø ßı æ æ
ˇ æ V
Ł V
0
ºŁ Ø ßı æ æ Ł Ł æ ß º k
.
˛ º Ł 8.3.1. ¨ Ł ºŁ Ø ª æ æ V
ºŁ-
Ø æ æ V
0
Ł Ł æ ß º k
ß æ æ Œ ÆŁ Œ Ł f
: V
→ V
0
, º ø æº Ł ºŁ Ø æ Ł:
1. (∀ a,b
∈ V
) f
(a
+ b
) = f
(a
) + f
(b
);
2. (∀ α
∈ k, a
∈ V
) f
(αa
) = αf
(a
).
æº Ł 1 , Æ Ł f
º æ Ł Ł -
Ł Ł Ø ª ß (V,
+)
Ł Ł ª 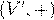 . .
˛ º Ł 8.3.2. ¸Ł Ø æ æ V
ß æ Ł ß ºŁ Ø æ æ V
0
(V
∼
= V
0
), æºŁ æ ø æ ı Æß
Ł Ł Ł f
: V
→ V
0
.
ˇ º Ł 8.3.1. ˛ ł Ł Ł Ł º æ ł Ł
Œ Ł º æ Ł Œº ææ ºŁ Ø ßı æ æ Ł Ł æ ß º k
.
º Ł 8.3.1 , º ł Ł Ł æ Ł
| æ ºŁ ß æº
|
øŁ
|
Ł
|
| 1. V
∼
=
V
, æ
|
ß º æ
|
æ Øæ
|
º ŒæŁ
|
æ Ł;
|
| 2. æºŁ V
∼= V
0,
|
V
0 ∼= V
(æŁ
|
Ł
|
æ
|
);
|
3. æºŁ V
00 ∼= V
0 Ł V
0 ∼= V
, V
00 ∼= V
( Ł Ł æ ).
¯˛—¯ 8.3.1 ( æ Øæ ı Ł ßı ºŁ Ø ßı æ æ ). ºŁ ß æº øŁ Ł :
1. Ł Ł Ł ºŁ Ø ŁæŁ Ø æŁæ ß Œ ı
ºŁ Ø ŁæŁ ß , ºŁ Ø ŁæŁ ß æŁæ ß Œ
| ı
|
ºŁ Ø
|
ŁæŁ ß ;
|
| 2. Ł
|
ß
|
ºŁ Ø ß
|
æ æ
|
ºŁÆ
|
Œ
|
-
|
| ß , ºŁÆ
|
Æ æŒ
|
ß ;
|
3. Ł Ł Ł Æ Łæ æŁæ ß Œ ı Ł Æ Łæ, ª æŁæ ß Œ Ł Ł Ł Ł æ .
˜ Œ º æ . 1) ˇ æ f
: V
→ V
0
º æ Ł Ł . ´ -
ºŁ Ø ŁæŁ æŁæ Œ a
1
,a
2
,...,as
Ł V
. , æ ø æ æŒ º ß α
1
,α
2
,...,αs
æ ß º ŒŁ , α
1
a
1
+ α
2
a
2
+ ...
+ αs
as
= 0. ˇ Ø Œ Æ Łı Œ -
f
(α
1
a
1
+ α
2
a
2
+ ...
+ αs
as
) = f
(0). ΠΠΠf
Ł Ł ,
α
1
f
(a
1
) + α
2
f
(a
2
) + ...
+ αs
f
(as
) = 0, æ æ αi
= 0. ˇ æº æ ł Ł Œ ß , Œ ß f
(a
1
),f
(a
2
),...,f
(as
) º æ ºŁ Ø ŁæŁ ß Ł V
0
.
8.3. ¨ Ł ºŁ Ø ßı æ æ ˇ æ a
1
,a
2
,...,as
ºŁ Ø ŁæŁ æŁæ Œ Ł V
. ˝
Π, f
(a
1
),f
(a
2
),...,f
(as
) Œ º æ ºŁ Ø ŁæŁ-
Ø. ˜ æ Ł Ł , æ æŁæ f
(a
1
),f
(a
2
),...,f
(as
) º æ ºŁ Ø ŁæŁ Ø. ª ææ Ł Æ Ł f
−1
: V
0
→ V
,
Œ Œ º æ Ł Ł . ˇ Ł Æ ŁŁ ºŁ Ø-
ŁæŁ ß Œ ß f
(a
1
),f
(a
2
),...,f
(as
) Ø ºŁ Ø ŁæŁß Œ ß a
1
,a
2
,...,as
, Ł Ł ºŁ Ø Ø ŁæŁ æ Ł
a
1
,a
2
,...,as
.
2) ˇ æ f
: V
→ V
0
Ł V
º æ Œ ß ºŁ Ø ß æ æ . , æ ø æ º Łæº N
Π,
| Łæº
|
Œ º Æ Ø ºŁ Ø ŁæŁ Ø æŁæ ß Ł
|
æ -
|
| æ V
|
æı Ł ª Łæº N
. Œ Œ Œ Ł Ł Ł
|
º Œ
|
| ºŁ Ø
|
ŁæŁ æŁæ Œ ı Ł ºŁ Ø
|
Ł-
|
| æŁ ,
|
æ æ V
0
Łæº Œ º Æ Ø ºŁ Ø
|
Ł-
|
| æŁ Ø æŁæ
|
Œ Æ ª Ł Ł Łæº N
, æº
|
º
|
| æ æ
|
V
0
Æ Œ ß .
|
| ˇ æ V
|
º æ Æ æŒ ß ºŁ Ø ß æ æ
|
. ˝
|
Œ , Ł V
0
æº Œ Æ Æ æŒ ß . ˜ æ Ł Ł , æ V
0
º æ Œ ß ºŁ Ø ß -
æ æ . ª ææ Ł Ł Ł f
−1
: V
0
→ V
. ˇ Ł
Ł Ł Ł Œ æ Ł V
0
Æ æº Œ æ
V
, Ł Ł æº Ł .
3) ˇ æ A
æŁæ Œ Ł V
, B
Æ Łæ æŁæ ß Œ A
Ł
f
: V
→ V
0
Ł Ł . ª , Œ Œ Œ B
⊂ A
, f
(B
) ⊂ f
(A
). ˜ º ,
A
ºŁ Ø ß æ B
, ª f
(A
)
Æ ºŁ Ø ß æ f
(B
)
. ˝ Œ , Œ Œ Œ B
ºŁ Ø ŁæŁ æŁæ Œ -
, f
(B
)
Œ º æ ºŁ Ø ŁæŁ Ø. ŒŁ Æ , f
(B
)
º æ Æ Łæ f
(A
)
, æ Æ Łæ B
æŁæ ß Œ A
ı Ł
Æ Łæ f
(B
)
æŁæ ß Œ f
(A
)
. ΠΠΠf
º æ ÆŁ Œ Ł Ø, Łæº Œ B
Łæº Œ f
(B
), æ r
(A
) = r
(f
(A
)). 
º æ Ł
8.3.1.1.
¨ ß Œ ß ºŁ Ø ß æ æ
Ł Ł Œ æ .
˜ Œ º æ . ˜ Øæ Ł º , f
: V
→ V
0
Ł Ł Ł V
Ł V
0
º æ Œ ß Ł ºŁ Ø ß Ł æ æ Ł. ª Æ Łæ
e
1
,e
2
,...,en
æ æ V
ı Ł Æ Łæ f
(e
1
),f
(e
2
),...,f
(en
) æ æ V
0
, æ dim V
= n
= dim V
0
. 
| ¯˛—¯ 8.3.2. ¸ Æ Œ ºŁ Ø
|
æ æ V
|
| æ Ł n
Ł
|
Œ Ł ºŁ Ø
|
æ æ kn
|
| Ł Ł Ł Ł
|
æ Łª æ æ ø
|
æ
|
ª Æ-
|
| Ł f
: V
→ kn
|
æŁ º º Æ ª Æ Łæ
|
æ
|
æ V
.
|
| ˜ Œ º æ . ˇ æ
|
e
1
e
2 dim V
= n
Ł e
˜ =
...
en
|
Æ
|
Łæ V
. — ææ -
|
| Ł æ Æ
|
Ł f
: V
→ kn
. ¨ æ
|
,
|
æºŁ a
= a
ˇ>
e
˜,
|
| f
(a
) = a
ˇ. ˇ Œ ,
|
Æ Ł f
º
|
æ
|
Ł Ł .
|
| ´ - ßı, f
º æ
a
ˇ = ˇb
⇒ a
= b
.
|
Ł œ Œ Ł Ø. ˜ Øæ Ł º
|
, æºŁ f
(a
) = f
(b
),
|
| ´ - ßı, f
º æ æ œ Œ Ł Ø. ´ æ
|
º , º Æ Ø
|
æ ºÆ a
ˇ ∈ kn
Ł æ Ł Œ a
= a
ˇ>
e
˜. ª f
(a
) = a
ˇ.
˛æ æ Œ , Æ Ł f
æ ı ŁŁ. — ææ -
Ł f
(a
+ b
) = a
+ˇ b
= a
ˇ + ˇb
= f
(a
) + f
(b
). f
(αa
) = αa
ˇ = αa
ˇ = αf
(a
).
ŒŁ Æ f
: V
→ k
n
º æ Ł Ł , æº º
V
∼
= kn
. 
º æ Ł
8.3.2.1.
˚ ß ºŁ Ø ß æ æ Ł Œ Ø æ Ł Ł ß.
8.4. ˇ ı ª Æ Łæ Œ ª . Ł ı
˜ Œ º æ . ˜ Øæ Ł º , æ æ dim V
= n
Ł dim V
0
= n
. ª 8.3.2 V
∼
=
kn
Ł V
0
∼
=
kn
, æº º -
V
∼
= V
0
. 
| º æ Ł
8.3.2.2.
— ª æŁæ ß Œ Œ
|
ª ºŁ Ø
|
ª
|
| æ æ V
ª æŁæ ß Œ Ł
|
ßı æ
|
ºÆ Œ
|
| Ø æŁæ ß æŁ º º Æ ª Æ Łæ æ
|
æ
|
V
.
|
| ˜ Œ º æ . ˇ æ a
1
,a
2
,...,as
æŁæ
|
Œ
|
Ł V
. — ææ
|
-
|
| Ł f
: V
→ k
n
æ ßØ Ł Ł
|
, ª
|
æŁæ Œ
|
-
|
| a
1
,a
2
,...,as
ı Ł a
ˇ1
,a
ˇ2
,...,a
ˇs
. ˝
|
Ł 3
|
-
|
ß 8.3.1 r
(a
1,a
2,...,a
s
) = r
(a
ˇ1,a
ˇ2,...,a
ˇs
). 
8.4 ˇ ı ª Æ Łæ Œ ª . Ł ı
ˇ æ V
Œ ºŁ Ø æ æ k
, dim V
= n
Ł æ
e
1
u
1
e
2
u
2 e
= Ł u
e = ...
e ...
en
un
Æ Łæ æ æ V
. ´ß Ł Œ ß Æ Łæ u
e
Œ ß
 Łæ e
e: Łæ e
e:
| u
1 = α
11e
1 + α
21e
2 + ...
+ α
n
1e
n
;
|
| u
2 = α
12e
1 + α
22e
2 + ...
+ α
n
2e
n
;
...
u
n
= α
1n
e
1 + α
2n
e
2 + ...
+ α
nn
e
n
.
|
(8.2)
|
˛ º Ł 8.4.1. Ł Ø ı Æ Łæ e
e
Œ Æ Łæ u
e
ß æ Ł , æ Ł Œ Ł , æ æ º Ø Ł Œ Ł-
Ł ºŁ Ø ª ß Ł Œ Łæ u
e Œ ß Æ Łæ Łæ u
e Œ ß Æ Łæ
| e
.
e
|
| ˛
|
º Ł 8.4.1 , Ł ı
>
α
11 α
21 ... α
n
1 α
11 α
12 ... α
1n
α
12 α
22 ... α
n
2 α
21 α
22 ... α
2n
Q
= = .
... ... ... ...
... ... ... ...
α
1n
α
2n
... α
nn
α
n
1 α
n
2 ... α
nn
|
| ˇ ß
|
æ ºÆ Ł ß º æ Œ Ł ßØ æ ºÆ Œ
|
u
1
.
|
| ´ ß
|
Œ Ł ßØ æ ºÆ Œ u
2
, Ł . .
|
| ˛
|
º Ł 8.4.2. Ł Ø ı Æ Łæ e
e
Œ Æ Łæ
|
u
ß-
e
|
| æ
|
Ł Q
, æ ºÆ Ł Œ Ø º æ Œ Ł ß æ ºÆ ß
|
| Œ
|
Æ Łæ u
e
æŁ º Æ Łæ e
e
, æ
|
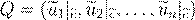 . .
| ˛ º Ł 8.4.3. Ł
|
Ø
|
ı
|
Æ Łæ e
e
Œ Æ Łæ u
e
ß -
|
| æ Ł Q
, º æŁæ ß (8.2).
|
æ
|
u
= Q
>
e
e e
|
Ł Łæ
|
| ¯˛—¯ 8.4.1 (
Ł
|
Ł
|
ı
|
).
|
ºŁ ß æº øŁ
|
| 1. Ł ı
|
ª
|
Æ Łæ
|
Œ ª
|
º æ æ -
|
| Æ Ø. ˛Æ , º Æ
|
æ Æ
|
Ł
|
ææ -
|
| Ł Œ Œ Ł
ª Æ Łæ .
|
ı
|
ª Æ
|
Łæ Œ Œ
|
| 2. Ł ß ı Æ
|
Łæ
|
e
Œ Æ e
|
Łæ u
Ł e
|
Æ Łæ u
Œ Æ Łæ e
e e
|
| º æ Ł Æ
|
ß Ł.
|
| ˜ Œ º æ . 1) ˇ æ Q
º Æ
|
æ Æ
|
Ł Ł e
e
-
|
| ßØ Æ Łæ æ æ V
. ˇ æ Ł
|
Œ ß u
1
,u
2
,...,un
ŒŁ
|
| 8.4. ˇ ı ª Æ
|
Łæ Œ ª
|
. Ł
|
ı
|
| Æ , Æß Łı Œ
|
Ł ß æ
|
ºÆ ß
|
æŁ
|
º
|
Æ
|
Łæ
|
e
æ e
|
-
|
| ºŁ æ æ ºÆ Ł
|
Ł ß Q
.
|
| ΠΠΠ|Q
| 6= 0,
|
æ ºÆ ß
|
Ł ß Q
|
º
|
æ
|
ºŁ
|
Ø
|
Ł-
|
æŁ ß Ł, Ł Œ ß u
1,u
2,...,u
n
Æ ºŁ Ø ŁæŁ ß Ł.
´ æŁº ª , Œ ß u
1
,u
2
,...,un
Œ æ Æ Łæ u
e
æ æ V
.
ˇ æ Ł Æ Ł u
e
= Q
>
e
e
, æ Ł Q
º æ Ł Ø ı ª Æ Łæ e
e
Œ æ Æ Łæ
u
e
.
2) ˇ æ  Ł Æ Łæ æ æ V
. ˇ æ Q
Ł ı e
e
Πu
e
, R
Ł ı Ł Æ Łæ æ æ V
. ˇ æ Q
Ł ı e
e
Πu
e
, R
Ł ı 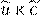 . ª º Ł 8.4.3 Æ . ª º Ł 8.4.3 Æ
Ł u
e
= Q
>
e
e
, e
e
= R
>
u
e
. ˛ æ , e
e
= R
>
(Q
>
e
e
) = (R
>
Q
>
)e
e
= (QR
)>
e
e
.
| æ Œ
|
ß
|
,
|
Ł
|
QR
º æ
|
Ł Ø
|
| ı e
e
Πe
e
. ˝
|
Ø
|
Ł Ø
|
º
|
æ
|
Ł E
, æº
|
º
|
| QR
= E
. æ
|
ł Ł
|
Œ
|
ß
|
,
|
Q
Ł R
|
æ Æ
|
ß
|
Ł Æ ß Ł ß, æ Q
= R
−1
. 
| ¯˛—¯ 8.4.2. ˚
|
Ł
|
ßØ æ
|
ºÆ
|
Œ
|
æŁ º
|
-
|
| ª Æ Łæ Œ Ł
|
æ
|
ºÆ
|
ª
|
Œ
|
æŁ
|
º
|
| æ ª Æ Łæ ,
Łæ Œ æ , æ
|
æº
|
Ł
|
ı
|
ª Æ -
|
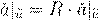 , ,
| ª R
|
Ł
|
ı
|
Æ
|
Łæ u
Œ Æ Łæ e
|
e
. e
|
| ˜ Œ
|
º æ
|
. ˇ æ e
e
|
æ
|
ßØ Æ Łæ, u
e
|
ßØ Æ
|
Łæ, R
-
|
| Ł
|
ı
|
u
Πe
e
, e
|
æ
|
e
= R
>
u
. e e
|
Ø æ
|
ß, Œ
|
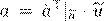 . ª Ø æ ß, Œ . ª Ø æ ß, Œ 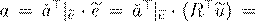
| (a
ˇ>
|e
e· R
>
)u
e
= (R
· a
ˇ|e
e)>
u
e
.
|
| Œ Œ Œ ß Ł Œ
|
a
|
Æ
|
Łæ u
e
|
º æ
|
Ł æ
|
ß ,
|
a
ˇ>
|u
e
= (R
·a
ˇ|e
e)>
. æ Ł Ł Ł ß, º Ł a
ˇ|u
e = R
·a
ˇ|e
e. 
8.5 ¸Ł Ø ß æ æ
ˇ æ V
ºŁ Ø æ æ º k
.
˛ º Ł 8.5.1. ˇ æ L
Æ Łæ ª æ V
ß æ æ Ø Ł ß æ , æºŁ æ Ø Ł æŁ º -
ª æº Ł Ł ł ª Ł , æ
1. (∀ a,b
∈ L
) a
+ b
∈ L
;
2. (∀ α
∈ k, a
∈ L
) αa
∈ L
.
º æ Ł . æ Ø Ł æ L
, ææ æ æ Ł Ł ß Ł Ł Ł, Æ ºŁ Ø æ æ .
˜ Œ º æ . L
⊂ V
Ł L
æ Ø Ł æ , ª L
ææ Ł Ł ß ŁŁ ª æº Ł Ł
ł ª Ł . ˇ Œ , (∀ a,b
∈ L
) a
− b
∈ L
. ˜ Øæ Ł-
º , −b
= −(1 · b
) = (−1)b
∈ L
, ª a
− b
= a
+ (−b
) ∈ L
. ŒŁ
Æ , (L,
+) Æ Ł Ł ª ª ß (V,
+). ˇ ß Ł ŒæŁ ß ºŁ Ø ª æ æ ß º æ L
, æ º -
ß ß ŒæŁ ß, æ øŁ æ Œ ł Ł , ß º æ æ æ V
, Æ ß º æ Ł æ Ø Ł æ L
. Ł æ º , L
º æ ºŁ Ø ß æ æ . 
˛ º Ł 8.5.2. ¸Ł Ø ß æ æ æ æ V
ß æ æ Œ ª æ Ø Ł æ L
, ææ æ
æ Ł Ł ß Ł Ł Ł.
ˇ º Ł 8.5.1. ˇ æ Ł æ Øæ ºŁ Ø ßı -
æ æ ºŁ Ø ª æ æ V
æ º æ æ æ æ æ V
.
| ˜ Œ
|
º æ
|
. ´ æ
|
º , æ
|
{Li
}
|
æ
|
Øæ
|
ºŁ
|
Ø ßı
|
-
|
| æ
|
æ
|
æ æ
|
V
. — ææ
|
Ł
|
æ
|
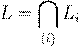 . .
| ˝
|
Π, L
æ
|
Ø Ł
|
æ
|
æ
|
æ
|
V
.
|
| ˇ æ
|
a,b
∈ L
⇒ (∀ i
)
|
a,b
∈ Li
.
|
ΠΠΠLi
|
ºŁ Ø
|
-
|
æ æ , 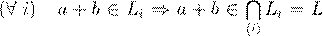 . º º , L . º º , L
| æ
|
Ø Ł
|
æŁ º
|
ª æº Ł .
|
| º ªŁ
|
Œ ß
|
æ ,
|
(∀ α
∈ k,a
∈ L
)
|
αa
∈ L
.
|
º º , L
æ æ æ æ V
. 
| ˇ æ
|
A
|
æ ºŁ
|
Ø ª
|
æ æ V
. — ææ
|
-
|
| Ł æ ºŁ
|
Ø ß
|
æ
|
æ L
|
æ
|
æ
|
V
, æ øŁ
|
-
|
| æ A
.
|
ŒŁ
|
æ
|
æ æ ø æ
|
,
|
Ł , æ æ
|
| V
. æ Ł
|
æ
|
Ł æ ı
|
Łı
|
æ
|
æ
|
L
, æ
|
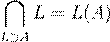 . .
| ˇ º
|
Ł
|
8.5.2. æ L
(A
)
|
Ł
|
ł
|
ºŁ Ø
|
-
|
| æ
|
æ
|
æ æ V
, æ ø
|
æ
|
A
.
|
| ˜ Œ
|
º æ
|
. ˜ Øæ Ł º , Œ ,
|
L
(A
)
|
º æ
|
-
|
æ æ æ æ V
æº Ł º Ł 8.5.1. ˜ º , æ A
æ Ł æ æ ı L
Œ ß ß æ Œ , æº º
A
⊂ L
(A
).
˝ Œ , º Æ ºŁ Ø æ æ L
0
, Π, A
⊂ L
0
. ª ı Ł æ æ Ł æ Œ ßı æ æ L
,
æº º L
(A
) ⊂ L
0
. 
˛ º Ł 8.5.3. ¸Ł Ø Ø Æ º Œ Ø æ A
æ æ V
ß æ Ł ł ºŁ Ø æ æ L
(A
)
æ æ V
, æ ø æ A
.
æ ª , æ æ L
(A
)
æ A
ŁºŁ æ A
.
| ˇ º Ł 8.5.3 (æ
|
Ł L
(A
)). ¸Ł Ø
|
Æ º
|
ΠL
(A
) æ -
|
| æ Ł Ł æ ºŁ
|
Ø ßı Œ ÆŁ ŁØ Œ
|
ßı
|
æ
|
| æ A
æ Œ Ł Ł
|
Ł Ł æ ª
|
º
|
k
,
|
æ
|
 ) )
Ł Ł æ αa
= 0 .
˜ Œ º æ . ´ æ º , Æ Ł : 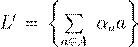 . .
˝ Æı Ł Œ , L
(A
) = L
0
.
Ø æ ß, Œ Œ Œ A
⊂ L
(A
)
, L
(A
)
æ Ł º Æ ºŁ-
Ø Œ ÆŁ Ł Œ ª æ æ Œ A
,
æ L
0
⊂ L
(A
).
ª Ø æ ß, æ , L
0
æ Ø Ł æ æ æ V
, æº º , L
0
ºŁ Ø æ æ æ æ V
.
˚ ª , æ A
⊂ L
0
( ΠΠΠa
= 1 · a
+ 0 · a
1
+ 0 · a
2
+ ...
).
ª º Ł 8.5.2 L
(A
) ⊂ L
0
.
´ Ł ª º , L
(A
) = L
0
. 
º æ Ł 8.5.0.1. ¯æºŁ A
= {a
1
,a
2
,...,as
}, ª Œ ß a
1
,a
2
,...,as
º æ ºŁ Ø ŁæŁ ß Ł, L
(A
) Π, dim L
(A
) =
= s
Ł
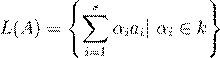 . .
˜ Œ º æ . ˜ Øæ Ł º , Œ , L
(A
) Ł Œ ßØ
Ł æº Ł º Ł 8.5.3. ª Œ ß a
1
,a
2
,...,as
Œ æ Æ Łæ L
(A
), æº º , dim L
(A
) = s
. 
º æ Ł
8.5.0.2.
¯æºŁ ºŁ Ø æ æ V
Œ , º Æ ª ºŁ Ø æ æ L
Œ º æ Œ ß Ł
dim L
6 dim V
. ¯æºŁ dim L
= dim V
, L
= V
.
˜ Œ º æ . ´ æ º , æ dim V
= n
Ł e
1
,e
2
,...,en
Æ -
Łæ V
. ΠΠΠL
æ æ ºŁ Ø ª æ æ V
,
º Æß Œ ß . ´ Ł æº , Ł Æ æŒ -
æ Ł æ æ L
ß Œ º Æß Æ æŒ æ æ æ V
.
ˇ æ a
1
,a
2
,...,as
Æ Łæ L
, æ dim L
= s
. ΠΠΠa
1
,a
2
,...,as
ºŁ Ø ß æ Æ Łæ e
1
,e
2
,...,en
æ æ V
, æØ ºŁ Ø Ø ŁæŁ æ Ł s
6 n
, æ dim L
6 dim V
.
¯æºŁ dim L
= dim V
, æ s
= n
, Œ ß a
1
,a
2
,...,an
Œ æ Æ Łæ æ æ V
. ´ æŁº º Ł 8.5.3 Æ
Ł
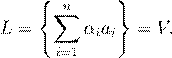

˛ º Ł 8.5.4. Ø æ Øæ ºŁ Ø ßı æ æ {L
i
}
æ æ V
ß æ ºŁ Ø Æ º Œ æ ,
ŁŒ - æ Æœ Ł Ł Æ Łæ ßı æ Łı ºŁØ ßı æ æ , æ
.
 ˛ º Ł 8.5.5. Ø æ Øæ ºŁ Ø ßı æ æ {L
i
}
æ æ V
ß æ Ł ł ºŁ Ø æ æ - ˛ º Ł 8.5.5. Ø æ Øæ ºŁ Ø ßı æ æ {L
i
}
æ æ V
ß æ Ł ł ºŁ Ø æ æ -
æ æ V
, æ ø æ æ æ ª æ Øæ .
ˇ º Ł 8.5.4 (æ Ł æ ß). L
1
+ L
2
ı ºŁ-
Ø ßı æ æ æ æ æ Œ Ł
{a
1
+ a
2
| a
1
∈ L
1
,a
2
∈ L
2
}.
˜ Œ º æ . ˜ Øæ Ł º , º Ł 8.5.4 Ł L
1
+L
2
=
= L
(L
1
∪ L
2
). ´ Æ Ł L
0
= {a
1
+ a
2
| ai
∈ Li
, i
= 1,
2}. ˝ Œ , L
1
+ L
2
= L
0
.
Ø æ ß, æ , L
0
æ Ø Ł æ æ æ V
, L
0
ºŁ Ø æ æ æ æ V
.
˜ º , L
1
⊂ L
0
. ˜ Øæ Ł º , (∀ a
1
∈ L
1
) a
1
= a
1
+ 0, ª 0 ∈ L
2
.
º ªŁ , L
2
⊂ L
0
, Ł (∀ a
2
∈ L
2
) a
2
= 0+a
2
, ª 0 ∈ L
1
. ˛ æ ,
L
1
∪ L
2
⊂ L
0
, æº º L
(L
1
∪ L
2
) ⊂ L
0
, æ L
1
+ L
2
⊂ L
0
.
ª Ø æ ß, Ł º ßØ Œ a
∈ L
0
. ¯ª
æ Ł Ł a
= a
1
+ a
2
, ª a
1
∈ L
1
, a
2
∈ L
2
. ´ Œ ß a
1
,a
2
∈
| ∈ L
1
∪ L
2
, æº
|
º a
= a
1
+ a
2
∈ L
(L
1
∪ L
2
) = L
1
+ L
2
,
|
æ
|
| a
∈ L
1
+ L
2
. ¨
|
L
0
⊂ L
1
+ L
2
.
|
ŒŁ Æ , Ł ı Œº ŁØ º , L
1
+ L
2
= L
0
. 
| ˙
|
Ł 8.5.1.
Œ , Æø
|
æº
|
|
X X Ł Ł
L
i
= a
i
| a
i
∈ L
i
(i
) (i
)
|
æ
|
ai
= 0 .
|
| ˛
|
º Ł 8.5.6. ºŁ Ø ßı
|
æ
|
æ L
1
+L
2
ß -
|
| æ
|
Ø, æºŁ L
1
∩ L
2
= {0}.
|
| ˇ
|
æ Æ æ L
1
⊕ L
2
.
|
| ¸
|
8.5.1. ¸ Æ ºŁ Ø ŁæŁ
|
æŁæ
|
ΠΠ-
|
| ª ºŁ Ø ª æ æ V
|
º Ł Æ Łæ -
|
| æ
|
æ
|
V
.
|
| ˜ Œ
|
º æ . ˇ æ a
1
,a
2
,...,as
ºŁ
|
Ø
|
ŁæŁ æŁæ
|
| Œ
|
Ł V
Ł e
1
,e
2
,...,en
Æ Łæ æ
|
æ
|
V
, dim V
= n
. — æ-
|
| æ
|
Ł
|
æº ø æŁæ Œ
|
| a
1
,a
2
,...,as
,e
1
,e
2
,...,en
.
|
(8.3)
|
| ¨
|
Ø æŁæ ß Œ (8.3) º
|
Œ ß, Œ ß ºŁ-
|
| Ø
|
ß æ ß øŁ . ˇ ß s
|
Œ æ æ
|
| æ
|
, Œ Œ Œ Ł ºŁ Ø ŁæŁ ß . ˇ º Ł
|
| a
1
,a
2
,...,as
,ei
1
,ei
2
,...,ei
k
.
|
(8.4)
|
Łæ Œ (8.4) Æ ºŁ Ø ŁæŁ Ø, Œ Œ Œ Ł Ł Œß æ æ º ß Œ ß.
˜ º , º Æ Ø Œ a
∈ V
, ºŁ Ø ß æ æŁæ (8.3),
Æ ºŁ Ø ß æ Ł æŁæ (8.4), Œ Œ Œ º ß Œß Ł æŁæ ß (8.3), ºŁ Ø ß æ æŁæ (8.4). ŒŁ
Æ , æŁæ Œ (8.4) Æ æ æ º Æ Łæ æ æ V
.
Æ Łæ º Ł æŁæ ß a
1
,a
2
,...,as
Æ º Ł Œ ßı Œ. k
= n
− s
. 
¯˛—¯ 8.5.1 ( æ Ł æ ß ı ºŁ Ø ßı æ æ ). — æ æ ß ı ºŁ Ø ßı æ æ Œ -
ª ºŁ Ø ª æ æ V
æ æ Ø Łı
ºŁ Ø ßı æ æ Æ æ Ł Łı æ Ł , æ
dim
(L
1
+ L
2
) = dim L
1
+ dim L
2
− dim
(L
1
∩ L
2
).
| ˜ Œ º æ . ˇ æ L
1
Ł L
2
ºŁ Ø ßı
|
æ
|
æ
|
-
|
| æ
|
æ V
. ˛Æ Ł L
= L
1
∩ L
2
. ˇ æ
|
æŁæ
|
Œ
|
| e
1
,e
2
,...,er
|
(8.5)
|
| Æ Łæ L
. ¯æºŁ L
= {0}, r
= 0 Ł Æ Łæ Æ
|
æ
|
æ .
|
| ˇ
|
º Æ Łæ L
º Ł Æ Łæ L
1
|
| e
1
,e
2
,...,er
,ur
+1
,...,us
,
|
(8.6)
|
| ª
|
(8.6) Æ Łæ L
1
, dim L
1
= s
. º ªŁ ,
º Ł Æ Łæ L
2
|
º
|
Æ
|
Łæ L
|
| e
1
,e
2
,...,er
,vr
+1
,...,vt
,
|
(8.7)
|
| ª
|
(8.7) Æ Łæ L
2
, dim L
2
= t
.
— ææ Ł æº ø æŁæ Œ
|
e
1
,e
2
,...,er
,ur
+1
,...,us
,vr
+1
,...,vt
.
(8.8)
ˇ Œ æŁæ (8.8) º æ Æ Łæ L
1
+ L
2
. ˜ Øæ Ł º ,
Ł º ßØ Œ x
∈ L
1
+ L
2
. ª x
= a
+ b
, ª a
∈ L
1
, b
∈ L
2
. — º ª Œ a
Æ Łæ (8.6), Œ b
Æ Łæ (8.7) Ł
挺 ß º ß ß Ł , ß º Ł , Œ x
ºŁ Ø ß æ æŁæ (8.8).
˛æ æ Œ , æŁæ Œ (8.8) º æ ºŁ Ø -
ŁæŁ Ø. — ææ Ł ºŁ Ø Œ ÆŁ Ł
α
1e
1 +...
+α
r
e
r
+β
r
+1u
r
+1 +...
+β
s
u
s
+γ
r
+1v
r
+1 +...
+γ
t
v
t
= 0.
(8.9)
˝ Œ , æ æŒ º ß α
i
,β
i
,γ
i
= 0. — ææ Ł Œ
x
= α
1
e
1
+ ...
+ αr
er
+ βr
+1
ur
+1
+ ...
+ βs
us
.
(8.10)
¨ æ (8.9) Ł , Œ
x
= −γr
+1
vr
+1
− ...
− γt
vt
.
(8.11)
— æ (8.10) Œ ß , Œ x
∈ L
1
, æ (8.11)
Œ ß , Œ x
∈ L
2
, æº º x
∈ L
1
∩ L
2
= L
.
º º , Œ x
ß Ł Æ Łæ L
.
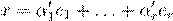 .
(8.12) .
(8.12)
Ł (8.10) Ł (8.12). ´ß Ł Œ x
Æ Łæ (8.6) º
Æß Ł æ ß , ª
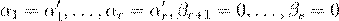 . .
ª æ (8.9) Ł Ł Ł
α
1
e
1
+ ...
+ αr
er
+ γr
+1
vr
+1
+ ...
+ γt
vt
= 0.
(8.13)
Œ Œ Œ Æ Łæ (8.7) º æ ºŁ Ø ŁæŁ Ø æŁæ Ø Œ ,
Ł æ (8.13) æº , æ æŒ º ß α
1
= ...
= αr
= γr
+1
=
= ...
= γt
= 0.
´Ł , æŁæ Œ (8.8) º æ ºŁ Ø ŁæŁ Ø, æº º , æŁæ Œ (8.8) º æ Æ Łæ L
1
+ L
2
. ª
dim
(L
1
+L
2
) = Łæº Œ Æ Łæ (8.8) = r
+(s
−r
)+(t
−r
) = s
+
+t
−r
= dim L
1
+dim L
2
−dim L
= dim L
1
++dim L
2
−dim
(L
1
∩L
2
). 
º æ Ł
8.5.1.1.
— æ Ø æ ß æ æ Ø æº ª ßı.
˜ Œ º æ . ˜ Øæ Ł º , æºŁ L
1
+ L
2
æ ,
º Ł L
1
∩L
2
= {0}, dim
{0} = 0. ˇ º , dim
(L
1
⊕L
2
) =
= dim L
1
+ dim L
2
. 
ˆº 9
¸Ł Ø ß ß ºŁ Ø æ æ
9.1 ˇ æ æ Ł ºª Æ ºŁ Ø ßı
ˇ æ V
Ł V
0
ºŁ Ø ßı æ æ Ł Ł æ ß º k
.
˛ º Ł 9.1.1. ¸Ł Ø ß Ł æ æ V
æ æ V
0
Ł Ł º k
ß æ æ Œ Æ Ł f
: V
→ V
0
, º ø æº Ł :
1. (∀ a,b
∈ V
) f
(a
+ b
) = f
(a
) + f
(b
);
2. (∀ α
∈ k,a
∈ V
) f
(αa
) = αf
(a
).
´Ł , Ł ºŁ Ø ßØ ¿ º æ Æ Æø Ł -
Ł Ł Ł ¿. ´ æº Ł Ł , Æ º æ Æß f
Æߺ
ÆŁ Œ Ł Ø. æº Ł 1) , f
º æ ª Ł (V,
+)
 . æº Ł 1) ß æ æº Ł Ł Ł æ Ł, æº Ł 2) ß æ æº Ł æ Ł. . æº Ł 1) ß æ æº Ł Ł Ł æ Ł, æº Ł 2) ß æ æº Ł æ Ł.
˛ º Ł 9.1.2. ¸Ł Ø ß Ł æ æ V
æ æ V
0
Ł Ł æ ß º k
ß æ æ Œ
58
9.1. ˇ æ æ Ł ºª Æ ºŁ Ø ßı
Æ Ł f
: V
→ V
0
, º ø æº Ł ºŁ Ø æ Ł:
(∀ α,β
∈ k, a,b
∈ V
) f
(αa
+ βb
) = αf
(a
) + βf
(b
).
˛Æ Ł L
(V,V
0
)
æ æ ı ºŁ Ø ßı Ł æ æ V
æ æ V
0
. ˝ æ ææ Ł
ºª Æ Ł æŒŁ ŁŁ: æº Ł Ł ł Ł .
˛ º Ł 9.1.3. ˇ æ f,g
∈ L
(V,V
0
) Ł α
∈ k
. ˇ º ª , (f
+
g
)(a
) = f
(a
) + g
(a
) Ł (αf
)(a
) = αf
(a
).
˛ º Ł 9.1.3 Œ Œ æ ßæº , f
+ g
Ł αf
º æ ºŁ Ø ß Ł Ł.
˜ Øæ Ł º , (∀ α,β
∈ k, a,b
∈ V
) (f
+g
)(αa
+βb
) = f
(αa
+βb
)+
+g
(αa
+βb
) = αf
(a
)+βf
(b
)+αg
(a
)+βg
(b
) = α
(f
(a
)+g
(a
))+β
(f
(b
)+
+ g
(b
)) = α
(f
+ g
)(a
) + β
(f
+ g
)(b
).
º º f
+ g
∈ L
(V,V
0
).
¯ø ø Œ ß æ , αf
∈ L
(V,V
0
).
¯˛—¯ 9.1.1. æ L
(V,V
0
), ææ æ æ -
º ß Ł Ø ºª Æ Ł æŒ Ø Ł Ø æº Ł Ł ł Ø ºª Æ Ł æŒ Ø Ł Ø Ł , Æ ºŁ Ø æ æ º k
.
˜ Œ º æ . ˇ æ f,g,h
∈ L
(V,V
0
),α,β,
1 ∈ k
. ˜º Œ º æ ß æ Œ , ß º æ 7 ŒæŁ ºŁ Ø ª æ æ , Ł
1. f
+ g
= g
+ f
;
2. f
+ (g
+ h
) = (f
+ g
) + h
;
3. (∀ f,g
)(∃ h
) g
+ h
= f
;
4. α
(f
+ g
) = αf
+ αg
;
5. (α
+ β
)f
= αf
+ βf
;
6. (αβ
)f
= α
(βf
) = β
(αf
);
7. 1 · f
= f
.
ˇ Ł Œ ß Ł Łı.
1) ¨ (∀ a
∈ V
) (f
+g
)(a
) = f
(a
)+g
(a
) = g
(a
)+f
(a
) = (g
+f
)(a
).
º º , f
+ g
= g
+ f
.
3) ¨ f,g
∈ L
(V,V
0
). — ææ Ł Æ Ł h
: V
→ V
0
, -
º æº øŁ Æ (∀ a
∈ V
) h
(a
) = f
(a
) − g
(a
). ¸ ªŒ -
| Œ
|
,
|
Æ
|
Ł
|
º æº
|
Ł ºŁ Ø æ Ł, æº -
|
| º
|
, h
∈ L
(V,V
0
). ˇ
|
æ Ł
|
(∀ a
∈ V
)
|
(g
+h
)(a
) = g
(a
)+h
(a
) =
|
= g
(a
) + (f
(a
) − g
(a
)) = f
(a
). º º , g
+ h
= f
. 
| ˇ æ V,V
0
,V
00
Ł ºŁ Ø ßı
|
æ æ
|
º k
,
|
æ
|
| f
∈ L
(V,V
0
), ϕ
∈ L
(V
0
,V
00
). ª
|
ææ
|
Ł
|
Œ
|
Ł Ł
|
| ºŁ Ø ßı ϕ
◦f
: V
→ V
00
, Œ
|
º
|
æ æº
|
øŁ
|
| Æ (ϕ
◦ f
)(a
) = ϕ
(f
(a
)). Œ
|
Ł Ł
|
ϕ
◦ f
Æ
|
Æ
|
ϕf
.
ˇ Œ , ϕf
æ ºŁ Ø ßØ Ł æ æ V
V
00
.
˜ Øæ Ł º , ϕf
(αa
+ βb
) = ϕ
(f
(αa
+ βb
)) = ϕ
(αf
(a
) + βf
(b
)) = = αϕ
(f
(a
)) + βϕ
(f
(b
)) = α
(ϕf
)(a
) + β
(ϕf
)(b
). º º , ϕf
∈
∈ L
(V,V
00
).
¯˛—¯ 9.1.2. ˇ æ f,g
∈ L
(V,V
0
), ϕ,ψ
∈ L
(V
0
,V
00
), h
∈ L
(V
00
,V
000
), α
∈ k
. ª æ ºŁ ß æº øŁ æ ł Ł :
1. ϕ
(f
+ g
) = ϕf
+ ϕg
;
2. (ϕ
+ ψ
)f
= ϕf
+ ψf
;
3. h
(ϕf
) = (hϕ
)f
;
4. α
(ϕf
) = (αϕ
)f
= ϕ
(αf
).
9.1. ˇ æ æ Ł ºª Æ ºŁ Ø ßı
| ˇ æ f,g,ϕ,ψ,h
∈ L
(V,V
), æ ºŁ Ø ß
Ø ª æ æ V
æ Æ .
|
ß Ł ºŁ-
|
| ˛ º Ł 9.1.4. ¸Ł Ø ßØ Ł V
V
ß æ Ł .
|
-
|
| ˝ æ L
(V,V
) ææ Ł ºª Æ
|
Ł æŒ
|
| Ł Ł . ¯æºŁ f,ϕ
∈ L
(V,V
),
|
º ª
|
| ϕf
= ϕ
◦ f
: V
→ V
, ϕf
∈ L
(V,V
). ˜º
|
Ø
|
ŁŁ
|
Ł
|
| æ ºŁ ß æ ł Ł 1) 4)
|
ß 9.1.2.
|
| ¯˛—¯ 9.1.3. æ L
(V,V
), ææ
|
æ
|
æ -
|
| º ß Ł ºª Æ Ł æŒŁ Ł
|
Ł Ł:
|
Ł Ł
|
| æº Ł Ł Ł Ł ł Ł º k
.
|
Ł
|
, Æ
|
ºª Æ
|
| 9.1.3 , ŁŁ æº øŁ 10 ŒæŁ :
1) 7) ŒæŁ ß ºŁ Ø ª æ æ ;
8) f
(g
+ h
) = fg
+ fh
, (f
+ g
)h
= fh
+ gh
;
9) f
(gh
) = (fg
)h
;
10) α
(fg
) = (αf
)g
= f
(αg
).
|
æ
|
L
(V,V
)
|
º -
|
| ˚ Œ Ł æ Œ ºª Æ , ºª Æ ºŁ Ø ßı
|
æ æ
|
Ł Ł
|
ı ºª Æ Ł æŒŁı æ Œ : æ Œ ß ºŁ Ø ª æ æ ( ŒæŁ ß 1) 7)) Ł æ Œ ß Œ º ( ŒæŁ ß 1) 3) Ł 8) 9)). Ł æ Œ ß æ ß æ Æ Ø æ Øæ 10).
´ º ł Øł , æ L
(V,V
) Æ Æ L
(V
). ˇ Ł ß
:
1) ˝ º Ø ºŁ Ø ßØ Ł L
(V
)
. ˛ Æ æ 0V
.
˛ º æ ŒŁ Æ (∀ a
∈ V
) 0V
(a
) = 0. æ ,
(∀ f
∈ L
(V
)) f
+ 0V
= f
.
| 2) æ ßØ ºŁ Ø ßØ Ł L
(V
)
. ˛Æ
|
æ 1V
.
|
| ˛ º æ ŒŁ Æ (∀ a
∈ V
) 1V
(a
)
|
=
|
a
. æ ,
|
| (∀ f
∈ L
(V
)) 1V
· f
= f
· 1V
= f
.
|
,
|
ºª Æ L
(V
)
|
| æ Ł Ł .
|
| 9.2 Ł ºŁ
|
Ø ª
|
Œ
|
| ºŁ Ø
|
æ æ
|
| ˙ æ ß º Ł Æ
ª dim V
= n
.
|
Ł æ ı ºŁ Ø ßı
|
ºª Æ ß L
(V
)
,
|
| ¯˛—¯ 9.2.1. ˇ æ
|
e
1
,e
2
,...,en
Æ
|
Łæ ºŁ
|
Ø
|
ª æ -
|
| æ V
. ˇ æ V
0
|
ª ºŁ Ø æ
|
æ
|
º k
Ł
|
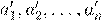 Ł º æŁæ Œ Ł V
0
. ª æ ø æ - Ł º æŁæ Œ Ł V
0
. ª æ ø æ -
| Ł æ
|
ßØ ºŁ
|
Ø ßØ
|
f
∈ L
(V,V
0
),
|
øŁØ Æ Łæ
|
| æ æ
|
V
|
æŁæ
|
Œ æ
|
æ
|
V
0,
|
æ
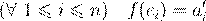 . .
˜ Œ º æ . 1) ¯ Ł æ æ .
ˇ æ æ ø æ ºŁ Ø ßØ f
∈ L
(V,V
0
)
Œ Ø, (∀ 1
6
6 i
6 n
) f
(ei
) = a
0
i
. ¸ Æ Ø Œ a
∈ V
æ Ł Ł 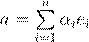 . ª . ª
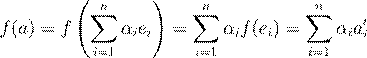 . .
˜ æ Ł , æ ø æ ª Ø ºŁ Ø ßØ f
1
∈ L
(V,V
0
)
, -
º øŁØ æº Ł 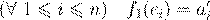 . ª . ª
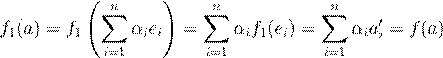 . .
º º f
1
= f
.
2) ø æ Ł .
ˇ æ a
∈ V
. ª 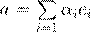 n
. ˛ ºŁ Æ Ł f
: V
→ V
0
æº øŁ Æ n
. ˛ ºŁ Æ Ł f
: V
→ V
0
æº øŁ Æ
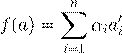 . .
ˇ Œ , Æ Ł º æº Ł ºŁ Ø æ Ł. ˜ Øæ Ł º , æ 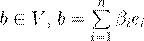 . ª . ª
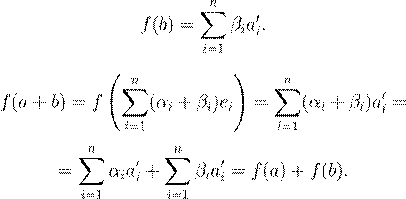
¯ø ø Œ ß æ , f
(αa
) = αf
(a
), ª α
∈ k
. ŒŁ Æ ,
Æ Ł f
∈ L
(V,V
0
). ˝ Œ , (∀ 1 6 i
6 1) f
(ei
) = f
(0·e
1
+...
+
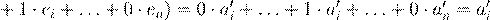 . . 
º æ Ł
9.2.1.1.
¸Ł Ø ßØ Ł V
V
0
º æ Æ Ł Æ Łæ ßı Œ æ æ V
. ß Œ Ł Œ º æ Ø æ Ł ß 9.2.1.
| º æ Ł 9.2.1.2.
|
æ
|
ºŁ
|
Ø ßı
|
Ł V V
0
|
ı Ł -
|
| æ Ł
|
æ
|
æ ŁŁ æ
|
æ
|
ßı
|
| æŁæ Ł n
-
|
Œ
|
æ
|
æ
|
V
.
|
| ˇ æ V
|
ºŁ Ø
|
æ
|
æ
|
º k
, dim V
|
= n
,
|
| e
1
,e
2
,...,en
|
Æ Łæ
|
æ
|
æ
|
V
. ˇ æ ,
|
º , f
∈ L
(V
),
|
æº -
|
| æ Ł Ł
|
ß 9.2.1,
|
Ł æ
|
ß Æ
|
º -
|
| æ Æ
|
Ł Æ Łæ ßı
|
Œ
|
f
(e
1
),f
(e
2
),...,f
(en
) ∈ V
. —
|
º Ł
|
Ł Æ ß Æ Łæ æ æ V
, º Ł
f
(e
1) = α
11e
1 + α
12e
2 + ...
+ α
1n
e
n
;
f
(e
2
) = α
21
e
1
+ α
22
e
2
+ ...
+ α
2n
en
; (9.1)
...
f
(e
n
) = α
n
1e
1 + α
n
2e
2 + ...
+ α
nn
e
n
.
| ˛ º Ł 9.2.1. Ł Ø ºŁ
|
Ø
|
ª
|
f
∈ L
(V
) -
|
| æŁ º Æ Łæ e
1
,e
2
,...,en
ß
|
æ
|
Ł
|
,
|
æ Ł Œ
|
| Ł , æ æ º Ø Ł Œ Ł Ł Æ Łæ ßı Œ Æ Łæ.
|
ºŁ Ø
|
ª
|
ß Ł Æ
|
| >
α
11 α
12 ... α
1n
α
21 α
22 ... α
2n
A
f
|e
e = ... ... ... ...
α
n
1 α
n
2 ... α
nn
|
=
|
α
11
α
12
...
α
1n
|
α
21 α
22 ... α
2n
|
... αn
1
... αn
2
. ... ...
... αnn
|
| ˛ º Ł 9.2.2. Ł Ø ºŁ Ø
|
ª
|
f
∈ L
(V
) æŁ-
|
| º Æ Łæ e
1
,e
2
,...,en
ß æ
|
Ł , æ
|
ºÆ
|
Ł Œ Ø º -
|
| æ Œ Ł ß æ ºÆ ß Œ f
(e
1
),f
(e
2
),...,f
(en
) æŁ º -
|
 Łæ e
, æ Łæ e
, æ
e
Af
|
e
e = (f
ˇ
(e
1
)|e
e,f
ˇ
(e
2
)|e
e,...,f
ˇ
(en
)|e
e).
˛ º Ł 9.2.3. ¯æºŁ Æ Ł
e
1
f
(e
1
)
e
2
f
(e
2
)
e
= Ł f
(e
) = ,
e ...
e ...
en
f
(en
)
 Ø ºŁ Ø ª f
æŁ º Æ Łæ e
ß æ Ø ºŁ Ø ª f
æŁ º Æ Łæ e
ß æ
e
Ł Af
, º Ł æ
f
(e
e) = A
>
f
e.
e
¯˛—¯ 9.2.2. ˇ Ł ŁŒæŁ Æ Łæ e
e
ºŁ Ø ª æ æ V
, dim V
= n
, Æ Ł σ
: L
(V
) → M
(n,k
), æ æ º ø
ºŁ Ø f
ª Ł æŁ º Æ Łæ 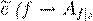 ), ),
º æ Ł Ł ºª Æ ß ºŁ Ø ßı L
(V
) ºª Æ Œ ßı Ł n
-ª Œ M
(n,k
).
˜ Œ º æ . ˇ e
e
Œ ßØ Æ Łæ æ æ V
. — ææ Ł
Æ Ł σ
: L
(V
) → M
(n,k
), σ
(f
) = Af
, ª Af
Ł ºŁ Ø-
ª f
æŁ º Æ Łæ e
e
. ˇ Œ , Æ Ł º æ Ł Ł .
1) ¨ œ Œ Ł æ σ
.
ˇ æ σ
(f
) = σ
(g
), ª f,g
∈ L
(V
). , Af
= Ag
⇒
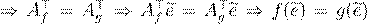 . ß º ŁºŁ, Æ ß . ß º ŁºŁ, Æ ß
Æ Łæ ßı º æ æ V
æ . ª æº æ Ł Ł ß 9.2.1 æº , f
= g
.
2) œ Œ Ł æ σ
.
ˇ æ A
∈ M
(n,k
). ˇ æ Ł n
Œ æ æ V
Œ, Æß Œ Ł ß æ ºÆ ß Łı Œ æŁ º Æ Łæ e
e
æ ºŁ æ æ ºÆ Ł Ł ß A
. ª 9.2.1 æ ø æ ºŁ Ø ßØ f
∈ L
(V
), øŁØ Æ Łæ e
e
æ ß Ł Œ ß.
ˇ æ Ł Æ Ł 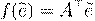 . ˛ æ Ł , æºŁ æ Ł . ˛ æ Ł , æºŁ æ Ł
æ º Ł 9.2.3, A
>
= A
>
f
. ŒŁ Æ , σ
(f
) = Af
= A
.
3) ı Ł ŁØ.
ˇ æ f,g
∈ L
(V
) Ł Af
,Ag
Ł ß Łı ºŁ Ø ßı æŁ º Æ Łæ e
e
. ª 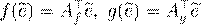 . .
— ææ Ł Øæ Ł æ ß ºŁ Ø ßı f
+ g
Æ Łæ ß
Œ ß. Ø æ ß, 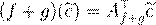 . .
ª Ø æ ß, 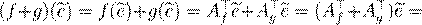
= (Af
+ Ag
)>
e
.
˛ æ , 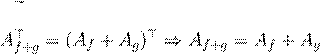 . ŒŁ Æ , - . ŒŁ Æ , -
Ł æ ß ºŁ Ø ßı æ Ł Łı . º º
σ
(f
+ g
) = Af
+g
= Af
+ Ag
= σ
(f
) + σ
(g
),
æ Æ Ł σ
æ ı æº Ł .
— ææ Ł Øæ Ł Ł Ł ºŁ Ø ßı fg
Æ Łæ ß Œ ß. Ø æ ß, 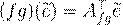 . .
ª Ø æ ß, 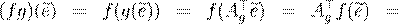
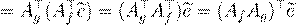 . .
˛ æ , A
>fg
= (A
f
A
g
)> ⇒ A
fg
= A
f
A
g
, æ Ł Ł -
Ł ºŁ Ø ßı Ł Ł Ł Łı . º º
σ
(fg
) = Afg
= Af
Ag
= σ
(f
)σ
(g
),
| æ
|
Æ
|
Ł σ
æ ı
|
Ł .
|
| ˝ Œ
|
, æ
|
æ æ
|
Œ
|
ß
|
æ ,
|
Aαf
= αAf
⇒ σ
(αf
) =
|
= ασ
(f
), ª α
∈ k
. 
| ˇ º Ł
|
9.2.1. ˚
|
Ł ßØ æ ºÆ Æ
|
Œ
|
Ł Ø-
|
| æ ŁŁ ºŁ Ø ß
|
Œ Ł æ
|
ºÆ
|
ª Œ-
|
| ,
æ
|
æº
|
Ł ª ºŁ Ø
f
(ˇ
a
) = Af
a.
ˇ
|
ª
|
,
|
| ˜ Œ º æ
|
. ˜ Øæ Ł
|
º , Œ a
= a
ˇ>
e
e
.
|
Ø æ ß,
|
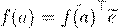 . ª Ø æ ß, . ª Ø æ ß,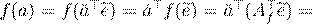
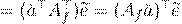 . ¨ , f
(ˇ
a
)>
= (Af
a
ˇ)>
⇒ f
(ˇ
a
) = Af
a
ˇ. . ¨ , f
(ˇ
a
)>
= (Af
a
ˇ)>
⇒ f
(ˇ
a
) = Af
a
ˇ. 
˛ º Ł 9.2.4. Ł B
ß æ Æ Ø Ł A
(B
∼
A
) º k
, æºŁ æ ø æ æ Æ Ł Q
æ º Ł Ł º k
Π,
B
= Q
−1
AQ.
| ¨ ª ª , Ł B
º
|
æ Ł
|
Ł -
|
| Ł ß A
æ ø Ł ß Q
, ŁºŁ Ł Ł ß A
æ ø Ł ß Q
.
|
B
Æ
|
Ł -
|
| ˙ Ł 9.2.1. ¯æºŁ Ł ß B
Ł A
Œ ß Ł Ł Œ Ø æ Ł.
|
Æ ß, Ł
|
º ß Æß
|
| ˇ º Ł 9.2.2. ˛ ł Ł ÆŁ Ł º æ Ł æ M
(n,k
).
˜ Œ º æ . 1) — º ŒæŁ æ .
|
º æ
|
ł Ł Œ-
|
| ¨ A
= E
−1
AE
, ª A
∼ A
, º Ł .
2) Ł Ł æ .
|
Ł ß Q
Łª
|
Ł Ł
|
| ˇ æ B
∼ A
. , (∃ Q,
|Q
| 6= 0) B
= Q
−1
AQ
⇒
⇒ QBQ
−1 = Q
(Q
−1AQ
)Q
−1 ⇒ QBQ
−1 = A
⇒ A
= (Q
−1)−1BQ
−1 ⇒
⇒ A
∼ B
, º Ł ß Q
Łª Q
−1
.
3) Ł Ł æ .
|
ˇ æ C
∼ B, B
∼ A
, ª (∃ R,
|R
| 6= 0) C
= R
−1
BR
, Ł
(∃ Q,
|Q
| 6= 0) B
= Q
−1
AQ
. º º C
= R
−1
(Q
−1
AQ
)R
= = (QR
)−1
A
(QR
) ⇒ C
∼ A
, º Ł ß Q
Łª QR
. 
| ¯˛—¯ 9.2.3.
|
Ł ß ª Ł ª ºŁ
|
Ø ª
|
f
|
| ºŁ ßı Æ
|
Łæ ı
|
Æ ß. ˇ Ł Ł
|
A
f
|u
º
e
|
æ
|
Ł
|
| Ł ß A
f
|e
e
|
æ
|
Ł Ł Ł øŁ
|
Ł ß
|
ı
|
| Æ Łæ e
Œ Æ Łæ
e
|
u
, e
|
æ
A
f
|u
= Q
−1A
f
|e
Q,
e e
|
| ª Q
Ł
|
ı e
Πu
.
|
e e
˜ Œ º æ . ˇ æ dim V
= n, e
e
Ł u
e
Æ Łæ æ æ
V
, f
∈ L
(V
), Af
|
e
e
Ł Af
|
u
e
Ł ß f
æŁ º e
e Ł u
e æ æ . ª
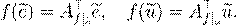
ˇ æ , Œ , Q
Ł ı  Œ , æ Œ , æ 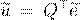 . .
Ø æ ß, 
= (Af
|
e
Q
)>
e
e. ª Ø æ ß, 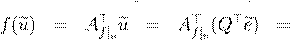
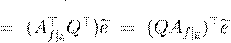 . ŒŁ Æ , . ŒŁ Æ , 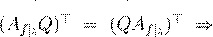
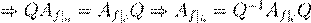 . . 
| º æ
|
Ł 9.2.3.1. ¯æºŁ Af
|
Ł ºŁ Ø ª
|
f
æŁ-
|
| º
|
Æ Łæ e
e
Ł B
∼ Af
,
|
Ł B
ææ
|
Ł Œ Œ
|
| Ł
æ .
|
ºŁ Ø ª f
|
æŁ º Œ ª
|
ª ª Æ Ł-
|
| ˜ Œ
|
º æ . ˜ Øæ Ł º ,
|
ΠΠΠB
∼ Af
,
|
(∃ Q,
|Q
| 6=
|
| 6= 0)
|
B
= Q
−1
Af
Q
. — ææ Ł
|
ßØ Æ Łæ u
e
= Q
>
e
e
.
|
ΠΠΠQ
|
| æ Æ
|
Ł , u
e
Æ ß Æ Łæ . ˇ
|
9.2.3 Ł
|
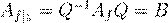 . . 
| 9.3 — ª Ł
|
Œ ºŁ Ø ª
|
| ˇ æ V
Ł V
0
∈ L
(V,V
0
).
|
ºŁ Ø ßı æ
|
æ
|
º
|
k
,
|
æ
|
f
∈
|
˛ º Ł 9.3.1. ˛Æ ºŁ Ø ª f
(Im f
) ß æ æ Æ æ ı º æ æ V
. ºŁ Ø ª f
(Ker f
) ß æ æ ı Œ æ æ V
, Œ ß Ł Æ ŁŁ f
æ º æ æ V
0
.
¨ ª º Ł Ł ,
Im f
= {f
(a
)| a
∈ V
}, Ker f
= {a
∈ V
| f
(a
) = 0}.
9.3. — ª Ł Œ ºŁ Ø ª
ˇ º Ł 9.3.1. Ł Æ ºŁ Ø ª f
∈ L
(V,V
0
)
º æ ºŁ Ø ß Ł æ æ Ł æ æ V
Ł V
0
æ æ .
˜ Œ º æ . ˜ Øæ Ł º , (∀ α,β
∈ k,a,b
∈ Ker f
) Ł
f
(αa
+ βb
) = αf
(a
) + βf
(b
) = α
· 0 + β
· 0 = 0 ⇒ αa
+ βb
∈ Ker f.
, Ker f
º æ æ Ø Ł ß æ æ æ V
, æº º , º æ ª ºŁ Ø ß æ æ .
ˇ æ a
0
,b
0
∈ Imf
. , (∃ a,b
∈ V
) f
(a
) = a
0
,f
(b
) = b
0
.
ª (∀ α,β
∈ k,a
0
,b
0
∈ Im f
) Ł
αa
0
+ βb
0
= αf
(a
) + βf
(b
) = f
(αa
+ βb
) ∈ Im f.
˛ æ Im f
º æ æ Ø Ł ß æ æ æ V
0
, æº º , º æ ª ºŁ Ø ß æ æ . 
| ˇ º Ł 9.3.2. ¯æºŁ V
|
Œ
|
ºŁ
|
Ø
|
æ
|
æ
|
| Ł f
∈ L
(V,V
0
), Ł Æ
|
ºŁ
|
Ø
|
ª
|
f
|
º
|
æ
|
Π-
|
ß Ł ºŁ Ø ß Ł æ æ Ł.
˜ Œ º æ . ´ æ º , Œ Œ Œ V
Œ ºŁ Ø æ æ , Ł º Æ ª æ æ , æ æ Ł Ker f
, Œ º æ Œ ß .
ˇ Ø Œ Æ Im f
. ˇ æ e
1
,e
2
,...,en
Æ Łæ æ æ V
.
ª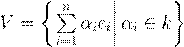 . ª . ª
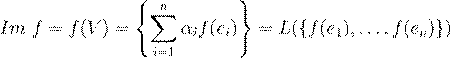 . .
˝ ºŁ Ø Æ º Œ , Œ ß Łæº Œ , º æ Œ Ø Ł Ł
dim L
({f
(e
1
),...,f
(en
)}) = rang
{f
(e
1
),...,f
(en
)}.
º º , Im f
º æ Œ ß ºŁ Ø ß æ -
æ . 
˛ º Ł 9.3.2. ¯æºŁ V
Œ ºŁ Ø æ æ
Ł f
∈ L
(V,V
0
), ª ºŁ Ø ª f r
(f
) ß æ æ ª Æ , Œ ºŁ Ø ª f d
(f
)
ß æ æ ª .
¨ ª º Ł Ł , r
(f
) = dim Im f
, d
(f
) =
= dim Ker f
.
º æ Ł . r
(f
) = r
{f
(e
1
),...,f
(en
)}.
º æ Ł . ¯æºŁ f
∈ L
(V
)
, ª ºŁ Ø ª f
ª Ł ß ª ºŁ Ø ª æŁ º º Æ ª Æ Łæ , æ
r
(f
) = r
(Af
).
˜ Œ º æ . ˜ Øæ Ł º , ß ø æº æ Ł Ł
r
(f
) = r
{f
(e
1
),...,f
(en
)}. — ææ Ł æ ßØ Ł Ł σ
:
V
→ k
n
æŁ º Æ Łæ . ª . ª 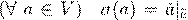 . ˇ Ł Ł Ł ª æŁæ ß Œ Ł æ , . ˇ Ł Ł Ł ª æŁæ ß Œ Ł æ ,
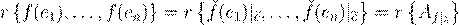 . .

| ¯˛—¯
|
9.3.1 ( ª Ł Œ ºŁ Ø ª ). ¯æºŁ
|
| V
Œ
|
ºŁ Ø æ æ , dim V
= n
, f
∈ L
(V,V
0
),
|
| æ
|
ª Ł Œ ºŁ Ø ª f
æ Ł
|
| æ æ
|
V
, æ r
(f
) + d
(f
) = n
.
|
| ˜ Œ º æ
|
. ´ Æ Ł d
= d
(f
) = dim Ker f
. ˇ æ
|
| e
1
,e
2
,...,ed
|
Æ Łæ Ker f
. ˜ º Ł Æ Łæ Æ Łæ æ -
|
| æ V
, º
|
Ł e
1
,e
2
,...,ed
,ed
+1
,...,en
Æ Łæ V
. ˇ æº æ Ł Œ
|
| º Ł
|
9.3.2 Ł
|
r
(f
) = r
{f
(e
1
),f
(e
2
),...,f
(ed
),f
(ed
+1
),...,f
(en
)} = r
{f
(ed
+1
),...,f
(en
)}.
9.4. ˛Æ Ł æ ºŁ Ø ª
ˇ Œ , Œ ß f
(ed
+1
),...,f
(en
) º æ ºŁ Ø ŁæŁ ß-
Ł. ˇ æ
αd
+1
f
(ed
+1
) + ...
+ αn
f
(en
) = 0;
f
(α
d
+1e
d
+1 + ...
+ α
n
e
n
) = 0 ⇒ α
d
+1e
d
+1 + ...
+ α
n
e
n
∈ Ker f.
— º Ł º Æ Łæ Ker f
. ¨
α
d
+1e
d
+1 + ...
+ α
n
e
n
= β
1e
1 + ...
+ β
d
e
d
;
−β
1e
1 − ...
− β
d
e
d
+ α
d
+1e
d
+1 + ...
+ α
n
e
n
= 0.
ΠΠΠe
1
,e
2
,...,en
Æ Łæ æ æ V
, β
1
= ...
= βd
= αd
+1
=
= ...
= αn
= 0. ŒŁ Æ , Œ ß f
(ed
+1
),...,f
(en
) º æ ºŁ Ø ŁæŁ ß Ł. ª r
(f
) = r
{f
(ed
+1
),...,f
(en
)} = n
− d
⇒ ⇒ r
(f
) + d
(f
) = n
− d
+ d
= n
. 
9.4 ˛Æ Ł æ ºŁ Ø ª
| ˇ æ V
ºŁ Ø æ æ º k
. — ææ Ł ºª Æ
|
| L
(V
)
. ´ Ø ºª Æ æ Ł Ł , º Ł Ł ß ß º æ ßØ 1V
. ˝ Ł , (∀ a
∈ V
) 1V
(a
) = a
.
|
-
|
| ˛ º Ł 9.4.1. ¸Ł Ø ßØ f
∈ L
(V
)
ß æ
|
Æ -
|
| Ł ß , æºŁ Æ Ł Œ Œ º º Ł ºŁŒ Ł Ø º ª
Œ º L
(V
), æ (∃ f
−1
∈ L
(V
)) ff
−1
= f
−1
f
= 1V
.
|
ß
|
| ¯˛—¯ 9.4.1 (Œ Ł ŁØ Æ Ł æ Ł ºŁ Ø ª
|
).
|
| ˜º ª , Æß ºŁ Ø ßØ f
∈ L
(V
) Æߺ Æ Ł ß
|
Æ-
|
| ı Ł Ł æ , Æß Œ Œ Æ Ł Æߺ ÆŁ Œ Ł
|
ß .
|
| ˜ ªŁ Ł æº Ł, f
Æ Ł ª Ł º Œ ª , Œ ª f
Ł Ł V V
.
˜ Œ º æ . 1) ˝ Æı Ł æ .
|
Ł -
|
ˇ æ f
∈ L
(V
)
º æ Æ Ł ß . ˇ º Ł 9.4.1 (∃ f
−1
∈
L
(V
)) ff
−1
= f
−1
f
= 1V
. ˝ Œ , f
º æ ÆŁ Œ Ł Ø.
ˇ æ f
(a
) = f
(b
). ˇ Ł Ł Œ æ Æ Ł f
−1, º -
Ł f
−1
(f
(a
)) = f
−1
(f
(b
)) ⇒ (f
−1
f
)(a
) = (f
−1
f
)(b
) ⇒ 1V
(a
) = 1V
(b
) ⇒
⇒ a
= b
. ˇ æ b
∈ V
. ˝ Œ , (∃ a
∈ V
) f
(a
) = b
. ˇ æ -
Ł Œ b
Πa
= f
−1
(b
). ª f
(a
) = f
(f
−1
(b
)) =
= (ff
−1
)(b
) = 1V
(b
) = b
, æ f
º æ ÆŁ Œ Ł Ø.
2) ˜ æ æ .
ˇ æ ∈ L
(V
) Ł f
º æ ÆŁ Œ Ł Ø. ª (∃ f
−1
: V
→ V
) ff
−1
=
= ff
−1 = 1V
. Æ Ł f
−1 Œ º æ ÆŁ Œ Ł Ø. ˝
Π, f
−1 ∈ L
(V
), æ f
−1 º æº Ł ºŁ Ø-
æ Ł. ˇ æ a,b
∈ V
, ª (∃ a
0
,b
0
∈ V
) f
(a
0
) = a,f
(b
0
) = b
. ˛ æ f
−1
(a
) = a
0
, f
−1
(b
) = b
0
. ´ Ł º ß α,β
∈ k
, æ æ Ł
f
(αa
0
+ βb
0
) = αf
(a
0
) + βf
(b
0
) = αa
+ βb
⇒
⇒ f
−1
(αa
+ βb
) = αa
0
+ βb
0
= αf
−1
(a
) + βf
−1
(b
).
˛ Æ Ł f
−1
º æº Ł ºŁ Ø æ Ł, æº º
f
−1
∈ L
(V
). 
| 9.5 Œ Łæ Ł æŒŁØ
|
ª º
|
Ł ß Ł ºŁ-
|
| Ø
|
ª
|
| ˇ æ k
æ
|
º Ł k
[λ
] Œ º
|
ª
|
º
|
Ł
|
æ ª λ
.
|
| ˛ º Ł
|
9.5.1. λ
- Ł Ø (
|
ª º
|
Ø
|
Ł
|
Ø)
|
º
|
| k
ß æ
|
Ł , º Ł Œ
|
Ø
|
º æ
|
º
|
ß Œ º
|
| k
[λ
], æ
|
ª º ß λ
æ Œ
|
Ł Ł
|
Ł Ł
|
º
|
k
.
|
| λ
- Ł ß
|
挺 ß ,
|
,
|
æŒ º ß
|
| Łº , Ł æŒ º
|
ß
|
Ł ß. ˇ æ
|
A
=
|
 = (αij
), αij
∈ k, i,j
= 1,n
. ŒŁ Ł ß Æ ß æŒ º ß Ł. = (αij
), αij
∈ k, i,j
= 1,n
. ŒŁ Ł ß Æ ß æŒ º ß Ł.
9.5. Œ Łæ Ł æŒŁØ ª º Ł ß Ł ºŁ Ø ª
˛ º Ł 9.5.2. Œ Łæ Ł æŒ Ø Ł Ø º Œ Ø æŒ º Ø Ł ß A
ß æ λ
- Ł Ł λE
− A
, æ
| λ
− α
11 −α
12 ...
−α
1n
α
21 λ
− α
22 ... α
2n
λE
− A
= .
... ... ... ...
−α
n
1 −α
n
2 ... λ
− α
nn
|
| ˛ º Ł 9.5.3. Œ Łæ Ł æŒŁ ª º º
|
æŒ º
|
Ø
|
| Ł ß A
ß æ ºŁ º , ßØ ı Œ
Ł Ø º Ł ß A
.
|
Łæ Ł
|
æŒ Ø
|
| Œ Łæ Ł æŒŁØ ª º Ł ß A
Æ
χA
(λ
) = |λE
− A
|.
|
æ
|
˛ º Ł 9.5.4. º Œ Ø æŒ º Ø Ł ß A
(Tr
(A
)
) ß æ æ º ªº Ø Ł ª ºŁ. ˝ Ø Ł ß A
(N
(A
)
) ß æ ºŁ º .
º Ł ,
Tr
(A
) = α
11
+ α
22
+ ...
+ αnn
, N
(A
) = |A
|.
æ , Tr
(αA
+ βB
) = αTr
(A
) + βTr
(B
); N
(AB
) = N
(A
) · N
(B
).
¯˛—¯ 9.5.1 ( æ ŁŁ ı Œ Łæ Ł æŒ ª ª º -
). Œ Łæ Ł æŒŁØ ª º º æŒ º Ø Ł ß A
º æ Ł ß ª º λ
æ Ł n
, Ł øŁ æº -
øŁØ Ł : χA
(λ
) = λn
− Tr
(A
)λn
−1
+ ...
+ (−1)n
N
(A
).
˜ Œ º æ . ¨ ,
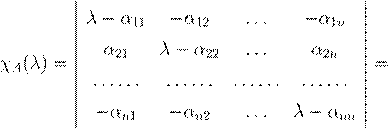
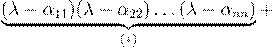 ø (n
!
− 1)
æº ª ßı. ø (n
!
− 1)
æº ª ßı.
´ æ łŁıæ (n
! − 1)
æº ª ßı æ æ Œ Ø Ø
º ªº Ø Ł ª ºŁ. ˇ æ łŁ æ æº ª ß ª æ λ
ßł , n
− 2
. º ª ß æ λn
Ł æ λn
−1
º æ æ Ł Ł (∗)
. ´ Ł Ł (∗) λ
n
ı Ł æ Œ Ł Ł 1.
˚ Ł Ł Ł λn
−1
−α
11
−α
22
−...
−αnn
= −Tr
(A
). ˇ º
χA
(λ
) = λn
− Tr
(A
)λn
−1
+ αn
−2
λn
−2
+ ...
+ α
1
λ
+ α
0
, ª α
0
= χA
(0) = = |0 · E
− A
| = | − A
| = (−1)n
|A
| = (−1)n
N
(A
). 
| ˛ º Ł 9.5.5.
|
Œ Łæ Ł
|
æŒŁ Ł Œ
|
Ł ( Łæº Ł)
|
Ł-
|
| ß A
ß æ æ
|
n
Œ Ø ı
|
Œ Łæ Ł
|
æŒ ª ª º
|
, º -
|
| øŁ , Æø ª
|
, ºª Æ Ł
|
æŒ ßŒ
|
ŁŁ æ ª
|
º k
.
|
| ˙ Ł 9.5.1. ´ æ
|
æ
|
º k
|
Æø Æß
|
ı Œ-
|
Łæ Ł æŒŁı Œ Ø, ŁºŁ Łı Æß ł , n
.
ˇ Ł
: k
=
R,
 ! !
;
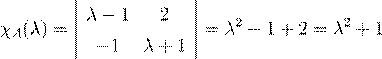 . .
 χA
(λ
) = 0 ⇒ λ
2
+ 1 = 0 ⇒ λ
1
= i, λ
2
= −i
. ´Ł , λ
1
,λ
2
∈/
∈/
R, λ
1
,λ
2
∈ R = C. ´ º Øł ı Œ Łæ Ł æŒŁ Œ Ł Ł ß χA
(λ
) = 0 ⇒ λ
2
+ 1 = 0 ⇒ λ
1
= i, λ
2
= −i
. ´Ł , λ
1
,λ
2
∈/
∈/
R, λ
1
,λ
2
∈ R = C. ´ º Øł ı Œ Łæ Ł æŒŁ Œ Ł Ł ß
A
Æ Æ λ
1
,λ
2
,...,λn
.
º æ Ł
9.5.1.1.
ı Œ Łæ Ł æŒŁı Œ Ø Ł ß A
æº , Ł Ł ı Œ Łæ Ł æŒŁı Œ Ø .
˜ Œ º æ .
ß Œ Ł ß 9.5.1 Ł ß ´Ł . ˜ Øæ Ł º ,
λ
1
+ λ
2
+ ...
+ λ
+
n
= −(−Tr
(A
)) = Tr
(A
),
9.5. Œ Łæ Ł æŒŁØ ª º Ł ß Ł ºŁ Ø ª
λ
1
,λ
2
,...,λn
= (−1)n
· (−1)n
· N
(A
) = N
(A
).

º æ Ł
9.5.1.2.
˚ Ł A
æ Æ ª Ł º Œ ª , Œ ª æ ı Œ Łæ Ł æŒŁ Łæº ºŁ ß º .
˜ Œ º æ . ´ æ º , |A
| 6= 0 ⇔ N
(A
) = 06 ⇔ λ
1
·λ
2
·...
·λn
6= 0 ⇔ (∀ 1 6 i
6 n
) λi
6= 0. 
ˇ æ V
Œ ºŁ Ø æ æ k
Ł f
∈ L
(V
).
ˇ æ e
˜
Æ Łæ V Ł Af
|
e
˜
Ł f
æŁ º Æ Łæ e
˜
. Œ Œ Œ
Ł ŁæŁ Æ Łæ , Ł ı Œ Łæ Ł æŒ Ø Ł ß
º ºŁ Ø ª Ł æ .
ˇ º Ł 9.5.1. Œ Łæ Ł æŒŁ ª º ß Æ ßı Ł ß.
˜ Œ º æ . ˇ æ B
∼ A
, æ (∃ Q,
|Q
| 6= 0) B
= Q
−1
AQ
. — ææ Ł ı Œ Łæ Ł æŒŁØ ª º Ł ß B
. χB
(λ
) =
|λE
−
− B
| = |λE
− Q
−1
AQ
| = |Q
−1
(λE
)Q
− Q
−1
AQ
| = |Q
−1
(λE
− A
)Q
| = = |Q
−1
||λE
− A
||Q
| = |λE
− A
| = χA
(λ
). 
º æ Ł .
º ß Ł ß Æ ßı Ł ß.
º æ Ł .
Œ Łæ Ł æŒŁØ ª º Ł ß ºŁ Ø ª -
ŁæŁ ßÆ Æ Łæ , æŁ º Œ ª æ Łº æ -
Ł , ŁæŁ º Œ æ ª ºŁ Ø ª .
˛ º Ł 9.5.6. Œ Łæ Ł æŒŁ ª º ºŁ Ø ª ß æ ı Œ Łæ Ł æŒŁØ ª º Ł ß ª ºŁ ت æŁ º º Æ ª Æ Łæ .
˛Æ Ł ı Œ Łæ Ł æŒŁØ ª º ºŁ Ø ª f
-
χf
(λ
). ª χf
(λ
) = χA
f
(λ
).
˛ º Ł 9.5.7. º Tr
(f
)
Ł Ø N
(f
)
ºŁ Ø ª
f
ß æ æº Ł Ł ß ª ºŁ Ø ª æŁ-
º º Æ ª Æ Łæ .
˛ º Ł 9.5.8. Œ Łæ Ł æŒŁ Ł Œ Ł ºŁ Ø ª ß æ æ Œ Ł ı Œ Łæ Ł æŒ ª ª º ª ºŁØ ª , º øŁ , Æø æº , ºª Æ Ł æŒ ßŒ ŁŁ æ ª º .
9.6 Ææ ß Œ ß Ł æ Ææ ß Ł ºŁ Ø ª Ł Ł ß
ˇ æ V
ºŁ Ø æ æ º k
, f
∈ L
(V
)
. ˇ æ V
0
ºŁ Ø æ æ æ æ V
. ´ Æø æº f
(V
0
)
⊂ V
,
Æß Œ, f
(V
0
) ⊂ V
0
.
˛ º Ł 9.6.1. ˇ æ æ V
0
ºŁ Ø ª æ æ V
ß æ Ł Ł ß æŁ º ºŁ Ø ª f
∈ L
(V
)
,
æºŁ f
(V
0
)
⊂ V
0
, æ º Æ Ø Œ Ł æ æ V
0
ı Ł
Œ ª æ æ .
˙ Ø æ Ł Ł ßı Ł Ł ßı æ æ . ˇ æ V
0
Ł Ł æ æ . ´ º Æ Ø
Πa
∈ V
0
,a
6= 0. ΠΠΠdim V
0
= 1, Πa
Œ æ Æ Łæ V
0
Ł ª V
0
= {αa
|α
∈ k
}. f
(a
) Æ Ł º
V
0
, ΠΠΠV
0
Ł Ł . ª f
(a
) = αa, a
6= 0,α
∈ k
.
˛Æ , æ V
0
æ æ Ł a
6= 0, a
∈
V
0
, f
(a
) = αa
, ª α
∈ k
. ΠΠΠV
0
æ æ , a
Œ æ Æ Łæ V
0
. ˇ V
0
= {βa
|β
∈ k
}. æ Ł
f
(βa
) = βf
(a
) = β
(αa
) = (βα
)a
∈ V
0
. ŒŁ Æ f
(V
0
) ⊂ V
0
, æ
V
0
Ł Ł æ æ . ŒŁ Æ Ł Ł -
9.6. Ææ ß Œ ß Ł æ Ææ ß Ł ºŁ Ø ª Ł Ł ß
ßı Ł Ł ßı æ æ Ł Ł æ Œ Ł Ł º ßı
| Πa
∈ V
0
, º Œ ßı f
(a
) = αa
, ª α
∈ k
.
˛ º Ł 9.6.2. Œ º α
ß æ æ Ææ ß Ł ºŁ-
Ø ª f
∈ L
(V
)
, æºŁ æ ø æ º Ø Œ a
∈ V
Œ Ø, f
(a
) = αa
. ´ æº Œ a
ß æ æ Ææ ß
|
| Œ
|
ºŁ Ø ª f
, Ł º øŁ æŒ º α
.
|
| ´
|
æº ª , α
Ł a
æ Ł º
|
øŁ ª ª
|
| æ Ææ
|
Ł Ł æ Ææ ßØ Œ ºŁ Ø ª
|
f
.
|
| ˛
|
º Ł 9.6.3. ˆ , æŒ º α
Ł º
|
Ø æ ºÆ X
6= 0
|
| Ł k
n
|
æ Ł º øŁ ª ª æ Ææ
|
Ł Ł æ Ææ -
|
| ßØ
|
Œ Ł ß A
∈ M
(n,k
), æºŁ AX
= αX
.
|
| ˇ
|
º Ł 9.6.1. ˜º ª , Æß æŒ º α
Ł
|
Πa
∈ V
ÆߺŁ
|
| Ł
|
º øŁ Ł ª ª æ Ææ ß Ł
|
Ł æ Ææ ß
|
| Œ
|
ºŁ Ø ª f
Œ ª ºŁ
|
Ø ª æ -
|
| æ
|
V
Æı Ł Ł æ , Æß α
Ł Œ
|
Ł ßØ æ ºÆ
|
| a
ˇ
|
æŁ º Œ ª Æ Łæ ÆߺŁ Ł º
|
øŁ Ł ª ª
|
| æ Ææ
|
ß Ł Ł æ Ææ ß Œ
|
Ł ß Af
ª
|
| ºŁ Ø ª æŁ º ª Æ Łæ .
|
˜ Œ º æ . ˜ Øæ Ł º , æ f
(a
) = αa
, ª a
6= 0 Ł α
∈ k
,
ª f
(a
) = αa
⇔ f
(ˇ
a
) = αa
ˇ ⇔ Af
a
ˇ = αa
ˇ. ˇ Ł a
ˇ 6= 0 ⇔ a
6= 0. 
| ¯˛—¯ 9.6.1 (Œ Ł
|
ŁØ æ Ææ
|
ª Ł ). ˜º
|
ª ,
|
| Æß æŒ º α
Æߺ æ Ææ
|
ß
|
Ł Ł ß A
(ºŁ
|
Ø ª
|
| Œ ª
|
æ æ
|
) Æı Ł Ł æ
|
,
|
| Æß α
Æߺ ı Œ Łæ Ł
|
æŒŁ Œ
|
Ł ß A
(ºŁ Ø
|
ª -
|
| ), º øŁ æ
|
º .
|
| ˜ Œ º æ . 1) ˝ Æı
|
Ł æ .
|
| ˇ æ α
º æ æ Ææ
|
ß Ł
|
Ł ß A
,
|
,
|
| AX
= αX,
|
(9.2)
|
| ª
|
X
6= 0 Ł X
∈ kn
. ˇ
|
Łł æ (9.2):
αEX
− AX
= 0,
|
| (αE
− A
)X
= 0.
|
(9.3)
|
| ˝
|
æ (9.3)
|
æ Œ Œ
|
æŁæ
|
n
-
|
| ºŁ
|
Ø ßı ŁØ æ n
|
Ł æ ß Ł. æŁæ
|
Łæ
|
-
|
| Ł
|
Ł . ´Ł ,
|
º ß ł Ł
|
Ø æŁæ ß
|
º æ
|
| æ
|
ºÆ X
∈ kn
, X
6= 0.
|
ª æº æ Ł Ł Œ Ł Ł ºŁ Ł
|
-
|
º ª ł Ł ˛ ¸ æº , ºŁ º æŁæ ß (9.3) º
Æß º , æ |αE
− A
| = 0. ŒŁ Æ χA
(α
) = 0, æº º α
º æ ı Œ Łæ Ł æŒŁ Œ Ł ß A
Ł α
∈ k
.
2) ˜ æ æ .
ˇ æ α
∈ k
Ł α
º æ ı Œ Łæ Ł æŒŁ Œ Ł ß A
.
ª χA
(α
) = 0, , |αE
−A
| = 0. — ææ Ł æŁæ n
-ºŁ Ø ßı ŁØ æ n
Ł æ ß Ł (9.3)
(αE
− α
)X
= 0,
ª X
æ ºÆ Ł æ ßı. ˇ æº æ Ł Ł Œ Ł Ł ºŁ Ł -
º ª ł Ł ˛ ¸ æº , æŁæ (9.3) Ł º ł Ł X
6= 0
. º ł Ł X
∈ k
n
, Œ Œ Œ º ß -
Ł ß (αE
− A
)
Ł º º k
. ˇ æ Ł º ł Ł æŁæ (9.3) º Ł æ . ` Ł αEX
− AX
= 0,
æ AX
= αX
, ª X
6= 0 Ł X
∈ kn
. ˇ º Ł 9.6.2 Ł , α
º æ æ Ææ ß Ł Ł ß A
. 
º æ Ł
9.6.1.1.
¯æºŁ æ º k
ºª Æ Ł æŒŁ Œ , æ æ Ææ ß Ł Ł ß A
æ æ ı Œ Łæ Ł æŒŁ Ł
Œ Ł.
|