| Министерство образования Российской Федерации
Костромской государственный университет имени Некрасова
Курсовая работа
По математическому анализу
на тему: Интеграл Стилтьеса
| |
Выполнила: Бабина К. В.
Проверила: Маянская Г. М.
|
Кострома 2009
Оглавление
1.Определение интеграла Стилтьеса. 3
2.Общие условия существования интеграла Стилтьеса. 3
3.Классы случаев существования интеграла Стилтьеса. 3
4.Свойства интеграла Стилтьеса. 3
5. Интегрирование по частям. 3
6. Приведение интеграла Стилтьеса к интегралу Римана. 3
7. Вычисление интегралов Стилтьеса. 3
 Геометрическая иллюстрация интеграла Стилтьеса. 3 Геометрическая иллюстрация интеграла Стилтьеса. 3
 Теорема о среднем, оценки. 3 Теорема о среднем, оценки. 3
10. Предельный переход под знаком интеграла Стилтьеса. 3
11. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса. 3
12. Примеры. 3
Список литературы.. 3
Стилтьес Томас Иоаннес (29.21.1856, Эволле-31.12.1894, Тулуза) нидерландский ученый математик и астроном, член Нидерландской академии наук, иностранный член-корреспондент Санкт-Петербургской академии наук по Физико-математическому отделению. Окончил Политехническую школу в Делфте. Работал на Лейденской обсерватории, с 1886 года преподаватель, затем профессор Университета в Тулузе. Научные исследования Стилтьеса в основном касаются теории функциональных непрерывных дробей, проблемы моментов, теории ортогональных многочленов, интегрального преобразования, приближенного интегрирования и других вопросов классического анализа. Обобщенное Стилтьесам понятие интеграла Г.Римана, предложенное в 1894 году, играет важную роль в современной математике.
Определяется интеграл Стилтьеса следующим образом.
Пусть в промежутке [a
,
b
] заданы две ограниченные функции f
(
x
)
и g
(
x
).
Разложим точками
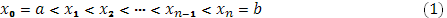
промежуток [a
,
b
] на части и положим 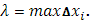 Выбрав в каждой из частей Выбрав в каждой из частей  (i
=0, 1,…,n-1) по каждой точке (i
=0, 1,…,n-1) по каждой точке 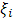 , вычислим значение f
( , вычислим значение f
(
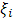 )
функции f
(
x
)
и умножим его на соответствующее промежутку )
функции f
(
x
)
и умножим его на соответствующее промежутку  приращение функции g
(
x
) приращение функции g
(
x
)
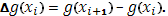
Наконец, составим сумму всех таких произведений:

Эта сумма носит название интегральной суммы Стилтьеса.
Конечный предел суммы Стилтьеса 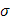 при стремлении при стремлении 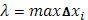 к нулю называется интегралом Стилтьеса функции f
(
x
)
по функции g
(
x
)
и обозначается символом к нулю называется интегралом Стилтьеса функции f
(
x
)
по функции g
(
x
)
и обозначается символом
Реклама

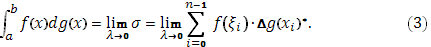
Чтобы особенно отчетливо подчеркнуть, что интеграл рассматривается в смысле Стилтьеса, употребляют обозначение
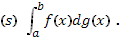
Предел здесь понимается в том смысле, что и в случае обыкновенного определенного интеграла.
Точнее говоря, число I
называется интегралом Стилтьеса, если для любого числа 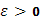 существует такое число существует такое число 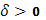 , что лишь только промежуток [a
,
b
] раздроблен на части так, что , что лишь только промежуток [a
,
b
] раздроблен на части так, что 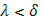 , тотчас же выполняется неравенство , тотчас же выполняется неравенство
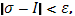
Как бы ни выбирать точки 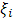 в соответствующих промежутках. в соответствующих промежутках.
При существовании интеграла (3) говорят также, что функция f
(
x
)
в промежутке [a
,
b
] интегрируема по функции 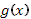 . .
Единственное (но существенное) отличие данного выше определения от обычного определения интеграла Римана состоит в том, что 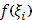 умножается не на приращение умножается не на приращение 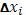 независимой переменной, а на приращение независимой переменной, а на приращение 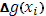 второй функции. Таким образом, интеграл Римана есть частный случай интеграла Стилтьеса, когда в качестве функции второй функции. Таким образом, интеграл Римана есть частный случай интеграла Стилтьеса, когда в качестве функции 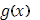 взята сама независимая переменная x
: взята сама независимая переменная x
:
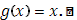
Мы для определенности предполагали a<b; нетрудно аналогично рассмотреть и случай, когда a>b. Впрочем, он непосредственно приводится к предыдущему ввиду равенства
Установим общие условия существования интеграла Стилтьеса, ограниченность, впрочем, предположением, что функция 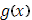 монотонно возрастает. монотонно возрастает.
Отсюда следует, что при a<b теперь все 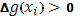 , наподобие того, как раньше было , наподобие того, как раньше было 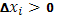 . Аналогично сумма Дарбу, здесь целесообразно ввести сумм . Аналогично сумма Дарбу, здесь целесообразно ввести сумм

где означают, соответственно, нижнюю и верхнюю точные границы функции f
(
x
)
в i
-ом промежутке  . эти суммы мы будем называть нижней и верхней суммами Дарбу - Стилтьеса. . эти суммы мы будем называть нижней и верхней суммами Дарбу - Стилтьеса.
При одном и том же разбиении 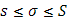 , причем s и S служат точными границами для стилтьесовых сумм , причем s и S служат точными границами для стилтьесовых сумм 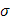 . Сами суммы Дарбу – Стилтьеса обладают следующими свойствами: . Сами суммы Дарбу – Стилтьеса обладают следующими свойствами:
1-е свойство: Если к имеющимся точкам деления добавить новые точки, то нижняя сумма Дарбу – Стилтьеса может от этого разве лишь возрасти, а верхняя сумма – разве лишь уменьшится.
2-е свойство: Каждая нижняя сумма Дарбу – Стилтьеса не превосходит каждой верхней суммы, хотя бы и отвечающей другому разбиению промежутка.
Если ввести нижний и верхний интегралы Дарбу – Стилтьеса:
то оказывается, что
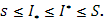
Наконец, с помощью сумм Дарбу – Стилтьеса легко устанавливается для рассматриваемого случая основной признак существования интеграла Стилтьеса:
Теорема. Для существования интеграла Стилтьеса необходимо и достаточно, чтоб было
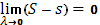
или

если под 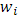 понимать колебание понимать колебание 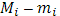 функции f
(
x
)
в i
-ом промежутке функции f
(
x
)
в i
-ом промежутке 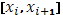 . .
Реклама

Определение функции с ограниченным изменением:
Пусть функция f
(
x
)
определена в некотором конечном промежутке [a
,
b
]. Разложим этот промежуток произвольным образом на части с помощью точек деления:
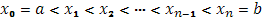
Из абсолютных величин приращений функции, отвечающих отдельным частичным промежуткам, образуем сумму
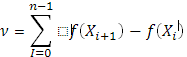
Если такие суммы в их совокупности ограничены сверху, то говорят, что функция f
(
x
)
в промежутке [a
,
b
] имеет ограниченное изменение ( или ограниченную вариацию). При этом точную верхниюю границу этих сумм называют полным изменением функции в указанном промежутке и обозначают символом
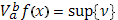
I
. Если функция f
(
x
)
непрерывна, а функция 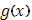 имеет ограниченное изменение, то интеграл Стилтьеса имеет ограниченное изменение, то интеграл Стилтьеса

существует.
Сначала предположим, что 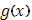 монотонно возрастает: тогда применим критерий предыдущего пункта. По произвольному заданию монотонно возрастает: тогда применим критерий предыдущего пункта. По произвольному заданию  ввиду равномерной непрерывности функции f
(
x
)
найдется такое ввиду равномерной непрерывности функции f
(
x
)
найдется такое 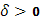 , что в любом промежутке с длиной, меньшей , что в любом промежутке с длиной, меньшей 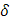 , колебание f
(
x
)
будет меньше , колебание f
(
x
)
будет меньше 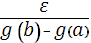 . Пусть теперь промежуток [a
,
b
] произвольно разбит на части так, что . Пусть теперь промежуток [a
,
b
] произвольно разбит на части так, что 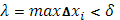 . Тогда все . Тогда все 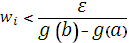 и и
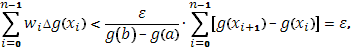
откуда и следует выполнение условия (4), а стало быть и существование интеграла.
В общем случаи, если функция 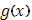 имеет ограниченное изменение, она представима в виде разности двух ограниченных возрастающих функций: имеет ограниченное изменение, она представима в виде разности двух ограниченных возрастающих функций: 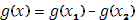 . В соответствии с этим преобразуется и сумма Стилтьеса, отвечающая функции . В соответствии с этим преобразуется и сумма Стилтьеса, отвечающая функции 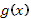 : :
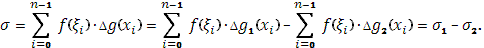
Так как каждая из сумм 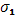 и и 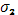 при при 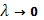 стремится к конечному пределу, то это справедливо и относительно суммы стремится к конечному пределу, то это справедливо и относительно суммы 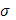 , что и требовалось доказать. , что и требовалось доказать.
Можно ослабить условия, налагаемые на функцию f
(
x
),
если одновременно усилить требования к функции 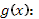
II
. Если функция f
(
x
)
интегрируема в [a
,
b
] в смысле Римана, а 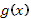 удовлетворяет условию Липшица: удовлетворяет условию Липшица:
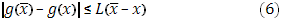
(L=const., 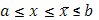 ), то интеграл существует. ), то интеграл существует.
Предположим, что функция 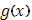 не только удовлетворяет условию (6), но и является монотонно возрастающей. не только удовлетворяет условию (6), но и является монотонно возрастающей.
Ввиду (6), очевидно, 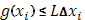 , так что , так что
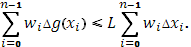
Но последняя сумма при 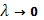 и сама стремится к 0 вследствие интегрируемости (в смысле Римана) функции f
(
x
)
, а тогда стремится к нулю и первая сумма, что доказывает существование интеграла (5). и сама стремится к 0 вследствие интегрируемости (в смысле Римана) функции f
(
x
)
, а тогда стремится к нулю и первая сумма, что доказывает существование интеграла (5).
В общем случаи функции 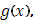 удовлетворяющей условию Липшица (6), представим ее в виде разности удовлетворяющей условию Липшица (6), представим ее в виде разности
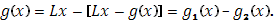
Функция 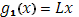 , очевидно, удовлетворяет условию Липшица и в то же время монотонно возрастает. То же справедливо и для функции , очевидно, удовлетворяет условию Липшица и в то же время монотонно возрастает. То же справедливо и для функции 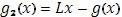 , так как, в силу (6) , при , так как, в силу (6) , при 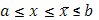
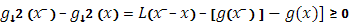
и

III
.
Если функция f
(
x
) интегрируема в смысле Римана, а функция 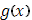 представима в виде интеграла с переменным верхним пределом: представима в виде интеграла с переменным верхним пределом:

где 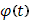 абсолютно интегрируема в промежутке [a
,
b
], то интеграл (5) существует. абсолютно интегрируема в промежутке [a
,
b
], то интеграл (5) существует.
Пусть 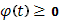 , так что монотонно возрастает. Если , так что монотонно возрастает. Если 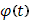 интегрируема в собственном смысле и, следовательно, ограничена: интегрируема в собственном смысле и, следовательно, ограничена:
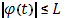 ,
то для ,
то для имеем имеем
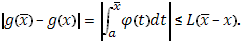
Таким образом, в этом случаи 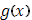 удовлетворяет условию Липшица, и интеграл существует в силу II. удовлетворяет условию Липшица, и интеграл существует в силу II.
Предположим теперь, что 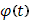 интегрируема в несобственном смысле. Ограничимся случаем одной особой точки, например, b
. Прежде всего, т.к. интегрируема в несобственном смысле. Ограничимся случаем одной особой точки, например, b
. Прежде всего, т.к. 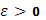 выберем выберем 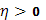 так, чтобы было так, чтобы было

где 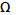 - общее колебание функции - общее колебание функции 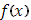 в рассматриваемом промежутке. в рассматриваемом промежутке.
Разобьем промежуток [a
,
b
] произвольным образом на части и составим сумму

Она распадается на две суммы 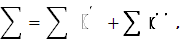 из которых первая отвечает промежуткам, целиком содержащимся в промежутке из которых первая отвечает промежуткам, целиком содержащимся в промежутке 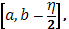 а вторая – остальным промежуткам. Последнее содержатся в промежутке [b
- а вторая – остальным промежуткам. Последнее содержатся в промежутке [b
-
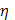 ,
b
], если только ,
b
], если только 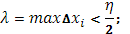 тогда, в силу (8), тогда, в силу (8),
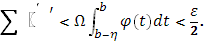
С другой стороны, так как в промежутке 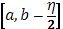 функция функция 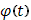 интегрируема в собственном смысле, то по доказанному при достаточно малом интегрируема в собственном смысле, то по доказанному при достаточно малом 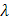 и сумма и сумма 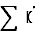 станет меньше станет меньше 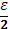 . Отсюда следует (4), что и требовалось доказать. . Отсюда следует (4), что и требовалось доказать.
В общем случаи, когда функция 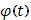 абсолютно интегрируема в промежутке [a
,
b
]: абсолютно интегрируема в промежутке [a
,
b
]:

неотрицательные и интегрируемые в названном промежутке. Так как
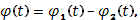
то вопрос сводится, как и выше, к уже рассмотренному случаю.
Замечание. Пусть функция 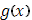 непрерывна в промежутке [a
,
b
] и имеет, исключая лишь конечное число точек, производную непрерывна в промежутке [a
,
b
] и имеет, исключая лишь конечное число точек, производную 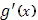 , причем эта производная (если ее значения в точках, где она не существует, выбрать произвольным образом) интегрируема (в собственном или несобственном смысле) от a
до b
; тогда имеет место формула типа (7): , причем эта производная (если ее значения в точках, где она не существует, выбрать произвольным образом) интегрируема (в собственном или несобственном смысле) от a
до b
; тогда имеет место формула типа (7):
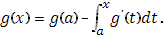
Если 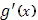 абсолютно интегрируема, то к функции абсолютно интегрируема, то к функции 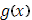 полностью приложимо изложенное в III. полностью приложимо изложенное в III.
Из определения интеграла Стилтьеса непосредственно вытекают следующие свойства:



Доказательство:
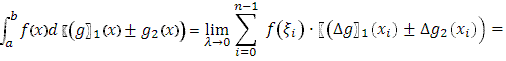
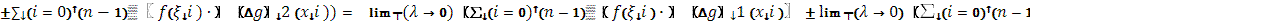
=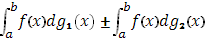
Что и требовалось доказать.

При этом в случаях 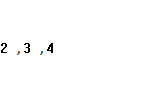 из существования интегралов в правой части вытекает существование интеграла в левой части. из существования интегралов в правой части вытекает существование интеграла в левой части.
Затем имеем

в предложении, что a
<
c
<
b
и существуют все три интеграла.
Для доказательства этой формулы достаточно включить точку с
в число точек деления промежутка [a
,
b
] при составлении суммы Стилтьеса для интеграла 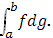
Из существования интеграла 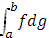 следует существование обоих интегралов следует существование обоих интегралов 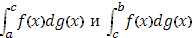 . .
Для своеобразного предельного процесса, с помощью которого
из стилтьесовой суммы получается интеграл Стилтьеса, имеет
место принцип сходимости Больцано–Коши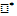 . Таким образом, по заданному . Таким образом, по заданному 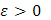 ввиду существования интеграла ввиду существования интеграла 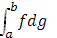 найдется такое найдется такое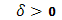 , что любые две суммы , что любые две суммы 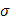 и и 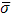 Стилтьеса, которым отвечают Стилтьеса, которым отвечают 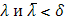 разнятся меньше чем на разнятся меньше чем на 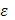 . Если при этом в состав точек деления включить точку с, а точки деления, приходящиеся на промежуток [с, b], брать в обоих случаях одними и теми же, то разность( . Если при этом в состав точек деления включить точку с, а точки деления, приходящиеся на промежуток [с, b], брать в обоих случаях одними и теми же, то разность( 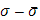 ) сведется к разности( ) сведется к разности(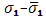 ) двух сумм Стилтьеса , относящихся уже к промежутку [а, с], ибо прочие слагаемые взаимно уничтожатся. Применяя к промежутку [a, с] и вычисленным для него стилтьесовым суммам тот же принцип сходимости, заключим о существовании интеграла ) двух сумм Стилтьеса , относящихся уже к промежутку [а, с], ибо прочие слагаемые взаимно уничтожатся. Применяя к промежутку [a, с] и вычисленным для него стилтьесовым суммам тот же принцип сходимости, заключим о существовании интеграла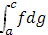 . Аналогично устанавливается и существование интеграла . Аналогично устанавливается и существование интеграла 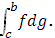
Надо отметить что из существования обоих интегралов 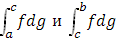 , вообще говоря, не вытекает существование интеграла , вообще говоря, не вытекает существование интеграла 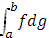 . .
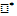 Теорема(
Больцано–Коши
).
Для того чтобы функция
f
(
x
) при стремлении
x
к а имела конечный предел ,т.е. сходилась, необходимо и достаточно, чтобы для каждого числа Теорема(
Больцано–Коши
).
Для того чтобы функция
f
(
x
) при стремлении
x
к а имела конечный предел ,т.е. сходилась, необходимо и достаточно, чтобы для каждого числа
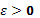 существовало такое число существовало такое число
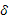 >0
, чтобы неравенство
\
f
(
x
)-
f
(
x
')\ >0
, чтобы неравенство
\
f
(
x
)-
f
(
x
')\
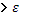 выполнялось, лишь только выполнялось, лишь только

Для интегралов Стилтьеса имеет место формула
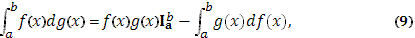
в предположении, что существует один из этих интегралов. Формула эта носит название формулы интегрирования по частям.
Доказательство:
Пусть существует интеграл 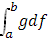 . Разложим промежуток [a
,
b
] на части . Разложим промежуток [a
,
b
] на части 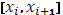 (i
=0, 1, …,
n
-1
), выберем в этих частях произвольно (i
=0, 1, …,
n
-1
), выберем в этих частях произвольно 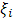 , так что , так что
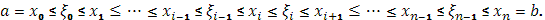
Сумму Стилтьеса для интеграла 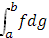
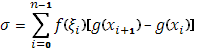
можно представить в виде
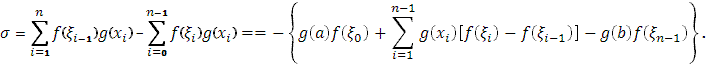
Если прибавить и отнять справа выражение
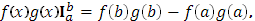
то 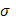 перепишется так: перепишется так:
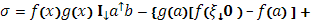

Выражение в фигурных скобках представляет собою стилтьесову сумму для интеграла 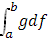 (существование которого предположено!). Она отвечает разбиению промежутка [a
,
b
] точками деления (существование которого предположено!). Она отвечает разбиению промежутка [a
,
b
] точками деления
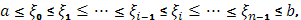
если в качестве выбранных из промежутков 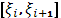 (i
= 1, …,
n
-1
) точек взять (i
= 1, …,
n
-1
) точек взять 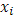 , а для промежутков [
a
, , а для промежутков [
a
,
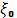 ] и [ ] и [
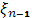 ,
b
]
, соответственно, a
и b
. Если положить ,
b
]
, соответственно, a
и b
. Если положить 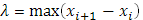 , то теперь длины всех частичных промежутков не превзойдут 2 , то теперь длины всех частичных промежутков не превзойдут 2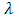 . При . При 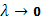 сумма в квадратных скобках стремится к сумма в квадратных скобках стремится к 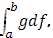 следовательно, существует предел следовательно, существует предел 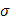 , т.е. интеграл , т.е. интеграл 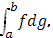 и этот интеграл определяется формулой (9). и этот интеграл определяется формулой (9).
Если функция g
(
x
)
в промежутке [a
,
b
] интегрируема по функции f
(
x
),
то и функция f
(
x
)
интегрируема по функции g
(
x
).
 Пусть функция f
(
x
)
непрерывна в промежутке [a
,
b
], а g
(
x
)
монотонно возрастает в этом промежутке, и притом в строгом смысле (для упрощения). Тогда, как показал Лебег, интеграл Стилтьес Пусть функция f
(
x
)
непрерывна в промежутке [a
,
b
], а g
(
x
)
монотонно возрастает в этом промежутке, и притом в строгом смысле (для упрощения). Тогда, как показал Лебег, интеграл Стилтьес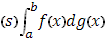 а с помощью подстановки а с помощью подстановки 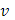 =
g
(
x
)
непосредственно приводится к интегралу Римана. =
g
(
x
)
непосредственно приводится к интегралу Римана.
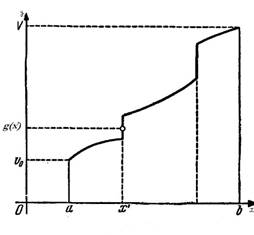
На рисунке изображен график функции 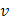 =
g
(
x
)
. Для тех значений x
=
x
’,
при которых функция g
(
x
)
испытывает скачок, дополним график прямолинейным вертикальным отрезком, соединяющим точки (x
’,
g
(
x
’-0)
) и (x
’,
g
(
x
’+0
)). Так создается непрерывная линия, которая каждому значению v
между =
g
(
x
)
. Для тех значений x
=
x
’,
при которых функция g
(
x
)
испытывает скачок, дополним график прямолинейным вертикальным отрезком, соединяющим точки (x
’,
g
(
x
’-0)
) и (x
’,
g
(
x
’+0
)). Так создается непрерывная линия, которая каждому значению v
между 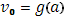 и V
=
g
(
b
)
относит одно определенное значение x
между a
и b
. Эта функция и V
=
g
(
b
)
относит одно определенное значение x
между a
и b
. Эта функция 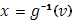 будет непрерывной и монотонно возрастающей в широком смысле; ее можно рассматривать как своего рода обратную для функции будет непрерывной и монотонно возрастающей в широком смысле; ее можно рассматривать как своего рода обратную для функции 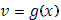 . .
Именно, если ограничиться лишь теми значениями 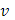 , которые функция , которые функция 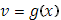 действительно принимает при изменении действительно принимает при изменении 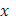 от a
до b
,
то от a
до b
,
то 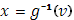 является обратной для нее в обычном смысле, т.е. относит является обратной для нее в обычном смысле, т.е. относит 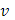 именно те значения именно те значения 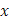 , при которых , при которых 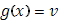 . Но из промежутка значений . Но из промежутка значений 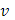 [
g
(
x
’-0),
g
(
x
’+0)]
, связанного со скачком функции [
g
(
x
’-0),
g
(
x
’+0)]
, связанного со скачком функции 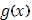 , лишь одно значение , лишь одно значение  имеет себе соответствующим значение имеет себе соответствующим значение 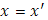 ; другим значениям ; другим значениям 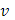 в упомянутом промежутке никакие значения в упомянутом промежутке никакие значения 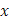 не отвечают. Условно относим и им то же значение не отвечают. Условно относим и им то же значение 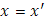 ; геометрически это и выразилось в дополнении графика функции ; геометрически это и выразилось в дополнении графика функции 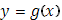 рядом вертикальных отрезков. рядом вертикальных отрезков.
Теперь докажем:
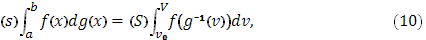
где последний интеграл берется в обычном смысле, его существование обеспечено, так как функция 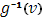 , а с нею и сложная функция , а с нею и сложная функция 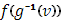 , непрерывна. , непрерывна.
С этой целью разложим промежуток [a
,
b
] на части с помощью точек деления
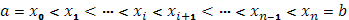
и составим стилтьесову сумму
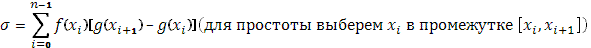
Если предположить 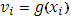 (i
=0, 1, …,
n
), то будем иметь (i
=0, 1, …,
n
), то будем иметь
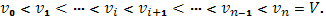
Так как 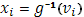 , то , то
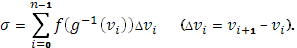
Это выражение имеет вид римановой суммы для интеграла
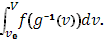
Отсюда, однако, нельзя еще непосредственно заключить, переходя к пределу, о равенстве (10), ибо даже при 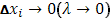 может оказаться, что может оказаться, что 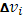 к нулю не стремится. Тогда имеем к нулю не стремится. Тогда имеем
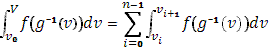
и
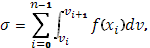
так что
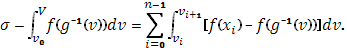
Предположим теперь 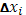 настолько малым, чтобы колебания функции настолько малым, чтобы колебания функции 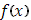 во всех промежутках во всех промежутках 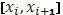 были меньше произвольного наперед заданного числа были меньше произвольного наперед заданного числа 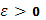 . Так как при . Так как при 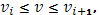 очевидно, очевидно, 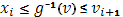
То одновременно и 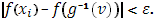 В таком случаи В таком случаи
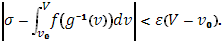
Этим доказано, что
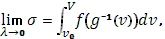
откуда и следует (10).
 Если функция Если функция 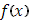 интегрируема в смысле Римана в промежутке интегрируема в смысле Римана в промежутке 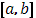 , а , а 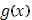 представлена интегралом представлена интегралом

где функция 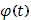 абсолютн абсолютн интегрируема в интегрируема в 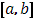 , то , то
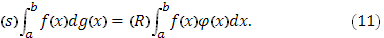
Интеграл справа существует. Существование Стилтьеса было уже доказано в п.3 (III). Остается лишь установить равенство (11).
Предположим, что 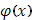 - положительная функция (для упрощения). - положительная функция (для упрощения).
Составим сумму Стилтьеса
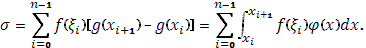
Так как, с другой стороны, можно написать
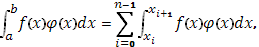
то будем иметь
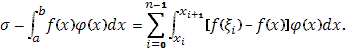
Очевидно, для 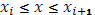 будет будет 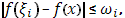 где где 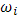 - это колебание функции - это колебание функции 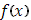 в промежутке в промежутке 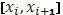 . Отсюда выкает оценка написанной выше разности: . Отсюда выкает оценка написанной выше разности:
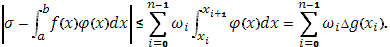
Т.к. в п.3 (III) мы доказали, что при 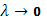  стремится к 0, следовательно стремится к 0, следовательно
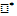 Если с интегралом Если с интегралом 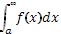 сходится и интеграл сходится и интеграл 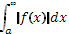 ,
то интеграл ,
то интеграл 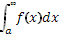 называют абсолютно сходящимся,
а функцию fix
) - аб
солютно интегрируемой
в промежутке [а, + называют абсолютно сходящимся,
а функцию fix
) - аб
солютно интегрируемой
в промежутке [а, +
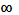 ] ]
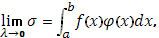
что и доказывает формулу (11).
 При прежних предложениях относительно функции При прежних предложениях относительно функции 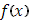 допустим, что функция допустим, что функция 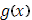 непрерывна во всем промежутке непрерывна во всем промежутке 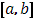 и имеем, исключая разве лишь конечное число точек, производную и имеем, исключая разве лишь конечное число точек, производную 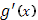 , которая в , которая в 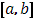 абсолютно интегрируема. Тогда абсолютно интегрируема. Тогда
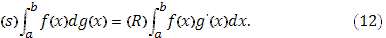
Интеграл справа в формуле (12) формально получается из интеграла слева, если, понимая символ 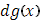 буквально как дифференциал, заменить его выражением буквально как дифференциал, заменить его выражением 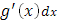 . .
Если функция 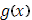 оказывается разрывной, то начнем с рассмотрения «стандартной» разрывной функции оказывается разрывной, то начнем с рассмотрения «стандартной» разрывной функции 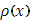 , определяемой равенствами , определяемой равенствами
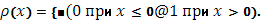
Она имеет разрыв первого рода - скачок - в точке x=0 справа, причем величина скачка 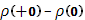 равна 1; в точке x=0 слева и в остальных точках функции равна 1; в точке x=0 слева и в остальных точках функции 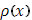 непрерывна. Функция непрерывна. Функция 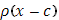 будет иметь такой же разрыв в точке x=c справа; наоборот, будет иметь такой же разрыв в точке x=c справа; наоборот, 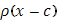 будет иметь подобный разрыв в точке x=c слева, причем величина скачка будет равна -1. будет иметь подобный разрыв в точке x=c слева, причем величина скачка будет равна -1.
Предположим, что функция 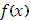 непрерывна в точке x=c, и вычислим интеграл непрерывна в точке x=c, и вычислим интеграл
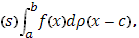
где 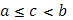 при (c=b этот интеграл равен нулю). при (c=b этот интеграл равен нулю).
Составим сумму Стилтьеса:
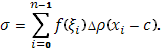
Пусть точка c попадет в k
-й промежуток, так что 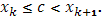 Тогда Тогда 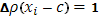 , а при , а при 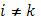  . Таким образом, вся сумма . Таким образом, вся сумма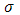 сводится к одному слагаемому: сводится к одному слагаемому: 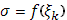 . Пусть теперь . Пусть теперь 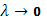 . По непрерывности . По непрерывности 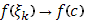 . Следовательно, существует (при . Следовательно, существует (при 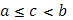 ) )
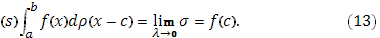
Аналогично можно убедиться в том, что (при ) )
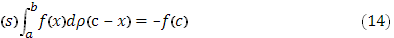
(при c=a этот интеграл обращается в нуль).
Пусть функция 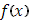 в промежутке в промежутке 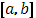 непрерывна, а непрерывна, а 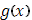 имеет в этом промежутке, исключая разве лишь конечное число точек, производную имеет в этом промежутке, исключая разве лишь конечное число точек, производную 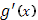 , которая абсолютно интегрируема в , которая абсолютно интегрируема в 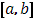 . При этом пусть функция . При этом пусть функция 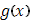 в конечном числе точек в конечном числе точек
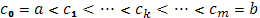
Терпит разрыв первого рода. Тогда существует интеграл Стилтьеса и выражается формулой
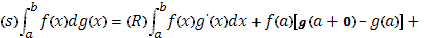
Характерно здесь наличие внеинтегральной суммы, где фигурируют скачки функции 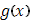 в точках a
или b
– односторонние (если на деле какой-либо из этих точек скачка нет, то соответствующее слагаемое суммы обращается в нуль). в точках a
или b
– односторонние (если на деле какой-либо из этих точек скачка нет, то соответствующее слагаемое суммы обращается в нуль).
Для упрощения записи введем обозначения для скачков функции 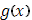 справа и слева: справа и слева:
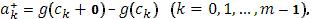
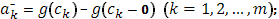
очевидно, для 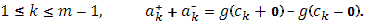
Составим вспомогательную функцию:
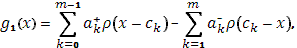
которая как бы вбирает в себя все разрывы функции 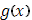 , так что разность , так что разность 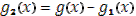 оказывается непрерывной (по доказанному ранее). оказывается непрерывной (по доказанному ранее).
Для значений 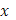 , отличных от всех , отличных от всех 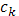 , непрерывность функции , непрерывность функции 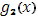 не вызывает сомнений, т.к. для этих значений непрерывны обе функции не вызывает сомнений, т.к. для этих значений непрерывны обе функции 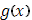 и и 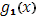 . Докажем непрерывность . Докажем непрерывность 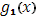 в точке в точке 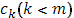 справа. Все слагаемые суммы справа. Все слагаемые суммы 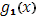 , кроме члена , кроме члена 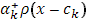 , непрерывны при , непрерывны при 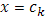 справа; поэтому достаточно изучить поведение выражения справа; поэтому достаточно изучить поведение выражения 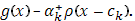 При При 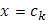 оно имеет значение оно имеет значение 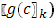 ; но таков же и предел при ; но таков же и предел при 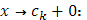
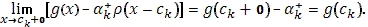
Аналогично проверяется и непрерывность функции 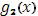 в точке в точке 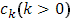 слева. слева.
Далее, если взять точку 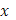 (отличную от всех (отличную от всех 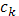 ), в которой функция ), в которой функция 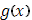 имеет производную, то вблизи этой точки имеет производную, то вблизи этой точки 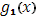 сохраняет постоянное значение, следовательно, в ней и функция сохраняет постоянное значение, следовательно, в ней и функция 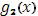 имеет производную, причем имеет производную, причем 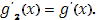
Для непрерывности функции 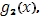 по предыдущей теореме, существует интеграл Стилтьеса по предыдущей теореме, существует интеграл Стилтьеса
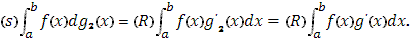
Точно так же легко вычислить и интеграл (с учетом (13), (14))
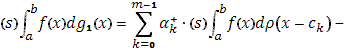
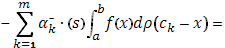

Складывая почленно эти два равенства, придем к равенству (15); существование интеграла Стилтьеса от 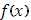 по функции по функции
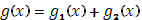 устанавливается попутно свойство устанавливается попутно свойство 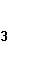 в п.4. в п.4.
 Геометрическая иллюстрация интеграла Стилтьеса. Геометрическая иллюстрация интеграла Стилтьеса.
Рассмотрим интеграл

предполагая функцию 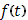 непрерывной и положительной а непрерывной и положительной а 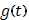 -монотонно возрастающей (в строгом смысле); функция -монотонно возрастающей (в строгом смысле); функция 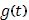 может иметь и разрывы (скачки). может иметь и разрывы (скачки).
Система параметрических уравнений 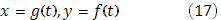
выражает некоторую кривую (K
) , разрывную, как на рисунке.
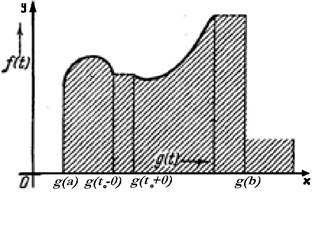 Если при некотором Если при некотором 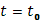 функция функция 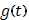 испытывает скачок, так что испытывает скачок, так что 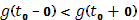 , то этим предельным значениям , то этим предельным значениям 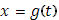 отвечает одно и то же предельное значение отвечает одно и то же предельное значение 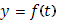 , равное , равное 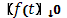 ). Дополним кривую (K
) всем горизонтальным отрезками, соединяющими пары точек ). Дополним кривую (K
) всем горизонтальным отрезками, соединяющими пары точек
отвечающие всем скачкам функции 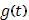 (по рисунку). Таким образом, составится уже непрерывная кривая (L
). Покажем, что интеграл (16) представляет площадь фигуры под этой кривой, т.е. площадь фигуры, ограниченной кривой (L
), осью x
и двумя крайними ординатами, отвечающими абсциссам (по рисунку). Таким образом, составится уже непрерывная кривая (L
). Покажем, что интеграл (16) представляет площадь фигуры под этой кривой, т.е. площадь фигуры, ограниченной кривой (L
), осью x
и двумя крайними ординатами, отвечающими абсциссам 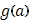 и и 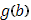 . .
С этой целью разложим промежуток 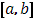 на части точками на части точками
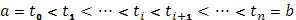
и в соответствии с этим промежуток 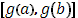 на оси на оси 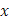 - на части точками - на части точками
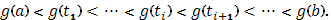
Введя наименьшее и наибольшее значения 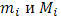 функции функции 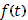 в i
-ом промежутке в i
-ом промежутке 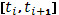 , составим нижнюю и верхнюю суммы Стилтьеса – Дарбу , составим нижнюю и верхнюю суммы Стилтьеса – Дарбу
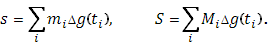
Они представляют площади фигур, составленных из входящих и из выходящих прямоугольников, между которыми содержится рассматриваемая криволинейная фигура.
Так как при стремлении в 0 всех 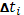 обе суммы стремятся к общему пределу (16), то отсюда следует, что фигура, изображенная на рисунке квадрируема и площадью ее служит действительно интеграл (16). обе суммы стремятся к общему пределу (16), то отсюда следует, что фигура, изображенная на рисунке квадрируема и площадью ее служит действительно интеграл (16).
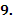 Теорема о среднем, оценки. Теорема о среднем, оценки.
 Пусть в промежутке Пусть в промежутке 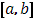 функция функция 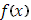 ограничена: ограничена: 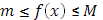 , а , а 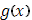 монотонно возрастает. Если существует интеграл Стилтьеса монотонно возрастает. Если существует интеграл Стилтьеса 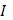 от от 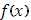 и и 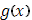 , то имеет место формула , то имеет место формула
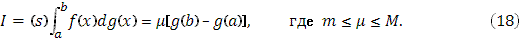
То есть это теорема о среднем для интегралов Стилтьеса.
Доказательство:
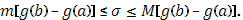
Переходя к пределу, получим

Возьмем 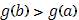 , т.к. случай , т.к. случай 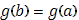 (т.е. (т.е. 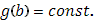 ) не представляет интереса: обе части формулы (18) – нули. ) не представляет интереса: обе части формулы (18) – нули.
Тогда
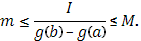
Обозначая написанное отношение через 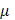 и придем к (18). и придем к (18).
Если 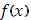 в промежутке в промежутке 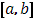 непрерывна, тогда непрерывна, тогда  и есть значение функции в некоторой точке этого промежутка, и формула (18) имеет вид и есть значение функции в некоторой точке этого промежутка, и формула (18) имеет вид
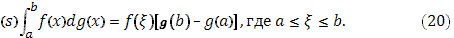
 Пусть Пусть 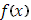 непрерывна, а функция непрерывна, а функция 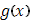 имеет ограниченное изменение. Для этого случая справедлива оценка интеграла Стилтьеса: имеет ограниченное изменение. Для этого случая справедлива оценка интеграла Стилтьеса:

где 
Доказательство:
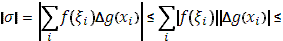
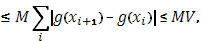
так что остается лишь перейти к пределу, чтобы получить (21).
 Пусть в промежутке Пусть в промежутке 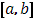 функция функция 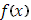 ограничена, ограничена, 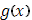 монотонно возрастает. Если существует интеграл Стилтьеса монотонно возрастает. Если существует интеграл Стилтьеса 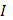 от от 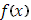 и и 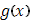 , то имеет место формула , то имеет место формула
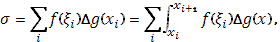
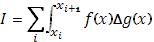
и почленно вычитая эти равенства, получим
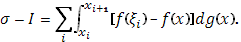
Обозначим через 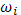 колебание функции колебание функции 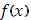 в промежутке в промежутке 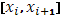 , тогда , тогда
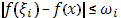 для для 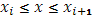 , то, применяя оценку (21) к каждому интегралу с границами , то, применяя оценку (21) к каждому интегралу с границами 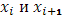 в отдельности, получаем: в отдельности, получаем:
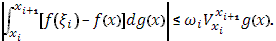
Если промежуток 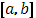 раздроблен на столь мелкие части, что все раздроблен на столь мелкие части, что все 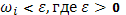 – произвольное наперед заданное взятое число, тогда – произвольное наперед заданное взятое число, тогда

 Пусть функции Пусть функции 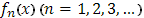 непрерывны в промежутке непрерывны в промежутке  и при и при 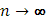 равномерно стремятся к предельной функции равномерно стремятся к предельной функции
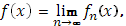
также непрерывной, а 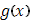 - функция с ограниченным изменением. Тогда - функция с ограниченным изменением. Тогда
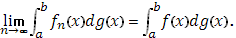
Доказательство:
По заданному 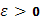 найдется такое N
, что при n
>
N
будет для всех x найдется такое N
, что при n
>
N
будет для всех x
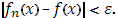
Тогда в силу (21), для n
>
N
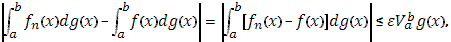
т.к. 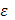 - произвольное, то теорема доказана. - произвольное, то теорема доказана.
 Пусть функция Пусть функция 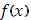 непрерывна в промежутке непрерывна в промежутке  , а функция , а функция 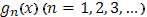 - все с ограниченным изменением в этом промежутке. Если полные изменения этих функций в их совокупности ограничены: - все с ограниченным изменением в этом промежутке. Если полные изменения этих функций в их совокупности ограничены:
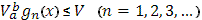
и 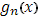 при при 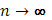 стремятся к предельной функции стремятся к предельной функции
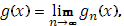
то
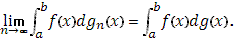
Доказательство:
Докажем, что 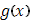 имеет ограниченное изменение. Разложим промежуток имеет ограниченное изменение. Разложим промежуток  произвольным образом на части точками произвольным образом на части точками
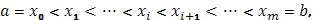
Тогда для любого 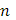
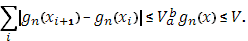
Перейдем к пределу при 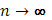
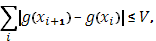
откуда и
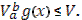
Составим суммы Стилтьеса
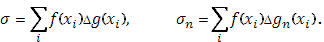
Если предположить, что промежуток 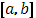 при этом разложен на столь мелкие части, что колебание функции при этом разложен на столь мелкие части, что колебание функции 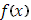 в каждой из них будет уже меньше произвольного наперед взятого числа в каждой из них будет уже меньше произвольного наперед взятого числа 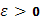 , то, в силу оценки (22), при всех , то, в силу оценки (22), при всех 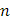
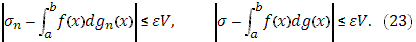
С другой стороны, если разбиение фиксировать, то, очевидно, 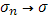 при при 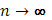 , так что найдется такое N
,
что для n
>
N
будет , так что найдется такое N
,
что для n
>
N
будет

Тогда для тех же значений n
в силу (23) и (24) получаем:
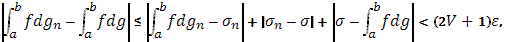
Т.к. 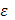 - любое, то теорема доказана. - любое, то теорема доказана.
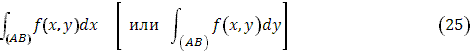
Пусть кривая 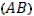 задана параметрическими уравнениями задана параметрическими уравнениями

в направлении от 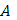 к к 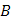 , когда , когда 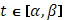 . Тогда точкам . Тогда точкам 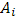 ( (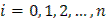 ), взятым на кривой для образования интегральной суммы, будут отвечать возрастающие значения параметра ), взятым на кривой для образования интегральной суммы, будут отвечать возрастающие значения параметра 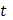 : :
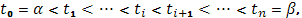
а выбранной на дуге 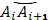 точке точке 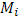 – значение – значение 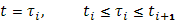
(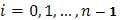 ). Сама же интегральная сумма, например, для первого из интегралов, напишется в виде ). Сама же интегральная сумма, например, для первого из интегралов, напишется в виде
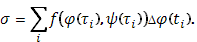
Эта интегральная сумма представляет собою стилтьесову сумму, так что криволинейный интеграл второго типа по самому определению отождествляется с частным случаем интеграла Стилтьеса:
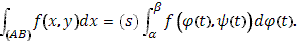
Аналогично и
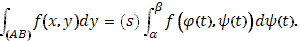
Отсюда следуют общие условия существования криволинейного интеграла (25); достаточно предположить функцию 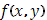 непрерывной, а функцию непрерывной, а функцию 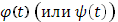 имеющей ограниченное изменение (п.3, имеющей ограниченное изменение (п.3,  ). ).
В частности, если кривая AB
спрямляема, а функции P
(
x
,
y
)
и Q
(
x
,
y
)
непрерывны, то существует интеграл
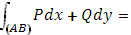
№1
Вычислить по формуле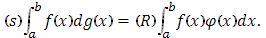
а)
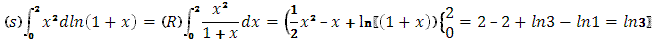
б
)
(s)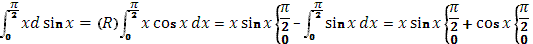
=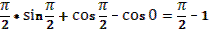
в)(s)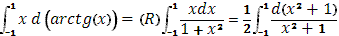 = =
№2
Вычислить по формуле 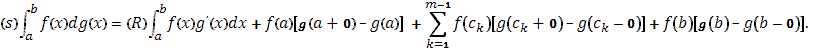
а)
(S)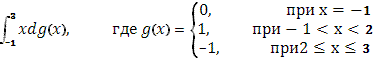
функция g(x) терпит скачок 1, при х=-1
скачок -2, при х=2
в остальных точках 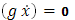 , т.к. g(x)=const , т.к. g(x)=const
(S)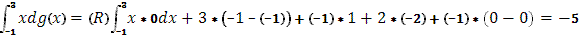
б
) (
S)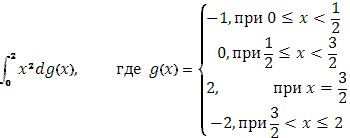
функция g(x) терпит скачок 1, при х=
скачок -2, при х=
в остальных точках 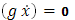 , т.к. g(x)=const , т.к. g(x)=const
(S)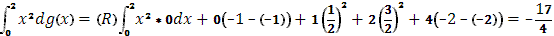
№
3 Вычислить по формуле 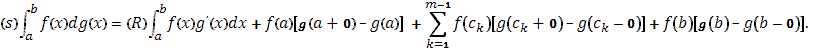 При При 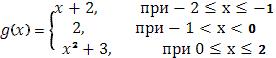
а)
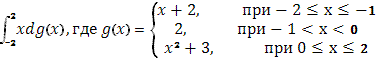
функция g(x) терпит скачок 1, при х=-1
скачок 1, при х=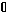
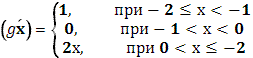
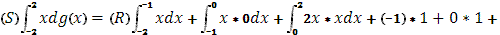
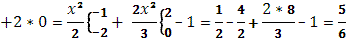
б)
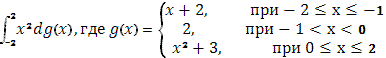
функция g(x) терпит скачок 1, при х=-1
скачок 1, при х=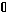
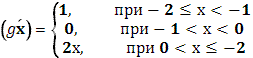
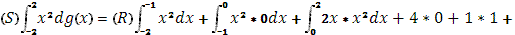
+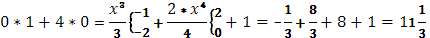
в)
функция g(x) терпит скачок 1, при х=-1
скачок 1, при х=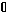
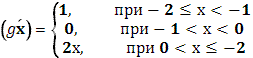
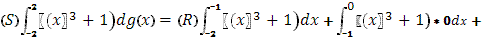
+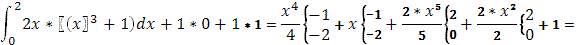
=
№4
а)
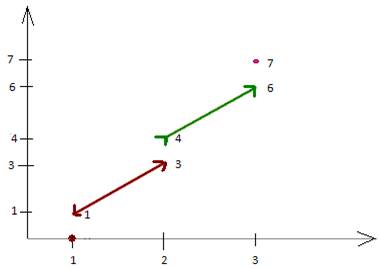
Составить выражение Ф(х) и построить график его для следующего распределения масс: массы величины 1 в точках х= 1, 2 и 3 и непрерывно распределенные массы с плотностью 2 в промежутке [1;3]
Решение.
Ф(х)=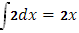
Ф(а)=о => Ф(1)=0
В точке х=1 функция терпит скачок =1 => Ф(х)=2х-1
В точке х=2 функция терпит скачок =1 => Ф(х)=2х
В точке х=3 функция терпит скачок =1 => Ф(х)=2*3+1=7
Итого:
Ф(х)=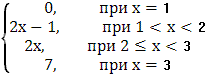
б)
Составить выражение Ф(х) для следующего распределения масс: массы величины 2 в точках х= 2 и 4 и непрерывно распределенные массы с плотностью 2х в промежутке [0;5]
Решение.
Ф(х)=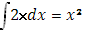
Ф(а)=о => Ф(1)=0
В точке х=2 функция терпит скачок =2 => Ф(х)=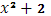
В точке х=4 функция терпит скачок =2 => Ф(х)=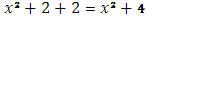
Итого:
Ф(х)=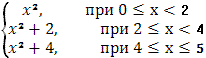
в)
Выяснить распределение масс, если Ф(х)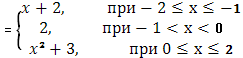
Решение.
При х=-1 и 0 функция испытывает скачок =1 => массы величины 1 в точках х=-1 и 0, в промежутке [-2,-1] непрерывно распределенные массы с плотностью 1, т.к. , в промежутке [0,2] непрерывно распределенные массы с плотностью 2х, т.к.
1. Г. М. Фихтенгольц. Курс дифференциального и интегрального исчисления. Том 3.Москва 1960
2. http://www.phismat.ru/dif.php
|