| Министерство образования и науки РФ
Государственное образовательное учреждение высшего профессионального образования
«Кубанский государственный технологический университет»
Реферат
Тема: Основные понятия и уравнения термодинамики. Первое и второе начало термодинамики. Энтропия.
Выполнил: ст. гр. 09-Н-РЭ1
Гавриленко В.С.
Краснодар
2010г.

СОДЕРЖАНИЕ
ВВЕДЕНИЕ
ГЛАВА 1
ОСНОВНЫЕ ПОНЯТИЯ И ИСХОДНЫЕ ПОЛОЖЕНИЯ ТЕРМОДИНАМИКИ
1.1.
Закрытые и открытые термодинамические системы.
1.2.
Нулевое начало термодинамики.
1.3.
Первое начало термодинамики.
1.4.
Второе начало термодинамики.
1.4.1.
Обратимые и необратимые процессы.
1.4.2.
Энтропия.
Третье начало термодинамики.
ГЛАВА 2
ИЗОПРОЦЕССЫ В ГАЗАХ
| 2.1. Уравнение состояние идеального газа
|
| 2.2 Изотермический процесс
|
| 2.3. Изобарический процесс
|
| 2.4. Изохорический процесс
|
| 2.5. Адиабатический процесс
|
ЛИТЕРАТУРА
ВВЕДЕНИЕ.
Наука зародилась очень давно, на Древнем Востоке, и затем интенсивно развивалась в Европе. В научных традициях долгое время оставался недостаточно изученным вопрос о
взаимоотношениях целого и части. Как стало ясно в середине
20 века часть может преобразовать целое радикальным и неожиданным образом.
Из классической термодинамики известно, что изолированные термодинамические системы в соответствии со вторым началом термодинамики для необратимых процессов энтропия системы S возрастает до тех пор, пока не достигнет своего максимального значения в состоянии термодинамического равновесия. Возрастание энтропии сопровождается потерей информации о системе.
Со временем открытия второго закона термодинамики встал вопрос о том, как можно согласовать возрастание со временем энтропии в замкнутых системах с процессами самоорганизации в живой и не живой природе. Долгое время казалось, что существует противоречие между выводом второго закона термодинамики и выводами эволюционной теории Дарвина, согласно которой в живой природе благодаря принципу отбора непрерывно происходит процесс самоорганизации.
Противоречие между вторым началом термодинамики и примерами высокоорганизованного окружающего нас мира было разрешено с появлением более пятидесяти лет назад и последующим естественным развитием нелинейной неравновесной термодинамики. Ее еще называют термодинамикой открытых систем. Большой вклад в становление этой новой науки внесли И.Р.Пригожин, П.Гленсдорф, Г.Хакен. Бельгийский физик русского происхождения Илья Романович Пригожин за работы в этой области в 1977 году был удостоен Нобелевской премии.
Реклама

Как итог развития нелинейной неравновесной термодинамики появилась совершенно новая научная дисциплина синергетика - наука о самоорганизации и устойчивости структур различных сложных неравновесных систем: физических, химических, биологических и социальных.
В настоящей работе исследуется самоорганизация различных систем аналитическими и численными методами.
ГЛАВА 1
ОСНОВНЫЕ ПОНЯТИЯ И ИСХОДНЫЕ ПОЛОЖЕНИЯ
ТЕРМОДИНАМИКИ.
1.1.
ЗАКРЫТЫЕ И ОТКРЫТЫЕ ТЕРМОДИНАМИЧЕСКИЕ
СИСТЕМЫ.
Всякий материальный объект, всякое тело , состоящее из большого числа частиц, называется макроскопической системой .
Размеры макроскопических систем значительно больше размеров атомов и молекул. Все макроскопические признаки , характеризующие такую систему и ее отношение к окружающим телам , называются макроскопическими параметрами .
К их числу относятся такие , например , как плотность , объем , упругость , концентрация , поляризованность , намогниченность и т.д. Макроскопические параметры разделяются на внешние и внутренние .
Величины , определяемые положением не входящих в нашу систему внешних тел , называются внешними параметрами ,
например напряженность силового поля ( так как зависят от положения источников поля - зарядов и токов , не входящих в нашу систему ) , объем системы ( так как определяется расположением внешних тел ) и т.д. Следовательно внешние поараметры являются функциями координат внешних тел. Величины, определяемые совокупным движением и распределением в пространстве входящих в систему частиц , называются внутренними параметрами ,
например энергия , давление , плотность , намогниченность , поляризованность и т.д. ( так как их значения зависят от движения и положения частиц системы и входящих в них зарядов ).
Совокупность независимых макроскопических параметров определяет состояние системы , т.е. форму ее бытия . Величины не зивисящие от предыстории системы и полностью определяемые ее состоянием в данный момент ( т.е. совокупностью независимых параметров ), называются функциями состояния.
Состояние называется стационарным ,
если параметры системы с течением времени не изменяются.
Реклама

Если , кроме того , в системе не только все параметры постоянны во времени , но и нет никаких стационарных потоков за счет действия каких-либо внешних источников , то такое состояние системы называется равновесным
( состояние термодинамического равновесия ). Термодинамическими системами обычно называют не всякие , а только те макроскопические системы , которые находятся в термодинамическом равновесии. Аналогично , термодинамическими параметрами называются те параметры , которые характеризуют систему в термодинамическом равновесии.
Внутренние параметры системы разделяются на интенсивные и экстенсивные . Параметры не зависящие от массы и числа частиц в системе , называются интенсивными
( давление , температура и др.) . Параметры пропорциональные массе или числу частиц в системе , называются аддитивными
или экстенсивными
( энергия , энтропия и др. ) . Экстенсивные параметры характеризуют систему как целое , в то время как интенсивные могут принимать определенные значения в каждой точке системы .
По способу передачи энергии , вещества и информации между рассматриваемой системы и окружающей средой термодинамические системы классифицируются :
1. Замкнутая ( изолированная ) система
- это система в которой нет обмена с внешними телами ни энергией , ни веществом ( в том числе и излучением ) , ни информацией .
2. Закрытая система
- система в которой есть обмен только с энергией .
3. Адиабатно изолированная система -
это система в которой есть обмен энергией только в форме теплоты .
4. Открытая система
- это система , которая обменивается и энергией , и веществом , и информацией .
1.2.
НУЛЕВОЕ НАЧАЛО ТЕРМОДИНАМИКИ .
Нулевое начало термодинамики сформулированное всего около 50 лет назад , по существу представляет собой полученное «задним числом» логическое оправдание для введения понятия температуры физических тел . Температура - одно из самых глубоких понятий термодинамики . Температура играет столь же важную роль в термодинамике , как , например процессы. Впервые центральное место в физике занял совершенно абстрактное понятие ; оно пришло на смену введенному еще во времена Ньютона ( 17 век) понятию силы - на первый взгляд более конкретному и «осязаемому» и к тому же успешно « математезированному» Ньютоном.
Первое начало термодинамики устанавливает внутренняя энергия системы является однозначная функция ее состояния и изменяется только под влиянием внешних воздействий.
В термодинамике рассматриваются два типа внешних взаимодействий: воздействие , связанное с изменением внешних параметров системы ( система совершает работу W ), и воздействие не связанные с изменением внешних параметров и обусловленные изменением внутренних параметров или температуры ( системе сообщается некоторое количество теплоты Q ).
Поэтому , согласно первому началу , изменение внутренней энергии U2
-U1
системы при ее переходе под влиянием этих воздействий из первого состояния во второе равно алгебраической сумме Q и W , что для конечного процесса запишется в виде уравнения
U2
- U1
= Q - W или Q = U2
- U1
+ W (1.1)
Первое начало формируется как постулат и является обобщением большого количества опытных данных .
Для элементарного процесса уравнение первого начала
такого :
dQ = dU + dW (1.2)
dQ и dW не являются полным дифференциалом, так как зависят от пути следования.
Зависимость Q и W от пути видна на простейшем примере расширение газа. Работа совершенная системой при переходе ее из состояния 1 в 2 ( рис. 1) по пути а
изображается площадью, ограниченной контуром А1а2ВА
:
Wа
= p(V,T) dV ;
а работа при переходе по пути в
- площадью ограниченную контуром А1в2ВА:
Wb
= p(V,T) dV.

Рис. 1
Поскольку давление зависит не только от объема, но и от температуры, то при различных изменениях температуры на пути а и в при переходе одного и того же начального состояния (p1
,V1
) в одно и тоже конечное (p2
,V2
) работа получается разной. Отсюда видно , что при замкнутом процессе (цикле) 1а2в1 система совершает работу не равную нулю. На этом основана работа всех тепловых двигателей.
Из первого начала термодинамики следует, что работа может совершаться или за счет изменения внутренней энергии , или за счет сообщения системе количества теплоты . В случае если процесс круговой , начальное и конечное состояние совпадают U2
- U1
= 0 и W = Q , то есть работа при круговом процессе может совершаться только за счет получения системой теплоты от внешних тел .
Первое начало можно сформулировать в нескольких видах :
1. Невозможно возникновение и уничтожение энергии .
2. Любая форма движения способна и должна превращаться в любую другую форму движения .
3. Внутренняя энергия является однозначной формой состояния .
4. Вечный двигатель первого рода невозможен .
5. Бесконечно малое изменение внутренней энергии является полным дифференциалом.
6. Сумма количества теплоты и работы не зависит от пути процесса.
Первый закон термодинамики , постулируя закон сохранения
энергии для термодинамической системы. не указывает направление происходящих в природе процессов. Направление термодинамических процессов устанавливает второе начало термодинамики.
1.4.
ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ.
Второе начало термодинамики устанавливает наличие в природе фундаментальной асимметрии , т.е. однонаправленности всех происходящих в ней самопроизвольных процессов .
Второй основной постулат термодинамики связан так же с другими свойствами термодинамического равновесия как особого вида теплового движения. Опыт показывает , что если две равновесные системы А и В привести в тепловой контакт , то независимо от различия или равенства у них внешних параметров они или остаются по прежнему в состоянии термодинамического равновесия , или равновесие у них нарушается и спустя некоторое время в процессе теплообмена ( обмена энергией ) обе системы приходят в другое равновесное состояние. Кроме того , если имеются три равновесные системы А,В и С и если системы А и В поразнь находятся в равновесии с системой С, то системы А и В находятся в термодинамическом равновесии и между собой (свойства транзитивности термодинамического равновесия ).
Пусть имеются две системы . Для того , чтобы убедится в том , что они находятся в состоянии термодинамического равновесия надо измерить независимо все внутренние параметры этих систем и убедиться в том , что они постоянны во времени. Эта задача черезвычайно трудная .
Оказывается однако , что имеется такая физическая величина , которая позволяет сравнить термодинамические состояния двух систем и двух частей одной системы без подробного исследования и внутренних параметров. Эта величина , выражающая состояние внутреннего движения равновесной системы , имеющая одно и то же значение у всех частей сложной равновесной системы независимо от числа частиц в них и определяемое внешними параметрами и энергией называется температурой
.
Температура является интенсивным параметром и служит мерой интенсивности теплового движения молекул.
Изложенное положение о существовании температуры как особой функции состояния равновесной системы представляет второй постулат термодинамики.
Иначе говоря , состояние термодинамического равновесия определяется совокупностью внешних параметров и температуры.
Р.Фаулер и Э.Гуггенгейм назвали его нулевым началом , так как оно подобно первому и второму началу определяющим существование некоторых функций состояния , устанавливает существование температуры у равновесных систем. Об этом упоминалось выше.
Итак , все внутренние параметры равновесной системы являются функциями внешних параметров и температур .
(Второй постулат термодинамики).
Выражая температуру через внешние параметры и энергию , второй постулат можно сформулировать в таком виде : при термодинамическом равновесии все внутренние параметры являются функциями внешних параметров и энергии.
Второй постулат позволяет определить изменение температуры тела по изменению какого либо его параметра , на чем основано устройство различных термометров.
1.4.1.
ОБРАТИМЫЕ И НЕОБРАТИМЫЕ ПРОЦЕССЫ.
Процесс перехода системы из состояния 1 в 2 называется обратимым
, если возвращением этой системы в исходное состояние из 2 в 1 можно осуществить без каких бы то ни было изменений окружающих внешних телах.
Процесс же перехода системы из состояния 1 в 2 называется необратимым
, если обратный переход системы из 2 в 1 нельзя осуществить без изменения в окружающих телах .
Мерой необратимости процесса в замкнутой системе является изменением новой функции состояния - энтропии , существование которой у равновесной системы устанавливает первое положение второго начала о невозможности вечного двигателя второго рода . Однозначность этой функции состояния приводит к тому , что всякий необратимый процесс является неравновесным.
Из второго начала следует , что S является однозначной функцией состояния. Это означает , что dQ/T для любого кругового равновесного процесса равен нулю. Если бы это не выполнялось , т.е. если бы энтропия была неоднозначной функцией состояния то , можно было бы осуществить вечный двигатель второго рода.
Положение о существовании у всякой термодинамической системы новой однозначной функцией состояния энтропии S , которая при адиабатных равновесных процессах не изменяется и состовляет содержание второго начала термодинамики для равновесных процессов.
Математически второе начало термодинамики для равновесных процессов записывается уравнением:
dQ/T = dS или dQ = TdS (1.3)
Интегральным уравнением второго начала для равновесных круговых процессов является равенство Клаузиуса :
dQ/T = 0 (1.4)
Для неравновесного кругового процесса неравенство Клаузиуса имеет следующий вид :
dQ/T < 0 (1.5)
Теперь можно записать основное уравнение термодинамики для простейшей системы находящейся под всесторонним давлением :
TdS = dU + pdV (1.6)
Обсудим вопрос о физическом смысле энтропии.
1.4.2. ЭНТРОПИЯ.
Второй закон термодинамики постулирует существование функции состояния , называемой «энтропией» ( что означает от греческого «эволюция» ) и обладающей следующими свойствами :
а) Энтропия системы является экстенсивным свойством . Если система состоит из нескольких частей , то полная энтропия системы равна сумме энтропии каждой части .
в) Изменение энтропии d S состоит из двух частей . Обозначим через dе
S поток энтропии, обусловленный взаимодействием с окружающей средой , а через di
S - часть энтропии , обусловленную изменениями внутри системы , имеем
d S = de
S + di
S (1.7)
Приращение энтропии di
S обусловленное изменением внутри системы , никогда не имеет отрицательное значение . Величина di
S = 0 , только тогда , когда система претерпевает обратимые изменения , но она всегда положительна , если в системе идут такие же необратимые процессы.
Таким образом
di
S = 0 (1.8)
( обратимые процессы );
di
S > 0 (1.9)
( необратимые процессы );
Для изолированной системы поток энтропии равен нулю и выражения (1.8) и (1.9) сводятся к следующему виду :
d S = di
S > 0 (1.10)
( изолированная система ).
Для изолированной системы это соотношение равноценно классической формулировке , что энтропия никогда не может уменьшаться , так что в этом случае свойства энтропийной функции дают критерий , позволяющий обнаружить наличие необратимых процессов . Подобные критерии существуют и для некоторых других частных случаев .
Предположим , что система , которую мы будем обозначать символом 1
, находится внутри системы 2
большего размера и что общая система , состоящая системы 1
и 2
, является изолированной.
Классическая формулировка второго закона термодинамики тогда имеет вид :
d S = d S1
+ d S2
³ 0 (1.11)
Прилагая уравнения (1.8) и (1.9) в отдельности каждой части этого выражения , постулирует , что di
S1
³ 0 , di
S2
³ 0
Ситуация при которой di
S1
> 0 и di
S2
< 0 , а d( S1
+ S2
)>0 , физически неосуществима . Поэтому можно утверждать , что уменьшение энтропии в отдельной части системы , компенсируемое достаточным возрастанием энтропии в другой части системы , является запрещенным процессом . Из такой формулировки вытекает , что в любом макроскопическом участке системы приращение энтропии , обусловленное течением необратимых процессов , является положительным. Под понятием « макроскопический участок » системы подразумевается любой участок системы , в котором содержится достаточное большое число молекул , чтобы можно было принебреч микроскопическими флуктуакциями. Взаимодействие необратимых процессов возможно лишь тогда, когда эти процессы происходят в тех же самых участках системы .
Такую формулировку второго закона можно было бы назвать « локальной » формулировка в противоположность « глобальной » формулировка классической термодинамики . Значение подобной новой формулировке состоит в том ,что на ее основе возможен гораздо более глубокий анализ необратимых процессов .
1.5
ТРЕТЬЕ НАЧАЛО ТЕРМОДИНАМИКИ.
Открытие третьего начала термодинамики связано с нахождением химического средства - величины , характеризующих способность различных веществ химически реагировать друг с другом . Эта величина определяется работой W химических сил при реакции . Первое и второе начало термодинамики позволяют вычислить химическое средство W только с точностью до некоторой неопределенной функции . Чтобы определить эту функцию нужны в дополнении к обоим началам термодинамики новые опытные данные о свойствах тел . Поэтому Нернстоном были предприняты широкие экспериментальные исследования поведение веществ при низкой температуре .
В результате этих исследований и было сформулировано третье начало термодинамики : по мере приближения температуры к 0 К энтропия всякой равновесной системы при изотермических процессах перестает зависить от каких-либо термодинамических параметров состояния и в пределе ( Т= 0 К) принимает одну и туже для всех систем универсальную постоянную величину , которую можно принять равной нулю .
Общность этого утверждения состоит в том , что , во-первых , оно относится к любой равновесной системе и , во-вторых , что при Т стремящемуся к 0 К энтропия не зависит от значения любого параметра системы. Таким образом по третьему началу,
lin [ S (T,X2
) - S (T,X1
) ] = 0 (1.12)
или
lim [ dS/dX ]T
= 0 при Т ® 0 (1.13)
где Х - любой термодинамический параметр (аi
или Аi
).
Предельно значение энтропии , поскольку оно одно и тоже для всех систем , не имеет никакого физического смысла и поэтому полагается равным нулю (постулат Планка). Как показывает статическое рассмотрение этого вопроса , энтропия по своему существу определена с точностью до некоторой постоянной (подобно, например, электростатическому потенциалу системы зарядов в какой либо точке поля). Таким образом , нет смысла вводить некую «абсолютную энтропию», как это делал Планк и некоторые другие ученые.
ГЛАВА 2
ИЗОПРОЦЕССЫ В ГАЗАХ
2.1. Уравнение состояние идеального газа
Состояния данной массы газа характеризуется тремя макроскопическими параметрами: давлением, объемом, температурой. В данной главе рассмотрим между ними связь, а затем посмотрим, для чего эта связь нужна.
Уравнение состояния идеального газа
– называется такое уравнение, которое связывает три макроскопических параметра давление P
, объем V
и температуру T
, для достаточно разряженного газа.
Выведем уравнение состояния идеального газа. Для этого подставим в уравнение:
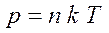 (1
) (1
)
выражение для концентрации молекул газа  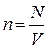 , концентрацию газа можно записать так: , концентрацию газа можно записать так:
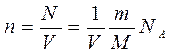 (2
) (2
)
где 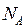 -постоянная Авогадро, m
– масса газа, M
– его молярная масса. -постоянная Авогадро, m
– масса газа, M
– его молярная масса.
После подстановки (2
) в (1
) будем иметь

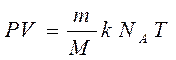 (3
) (3
)
где k
– постоянная Больцмана. Произведение постоянной Больцмана k и постоянной Авогадро 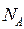 называется универсальной (молярной) газовой постоянной
и обозначается буквой R. называется универсальной (молярной) газовой постоянной
и обозначается буквой R.
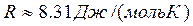
Подставим универсальную газовую постоянную в уравнение (3
), получим уравнение состояния для произвольной массы идеального газа:
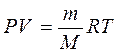 (4
) (4
)
Единственная величина в этом уравнении (4
), зависящая от рода газа, это его молярная масса.
Уравнение (4
) называется уравнение состояния идеального газа
или уравнение Менделеева – Клапейрона.
Из уравнения состояния вытекает связь между давлением, объемом и температурой идеального газа, который может находиться в двух любых состояниях.
Если индекс 1
обозначить параметры, относящиеся к первому состоянию, а индекс 2
- параметры, относящиеся ко второму состоянию, то согласно уравнению (4
) для газа данной массы:
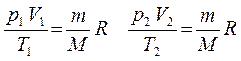
Правые части этих уравнений одинаковы, следовательно, должны быть равны и их левые части:
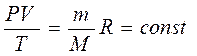 (5
) (5
)
Уравнение состояние в форме (5
) называется уравнением Клапейрона и представляет собой одну из форм записи уравнения состояния.
Таким образом, для данной массы газа, как бы ни менялись его давление, объем и температура, произведение давления на объем, деленное на абсолютную температуру, есть величина постоянная.
2.2.
Изотермический процесс
Процесс изменения состояния термодинамической системы макроскопических тел при постоянной температуре называется изотермическим
.
Для поддержания температуры газа постоянной необходимо, чтобы он мог обмениваться теплотой с большой системой – термостатом. Термостатом может служить атмосферный воздух, если температура его заметно не меняется на протяжении всего процесса.
Из уравнения состояния идеального газа (4
) следует, что при постоянной температуре Т
и неизменных значениях массы газа m
и его молярной массы M
произведение давления Р
газа на его объем V
должно оставаться постоянным:
PV
=
const
при T
=
const
Для газа данной массы произведение давления газа на его объем постоянно, если температура газа не меняется.
Изотермический процесс можно осуществить, например, путем изменения объема газа при постоянной температуре.
Этот закон экспериментально был открыт английским ученым Р. Бойлем (1627-1691) и несколько позже французским ученым Э. Мариоттом (1620-1684). Поэтому он носит название закона Бойля – Мариотта.
Закон Бойля – Мариотта справедлив для любых газов, а также и для их смесей (например, для воздуха). Лишь при давлениях, в несколько сотен раз больших атмосферного, отклонения от этого закона становятся существенными.
Зависимость давления газа от объема при постоянной температуре графически изображается кривой, которая называется изотермой
. Изотерма газа изображается обратно пропорциональную зависимость между давление и объемом.
Кривая такого рода называется гипербола (рис.1
).
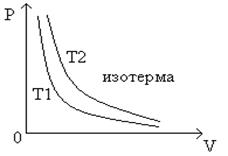
Рис.1
График зависимости между давлением и объемом газа при постоянной температуре
Разным постоянным температурам соответствуют различные изотермы. При повышении температуры давление согласно уравнению состояния (4
) увеличивается, если V
=
const
. Поэтому изотерма, соответствующая более высокой температуре 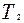 , лежит выше изотермы, соответствующей более низкой температуре , лежит выше изотермы, соответствующей более низкой температуре 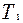 . .
В системах координат p
,
T
(рис.2
) и V
,
T
(рис.3
) изотермический процесс изображается прямой, параллельной соответственно оси p
или V
. Эти прямые также изотермы. Третий параметр (V
или p
) не сохраняет вдоль них постоянного значения.
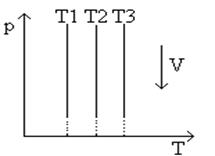
Рис.2
График изотермического процесса в координатах p,T
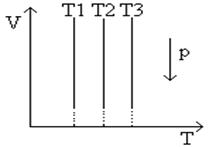
Рис.3
График изотермического процесса в координатах V,T
Изотермический процесс протекает медленно, так как он обусловлен теплообменом с окружающей средой.
2.3.
Изобарический процесс
Процесс изменения состояния термодинамической системы при постоянном давлении называется изобарным
. Изобарный процесс протекает при неизменном давлении p
и условии m
=
const
и M
=
const
.
Согласно уравнению (4
) в любом состоянии газа с неизменным давлением отношение объема газа к его температуре остается постоянным:
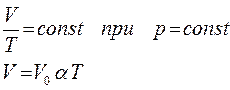
где V
– объем газа при абсолютной температуре T
, V
0
– объем газа при температуре 00
С
; коэффициент α, равный 1/273 К-1
, называется температурным коэффициентом объемного расширения газов.
Для газа данной массы отношение объема к температуре постоянно, если давление газа не меняется.
Этот закон был установлен экспериментально в 1802г. французским ученым Ж. Гей-Люссаком (1778 – 1850) и носит название закон Гей-Люссака
.
Формулу закона Гей-Люссака можно переписать в виде:
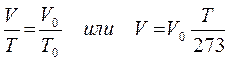
Таким образом, при неизменной массе газа и постоянном давлении его объем с повышением температуры на 1 градус увеличивается на 1/273 часть того объема, который газ занимает при 273К (00
С).
Графически такой процесс изображается прямой с помощью координатных осей V
,
T
продолжение которой проходит через начало координат. Называют эту прямую изобарой
(рис.4
).
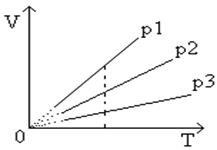
Рис.4
Графическая зависимость изобарического процесса
Угол ее наклона α
к оси температур зависит от давления газа: чем больше давление, тем меньше угол наклона (p
3
>
p
2
>
p
1
).
Различным давлениям соответствуют разные изобары. С ростом давления объем газа при постоянной температуре согласно закону Бойле - Мариотта уменьшается. Поэтому изобара, соответствующая более высокому давлению p
2
, лежит ниже изобары, соответствующей более низкому давлению p
1
.
Следовательно, при одной и той же температуре газ будет занимать тем больший объем, чем меньше его давление. На диаграммах с координатными осями p
,
V
или p
,
T
изобары имеют вид прямых, параллельных оси Т
или, соответственно оси V
(рис.5, рис.6
).
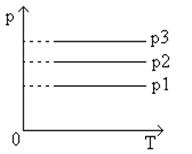
Рис.5
График изобарического процесса в координатах p,T
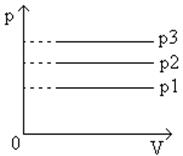
Рис.6
График изобарического процесса в координатах p,V
Изобарным можно считать расширение газа при нагревании его в цилиндре с подвижным поршнем. Постоянство давления в цилиндре обеспечивается атмосферным давлением на внешнюю поверхность поршня.
2.4 Изохорический процесс
Процесс изменения состояния термодинамической системы при постоянном объеме называют изохорным
. Изохорный процесс, протекающий при неизменном объеме V
и условии m
=
const
и M
=
const
.
При этих условиях из уравнения состояния идеального газа (4
) вытекает, что в любом состоянии газа с неизменным объемом отношение давления газа к его температуре остается постоянным:
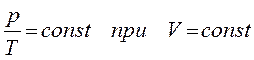
Для газа данной массы отношение давления к температуре постоянно, если объем не меняется.
Этот газовый закон был установлен в 1787г. французским физиком Ж. Шарлем (1746 – 1823) и носит название закон Шарля
.
График уравнения изохорного процесса называется изохорой. Изохора, изображенная в прямоугольной системе координат по оси ординат которой отсчитывается давление газа, а по оси абсцисс – его абсолютная температура, является прямой, проходящей через начало координат (рис.7
).
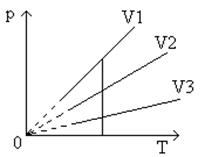
Рис.7
Графическая зависимость изохорического процесса
Угол наклона α
изохоры к оси температур тем больше, чем меньше объем газа (V
3
>
V
2
>
V
1
).
Разные объемам соответствуют разные изохоры. С ростом объема газа при постоянной температуре давление его согласно закону Бойля – Мариотта падает. Поэтому изохора, соответствующая большому объему V2
, лежит ниже изохоры, соответствующей объему V1
.
В системах координат p, V и V, T изохора имеет вид прямой, параллельной оси p или, соответственно, Т (рис.8, рис.9
).
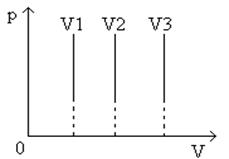
Рис.8
График изохорического процесса в координатах p, V
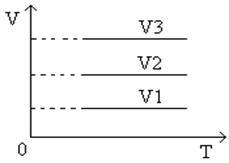
Рис.9
График изохорического процесса в координатах V, T
Увеличение давления газа в любой емкости или в электрической лампочке при нагревании является изохорным процессом. Изохорный процесс используется в газовых термометрах постоянного объема. Также изохорный процесс можно осуществить при нагревании воздуха при постоянном объеме.
2.5.Адиабатический процесс
Кроме изобарного, изохорного и изотермического процессов, в термодинамике часто рассматриваются адиабатные процессы.
Адиабатным процессом называется процесс, происходящий в термодинамической системе при отсутствии теплообмена с окружающими телами, то есть при условии Q
= 0
.
Отсутствие теплообмена с окружающей средой может быть обеспечено хорошей теплоизоляцией газа. Быстрые процессы расширения или сжатия газа могут быть близкими к адиабатическому и при отсутствии теплоизоляции, если время, за которое происходит изменение объема газа, значительно меньше времени, необходимого для установления теплового равновесия газа с окружающими телами.
Примерами адиабатных процессов могут служить процессы сжатия воздуха в цилиндре воздушного огнива, в цилиндре двигателя внутреннего сгорания. В соответствии с первым законом термодинамики, при адиабатном сжатии изменение внутренней энергии газа ΔU равно работе внешних сил А:
Δ
U
= А
Так как работа внешних сил при сжатии положительна, внутренняя энергия газа при адиабатном сжатии увеличивается, его температура повышается.
При адиабатном расширении газ совершает работу А'
за счет уменьшения своей внутренней энергии:
Δ
U
= - А'
Поэтому температура газа при адиабатном расширении понижается. Это можно обнаружить в следующем опыте. Если в бутылку, содержащую насыщенный водяной пар, накачивать с помощью насоса воздух, то пробка вылетает. Работа А' по выталкиванию пробки совершается воздухом за счет уменьшения его внутренней энергии, так как расширение воздуха происходит за очень короткое время и теплообмен с окружающей средой не успевает произойти. Образование капель тумана доказывает, что при адиабатном расширении воздуха его температура понизилась и опустилась ниже точки росы.
Поскольку при адиабатном сжатии температура газа повышается, то давление газа с уменьшением объема растет быстрее, чем при изотермическом процессе. Понижение температуры газа при адиабатном расширении приводит к тому, что давление газа убывает быстрее, чем при изотермическом расширении.
График адиабатного процесса в координатных осях p, V представлен на (рис.10
).
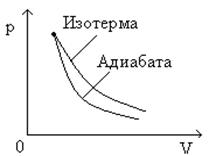
Рис.10
График адиабатного процесса в координатных p, V
На этом же рисунке для сравнения приведен график изотермического процесса.
Адиабатное охлаждение газов при их расширении используется в машинах для сжижения газов. Охлаждение газа при адиабатном расширении происходит в грандиозных масштабах в атмосфере Земли. Нагретый воздух поднимается вверх и расширяется, так как атмосферное давление падает с увеличением высоты. Это расширение сопровождается значительным охлаждением. В результате водяные пары конденсируются и образуют облака.

ЛИТЕРАТУРА
:
1. Базаров И.П. Термодинамика. - М.: Высшая школа, 1991 г.
2. Гленсдорф П. , Пригожин И. Термодинамическая теория структуры , устойчивости и флуктуаций. - М.: Мир, 1973 г.
3. Карери Д. Порядок и беспорядок в структуре материи. - М.: Мир, 1995 г.
4. Курдюшов С.П. , Малинецкий Г.Г. Синергетика - теория самоорганизации. Идеи , методы перспективы. - М.: Знание, 1983 г.
5. Николис Г. , Пригожин И. Самоорганизация в неравновесных системах. - М.: Мир, 1979 г.
6. Николис Г. , Пригожин И. Познание сложного. - М.: Мир, 1990 г.
7. Перовский И.Г. Лекции по теории дифференциальных уравнений. - М.: МГУ, 1980 г.
8. Попов Д.Е. Междисциплинарные связи и синергетика. - КГПУ, 1996 г.
9. Пригожин И. Введение в термодинамику необратимых процессов. - М.: Иностранная литература , 1960 г.
10. Пригожин И. От существующего к возникающему. - М.: Наука, 1985 г.
11. Синергетика , сборник статей. - М.: Мир, 1984 г.
12. Хакен Г. Синергетика . - М.: Мир , 1980 г.
13. Хакен Г. Синергетика . Иерархия неустойчивостей в самоорганизующихся системах и устройствах . - М.: Мир , 1985 г.
14. Шелепин Л.А. В дали от равновесия. - М.: Знание, 1987 г.
15. Эйген М. , Шустер П. Гиперцикл . Принципы самоорганизации макромолекул . - М.: Мир , 1982 г.
16. Эткинс П. Порядок и беспорядок в природе. - М.: Мир , 1987 г

|