| СОДЕРЖАНИЕ
1. Введение .............................................................................................................4
2.1. Задание на проектирование............................................................................4
2.2. Структурный анализ рычажного механизма.................................................5
2.3. Кинематический анализ рычажного механизма...........................................6
2.3.1. Построение положений звеньев..................................................................6
2.3.2. Определение скоростей звеньев механизма..............................................7
2 3.3. Определение ускорений точек звеньев механизма...................................8
2.4. Кинетостатический анализ механизма.........................................................11
2.4.1. Определение сил, действующих на звенья механизма............................11
2.4.2. Определение реакций в кинематических парах......................................12
2.4.3. Силовой расчет входного звена механизма..............................................14
2.4.4. Определение уравновешивающей силы методом Жуковского.............14
Библиографический список...................................................................................16
1. Введение
Кривошип ОА, вращаясь вокруг оси О, действует на коромысло АВ и через коромысло АВ передает движение кривошипу СВ, связанному с кривошипом CD, которые совершают вращательное движение относительно оси C. Кривошип CD через коромысло DE передает движение коромыслу FЕ. Механизм состоит из 5 подвижных звеньев, 7 вращательных пар 5 класса и обладает полной определенностью движения всех звеньев.
2.1. Задание на проектирование
Кинематическая схема рычажного механизма показана на рис. 2.1. Диаграмма технологической силы, действующей на кулису F
Е
, изображена на
рис. 2.2. Размеры и массы звеньев механизма указаны в табл. 2.1.
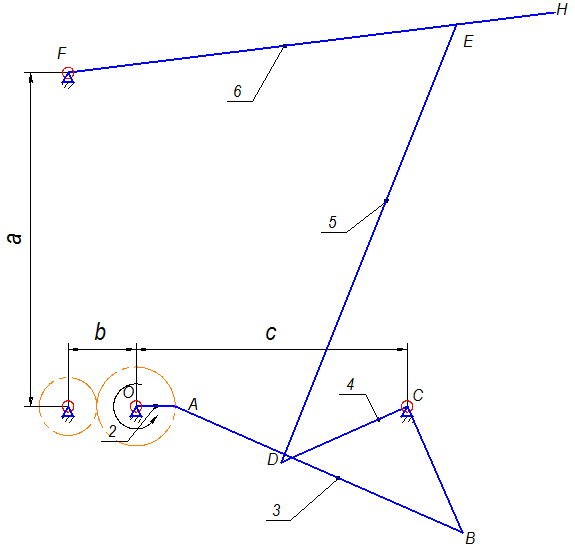
Рис. 2.1. Кинематическая схема рычажного механизма
Таблица 2.1
Исходные данные для проекта
| Наименование параметра
|
Обозначение и величина
|
Длина кривошипа ОА
, м
|

|
Длина шатуна АВ
, м
|
LAB
= 0,8
|
Длина кривошипа СВ
, м
|
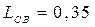
|
Длина кривошипа С
D
, м
|
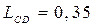
|
| Длина кулисы D
Е
, м
|
LD
Е
= 0,35+0,85=1,2
|
| Длина кулисы FH
, м
|
LFH
= 1,25
Реклама

|
| FH
/
F
Е
|
0,8
|
| Масса кривошипа ОА
, кг
|
m
1
= 20
|
Масса шатуна АВ
, кг
|
m
2
= 160
|
Масса кривошипа BCD
, кг
|
m
3
=140
|
| Масса кулисы ED
, кг
|
m
4
= 240
|
Масса кулисы FH
,
кг
|
m
5
= 250
|
| Моменты инерции звеньев IS
i
относительно их центров тяжести, кг·м2
.
|
IS
1
=
0,02;
IS
2
=
10,2;
IS
3
=
6,8;
IS
4
=
34,6;
IS
4
=
39,1
|
| Частота вращения ОА
, рад/с
|
ω
OA
= 10
|
| Коэффициент неравномерности хода машины
|
d = 0,08
|
| Числа зубьев зубчатых колес
|
z1
=
16;
z
2
=
25
|
| Модуль зубчатых колес, мм
|
m =
16
|
| Центры тяжести звеньев, обозначенные буквой S
,
расположены на середине звеньев
|
| Схема и параметры кулачкового механизма представлены в соответствующем разделе проекта
|
| Технологическое усилие, действующее на ползун Н
при его движении вверх, равно Q
=
6000 Н. (см. рис. 2.)
|
2.2. Структурный анализ рычажного механизма
Кинематическая схема рычажного механизма показана на рис. 2.1.
Механизм плоский рычажный.
Для этого механизма: n
= 5; p
5
= 7; p
4
= 0.
Степень подвижности плоского механизма определяется по формуле
П. Л. Чебышева:
W
= 3 n
– 2 p
5
─ p
4
= 3∙5 ─ 2∙7 – 0 = 1,
где n
─ число подвижных звеньев;
p
5
─ число пар пятого класса;
p
4
─ число пар четвёртого класса.
Согласно полученному результату для определенности движения всех звеньев механизма необходимо иметь одно входное звено.
Разложение механизма на группы Ассура показано на рис. 2.2
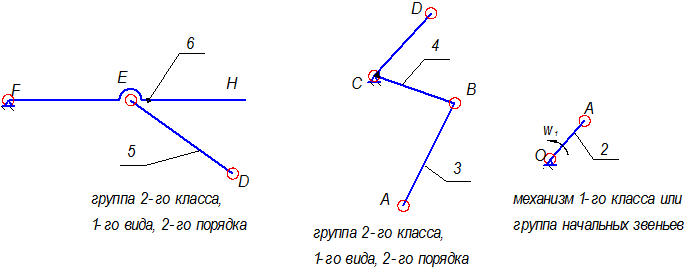
Рис.2.2. Строение механизма
Определим степень подвижности каждой группы в отдельности:
а) группа Ассура 2-го класса, 2-го вида:
W
= 3n
– 2p
5
– p
4
= 3∙2 – 2∙3 – 0 = 0,
б) группа Ассура 2-го класса, 1-го вида:
W
= 3n
– 2p
5
– p
4
= 3∙2 – 2∙3 – 0 = 0,
в) механизм 1-го класса:
W
= 3∙n
– 2∙p
5
– p
4
= 3∙1 – 2∙1 – 0 = 1.
Вывод: рассматриваемый механизм является механизмом 2-го класса.
2.3.
Кинематический анализ рычажного механизма
Целью кинематического анализа является установление положений звеньев механизма, определение скоростей и ускорений его звеньев.
2.3.1. Построение положений звеньев
Задача о положениях звеньев решается на первом листе проекта графически путем построения кинематической схемы механизма в двенадцати положениях механизма. На плане механизма отобразим входное звено ОА отрезком длиной 15мм.
Масштабный коэффициент планов механизма
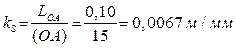 . .
2.3.2. Определение скоростей звеньев механизма
Для примера рассмотрим 2-е положение механизма
Реклама

Угловая скорость начального звена ОА
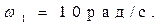
Скорость точки А
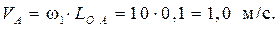
Скорости остальных точек механизма находим путем построения плана скоростей. Принимаем длину отрезка (pv
a
), изображающего скорость VA
точки А,
равной 100 мм.
Тогда масштабный коэффициент плана скоростей
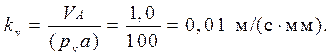
Рассматривая движение точки В
вместе с точками А
и С
(переносное движение) и относительно этих точек, получим векторные уравнения для построения скорости точки
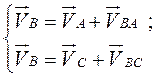
 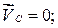 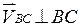 . .
Величина (модуль) скорости точки 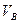
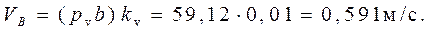
Величина (модуль) скорости точки 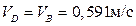
Рассматривая движение точки Е
вместе с точками D
и F
(переносное движение) и относительно этих точек, получим векторные уравнения для построения скорости точки
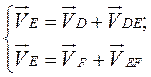
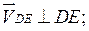 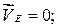 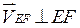 . .
Величина (модуль) скорости точки 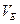
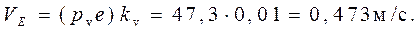
Скорость точки F
коромысла определяем с помощью теоремы подобия:
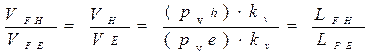 ; ;
отсюда 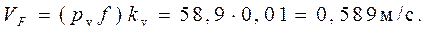 Определение скоростей центров тяжести звеньев производится с помощью теоремы подобия:
Определение скоростей центров тяжести звеньев производится с помощью теоремы подобия:
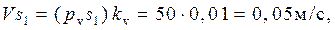
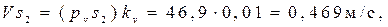
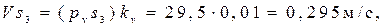
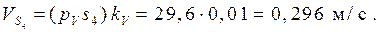
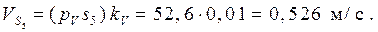
Определение угловых скоростей звеньев:
ωOA
=10 с─1
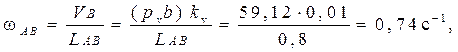
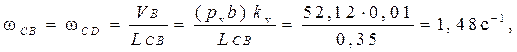
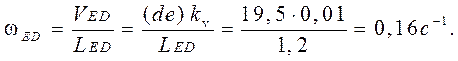
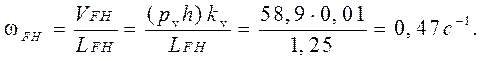
Направление угловой скорости ωАВ
определяем по относительной линейной скорости. Например, если в положении 2 к точке B
приложить вектор VBA
, то ωАВ
будет направлена против часовой стрелке. Направление угловых скоростей остальных звеньев отыскивается аналогично.
2.3.3. Определение ускорений точек звеньев механизма
Ускорение точки А
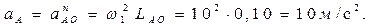
В общем случае 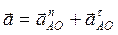 , ,
но так как 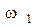 =
const, то =
const, то 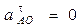 , поэтому , поэтому 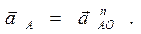
Принимаем длину отрезка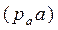 , изображающего вектор ускорения точки А
, равной 100мм, Тогда масштабный коэффициент плана ускорений , изображающего вектор ускорения точки А
, равной 100мм, Тогда масштабный коэффициент плана ускорений
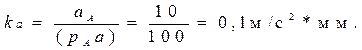
Рассматривая движение точки В
вместе с точками А
и С
(переносное движение) и относительно этих точек, получим векторные уравнения для построения ускорения точки:
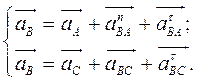
Первое уравнение: 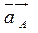 // //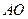 ; ;
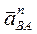 ║ АВ
; ║ АВ
; 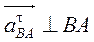 ; ;
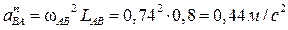
Графическое изображение вектора нормального ускорения а
n
BA
на плане ускорений равное отрезку anBA
определяется по формуле
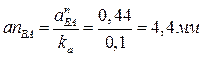
Второе уравнение: 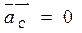 ; ;
 ║ВС
; ║ВС
; 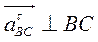 ; ;
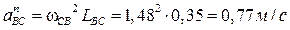 . .
Графическое изображение нормального ускорения an
B
С
определим по формуле
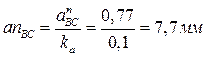
Величина (модуль) ускорения точки В
 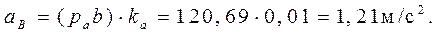
Ускорение точки D
равно ускорению точки В
и направление его перпендикулярно направление вектора ускорения точки В
.
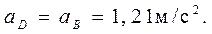
Рассматривая движение точки Е
вместе с точками D
и F
(переносное движение) и относительно этих точек, получим векторные уравнения для построения ускорения точки:

Первое уравнение: 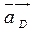 мы уже построили. мы уже построили.
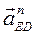 ║ ED
; ║ ED
; 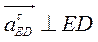 ; ;
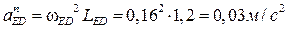
Графическое изображение вектора нормального ускорения 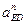 на плане ускорений равное отрезку anED
определяется по формуле
на плане ускорений равное отрезку anED
определяется по формуле
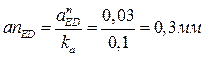
Второе уравнение: 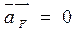 ; ;
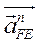 ║ ║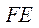 ; ; 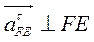 ; ;
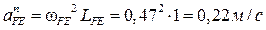 . .
Графическое изображение нормального ускорения 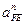 определим по формуле определим по формуле
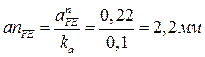
Величина (модуль) ускорения точки E
 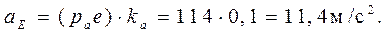
Ускорение точки Н
коромысла определяем по теореме подобия:
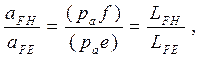
откуда 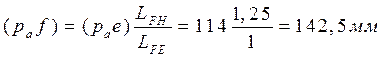 
Абсолютное ускорение точки Н
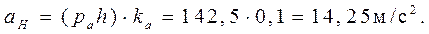
Определение ускорений центров тяжести звеньев производится с помощью теоремы подобия:
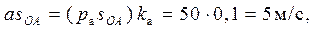
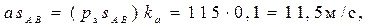
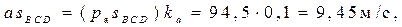
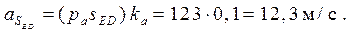
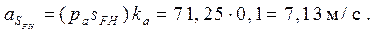
Определение угловых ускорений звеньев механизма:
Угловое ускорение звена 2 равно 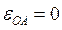 (так как (так как 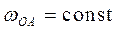 ), ),
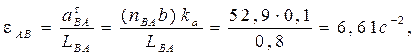
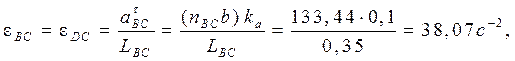
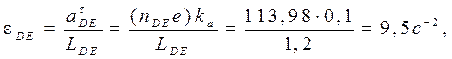
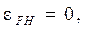
так как звено 6 совершает только поступательное движение.
Направление углового ускорения 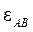 определяем по направлению вектора определяем по направлению вектора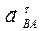 , перенесенного в точку В. Угловое ускорение , перенесенного в точку В. Угловое ускорение 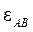 направлено по часовой стрелке. Направление угловых ускорений остальных звеньев отыскиваются аналогично. направлено по часовой стрелке. Направление угловых ускорений остальных звеньев отыскиваются аналогично.
2.4. Кинетостатический анализ механизма
Целью силового анализа является определение сил, действующих на звенья механизма, реакций в кинематических парах и уравновешивающей силы. В курсовом проекте задачи силового расчета решается в первом приближении, предполагая, что трение в кинематических парах отсутствует.
2.4.1. Определение сил, действующих на звенья механизма
Сила тяжести звеньев:
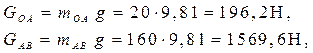
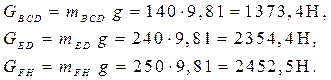
Механизм приводится в движение двигателем. Рабочее звено - 6. Сила полезного сопротивления Q
приложена в точке Н коромысла 6.
Сила сопротивления перемещению ползуна, направленная в противоположную сторону скорости V
Н
. (см. табл. 2.1):
Q
= 6000 H. (т.к. слишком большой масштаб для построения силы в 600кН)
Величины сил инерции:
ФИОА
= m
ОА
∙aS
ОА
= 20∙5 =100 H,
ФИАВ
= m
АВ
∙aS
АВ
= 160∙11,5 =1840 H,
ФИ
BCD
= mBCD
∙aSBCD
= 140∙9,45 = 1323 H,
ФИ
ED
= mED
∙aSED
= 240∙12,3 = 2952 H,
ФИ
FH
= mFH
∙aSFH
= 250∙7,13 = 1782,5 H.
Эти силы прикладываем к центрам тяжести соответствующих звеньев и направляем в сторону, противоположную вектору ускорения центра тяжести.
Моменты от сил инерции звеньев:
M
ИОА
= ISOA
∙εOA
= 0, т.к. εOA
= 0
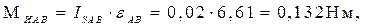
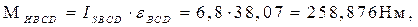
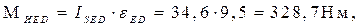
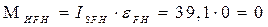
2.4.2. Определение реакций в кинематических парах
Силовой расчет механизма начинаем с группы Ассура FE
─
D
, наиболее удаленной от входного звена ОА
. На звенья этой группы действуют известные по величине и направлению силы веса G
ED
и G
FH
, силы инерции 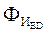 и и 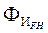 , момент , момент 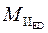 от сил инерции, технологическое усилие Q
. от сил инерции, технологическое усилие Q
.
Эту группу Ассура освобождаем от связей и вместо них прикладываем в паре D
реакцию 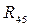 ,
а в паре F
реакцию ,
а в паре F
реакцию 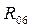 . Обе реакции не известны по величине. Реакция . Обе реакции не известны по величине. Реакция 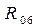 направлена перпендикулярно направляющей хх ползуна F
. Реакция направлена перпендикулярно направляющей хх ползуна F
. Реакция 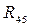 неизвестна по направлению. неизвестна по направлению.
Реакцию 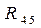 раскладываем на две взаимно перпендикулярные составляющие раскладываем на две взаимно перпендикулярные составляющие 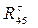 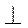 ED
и
ED
и 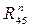 ║ED
. ║ED
.
Запишем уравнение моментов всех сил, действующих на звено 5 относительно точки E
:
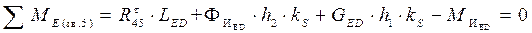 , ,
отсюда
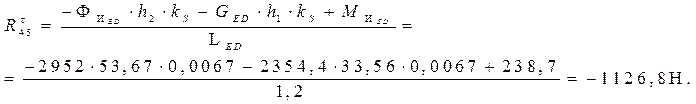
Знак минус означает, что сила 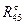 направлена в противоположную сторону, чем указана на чертеже. направлена в противоположную сторону, чем указана на чертеже.
Далее, приняв масштаб сил 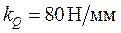 , строим план сил по векторному уравнению , строим план сил по векторному уравнению
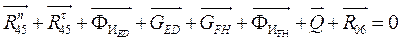 . .
Из плана сил находим величины и направления сил 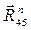 и и 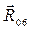 , а также полную реакцию в паре с , а также полную реакцию в паре с  ( (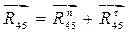 ). ). 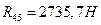 . .
Для того чтобы отыскать реакцию 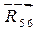 во вращающейся кинематической паре F
, приравниваем нулю сумму всех сил, действующих на звено 5: во вращающейся кинематической паре F
, приравниваем нулю сумму всех сил, действующих на звено 5:
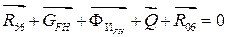 , ,
учитывая зависимость 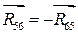 . . 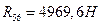 . . 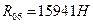 . .
Переходим к силовому расчету группы Ассура 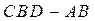 . Освобождаемся от связей и прикладываем реакцию . Освобождаемся от связей и прикладываем реакцию 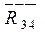 , которая неизвестна ни по величине, ни по направлению. Реакцию , которая неизвестна ни по величине, ни по направлению. Реакцию 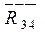 раскладываем на раскладываем на 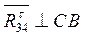 и и 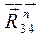 ║ C
В
. ║ C
В
.
Составим уравнение моментов всех сил, действующих на звено 4 относительно точки 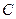 :
:
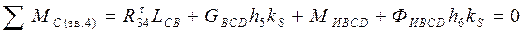 . .
Откуда 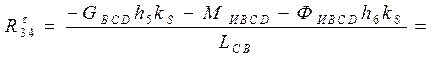
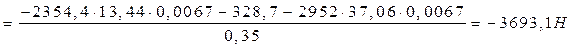
Знак минус означает, что сила 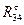 направлена в противоположную сторону, чем указана на чертеже. направлена в противоположную сторону, чем указана на чертеже.
Освобождаемся от связей и прикладываем реакцию 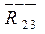 , которая неизвестна ни по величине, ни по направлению. Реакцию , которая неизвестна ни по величине, ни по направлению. Реакцию 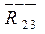 раскладываем на раскладываем на 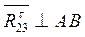 и и 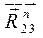 ║ АВ
. ║ АВ
.
Составим уравнение моментов всех сил, действующих на звено 3 относительно точки 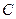 :
:
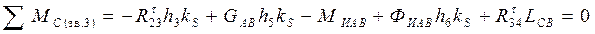 . .
Откуда 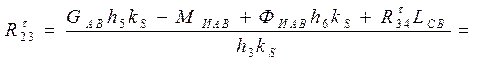
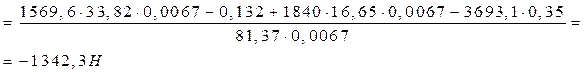
Знак минус означает, что сила 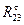 направлена в противоположную сторону, чем указана на чертеже. направлена в противоположную сторону, чем указана на чертеже.
Задавшись масштабом 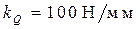 , строим план сил для всей группы Ассура , строим план сил для всей группы Ассура 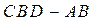 согласно векторному уравнению согласно векторному уравнению
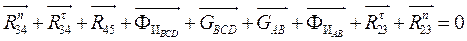
Из плана сил находим величины и направления силы 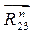 ,а также полную реакцию в кинематической паре А
и В. ,а также полную реакцию в кинематической паре А
и В.
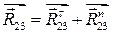 ; ; 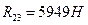
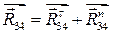 ; ; 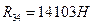
2.4.3. Силовой расчет входного звена механизма
Для определения реакции R
12
кинематической паре, образованной входным звеном со стойкой, необходимо привести в равновесие все силы, действующие на это звено с учетом уравновешивающей силы. Уравновешивающая сила является реальной внешней силой, которая представляет собой действие привода на в звено ОА.
Величину уравновешивающей силы находим из уравнения моментов относительно точки О
всех сил, действующих на звено 2:
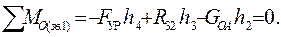
Откуда
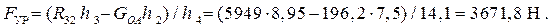
Для определения численного значения R
12
строим план сил в масштабе 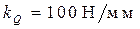 согласно векторному уравнению согласно векторному уравнению
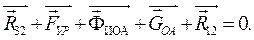
Результаты силового расчета с использованием планов сил указаны в табл. 2.4.
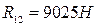
2.4.4. Определение уравновешивающей силы методом Жуковского
Для нахождения уравновешивающей силы методом Н.Е. Жуковского строится план скоростей, в соответствующие точки которого переносятся все силы (внешние и силы инерции), предварительно повернутые в одном направлении на угол 900
.
Моменты сил инерции заменяем парами сил:
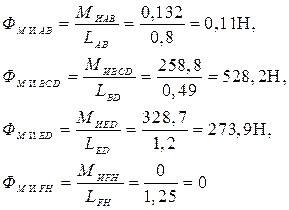
Рассматривая план скоростей как жесткий рычаг, который находится в равновесии, определим сумму моментов всех сил относительно его полюса:
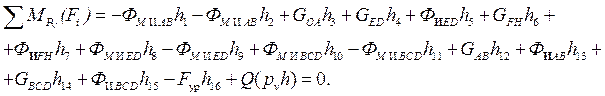
Откуда
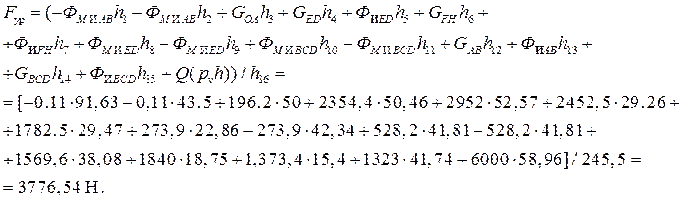
Таблица2. 4
Реакции в кинематических парах рычажного механизма для положения 2, Н.
| R
12
|
R
23,
|
R
34
|
R
45
|
R
56
|
R
06
|
F
УР
|
| 9025
|
5949
|
14103
|
2735
|
4969,6
|
15941
|
3671,8
|
По методу Н.Е.Жуковского F
УР
=3776,54
H
( погрешность от определения величины уравновешивающей силы различными методами составляет 2,8 %).
Библиографический список
1. Теория механизмов и машин: методические указания по выполнению курсового проекта /под ред. В.И. Соколовского. Свердловск.: УПИ, 1978. Ч. I. 16 с.
2. Теория механизмов и машин: методические указания по выполнению курсового проекта/ под ред. В.И.Соколовского - Свердловск.: УПИ, 1978.Ч. 2. 16 с.
3. Курсовое проектирование по теории механизмов и машин /под ред.
А.С. Кореняко . Киев.: Вища школа, 1970. 332 с.
4. Теория механизмов и механика машин /под ред. К.В. Фролова. М.: Высш. шк., 1998. 496 с.
5. Попов С.А. Курсовое проектирование по теории механизмов и машин. С.А. Попов, Т.А. Тимофеев. М.: Высш. шк., 1998. 351 с.
|