|
РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ГИДРОМЕТЕОРОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ

Тема:
«
Форма , размеры и движения Земли и их геофизические следствия. Гравитационное поле Земли. Основные характеристики, их изменения по широте, глубине и высоте над поверхностью Земли. Гравитационные аномалии. »

Выполнил: студент заочного отделения 1 курса
специальность метеорология Бондарчук А.В.
План
· Третья планета в галактике.
· Орбитальные характеристики планет.
· Внутренне строение Земли.
· Земная кора и её строение.
· Газовая оболочка Земли.
· Закон всемирного тяготения.
· Форма Земли и гравитация.
· Аномалии силы тяжести.
· Система Земля – Луна.
· Физические основы гравитационных аномалий.
· Первая в мире гравикарта.
· Список использованной литературы.
Третья планета в галактике.
Солнечная система включает девять крупных планет, которые со своими 57 спутниками обращаются вокруг массивной звезды по эллиптическим орбитам (рис. 1). По своим размерам и массе планеты можно разделить на две группы – планеты земной группы, расположенные ближе к Солнцу, – Меркурий, Венера, Земля и Марс и планеты-гиганты – Юпитер, Сатурн, Уран и Нептун, находящиеся на значительно более удаленных орбитах от центральной звезды. Последняя из известных планет Плутон своей орбитой с радиусом около 6 млрд. км очерчивает границы Солнечной системы. Плутон не относится к планетам-гигантам, его масса почти в десять раз меньше массы Земли. Аномальные характеристики этой крошечной планеты позволяют рассматривать ее как бывший спутник Нептуна.
Кроме больших планет между орбитами Марса и Юпитера вращается более 2300 малых планет – астероидов, множество более мелких тел – метеоритов и метеорной пыли, а также несколько десятков тысяч комет, двигающихся по сильно вытянутым орбитам, некоторые из которых далеко выходят за границы Солнечной системы.

Рис. 1. Солнечная система
 Все планеты и астероиды обращаются вокруг Солнца в направлении движения Земли – с запада на восток. Это так называемое прямое движение. Основные закономерности движения планет полностью определяются законами Кеплера. Рассмотрим эти законы и охарактеризуем основные элементы эллиптических орбит. Согласно первому закону, все планеты обращаются вокруг Солнца по эллиптическим орбитам, в одном из фокусов которых находится Солнце. На рис. 2 показаны элементы планетных орбит с Солнцем (С) в фокусе. Линия АП называется линией апсид, крайние точки которой афелий (А) и перигелий (П) характеризуют наибольшее и наименьшее удаление от Солнца.Расстояние планет( Р ) на орбите от Солнца (гелиоцентрическое расстояние) определяется радиусом-вектором r
= СР.
Отношение полуфокального
расстояния (с
) к большой полуоси (а
) называется эксцентриситетом орбиты: . Все планеты и астероиды обращаются вокруг Солнца в направлении движения Земли – с запада на восток. Это так называемое прямое движение. Основные закономерности движения планет полностью определяются законами Кеплера. Рассмотрим эти законы и охарактеризуем основные элементы эллиптических орбит. Согласно первому закону, все планеты обращаются вокруг Солнца по эллиптическим орбитам, в одном из фокусов которых находится Солнце. На рис. 2 показаны элементы планетных орбит с Солнцем (С) в фокусе. Линия АП называется линией апсид, крайние точки которой афелий (А) и перигелий (П) характеризуют наибольшее и наименьшее удаление от Солнца.Расстояние планет( Р ) на орбите от Солнца (гелиоцентрическое расстояние) определяется радиусом-вектором r
= СР.
Отношение полуфокального
расстояния (с
) к большой полуоси (а
) называется эксцентриситетом орбиты: .
Реклама

Если обозначить через q
перигельное
расстояние, а через Q
афелийное
расстояние, то их значения легко определить из выражений: ;
.
Тогда, определив большую полуось (а
), мы найдем среднее годичное расстояние планеты до Солнца:
|  Рис.3.Площади, описываемые радиус-вектором планеты Рис.3.Площади, описываемые радиус-вектором планеты
|
.
Cреднее гелиоцентрическое расстояние Земли от Солнца равно 149,6 млн. км. Эта величина называется астрономической единицей и принимается за единицу измерений расстояний в пределах Солнечной системы.
Согласно второму закону Кеплера радиус-вектор планеты описывает площади, прямо пропорциональные промежуткам времени. Если обозначить через S
1
площадь перигелийного
сектора (рис. 3), а через S
2
– площадь афелийного
сектора, то их отношение будет пропорционально временам Dt
1
и Dt
2
, за которые планета прошла соответствующие отрезки дуг орбиты: .
Отсюда следует, что секториальная скорость :
величина постоянная.
Время, в течение которого планета сделает полный оборот по орбите, называется звездным, или сидерическим периодом Т
(рис. 3). За полный оборот радиус-вектор планеты опишет площадь эллипса:
.
Поэтому секториальная
скорость :
оказывается наибольшей в перигелии, а наименьшей – в афелии. Используя второй закон, можно вычислить эксцентриситет земной орбиты по наибольшему и наименьшему суточному смещению Солнца по эклиптике, отражающему движение Земли . Земля в перигелии пребывает в начале января (h
max
= 61
'), а в афелии в начале июля (h
max
=
57').
По второму закону Кеплера скорость Земли в афелии и перигелии определяется из выражений: ; .
Таким образом, орбита Земли лишь ненамного отличается от окружности.
Найденные из наблюдательной астрономии законы Кеплера показали, что Солнечная система представляет собой механическую систему с центром, находящимся в солнечной массе.
Законы Кеплера послужили Ньютону основой для вывода своего знаменитого закона всемирного тяготения, который он сформулировал так: каждые две материальные частицы взаимно притягиваются с силой, пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними.
Реклама

Математическая формулировка этого закона имеет вид: ,
где M
и m
– взаимодействующие массы, r
– расстояние между ними; G
– гравитационная постоянная. В системе СИ G
= 6,672·10-11
м3
·кг-1
·с-2
. Физический смысл гравитационной постоянной заключается в следующем: она характеризует силу притяжения двух масс весом в 1 кг каждая на расстоянии в 1 м. Величина G
впервые была определена в 1798 г. английским физиком Кавендишем с помощью крутильных весов.
Закон Ньютона решил задачу о характере действия силы, управляющей движением планет. Это сила тяготения, создаваемая центральной массой Солнца. Именно эта сила не дает планетам разлететься, а сохраняет их в связной системе последовательных орбит, по которым как на привязи сотни миллионов лет кружатся большие и малые планеты.
Воспользуемся законом тяготения и определим массу Земли, полагая, что взаимодействуют две массы – Земли (М
) и некоторого тела, лежащего на ее поверхности. Сила притяжения этого тела определяется законом Ньютона: .
Но одновременно из второго закона механики эта же сила равна произведению массы на ускорение:
,
где g –
ускорение силы тяжести; R
– радиус Земли.Приравнивая правые части выражений: ,
найдем выражение для определения массы Земли:
Подставив известные значения G
= 6,672·10-11
м3
·кг-1
·с-2
, g
= 9,81 м/с2
, R
= 6,371·106
м, в итоге получим MЗ
= 5,97·1024
кг, или в граммах: M3
= 5,97·1027
г. Такова масса Земли.
В настоящее время для более точного определения массы и фигуры планет и их спутников используются параметры орбиты искусственных спутников, запускаемых с Земли.
Орбитальные характеристики планет.
Физические условия на поверхности каждой из девяти планет всецело определяются их положением на орбите относительно Солнца. Ближайшие к светилу четыре планеты – Меркурий, Венера, Земля и Марс – имеют сравнительно небольшие массы, заметное сходство в составе слагающего их вещества и получают большое количество солнечного тепла, ощутимо влияющего на температуру поверхности планет. Две из них – Венера и Земля – имеют плотную атмосферу, Меркурий и Марс атмосферы практически не имеют.
Планеты-гиганты Юпитер, Сатурн, Уран и Нептун значительно удалены от Солнца, имеют гигантские массы и плотную мощную атмосферу. Все они отличаются высокой осевой скоростью вращения. Солнечное тепло почти не достигает этих планет. На Юпитере оно составляет 0,018·103
Вт/м2
, на Нептуне – 0,008·103
Вт/м2
.
Большая часть массы вещества Солнечной системы сосредоточена в самом Солнце – более 99%. На долю планет приходится менее 1% общей массы. Остальное вещество рассеяно в астероидах, кометах, метеоритах, метеорной и космической пыли.
Все планеты имеют сравнительно небольшие размеры и в сравнении с расстояниями между ними их можно представлять в виде материальной точки. Из курса физики известно, что произведение массы тела на его скорость называется импульсом: ,
а произведение радиуса-вектора на импульс – моментом импульса: .
Из приведенного выражения видно, что скорость V
движения планеты по эллиптической орбите меняется вместе с изменением радиуса-вектора r.
При этом на основании второго закона Кеплера имеет место сохранение моментов импульса: .
Видно, что при увеличении r
1
скорость V
1
должна уменьшаться, и наоборот (масса т
планеты неизменна). Если выразить линейную скорость V
через угловую скорость w
:
,
то выражение для момента импульса планеты примет вид: 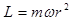 . .
Из последней формулы следует, что при сжатии вращающихся систем, т. е. при уменьшении r
и постоянстве т
, угловая скорость вращения w неизбежно возрастает.
В таблице приведены орбитальные параметры планет. Хорошо видно, как по мере возрастания радиуса орбиты (гелиоцентрического расстояния) уменьшается период обращения и, следовательно, скорость движения планет.
Орбитальные параметры планет Солнечной системы.
| Планета
|
Радиус
орбиты, 109
м
|
Масса,
1027
г
|
Плот-ность,
г/см3
|
Экваториаль-
ный радиус, 106
м
|
Период
вращения, земные сут или ч
|
Наклон экватора к орбите, градусы
|
Период
обращения земные сут
|
| Меркурий
|
57,9
|
0,330
|
5,43
|
2,439
|
58,65 сут
|
2 ± 3
|
87,96935
|
| Венера
|
108,2
|
4,870
|
5,25
|
6,051
|
243,022
(± 006) сут
|
177,3
|
224,7
|
| Земля
|
149,6
|
5,976
|
5,52
|
6,378
|
23,9345 ч
|
23,45
|
365,26
|
| Марс
|
227,9
|
0,642
|
3,95
|
3,393
|
24,6299 ч
|
23,98
|
686,98
|
| Юпитер
|
778,3
|
1900
|
6,84
|
71.398
|
9,841 ч
|
3,12
|
4333
|
| Сатурн
|
1427,0
|
568,8
|
5,85
|
60,33
|
10,233 ч
|
26,73
|
10759
|
| Уран
|
2869,6
|
86,87
|
5,55
|
26,20
|
17,24 ч
|
97,86
|
30685
|
| Нептун
|
4496,6
|
102,0
|
5,60
|
25,23
|
(18,2 ± 0,4) ч
|
(29,56)
|
60189
|
| Плутон
|
5900,1
|
(0,013)
|
(0,9)
|
(1,5)
|
6,387 сут
|
(118,5)
|
90465
|
При движении планеты вокруг Солнца сила притяжения последнего уравнивается центростремительной силой, приложенной к планете: .
Отсюда легко найти среднюю орбитальную скорость движения планеты, которая совпадает с круговой скоростью: ,
где r
= a
– расстояние от Солнца; Т –
период обращения планеты вокруг светила.
В качестве примера найдем среднюю орбитальную скорость вращения Земли, положив в формулу Т
= 365,2564·86400 с = 31,56·106
с, а =
149,6·106
км, получим V
= 29,78 км/с.
Внутренне строение Земли.
Длительное существование воды и жизни на поверхности Земли стало возможным благодаря трем основным характеристикам - ее массе, гелиоцентрическому расстоянию и быстрому вращению вокруг своей оси.
Именно эти планетарные характеристики определили единственно возможный путь эволюции живого и неживого вещества Земли в условиях Солнечной системы, итоги которого запечатлены в неповторимом облике планеты. Эти три важнейшие характеристики у других восьми планет Солнечной системы существенно отличаются от земных, что и явилось причиной наблюдаемых различий в их строении и путях эволюции.
Масса современной Земли равна 5,976·1027
г. В прошлом вследствие непрерывно протекающих процессов диссипации летучих элементов и тепла она, несомненно, была больше. Масса планеты играет определяющую роль в эволюции протовещества. Шарообразная форма Земли свидетельствует о преобладании гравитационной организации вещества в теле планеты.
С ростом глубины растут давление и температура. Вещество переходит в расплавленное и даже ионизованное состояние, благодаря чему возрастает его химический потенциал. Тем самым создаются предпосылки для длительной термической и, следовательно, геологической активности планеты.
Средний радиус гелиоцентрической орбиты Земли (расстояние от Солнца) равен 149,6 млн. км. Эта величина принята в качестве астрономической единицы. Почему мы выделяем этот параметр среди множества других? Дело в том, что на этом расстоянии количество солнечного тепла, достигающего поверхности Земли, таково, что выносимая из недр вода имеет возможность длительное время сохраняться в жидкой фазе, формируя обширные океанические и морские бассейны. Уже на орбите Венеры, расположенной на 50 млн. км ближе к Солнцу, и на орбите Марса, расположенного на 70 млн. км дальше от Солнца, чем Земля, таких условий нет. На Венере из-за избытка солнечного тепла вода испаряется и может существовать только в атмосфере планеты, на Марсе из-за недостатка тепла пребывает в замерзшем состоянии под грунтом планеты (возможно, в форме мерзлоты). И наконец, вращение Земли: полный оборот вокруг своей оси относительно Солнца планета делает за 24 часа, или за 86400 с; относительно звезд - за 86164 с. Благодаря столь быстрому вращению возникли динамические условия, необходимые для образования земного магнитного поля. Без магнитного экрана развитие современных форм жизни при прочих благоприятных условиях было бы невозможно. Поток солнечных частиц высоких энергий беспрепятственно достигал бы земной поверхности, неся гибель живому веществу. Жизнь в этих условиях могла бы зародиться и существовать лишь под водой или глубоко в грунте. Суша являла бы собой мертвые пустыни, лишенные растительности и каких-либо живых существ.
Суточное вращение Земли обеспечивает также попеременное нагревание и охлаждение ее поверхности. Это способствует развитию водной и воздушной циркуляции, ускорению динамики всех процессов жизнедеятельности биосферы, преобразованию вещества земной коры.
Наклон оси вращения к плоскости орбиты (23°27¢) приводит к периодическому (сезонному) изменению количества солнечного тепла, получаемого различными участками земной поверхности при движении планеты по гелиоцентрической орбите. Полное обращение вокруг Солнца Земля делает за 365,2564 звездных суток (сидерический год), или 365,2422 солнечных суток (тропический год).
Площадь поверхности Земли равна 510 млн. км2
, средний радиус сферы - 6371 км.
Земная кора и её строение.
| 
Внутреннее строение Земли. Заштрихованы области внешнего ядра и астеносферы: А - земная кора; ВС - верхняя мантия; D - оболочка; Е - верхнее (жидкое) ядро; F - переходная зона; G - внутреннее ядро
|
Верхняя твердая геосфера именуется земной корой
. Это понятие связано с именем югославского геофизика А.Мохоровичича, который установил, что в верхней толще Земли сейсмические волны распространяются медленнее, нежели на больших глубинах. Впоследствии этот верхний низкоскоростной слой был назван земной корой, а граница, отделяющая земную кору от мантии Земли, - границей Мохоровичича, или, сокращенно, - Моха
. Мощность земной коры изменчива. Под водами океанов она не превышает 10-12 км, а на континентах составляет 40-60 км, (что составляет не более 1% земного радиуса), редко увеличиваясь в горных районах до 75 км. Средняя мощность коры принимается равной 33 км, средняя масса - 3·10 25 г.
По геологическим и геохимическим данным до глубины 16 км подсчитан усредненный химический состав пород земной коры[1]
. Эти данные постоянно уточняются и на сегодня выглядят следующим образом: кислород - 47%, кремний - 27,5, алюминий - 8,6, железо - 5, кальций, натрий, магний и калий - 10,5, на все
 остальные элементы приходится около 1,5%, в том числе на титан - 0,6%, углерод - 0,1, медь - 0,01, свинец - 0,0016, золото - 0,0000005%. Очевидно, что первые восемь элементов составляют почти 99% земной коры и только 1% падает на остальные (более сотни!) элементы таблицы Д.И. Менделеева. Вопрос о составе более глубоких зон Земли остается спорным. Плотность пород, слагающих земную кору, с глубиной возрастает. Средняя плотность пород в верхних горизонтах коры 2,6-2,7 г/см3
, ускорение силы тяжести на ее поверхности 982 см/с2
. Зная распределение плотности и ускорения силы тяжести, можно рассчитать давление для любой точки радиуса Земли. На глубине 50 км, т.е. примерно у подошвы земной коры, давление составляет 13000 атм. остальные элементы приходится около 1,5%, в том числе на титан - 0,6%, углерод - 0,1, медь - 0,01, свинец - 0,0016, золото - 0,0000005%. Очевидно, что первые восемь элементов составляют почти 99% земной коры и только 1% падает на остальные (более сотни!) элементы таблицы Д.И. Менделеева. Вопрос о составе более глубоких зон Земли остается спорным. Плотность пород, слагающих земную кору, с глубиной возрастает. Средняя плотность пород в верхних горизонтах коры 2,6-2,7 г/см3
, ускорение силы тяжести на ее поверхности 982 см/с2
. Зная распределение плотности и ускорения силы тяжести, можно рассчитать давление для любой точки радиуса Земли. На глубине 50 км, т.е. примерно у подошвы земной коры, давление составляет 13000 атм.
Температурный режим в пределах земной коры довольно своеобразен. На некоторую глубину в недра проникает тепловая энергия Солнца. Суточные колебания температуры наблюдаются на глубинах от нескольких сантиметров до 1-2 м. Годовые колебания в умеренных широтах достигают глубины 20-30 м. На этих глубинах залегает слой пород с постоянной температурой - изотермический горизонт
. Его температура равна средней годовой температуре воздуха в данном регионе. В полярных и экваториальных широтах, где амплитуда колебания годовых температур мала, изотермический горизонт залегает близко к земной поверхности. Верхний слой земной коры, в котором температура меняется по сезонам года, называется активным
. В Москве, например, активный слой достигает глубины 20 м.
Ниже изотермического горизонта температура повышается. Повышение температуры с глубиной ниже изотермического горизонта обусловлено внутренним теплом Земли. В среднем прибавка температуры на 1°С осуществляется при заглублении в земную кору на 33 м. Эта величина называется геотермической ступенью
[2]
. Геотермическая ступень в разных регионах Земли различна: полагают, что в зонах вулканизма она может быть около 5 м, а в спокойных платформенных областях - возрастать до 100 м.
Вместе с верхним твердым слоем мантии земная кора объединяется понятием литосфера
, совокупность же коры и верхней мантии принято именовать тектоносферой
.
Типы коры
. В разных регионах соотношение между различными горными породами в земной коре различно, причем обнаруживается зависимость состава коры от характера рельефа и внутреннего строения территории. Результаты геофизических исследований и глубоко бурения позволили выделить два основных и два переходных типа земной коры. Основные типы маркируют такие глобальные структурные элементы коры как континенты и океаны. Эти структуры прекрасно выражены в рельефе Земли, и им свойственны континентальный и океанический типы коры .

Рис. Типы земной коры:
1 - вода, 2 - осадочный слой, 3 - переслаивание осадочных пород
и базальтов, 4 - базальты и кристаллические ультраосновные породы,
5 - гранитно-метаморфический слой, 6 - гранулитово-базитовый слой,
7 - нормальная мантия, 8 - разуплотненная мантия
Континентальная кора
развита под континентами и, как уже говорилось, имеет разную мощность. В пределах платформенных областей, соответствующих континентальным равнинам, это 35-40 км, в молодых горных сооружениях - 55-70 км. Максимальная мощность земной коры - 70-75 км - установлена под Гималаями и Андами. В континентальной коре выделяются две толщи: верхняя - осадочная и нижняя - консолидированная кора.
Океанская кора
характерна для Мирового океана. Она отличается от континентальной по мощности и составу. Мощность ее колеблется от 5 до 12 км, составляя в среднем 6-7 км. Сверху вниз в океанской коре выделяются три слоя: верхний слой рыхлых морских осадочных пород до 1 км мощностью; средний, представленный переслаиванием базальтов, карбонатных и кремнистых пород, мощностью 1-3 км; нижний, сложенный основными породами .
Субокеанская кора
развита под глубоководными котловинами окраинных и внутренних морей (Черное, Средиземное, Охотское и др.), а также обнаружена в некоторых глубоких впадинах на суше (центральная часть Прикаспийской впадины). Мощность субокеанской коры 10-25 км, причем увеличена она преимущественно за счет осадочного слоя, залегающего непосредственно на нижнем слое океанской коры.
Субконтинентальная кора
характерна для островных дуг (Алеутской, Курильской, Южно-Антильской и др.) и окраин материков. По строению она близка к континентальной коре, но имеет меньшую мощность - 20-30 км.
Таким образом, различные типы земной коры отчетливо разделяют Землю на океанические и континентальные блоки. Высокое положение континентов объясняется более мощной и менее плотной земной корой, а погруженное положение ложа океанов - корой более тонкой, но более плотной и тяжелой. Область шельфа подстилается континентальной корой и является подводным окончанием материков.
Газовая оболочка Земли.
Современная атмосфера имеет азотно-кислородный состав: 78,1% – азота, 20,9% – кислорода. В ней также содержится от 0,3 до 3% паров воды, 0,9% аргона и 0,03% углекислого газа. Среди примесей присутствуют неон, криптон, водород, метан и другие газы. Такой состав атмосфера имеет до высоты 100 – 120 км при общей толщине газовой оболочки 1800 – 2000 км.
Атмосфера имеет стратифицированное строение. До высоты 100 – 120 км вследствие активных турбулентных процессов, вызванных температурными контрастами между экватором и полюсами, неравномерным нагреванием земной поверхности солнечным теплом, происходит интенсивное перемешивание воздушных масс. Выше указанной границы происходит гравитационное разделение газов по удельному весу. От 120 до 400 км преобладают молекулярный азот и атомарный кислород. Выше (до высоты 700 км) преобладает атомарный кислород. Внешняя часть атмосферы (до 1000 – 1500 км) имеет преимущественно гелиево-водородный состав. Легкие водород и гелий как бы всплывают над более тяжелой молекулярной оболочкой. Выделяются четыре основных слоя: тропосфера, стратосфера, мезосфера и термосфера (ионосфера) .
Тропосфера.
Это приземный слой атмосферы, простирающийся до высоты 12 – 18 км. В нем содержится до 80% массы всей атмосферы, водяной пар и частицы пыли антропогенного и естественного происхождения (вулканизм, пыльные бури и т.д.). На уровне моря атмосферное давление равно 760 мм ртутного столба, или 1013,32 гПа. С высотой давление падает и на верхней границе тропосферы не превышает 0,026 атм (26 гПа). Тропосфера пронизывается двумя видами солнечной энергии – световой и тепловой. Потоки света и тепла частично рассеиваются облаками и частицами пыли и газов тропосферы, но в основном достигают земной поверхности, нагревая ее до 20 – 40°С. Нагреваясь, Земля переизлучает тепло в атмосферу, но в более длинноволновом диапазоне – инфракрасном. Это тепло поглощается парами воды и углекислого газа. Происходит прогревание тропосферы снизу. Поэтому с высотой температура тропосферы падает в среднем на 6 градусов на километр. Благодаря наклону земной оси к плоскости орбиты и сферичности Земли, количество тепла, получаемое земной поверхностью по долготе – от экватора до полюсов, – сильно меняется. На его распределение оказывают влияние также рельеф, океанические и морские бассейны.
Стратосфера.
От верхней границы тропосферы до высоты 50 – 55 км температура мало меняется и составляет около 220 К. Вследствие вымерзания паров воды в верхних слоях тропосферы в стратосфере почти не происходит поглощения инфракрасного излучения, поступающего снизу. Лучистая теплопроводность стратосферы значительно выше, чем тропосферы. Этим объясняется наблюдаемая стабильность ее температуры. Давление на верхней границе снижается до 3·10-3
атм (3 гПа). Температура несколько повышается до 270 К (около 0°С). Это повышение температуры обусловлено фотохимической реакцией разложения молекулы озона О3
, сопровождающейся выделением тепла. Реакция идет за счет поглощения озоном ультрафиолетового излучения с длиной волны 288,4 нм. Озоновый слой располагается на высоте 20 – 30 км и является последним щитом на пути губительного для биосферы ультрафиолетового излучения. Поэтому указанная высота может рассматриваться как верхняя граница географической оболочки.
Мезосфера.
В промежутке высот 50 – 85 км располагается слой низких температур атмосферы, получивший название «мезосфера». Температура здесь падает до минус 100 – 130°С. В эту область газовой оболочки уже не поступает теплое инфракрасное излучение от земной поверхности. Давление здесь падает до 7·10-5
атм (7 Па).
Термосфера.
Над мезосферой выше 85 км температура начинает расти и на уровне примерно 400 км достигает максимального значения 1000 К. В период солнечной активности она может увеличиваться до 1800 К. Выше 400 км температура не меняется. Термосферу иногда называют ионосферой. Термосфера простирается до высоты 1200 км и далее до 20000 км переходит в протоносферу – водородную корону Земли. Протоносфера почти полностью состоит из ионизованного водорода с незначительной примесью гелия. Плотность газа здесь ничтожно мала, а давление уменьшается до 10-14
атм (10-9
Па).
Закон всемирного тяготения.
На поверхности Земли действует гравитационное поле, создаваемое силой притяжения массы Земли F
и центробежной силой P
, возникающей вследствие вращения Земли вокруг своей оси .
Согласно закону тяготения Ньютона, сила притяжения F
определяется из выражения: , где r
– расстояние от центра Земли до притягиваемой точки;М
– масса Земли;m
– масса притягиваемого тела;G –
гравитационная постоянная, равная в системе СИ: .
Центробежная сила Р
пропорциональна радиусу вращения l
(расстояние от оси вращения) и квадрату угловой скорости w
, где Т
– средние звездные сутки, в течение которых Земля делает полный оборот (на 360°) вокруг своей оси. Таким образом, Р
= w
2
l
cos j
;
рад/с.
На экваторе а = 6,378160×108
см, следовательно, сила, действующая на единицу массы на поверхности земного экватора, будет равна: Р
э
= w
2
а
= 3,391584 гал.
На полюсе lр
= 0 и, следовательно, Рр
= 0.Сила притяжения F
направлена вдоль радиуса r
к центру Земли, сила Р
обратна действию F
. Результирующая этих двух сил и будет определять силу тяжести g
на поверхности Земли: g
= F – Р
, или ,
где l
– расстояние от оси вращения Земли до точечной массы m
на поверхности. Направление вектора g
совпадает с линией отвеса, на конце которого подвешен груз с некоторой массой m
.
Величина g
имеет размерность LT -2
, где L
– длина, Т
– время, т. е. представляет собой ускорение силы тяжести в данной точке земной поверхности. Единицей измерения ускорения силы тяжести в системе СГС служит гал: 1 гал = 1см/с2
. В практике гравитационных наблюдений используется более мелкая величина – миллигал (мгал): 1 мгал= =10-3
гал. Точность современных относительных наблюдений с помощью гравиметров превышает 0,01 мгал, абсолютных наблюдений на стационарных установках – 0,01×10-3
мгал (Мельхиор, 1976).
| Фундаментальные постоянные планет
|
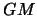 , км , км 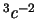
|
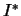
|
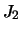
|
| Земля
|
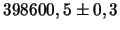
|
0,332
|
0.001082645
|
| Меркурий
|
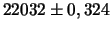
|
|
|
| Венера
|
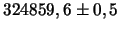
|
0,332
|
0,00000597
|
| Марс
|
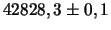
|
0,377
|
0,0008746
|
| Юпитер
|
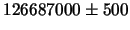
|
0,200
|
0,022060
|
| Сатурн
|
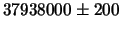
|
0,220
|
0,025010
|
| Уран
|
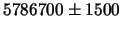
|
0,230
|
|
| Нептун
|
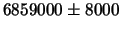
|
0,290
|
|
| Плутон
|
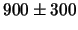
|
|
|
| Луна
|
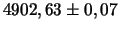
|
0,391
|
0,00009152
|
Форма Земли и гравитация.
| 
|
| Рис. 1.1. Эллипсоид вращения
|
 Первые представления о формах и размерах Земли появились еще в глубокой древности. Античные мыслители (Пифагор - V в. до н.э., Аристотель - III в. до н.э. и др.) высказывали мысль, что наша планета имеет шарообразную форму. Геодезические и астрономические исследования последующих столетий дали возможность судить о действительной форме Земли и ее размерах. Известно, что формирование Земли происходило под действием двух сил - силы взаимного притяжения частиц ее массы и центробежной силы, обусловленной вращением планеты вокруг своей оси. Равнодействующей обеих названных сил является сила тяжести, выражаемая в ускорении, которое приобретает каждое тело, находящееся у поверхности Земли. На рубеже XVII и XVIII вв. впервые Ньютон теоретически обосновал положение о том, что под воздействием силы тяжести Земля должна иметь сжатие в направлении оси вращения и, следовательно, ее форма представляет эллипсоид вращения,
или сфероид.
Степень сжатия зависит от угловой скорости вращения. Чем быстрее вращается тело, тем больше оно сплющивается у полюсов. На рис. 1.1, изображающем эллипсоид вращения, выражена большая экваториальная ось (ЗОВ) и малая полярная ось (СОЮ). Величины а
= ЗОВ/2 и в
= СОЮ/2 соответствуют полуосям эллипсоида. Сжатие эллипсоида будет выражено (а
- в)/а.
Разница полярного и экваториального радиусов составляет 21 км. Детальными последующими измерениями, особенно новыми методами исследования с искусственных спутников, было показано, что Земля сжата не только на полюсах, но также несколько и по экватору (наибольший и наименьший радиусы по экватору отличаются на 210 м), т.е. Земля является не двухосным, а трехосным эллипсоидом. Кроме того, расчетами Т. Д. Жонгловича и С. И. Тропининой показана несимметричность Земли по отношению к экватору: южный полюс расположен ближе к экватору, чем северный.В связи с расчленением рельефа (наличием высоких гор и глубоких впадин) действительная форма Земли является более сложной, чем трехосный эллипсоид. Наиболее высокая точка на Земле - гора Джомолунгма в Гималаях - достигает высоты 8848м. Наибольшая глубина 11 034 м обнаружена в Марианской впадине. Таким образом, наибольшая амплитуда рельефа земной поверхности составляет немногим менее 20 км. Учитывая эти особенности, немецкий физик Листинг в 1873 г. фигуру Земли назвал геоидом, что дословно обозначает "землеподобный". Первые представления о формах и размерах Земли появились еще в глубокой древности. Античные мыслители (Пифагор - V в. до н.э., Аристотель - III в. до н.э. и др.) высказывали мысль, что наша планета имеет шарообразную форму. Геодезические и астрономические исследования последующих столетий дали возможность судить о действительной форме Земли и ее размерах. Известно, что формирование Земли происходило под действием двух сил - силы взаимного притяжения частиц ее массы и центробежной силы, обусловленной вращением планеты вокруг своей оси. Равнодействующей обеих названных сил является сила тяжести, выражаемая в ускорении, которое приобретает каждое тело, находящееся у поверхности Земли. На рубеже XVII и XVIII вв. впервые Ньютон теоретически обосновал положение о том, что под воздействием силы тяжести Земля должна иметь сжатие в направлении оси вращения и, следовательно, ее форма представляет эллипсоид вращения,
или сфероид.
Степень сжатия зависит от угловой скорости вращения. Чем быстрее вращается тело, тем больше оно сплющивается у полюсов. На рис. 1.1, изображающем эллипсоид вращения, выражена большая экваториальная ось (ЗОВ) и малая полярная ось (СОЮ). Величины а
= ЗОВ/2 и в
= СОЮ/2 соответствуют полуосям эллипсоида. Сжатие эллипсоида будет выражено (а
- в)/а.
Разница полярного и экваториального радиусов составляет 21 км. Детальными последующими измерениями, особенно новыми методами исследования с искусственных спутников, было показано, что Земля сжата не только на полюсах, но также несколько и по экватору (наибольший и наименьший радиусы по экватору отличаются на 210 м), т.е. Земля является не двухосным, а трехосным эллипсоидом. Кроме того, расчетами Т. Д. Жонгловича и С. И. Тропининой показана несимметричность Земли по отношению к экватору: южный полюс расположен ближе к экватору, чем северный.В связи с расчленением рельефа (наличием высоких гор и глубоких впадин) действительная форма Земли является более сложной, чем трехосный эллипсоид. Наиболее высокая точка на Земле - гора Джомолунгма в Гималаях - достигает высоты 8848м. Наибольшая глубина 11 034 м обнаружена в Марианской впадине. Таким образом, наибольшая амплитуда рельефа земной поверхности составляет немногим менее 20 км. Учитывая эти особенности, немецкий физик Листинг в 1873 г. фигуру Земли назвал геоидом, что дословно обозначает "землеподобный".
Геоид -
некоторая воображаемая уровенная поверхность, которая определяется тем, что направление силы тяжести к ней всюду перпендикулярно. Эта поверхность совпадает с уровнем воды в Мировом океане, который мысленно проводится под континентами. Это та поверхность, от которой производится отсчет высот рельефа. Поверхность геоида приближается к поверхности трехосного эллипсоида, отклоняясь от него местами на величину 100 - 150 м (повышаясь на материках и понижаясь на океанах, рис. 1.2.), что, по-видимому, связано с плотностными неоднородностями масс в Земле и появляющимися из-за этого аномалиями силы тяжести. В настоящее время принимается эллипсоид Ф. Н. Красовского
и его учеников (А. А. Изотова и др.), основные параметры которого подтверждаются современными исследованиями и с орбитальных станций. По этим данным экваториальный радиус равен 6378,245 км, полярный радиус - 6356,863 км, полярное сжатие- 1/298,25. Объем Земли составляет 1,083 • 1012
км3
, а масса - 6 • 1027
г. Ускорение силы тяжести на полюсе 983 см/с2
, на экваторе 978 см/с2.
Площадь поверхности Земли около 510 млн. км2
, из которых 70,8% представляет Мировой океан и 29,2% - суша. В распределении океанов и материков наблюдается определенная дисимметрия. В Северном полушарии это соотношение составляет 61 и 39%, в Южном-81 и 19%.Фигура Земли в первом приближении представляет собой эллипсоид вращения, у которого экваториальный радиус (а) больше полярного (b) на 21389 км. Отсюда полярное сжатие земного эллипсоида составляет : .
Это различие в длинах радиуса обусловливает современное изменение силы тяжести от полюса до экватора на величину 1,6 гал.Отношение центробежной силы Р
к силе тяготения F
называют геодинамической постоянной q
:
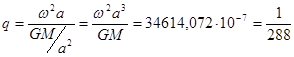 . .
Оно показывает, что сила тяжести на поверхности Земли определяется главным образом притяжением ее массы, а вклад центробежного ускорения составляет всего 0,5%. Тем не менее эта величина действует на протяжении длительного времени, играет исключительно важную роль в дифференциации земного вещества, динамике водных и воздушных масс. Изменение силы Р
по широте и сжатие Земли совместно определяют нормальное изменение поля силы тяжести у Земли.
Для вычислений нормальных значений силы тяжести Земли используются формулы, рассчитанные для эллипсоида вращения в предположении, что Земля состоит из концентрических слоев, однородных по плотности.
Формулы Клеро (1743): G0 = ge(1+βsin2φ-β’sin22φ); β = 5/2q-α; β’ = 1/8α2+1/4αβ,
где: g0 – нормальное значение силы тяжести;
ge – значение силы тяжести на экваторе;
φ – широта пункта наблюдения;
q ≈ 1/300.
Формулы Клеро позволяют вычислить теоретическое значение силы тяжести в какой-либо точке земной поверхности, если известна широта этого пункта. Коэффициенты в формуле Клеро для нормального распределения силы тяжести выводились многими учеными, но практическое применение нашли формула Гельмерта и международная формула Кассиниса.
Формула Гельмерта (1901-1909):
g0 = 978,030(1+0,005302sin2φ-0,000007sin22φ)
Формула Кассиниса:
g0 = 978,049(1+0,0052884sin2φ-0,0000059sin22φ)
Чтобы наблюденные значения силы тяжести, относящиеся к реальной поверхности Земли, сравнивать с нормальными, их необходимо приводить (редуцировать) к уровню эллипсоида. Есть поправка в свободном воздухе, поправка за промежуточный слой, поправка за рельеф.
Аномалии силы тяжести.
Представляя фигуру Земли эллипсоидом вращения и вводя понятие геоида, мы предполагаем, что масса Земли сложена однородным по плотности веществом. При этом изменение силы тяжести на поверхности Земли должно быть обусловлено лишь изменением по широте потенциала центробежной силы и различием в экваториальном и полярном радиусах. Однако в реальных условиях характер изменения силы тяжести отличается от теоретического нормального распределения, рассчитанного для поверхности однородного геоида, или эллипсоида. Такого рода отклонения силы тяжести от нормальной величины вызваны неоднородным распределением плотностей в теле Земли и особенно в верхних ее частях.
Разность между наблюденным ускорением силы тяжести g
и нормальной величиной g
0
, полученной по международной формуле , называется аномалией силы тяжести Dg
: Dg
= g –
g
0
.
Аномалии силы тяжести создаются главным образом неоднородным распределением плотностей в земной коре и верхней мантии. Однако, чтобы выявить эту неоднородность, простого вычитания из наблюденной силы тяжести нормальной составляющей оказывается недостаточно. Дело в том, что величина силы тяжести зависит от целого ряда факторов, и в первую очередь от географической широты и высоты места (относительно уровня моря), рельефа окружающей местности, характера плотностных неоднородностей в верхних слоях Земли под точкой наблюдения и др. Для исключения влияния этих факторов в наблюденное значение Dg
вводят поправки или, как их еще называют, редукции. Название редукции определяет название аномалии силы тяжести.
Аномалия в свободном воздухе, вычисленная с учетом поправки за свободный воздух ,называется аномалией Фая: Δgсв.в. = g-g0+ Δgср.а. Следует отметить, что при введении поправки за свободный воздух влияние масс (плотностных неоднородностей), лежащих между уровнем точки наблюдения и уровнем моря, не учитывается. Однако на самом деле между уровнем наблюдения и уровнем моря залегают породы, обладающие определенной плотностью. Наличие таких пород увеличивает наблюденное значение силы тяжести, и чем выше точка отстоит от уровня моря, тем больше их влияние. Этот эффект наиболее ощутим при наблюдениях в горной местности. На равнине редукция за высоту будет постоянна.
Таким образом, аномалия в свободном воздухе отражает суммарное влияние плотностной неоднородности горных пород и влияние дополнительных масс, вызванное рельефом. Поэтому в условиях расчлененного рельефа с большим перепадом высот (порядка нескольких сотен метров) аномалия в свободном воздухе в значительной степени будет отражать топографию, в то время как гравитационный эффект плотностных неоднородностей верхних этажей геологического разреза Земли будет замаскирован. Исключение, как уже отмечалось, составляют равнинные участки с небольшими перепадами рельефа. В этих условиях аномалия в свободном воздухе может быть использована для изучения глубинной структуры.
Аномалия, вычисленная с поправкой Буге, называется аномалией Буге: ΔgБ = g-g0+ Δgсв.в.- Δgn+ Δgp Обычно плотность берут равной средней плотности земной коры r
= 2,67 г/см3
. Отклонения от этого среднего в реальных разрезах позволяют выявить области с аномальными плотностями.Аномалия в свободном воздухе используется для изучения фигуры Земли. Аномалии Буге позволяют выделять аномальные массы в верхней части земной коры.
Основной фон аномального гравитационного поля определяется рельефом поверхности Мохо, что позволяет расчитать по аномалиям силы тяжести мощность земной коры. Термин аномалии
означает отклонения от некоторой "нормы" -- то есть значения, которое можно предсказать, вычислив его по формуле. Вычисленное значение силы тяжести называют "нормальным", а наблюденное - аномальным. Если принять Землю равновесным эллипсоидом вращения, то значение силы тяжести можно вычислить по формуле:
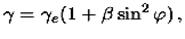
в которой постоянные нужно считать известными. Эти данные определяются из наблюдений и зависят от методики их вычислений, от объема и качества наблюдательных данных. Построение "нормальной" формулы для вычисления силы тяжести требует привлечения экспериментальных данных, полученных в разных странах, в разных экспедициях. В последние 3-4 десятилетия широко используются и спутниковые наблюдения, которые резко увеличили надежность результатов. Для того, чтобы карты гравитационных аномалий, полученных разными авторами, можно было сравнивать и анализировать, необходимо, чтобы гравитационные аномалии вычисляли по одинаковым методикам. По этой причине Международный Геофизический и Геодезический союз на своей Генеральной Ассамблее в августе 1971 года утвердил следующую формулу для нормальной силы тяжести
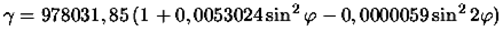
В качестве "нормальной Земли" принят общий земной эллипсоид
с параметрами

Сжатие этого эллипсоида, определенное по спутниковым данным, равно 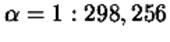 . Известно, что сила тяжести зависит от высоты точки наблюдения. Наблюдения производятся, в крайнем случае, на уровне моря, то есть на высоте, равной нулю. Все сухопутные определения силы тяжести выполняются на разных высотах. Так как поверхность эллипсоида не совпадает с поверхностью уровня, поэтому развита теория приведения гравитационной аномалии (редукции) к одной и той же поверхности. Кроме того, сила тяжести зависит и от масс, лежащих между эллипсоидом и геоидом. Чтобы учесть и эти факторы, развита теория геологических редукций. В таком случае вместе с гравитационными аномалиями обязательно должен указываться и вид редукций, с которыми данная аномалия вычислена. Существуют аномалии в свободном воздухе
, аномалии Фая
, аномалии Буге
, изостатические аномалии и т. п. Гравитационные аномалии на Земле, как правило, меньше 100 мГал
, их среднеквадратическая вариация по Земле составляет величину около 20 мГал
. Следовательно, гравитационное поле Земли достаточно гладкое. Для экстремальных условий (островные дуги, глубоководные впадины) гравитационные аномалии достигают величины 400 мГал
, что в 12,5 раз меньше разницы в значениях силы тяжести на полюсе и экваторе и составляют всего 0,04% от величины силы тяжести. Потому для получения данных, по которым можно судить о внутреннем строении нашей планеты, необходимо изучать аномалии на уровне не только миллигалов, но и микрогалов, чего и добиваются геофизики. Вторая характеристика гравитационного поля -- это отклонение отвесной линии (вертикали) от нормали к эллипсоиду. Это отклонение также невелико и составляет секунды дуги. Геодезические работы в Индии близ горного массива Гималаев показали, что координаты астрономических пунктов из-за отклонений отвесной линии отличаются от геодезических на 5,2", тогда как вычисленное отклонение, связанное с притяжением гор, составляет 27,9". Для объяснения этого явления английский геодезист Пратт высказал мысль, что под горами плотность пород гораздо меньше, чем коренные породы под равнинами. Иными словами, если все породы разбить на блоки, то плотность этих блоков должна зависеть от их толщины: чем толще блок, тем меньше плотность. При этом вес всех блоков на некоторой поверхности, называемой поверхностью компенсации
, один и тот же. Вся земная кора, таким образом, находится в равновесии. Эта гипотеза Пратта получила название изостатической
. Конечно, с геологической точки зрения эта гипотеза никуда не годится. Французский геодезист Эри предложил более правдоподобную схему: земные блоки по Эри подобно айсбергами на море плавают на более плотной, но и более пластичной среде -- верхней мантии. В этом случае, так же как и у айсбергов, должна образоваться под горными массивами "подводная часть" с плотностью, меньшей, чем плотность вмещающих пород. Таким образом эффект гравитационной компенсации должны создавать корни гор
, существование которых сейсмологи подтверждают. Строение земной коры невозможно изучить, пользуясь только одним методом. Геофизики применяют все доступные им методы, прежде всего сейсмологический и гравиметрический. По современным представлениям земная кора имеет разную толщину в разных регионах. В горах толщина ее достигает 60 и более километров. Состоит она из разных слоев. Большой объем занимает кислые (гранитные) породы с плотностью 2,67. Равнины покрыты осадочными породами толщиной несколько километров и с плотностью 2,2. Ниже этих слоев лежат основные породы -- базальты с плотностью 2,8. Толщина коры для равнинных регионов полагают равной 30 км
. Горные районы и равнины образуют основные морфологические особенности континентов. При переходе к океану, гранитный слой постепенно выклинивается, а осадочные породы покрывают на абиссальных котловинах, в основном, базальтовые породы. При этом толщина коры становится меньше и в среднем составляет 10-15 км
. Особенно тонкой кора становится в глубоководных впадинах (4-5 км
). Аномальное гравитационное поле Земли отражает суммарное действие гравитирующих масс, расположенных на различных глубинах в земной коре и верхней мантии. Несмотря на сложную структуру аномального гравитационного поля, наблюдаемого как на суше, так и на море, отдельные участки кривой Dg
могут быть использованы для определения параметров гравитирующей массы. Иногда, меняя форму и глубину залегания гравитирующей массы, рассчитывают создаваемую при этом аномалию. Сравнивая ее с наблюденной аномалией, методом подбора определяют основные параметры возмущающей массы в реальных условиях .Существование гравитационных аномалий над океаническими котловинами и над континентами обусловлено плотностными неоднородностями горных пород. Чем значительнее эти неоднородности, тем лучше они отражаются в аномальном гравитационном поле. Большую роль играют также размеры и форма аномалиеобразующего тела.Для оценки параметров геологических объектов и расчетов создаваемого ими аномального поля силы тяжести вводится понятие избыточной плотности горных пород : . Известно, что сила тяжести зависит от высоты точки наблюдения. Наблюдения производятся, в крайнем случае, на уровне моря, то есть на высоте, равной нулю. Все сухопутные определения силы тяжести выполняются на разных высотах. Так как поверхность эллипсоида не совпадает с поверхностью уровня, поэтому развита теория приведения гравитационной аномалии (редукции) к одной и той же поверхности. Кроме того, сила тяжести зависит и от масс, лежащих между эллипсоидом и геоидом. Чтобы учесть и эти факторы, развита теория геологических редукций. В таком случае вместе с гравитационными аномалиями обязательно должен указываться и вид редукций, с которыми данная аномалия вычислена. Существуют аномалии в свободном воздухе
, аномалии Фая
, аномалии Буге
, изостатические аномалии и т. п. Гравитационные аномалии на Земле, как правило, меньше 100 мГал
, их среднеквадратическая вариация по Земле составляет величину около 20 мГал
. Следовательно, гравитационное поле Земли достаточно гладкое. Для экстремальных условий (островные дуги, глубоководные впадины) гравитационные аномалии достигают величины 400 мГал
, что в 12,5 раз меньше разницы в значениях силы тяжести на полюсе и экваторе и составляют всего 0,04% от величины силы тяжести. Потому для получения данных, по которым можно судить о внутреннем строении нашей планеты, необходимо изучать аномалии на уровне не только миллигалов, но и микрогалов, чего и добиваются геофизики. Вторая характеристика гравитационного поля -- это отклонение отвесной линии (вертикали) от нормали к эллипсоиду. Это отклонение также невелико и составляет секунды дуги. Геодезические работы в Индии близ горного массива Гималаев показали, что координаты астрономических пунктов из-за отклонений отвесной линии отличаются от геодезических на 5,2", тогда как вычисленное отклонение, связанное с притяжением гор, составляет 27,9". Для объяснения этого явления английский геодезист Пратт высказал мысль, что под горами плотность пород гораздо меньше, чем коренные породы под равнинами. Иными словами, если все породы разбить на блоки, то плотность этих блоков должна зависеть от их толщины: чем толще блок, тем меньше плотность. При этом вес всех блоков на некоторой поверхности, называемой поверхностью компенсации
, один и тот же. Вся земная кора, таким образом, находится в равновесии. Эта гипотеза Пратта получила название изостатической
. Конечно, с геологической точки зрения эта гипотеза никуда не годится. Французский геодезист Эри предложил более правдоподобную схему: земные блоки по Эри подобно айсбергами на море плавают на более плотной, но и более пластичной среде -- верхней мантии. В этом случае, так же как и у айсбергов, должна образоваться под горными массивами "подводная часть" с плотностью, меньшей, чем плотность вмещающих пород. Таким образом эффект гравитационной компенсации должны создавать корни гор
, существование которых сейсмологи подтверждают. Строение земной коры невозможно изучить, пользуясь только одним методом. Геофизики применяют все доступные им методы, прежде всего сейсмологический и гравиметрический. По современным представлениям земная кора имеет разную толщину в разных регионах. В горах толщина ее достигает 60 и более километров. Состоит она из разных слоев. Большой объем занимает кислые (гранитные) породы с плотностью 2,67. Равнины покрыты осадочными породами толщиной несколько километров и с плотностью 2,2. Ниже этих слоев лежат основные породы -- базальты с плотностью 2,8. Толщина коры для равнинных регионов полагают равной 30 км
. Горные районы и равнины образуют основные морфологические особенности континентов. При переходе к океану, гранитный слой постепенно выклинивается, а осадочные породы покрывают на абиссальных котловинах, в основном, базальтовые породы. При этом толщина коры становится меньше и в среднем составляет 10-15 км
. Особенно тонкой кора становится в глубоководных впадинах (4-5 км
). Аномальное гравитационное поле Земли отражает суммарное действие гравитирующих масс, расположенных на различных глубинах в земной коре и верхней мантии. Несмотря на сложную структуру аномального гравитационного поля, наблюдаемого как на суше, так и на море, отдельные участки кривой Dg
могут быть использованы для определения параметров гравитирующей массы. Иногда, меняя форму и глубину залегания гравитирующей массы, рассчитывают создаваемую при этом аномалию. Сравнивая ее с наблюденной аномалией, методом подбора определяют основные параметры возмущающей массы в реальных условиях .Существование гравитационных аномалий над океаническими котловинами и над континентами обусловлено плотностными неоднородностями горных пород. Чем значительнее эти неоднородности, тем лучше они отражаются в аномальном гравитационном поле. Большую роль играют также размеры и форма аномалиеобразующего тела.Для оценки параметров геологических объектов и расчетов создаваемого ими аномального поля силы тяжести вводится понятие избыточной плотности горных пород :
 Избыточной плотностью называется разность плотности вмещающих пород r
1
и плотности аномалеобразуюшего тела r
2
. Знание плотности важно при геологическом истолковании гравитационных аномалий. Аномалии Буге даже после тщательного исключения эффектов, обусловленных высотой и видимым рельефом, систематически коррелируют с рельефом по обширным областям. В возвышенных районах они почти всегда отрицательны, над океаническими бассейнами характеризуются большими положительными значениями. Над сушей вблизи уровня моря средняя аномалия Буге близка к нулю, но для обширных областей с высоким рельефом эти аномалии достигают подчас нескольких сотен миллигал. Это может означать, что породы, слагающие возвышенные области, имеют плотность ниже средней, а под океанами плотность пород выше средней. Видимые массы земной поверхности находятся в равновесии. По гипотезе Пратта, чем выше гора, тем меньше ее средняя плотность. Ниже уровня моря земная кора тянется до некоторой постоянной глубины, а ее плотность меняется с изменением высоты рельефа . В качестве геологического подтверждения Пратт постулировал, что горы формировались посредством удлинения вертикальных блоков земной коры без изменения их массы. Поэтому выше некоторого постоянного уровня все эти блоки имеют одну и туже массу. В модели Пратта высота h рельефа земной коры выше уровня моря связана с плотностью коры ρ следующим образом: ρ(H+h) = ρnH, Избыточной плотностью называется разность плотности вмещающих пород r
1
и плотности аномалеобразуюшего тела r
2
. Знание плотности важно при геологическом истолковании гравитационных аномалий. Аномалии Буге даже после тщательного исключения эффектов, обусловленных высотой и видимым рельефом, систематически коррелируют с рельефом по обширным областям. В возвышенных районах они почти всегда отрицательны, над океаническими бассейнами характеризуются большими положительными значениями. Над сушей вблизи уровня моря средняя аномалия Буге близка к нулю, но для обширных областей с высоким рельефом эти аномалии достигают подчас нескольких сотен миллигал. Это может означать, что породы, слагающие возвышенные области, имеют плотность ниже средней, а под океанами плотность пород выше средней. Видимые массы земной поверхности находятся в равновесии. По гипотезе Пратта, чем выше гора, тем меньше ее средняя плотность. Ниже уровня моря земная кора тянется до некоторой постоянной глубины, а ее плотность меняется с изменением высоты рельефа . В качестве геологического подтверждения Пратт постулировал, что горы формировались посредством удлинения вертикальных блоков земной коры без изменения их массы. Поэтому выше некоторого постоянного уровня все эти блоки имеют одну и туже массу. В модели Пратта высота h рельефа земной коры выше уровня моря связана с плотностью коры ρ следующим образом: ρ(H+h) = ρnH,
где ρn – плотность блока коры мощностью H, протягивающегося от уровня моря до глубины компенсации. В соответствии с теорией компенсации Эйри горы имеют под собой «корень» из легкого материала, так что общая масса под горной структурой не больше, чем под соседней низменностью. Чем выше гора, тем глубже «корень» должен проникать в более плотный субстрат.
Глубина компенсации зависит от толщины этого «корня». По Эйри, подошва коры соответствует растянутому зеркальному отражению рельефа поверхности.
Анализируя геоид Жонгловича для двухосного эллипсоида можно сделать выводы, что аномалии гравитационного поля Земли приурочены к континентальным структурам, причем максимумы аномалий располагаются не в центре континентов, а на границах континент-океан. На рисунке видно, что существует пять максимумов аномалий гравитационного поля (три положительных и две отрицательных). Четыре максимума находятся в восточном полушарии и лишь один в западном. Самая интенсивная положительная аномалия (+136) приурочена к западной границе Южной Америки, а самая интенсивная отрицательная (-160) находится на юге Азии.
На рисунке (трехосный эллипсоид) ситуация несколько иная. Аномалии менее интенсивные. Они в восточном полушарии, также как и в случае с двухосным эллипсоидом тяготеют к континентальным структурам, тогда как в западном полушарии максимумы аномалий приурочены как к континентам, так и к океанам. В данном случае выделяются уже восемь максимумов (четыре положительных и четыре отрицательных). Четыре из них расположены в западном полушарии и четыре в восточном. Самая интенсивная положительная аномалия (+85) располагается между Азией и Австралией. Самая интенсивная отрицательная (-77) на юге Азии. На рисунке показана карта высот геоида. Высоты характеризуют уклонения гравитационного поля Земли от нормального поля. Карта показывает, что уклонения не связаны с главными топографическими особенностями Земли (океанами и континентами). Отсюда следует вывод, что континентальные области изостатически скомпенсированы, материки плавают в подкоровом субстрате. Небольшие отклонения гравитационного поля Земли связаны с какими-то изменениями плотности в коре и оболочке.
Максимальное уклонение (73) располагается в районе Индийского океана, минимальные в Тихом.
 
Система Земля – Луна.
Рассмотрим еще одно интересное явление, возникающее под действием взаимного притяжения планеты и обращающегося вокруг нее спутника. Внешним проявлением на Земле этого явления являются приливы и отливы в океане, в ходе которых уровень воды дважды в сутки поднимается и опускается до своих максимальных отметок. Это объясняется притяжением Луны между двумя последовательными одноименными кульминациями ее на меридиане данного места и обусловлено тем, что Земля вращается вокруг своей оси быстрей, чем Луна совершает свой полный оборот вокруг Земли. Поэтому интервал времени между двумя смежными циклами приливных явлений составляет 24 часа 50 мин.
Поясним это на примере . Представим Луну в виде материальной точки, расположенной на расстоянии r
от центра Земли. Радиус планеты положим равным единице, т. е. R
= 1, и рассмотрим, какое притяжение испытывают точки на поверхности Земли (А) на том же меридиане на противоположной стороне (В) и в центре – в точке (О). Пусть эти точки имеют единичную массу. Положив массу Луны m
, для каждой точки в соответствии с законом тяготения можно написать выражения: ; ; .
Найдем разность ускорений силы тяжести материальных точек А и О: .
Поскольку расстояние r
и 2r
много больше единицы, то последними можно пренебречь. В итоге получим: .
Выражение характеризует приливообразующую силу внутри и на поверхности Земли, которая, как видим, обратно пропорциональна кубу расстояний между планетой и ее спутником.
Под действием силы dg
точка А удаляется от точки О в направлении к Луне, образуя своеобразный горб на поверхности планеты – прилив. Но точка О в свою очередь также притягивается Луной на большую амплитуду, чем точка В, расположенная на обратной стороне Земли. Поэтому и на обратной стороне на поверхности планеты образуется приливное вздутие. Одновременно с двумя областями прилива, в точках квадратур, т. е. районах, отстоящих на 90° по меридиану от точек прилива, будет наблюдаться отлив. В ходе вращения Земли приливные волны дважды в сутки обходят ее поверхность. Высота прилива в океане не превышает 1 – 2 м. Однако, когда приливная волна подходит к шельфовому мелководью, она возрастает до нескольких метров. Волны прилива наблюдаются и в твердой коре и достигают 51 см при сложении поля тяготения Луны и Солнца. Приливное трение, возникающее при движении жидкой и в меньшей степени твердой волн, приводит к торможению осевого вращения Земли и ее спутника. По этой причине Луна уже давно прекратила свое вращение вокруг оси и постоянно обращена к планете одной стороной. Уменьшение скорости вращения Земли составляет 2 с за каждые 100 тыс. лет. За последние 450 млн. лет она уменьшилась с 21 часа 53 минут до 24 часов в настоящее время.
Поскольку масса Земли в 81 раз больше массы Луны, то величина приливного ускорения на поверхности спутника будет примерно в 20 раз больше, чем на Земле, и теоретическая высота твердого прилива может достигать нескольких метров.
В связи с этим возникает интересный вопрос о предельно допустимом расстоянии, на которое могут сблизиться спутник и планета в ходе своей эволюции. Для этого приравняем приливной потенциал Земли к ускорению свободного падения на поверхности Луны:
.
После преобразований получим:= 1738»9400 км.
Здесь m
, r
0
– масса и радиус спутника; М
– масса планеты; r
– расстояние между планетой и спутником. Полученное выражение называется пределом Роша. Спутник, попавший внутрь предела Роша вследствие многокилометровой приливной волны, будет неизбежно разрушен и превращен в каменное кольцо вокруг планеты. Не менее катастрофичными станут последствия такого сближения и для планеты. Гигантский приливный горб высотой многие сотни метров, прокатившись многократно по мере сближения спутника по поверхности, перемелет в пыль горы и равнины, реки и моря планеты, а приливное трение раскалит поверхность разрушившихся пород. Резко затормозится скорость вращения планеты, что вызовет изменение ее фигуры и сопутствующие этому процессу землетрясения. Поверхность планеты претерпит катастрофические разрушения. В свете сказанного гипотеза об образовании Тихого океана путем отрыва Луны представляется просто наивной. При входе в зону Роша она была бы превращена в пыль, сквозь которую мы до сих пор не могли бы видеть солнечного света, не говоря уже о том, что в геологической истории Земли подобной катастрофы не запечатлено.
Луна, находясь в поле тяготения Земли (и обе планеты – в поле солнечного притяжения), оказывает воздействие на массу самой Земли. Вследствие больших размеров и массы Земли относительно ее спутника (r
л
/r
з
= 0,27; m
л
/m
з
= 1,2×10-2
) различные точки Земли под влиянием поля тяготения Луны будут испытывать неодинаковые возмущения по отношению к центру массы. Величина этих возмущений зависит от положения тел. В зените (z = 0) или в надире (z = 180°) притяжение максимальное: 0,166 см/с2
для Луны и 0,061 см/с2
– для Солнца; при положении тел в горизонте (z = 90°) притяжение тел минимальное: ‑0,083 см/с2
для Луны и -0,003 см/с2
для Солнца; нулевые значения достигаются при z = 54°44´ и z = 125°16´. Величина статического прилива составляет для Луны от 35,6 до -17,8 см, для Солнца – от 16,4 до ‑8,2 см. Следовательно, размах амплитуды лунных приливов равен 53,4 см, солнечных – 24,6 см; суммарное влияние составляет 78 см (Мельхиор, 1975). Полученные значения теоретической высоты статического прилива верны для жидкой модели Земли. В абсолютно твердой земле никаких деформаций поверхности не происходило бы. Данные непосредственных наблюдений показывают, что высота реального прилива составляет 65 %, или около 51 см от теоретического. Иными словами, земной шар отличается от жидкой модели и от абсолютно твердого тела. Это хорошо согласуется с предыдущими выводами относительно вязкости и жесткости.
В массовом отношении полученный гравитационный эффект равен Dg
/g
» 0,2/106
, т.е. масса в 1 т (106
г) изменяется в результате лунно-солнечного притяжения на 0,2 г. На первый взгляд это незначительная величина, однако если сравнить ее с массой всей Земли, перисферы или гидросферы, наиболее подверженных приливным возмущениям, то получаются внушительные цифры: изменение массы Земли составит 11,948×1020
г (Мз
= 5,974×1027
г), перисферы – 1018
г (Мп
= 9×1025
г), гидросферы – 3,3×1017
г (Мг
= 1,64×1024
г). Если учесть, что эти гигантские массы смещаются в теле Земли регулярно, периодически, на протяжении многих миллионов лет, то становится более понятной роль гравитационного взаимодействия Земли, Луны и Солнца в эволюции протовещества планеты. Представление величины приливного потенциала
в сферической системе координат позволяет разложить его на три лапласовы составляющие, которые получили название зональных, секториальных и тессеральных волн .
Распределение секториальных волн прилива происходит в широтном направлении. Узловые линии, или фронт волны, имеют меридиональное простирание – от полюса до полюса. Максимальная амплитуда прилива достигается на экваторе в полосе шириной от 10° с.ш. до 10° ю.ш. с постепенным уменьшением к полюсам, где функция W
принимает нулевое значение .Положительное значение W
, соответствующее области прилива, функция принимает в зените и надире, отрицательное, соответствующее отливу, – в квадратурах. Доминирующая секториальная волна обозначается индексом M2
. Она имеет полусуточный период (12 ч 25 мин). Этот прилив вызывает внутреннее трение за счет волн, обрушивающихся на протяженную линию побережий Тихого, Атлантического и Индийского океанов, и ответственен за некоторую часть векового замедления скорости вращения Земли. Одновременно с волной M2
появляются еще две лунные волны – N2
и L2
с периодами, близкими к периоду доминирующей волны.
Тессеральный прилив имеет более сложный фронт: узловые линии располагаются по меридиану и экватору. При этом максимум волны достигается на широтах 45° с.ш. и 45° ю.ш. На экваторе и полюсах функция W
= 0. Тессеральному приливу соответствуют главная фаза М
1
и две близкие по периоду волны К
1
и О
1
. Их период равен звездным суткам. Несимметричность тессерального прилива относительно экватора и различная амплитуда его в северном и южном полушариях обусловливают прецессию и нутацию земной оси за счет изменения главного момента инерции Земли.
Зональный прилив зависит только от широты. Его фронтом являются 35° с.ш. и 35°16´ ю.ш. Максимальная амплитуда достигается на полюсах. Поскольку склонение Луны изменяется с периодом 27,321 средних звездных суток, период зонального прилива составляет 14 суток. Зональный прилив определяет сжатие Земли. Перераспределение масс на полюсах и экваторе (прилив на полюсах ведет к образованию отлива на экваторе) приводит к изменению экваториального и полярного моментов инерции, что вызывает изменение главного момента инерции и периодические колебания скорости вращения Земли (Мельхиор, 1975).
В результате вращения узлов лунной орбиты с периодом Т0
= = 18,613 года образуется дополнительная волна прилива, амплитуда которой сравнима с амплитудой месячного прилива. Сложение ее с главной волной зонального прилива приводит к настолько сильному перераспределению масс в теле Земли и перисфере, что это находит выражение в периодичности землетрясений и вулканизма Тихоокеанского подвижного пояса. В частности, прогноз 19-летних циклов составляет до 94 % для сильных землетрясений с магнитудой М ³ 7 и глубиной очагов 0 – 600 км, а также для мощного вулканизма.Кроме перечисленных волн имеются аналогичные им солнечные приливные волны несколько меньшей амплитуды, которые, складываясь с лунными, усиливают их.
Гармонический анализ только месячной серии приливных наблюдений позволяет выделить еще целый ряд волн. В частности, по разложению Дудсона получается 115 секториальных полусуточных, 158 тессеральных суточных, 99 зональных долгопериодных и 14 секториальных третьесуточных волн. Взаимодействие всех этих фаз приводит к сложнейшим взаимным перемещениям возмущающих масс вещества в теле Земли и на поверхности.
Физические основы гравитационных аномалий.
Аномальное гравитационное поле отражает суммарное действие гравитирующих масс, расположенных на различных глубинах в земной коре и верхней мантии. Поэтому для однозначного решения вопроса о природе аномалий необходимо уметь разделять гравитационные поля на региональные, создаваемые глубоко залегающими массами, и локальные, вызванные местными геологическими неоднородностями разреза. В частности, для исключения высокочастотного локального фона пользуются различными методами пересчета аномального поля в верхнее полупространство, т.е. наблюдатель как бы удаляется от объекта возмущений. В результате таких операций мелкие неоднородности поля сглаживаются и остается низкочастотный региональный фон, обусловленный действием глубоко залегающих гравитирующих масс.
Другая задача интерпретации заключается в исключении регионального фона и выделения локальных аномалий, связанных с неглубоко залегающими массами. Методы решения этих задач разработаны довольно обстоятельно и в целом носят полуколичественный характер.
Несмотря на сложную структуру аномального гравиметрического поля, наблюдаемого как на суше, так и на море, отдельные участки кривой Dg
могут быть использованы для определения параметров гравитирующей массы. Иногда, меняя форму и глубину залегания гравитирующей массы, рассчитывают создаваемую при этом аномалию. Сравнивая ее с наблюденной аномалией, методом подбора определяют основные параметры возмущающей массы в реальных условиях.
Нахождение гравитационного поля по известной форме, плотности и глубине залегания гравитирующей массы называется прямой задачей гравиразведки.
Нахождение параметров гравитирующей массы по характеру аномалии называется обратной задачей гравиразведки.
На практике чаще всего приходится решать обратную задачу. При этом наиболее удовлетворительное приближение удается достигнуть для тел простой геометрической формы.
Существование гравитационных аномалий в земной коре, под дном океана, равно как и на суше, обусловлено плотностными неоднородностями горных пород. Чем значительнее эти неоднородности, тем лучше они отражаются в аномальном гравитационном поле. Большое значение имеют также размеры и форма аномалиеобразующего тела.
Для оценки параметров геологических объектов и расчетов создаваемого ими аномального поля силы тяжести вводится, как уже говорилось, понятие избыточной плотности горных пород:
.
Избыточной плотностью называется разность плотности вмещающих пород r
1
и плотности аномалиеобразующего тела r
2
. Знание плотности важно при геологическом истолковании гравитационных аномалий.
Сведения о плотностях горных пород получают различными способами: непосредственными измерениями в скважинах или по образцам, или косвенным путем по данным о сейсмических скоростях распространения волн в толщах пород, или аналитически по наблюденным гравитационным аномалиям.
Плотность горной породы определяется как отношение массы вещества m
к ее объему V
:
Она зависит от минералогического состава, пористости и влажности породы. Чем больше пористость, тем меньше плотность, и наоборот. Если поры заполнены водой, то плотность такой породы повышается. Различные геологические процессы оказывают существенное влияние на плотность пород. Например, в зонах тектонических разломов в результате дробления пород и замещения их более легкими породами может происходить разуплотнение первоначально более плотного субстрата. В случае внедрения интрузий основного или ультраосновного состава происходит замещение менее плотных пород более плотными. Увеличение плотности пород наблюдается в сводах антиклинальных складок в результате сжатия пород.В целом плотность осадочных пород меньше, чем плотность магматических и метаморфических пород, и возрастает с увеличением основности пород. Ниже приведены плотности наиболее распространенных пород.
Плотности наиболее распространенных пород.
| Порода
|
Средняя плотность, г/см3
|
| Глинистые сланцы
|
Метаморфические
|
2,3
|
| Серпентиниты
|
|
2,6
|
| Граниты
|
Кислые
|
2,7
|
| Диабазы, габбро
|
Основные
|
2,9
|
| Базальты
|
|
3,0
|
| Дуниты
|
Ультраосновные
|
3,2
|
| Глины
|
|
2,0
|
| Песчаники
|
Осадочные
|
2,3
|
| Известняки
|
|
2,5
|
| Морская вода
|
–
|
1,03
|
В реальных средах наблюдаются довольно значительные отклонения плотности от указанных средних значений в ту или иную сторону.
Сопоставление плотности с другими физическими свойствами горных пород обнаруживает в ряде случаев определенные статистические связи. Так, отмечается параболическая зависимость скорости распространения продольных сейсмических волн от плотности. С увеличением скорости плотность закономерно возрастает. Это позволяет проводить оценку плотностных характеристик геологического разреза по материалам сейсмических исследований. Выше приводились данные об увеличении плотности пород по мере повышения их основности. В этом же направлении происходит и увеличение магнитной восприимчивости пород, хотя более определенной статистической закономерности здесь определить не удается.
Плотность горных пород дна океана в большинстве случаев удается определить на образцах, драгированных лишь с поверхности дна. Начавшееся в 1969 г. глубоководное бурение с «Гломар Челленджер» позволило проводить непосредственные определения плотности осадочных и базальтовых пород на глубину до 1 км под поверхность дна океана.
Измерения плотности на образцах производятся либо путем гидростатического взвешивания, либо с помощью специального прибора – денситометра. В первом случае значение плотности непористых образцов определяется по формуле : ,
где P
1
и P
2
– вес образца соответственно в воздухе и в воде. При измерениях на денситометре значение плотности r отсчитывается по шкале прибора, отградуированной в г/см3
.Чем детальнее нам нужно знать гравитационное поле, тем большее число параметров определяют аналитическое выражение для силовой функции поля тяготения планеты. В эпоху, когда спутники еще были недоступны,основным методом исследования гравитационного поля был гравиметрический. Гравиметрия
-- область геофизики, изучающая способы наиболее высокоточного определения удельной силы тяжести и ее геологической интерпретации. Этой наукой занимаются как физики, механики так и геологи. До 20-х годов ХХ столетия наука не располагала средствами для измерения удельной силы тяжести на морях и океанах с точностью достаточной, для ее геологического истолкования. В 1922-1929 гг голландский ученый-геодезист Венинг-Мейнес разработал способ наблюдения колебаний маятников на слабо качающемся основании. Используя подводную лодку в качестве лаборатории, он совершил ряд плаваний в Юго-Восточную Азию, исследовал регион, содержащий островные дуги и глубоководные впадины. Идеи Венинг-Мейнеса были реализованы в Государственном астрономическом институте им. П.К. Штернберга профессором Л.В.Сорокиным. До Великой Отечественной войны Л.В,Сорокин с учениками совершил ряд плаваний на подводных лодках на Черном море, в Баренцовом, Охотском и Беринговом морях. Только война остановила эти исследования. Однако, после войны они вновь активизировались. Были разработаны и другие методы для измерения силы тяжести на обычных исследовательских судах, были изобретены морские гравиметры, способные измерять приращение силы тяжести с относительной точностью не хуже  . В морских гравиметрических исследованиях после войны принимали активное участие и другие страны, в частности США, Англия, Германия, Франция, Италия и Япония. Они и сейчас продолжают активное исследование гравитационных полей акваторий, в особенности нефтегазоносных акваторий. Накопился достаточно большой материал для определения модели гравитационного поля Земли как планеты. По мере накопления новых данных производилась ревизия этих моделей. Одна из последних моделей гравитационного поля по геофизическим данным была построена в ГАИШ профессором Н.П. Грушинским. Настоящую революцию в определении гравитационного поля планеты произвели первые запуски искусственных спутников Земли. Был отмечен резкий скачек в точности определения постоянной . В морских гравиметрических исследованиях после войны принимали активное участие и другие страны, в частности США, Англия, Германия, Франция, Италия и Япония. Они и сейчас продолжают активное исследование гравитационных полей акваторий, в особенности нефтегазоносных акваторий. Накопился достаточно большой материал для определения модели гравитационного поля Земли как планеты. По мере накопления новых данных производилась ревизия этих моделей. Одна из последних моделей гравитационного поля по геофизическим данным была построена в ГАИШ профессором Н.П. Грушинским. Настоящую революцию в определении гравитационного поля планеты произвели первые запуски искусственных спутников Земли. Был отмечен резкий скачек в точности определения постоянной 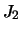 -- постоянной, ответственной за сжатие планеты -- одним из основных параметров, необходимых для развертывания карт на Земной поверхности. Сейчас разработаны новые методы наблюдения ИСЗ, которые позволяют определить положение спутника с точностью -- постоянной, ответственной за сжатие планеты -- одним из основных параметров, необходимых для развертывания карт на Земной поверхности. Сейчас разработаны новые методы наблюдения ИСЗ, которые позволяют определить положение спутника с точностью  2 см
. Возникло новое направление небесной механики, позволяющее по видимым неравенствам в движении спутника определять возмущающие силы – гравитационное поле планеты. Как известно обратные задачи динамики относятся к типу некорректных, теорию которых разработали ученые МГУ и успешно используются для решения задач как геофизики, так и астрофизики. Сейчас построено достаточно много моделей гравитационного поля Земли разной детальности и точности. Отмечено, что с увеличением степени и порядка разложения падает точность определения коэффициентов. Для описания регионального поля часто прибегают к модели степени и порядка 36 (36х36). Наиболее детальная из известных моделей, по-видимому, модель, получившая шифр EGM-96 (360х360). 2 см
. Возникло новое направление небесной механики, позволяющее по видимым неравенствам в движении спутника определять возмущающие силы – гравитационное поле планеты. Как известно обратные задачи динамики относятся к типу некорректных, теорию которых разработали ученые МГУ и успешно используются для решения задач как геофизики, так и астрофизики. Сейчас построено достаточно много моделей гравитационного поля Земли разной детальности и точности. Отмечено, что с увеличением степени и порядка разложения падает точность определения коэффициентов. Для описания регионального поля часто прибегают к модели степени и порядка 36 (36х36). Наиболее детальная из известных моделей, по-видимому, модель, получившая шифр EGM-96 (360х360).
Первая в мире гравикарта.
Такой карты не было еще никогда. Переливы цветов показывают еле уловимые изменения гравитационного поля Земли. Если бы вам пришлось пролетать над красными зонам, вас бы тянуло вниз чуть сильнее, а голубым обозначены области, где притяжение планеты слегка ослабевает. Гравитационные аномалии не воспринимаются человеческими органами чувств, поэтому ученые нанесли эти данные на сферу, преувеличив пики и провалы. Так была получена удивительно четкая иллюстрация предмета исследования. Выглядит она, возможно, несколько странно, но не надо обольщаться – эта карта и те, что последуют за ней, позволят получить новые сведения о том, как океаны движутся и влияют на климат. Само понимание того, как парниковые газы могут изменить планету, будет зависеть от этих пиков и впадин. Карта была составлена совместной американо-германской экспедицией Grace (Эксперимент по реверсии гравитации и климата).  Карта – первый продукт проекта, в котором участвуют два спутника, находящихся в 450 км от Земли. Спутники собирают информацию, выполняя тщательно выверенные маневры на орбите. В то время как один покачивается и медленно перемещается в неровном гравитационном поле земли, второй, следующий на расстоянии 220 километров, измеряет колебания в разделяющем их расстоянии вплоть до микрона. Именно изменения расстояния и описывают природу и масштабы гравитационных аномалий, над которыми пролетают спутники. Очевидные пики гравитации были известны уже некоторое время - например, Гималаи, где масса продолжает накапливаться вместе с гравитационным притяжением, в то время как порода собирается в этой области в результате перемещения тектонических плит Земли. Но собрать подробности удалось только с помощью Grace, особенно в отношении океанов, которые образует постоянно перемещающаяся водная масса. Первая карта, созданная Grace, статична – своего рода "гравитационный слепок" Земли. Но этот профиль постоянно изменяется – вместе с движениями земной коры, океанов и атмосферы над ними. Теперь Grace будет раз в 30 дней присылать на Землю новый профиль, из которых в будущем можно будет составить динамическую модель и следить за изменениями. Карта – первый продукт проекта, в котором участвуют два спутника, находящихся в 450 км от Земли. Спутники собирают информацию, выполняя тщательно выверенные маневры на орбите. В то время как один покачивается и медленно перемещается в неровном гравитационном поле земли, второй, следующий на расстоянии 220 километров, измеряет колебания в разделяющем их расстоянии вплоть до микрона. Именно изменения расстояния и описывают природу и масштабы гравитационных аномалий, над которыми пролетают спутники. Очевидные пики гравитации были известны уже некоторое время - например, Гималаи, где масса продолжает накапливаться вместе с гравитационным притяжением, в то время как порода собирается в этой области в результате перемещения тектонических плит Земли. Но собрать подробности удалось только с помощью Grace, особенно в отношении океанов, которые образует постоянно перемещающаяся водная масса. Первая карта, созданная Grace, статична – своего рода "гравитационный слепок" Земли. Но этот профиль постоянно изменяется – вместе с движениями земной коры, океанов и атмосферы над ними. Теперь Grace будет раз в 30 дней присылать на Землю новый профиль, из которых в будущем можно будет составить динамическую модель и следить за изменениями.
__________________________________________________________________________________________
Список использованной литературы
1. Учебник по геофизике – 2000 г. – Орлёнок Ю.А.
2. Сборник статей по гравитационным аномалиям факультета геологии МГУ.
3. Международный бюллетень по гравиразведки - 2002 г.
[1]
Значения средних содержаний отдельных элементов названы кларками - по фамилии впервые рассчитавшего их в 1889 г. американского ученого Ф. Кларка.
[2]
Величина, обратная геотермической ступени, называется геотермическим градиентом, т.е. градиент - это число градусов, на которое увеличивается температура на каждые 100 м глубины.
|