Л
екция 10.Криволинейные интегралы первого и второго рода, их свойства и вычисление.
Рассмотрим на плоскости или в пространстве кривую L и функцию f, определенную в каждой точке этой кривой. Разобьем кривую на части Δsi длиной Δsi и выберем на каждой из частей точку Mi. Составим интегральную сумму 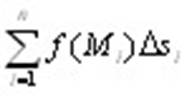 . Назовем λ длину наибольшего отрезка кривой. . Назовем λ длину наибольшего отрезка кривой.
Определение 10.1. Если существует конечный предел интегральной суммы 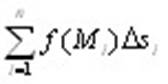 , не зависящий ни от способа разбиения кривой на отрезки, ни от выбора точек Mi, то он называется криволинейным интегралом первого рода от функции f по кривой L и обозначается , не зависящий ни от способа разбиения кривой на отрезки, ни от выбора точек Mi, то он называется криволинейным интегралом первого рода от функции f по кривой L и обозначается
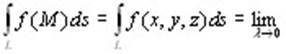 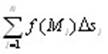 . (10.1) . (10.1)
Например, если функция f(M) задает плотность в точке М, то интеграл (10.1) равен массе рассматриваемой кривой.
Свойства криволинейного интеграла 1-го рода.
1. Если функция f непрерывна на кривой L, то интеграл 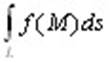 существует. существует.
2. Криволинейный интеграл 1-го рода не зависит от направления движения по кривой, то есть от того, какую из точек, ограничивающих кривую, считать начальной, а какую – конечной. Если назвать эти точки А и В, то
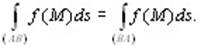 (10.2) (10.2)
Справедливость этих свойств следует из определения криволинейного интеграла 1-го рода.
Способ вычисления криволинейного интеграла 1-го рода.
Выберем на кривой L направление от начальной точки А и отметим, что положение точки М на кривой определяется длиной дуги АМ = s. Тогда кривую L можно задать параметрически: x = x(s), y = y(s), z = z(s), где 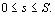 Функция f(x,y,z) становится при этом сложной функцией одной переменной s: f(x(s), y(s), z(s)). Тогда интегральная сумма Функция f(x,y,z) становится при этом сложной функцией одной переменной s: f(x(s), y(s), z(s)). Тогда интегральная сумма
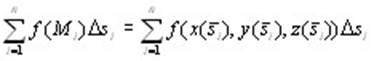 , ,
где 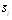 - координата точки Mi, является обычной интегральной суммой для определен-ного интеграла - координата точки Mi, является обычной интегральной суммой для определен-ного интеграла 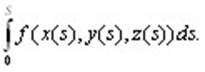 Следовательно, Следовательно,
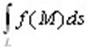 = = 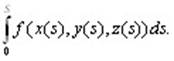 (10.3) (10.3)
Если же кривая L задана в параметрической форме:
x = φ(t), y = ψ(t), z = χ(t), t0 ≤ t ≤ T,
то, применяя в интеграле (10.3) формулу замены переменной и учитывая, что дифференциал дуги
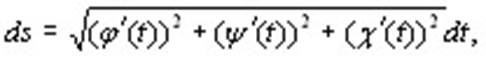
получим:
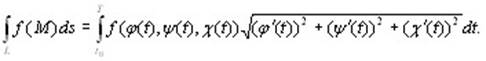 (10.4) (10.4)
Таким образом, вычисление криволинейного интеграла 1-го рода сводится к вычислению обычного определенного интеграла от функции переменной t в пределах, соответствующих изменению значения этой переменной на рассматриваемой кривой.
Пример.
Вычислить 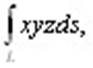 где L: где L: 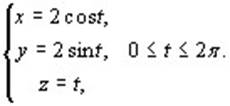 Применяя формулу (10.4), получим: Применяя формулу (10.4), получим:
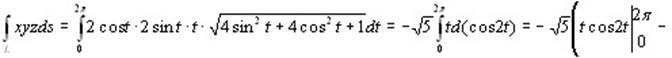
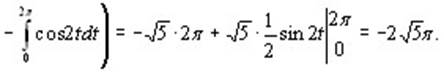
Криволинейный интеграл второго рода.
Вновь рассмотрим кривую L, в каждой точке которой задана функция f(M), и зададим разбиение кривой на отрезки. Выберем на каждом отрезке точку Mi и умножим значе-ние функции в этой точке не на длину i-го отрезка, как в случае криволинейного инте-грала 1-го рода, а на проекцию этого отрезка, скажем, на ось Ох, то есть на разность xi – xi-1 = Δxi. Составим из полученных произведений интегральную сумму 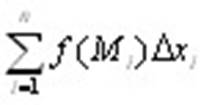 . .
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение
Определение 10.2. Если существует конечный предел при 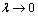 интегральной суммы интегральной суммы 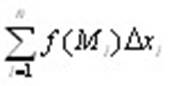 , не зависящий от способа разбиения кривой на отрезки и выбора точек Mi, то от называется криволинейным интегралом второго рода от функции f(M) по кривой L и обозначается , не зависящий от способа разбиения кривой на отрезки и выбора точек Mi, то от называется криволинейным интегралом второго рода от функции f(M) по кривой L и обозначается
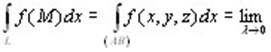 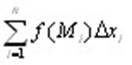 . (10.5) . (10.5)
Подобным образом можно определить и криволинейные интегралы 2-го рода вида
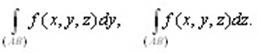
Определение 10.3. Если вдоль кривой L определены функции P(M) = P(x, y, z),
Q(M) = Q(x, y, z), R(M) = R(x, y, z) и существуют интегралы
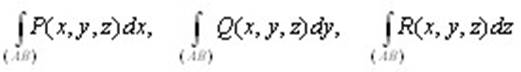 , ,
то и их сумму называют криволинейным интегралом второго рода (общего вида) и полагают
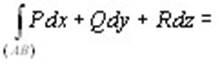 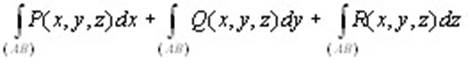 . (10.6) . (10.6)
Замечание. Если считать, что сила 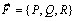 действует на точку, движущуюся по кривой (АВ), то работа этой силы может быть представлена как действует на точку, движущуюся по кривой (АВ), то работа этой силы может быть представлена как
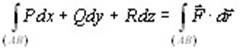 , ,
то есть криволинейным интегралом 2-го рода.
Свойства криволинейного интеграла 2-го рода.
1. Если функции P(M), Q(M), R(M) непрерывны на кривой (АВ), то интеграл (10.6) существует (справедливость этого утверждения следует из определения 10.2).
1. При изменении направления кривой (то есть перемены местами начальной и конечной ее точек) криволинейный интеграл 2-го рода меняет знак:
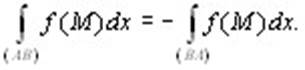 (10.7) (10.7)
Действительно, при этом изменяется знак Δxi в интегральной сумме.
Способ вычисления криволинейного интеграла 2-го рода.
Теорема 10.1. Пусть кривая L задана параметрическими уравнениями
x = φ(t), y = ψ(t), z = χ(t), α ≤ t ≤ β ,
где φ, ψ, χ – непрерывно дифференцируемые функции, и на ней задана непрерывная функция f(x, y, z). Тогда интеграл (10.5) существует и имеет место равенство
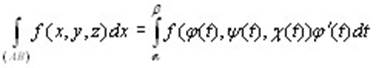 . (10.8) . (10.8)
Доказательство.
Запишем Δxi = xi – xi-1 = φ(ti) – φ(ti-1) и преобразуем последнюю разность по формуле Лагранжа: φ(ti) – φ(ti-1) = φ΄(τi)Δti, где τi – некоторое значение t, заключенное между ti-1 и ti. Выберем точку Мi так, чтобы ее координаты соответствовали значению параметра, равному τi : Mi(φ(τi), ψ(τi), χ(τi)). Подставив эти значения в формулу (10.5), получим:
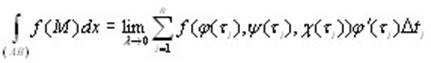 . .
Справа получен предел интегральной суммы для функции f(φ(t),ψ(t),χ(t))φ΄(t) на отрезке [α, β], равный определенному интегралу от этой функции:
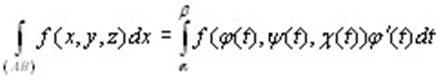 , ,
что и требовалось доказать.
Следствие. Аналогичные соотношения можно получить для криволинейных интегра-лов вида 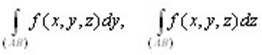 , откуда следует, что , откуда следует, что

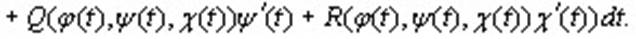 (10.9) (10.9)
Пример.
Сервис онлайн-записи на собственном Telegram-боте
Попробуйте сервис онлайн-записи VisitTime на основе вашего собственного Telegram-бота:
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно.
Зарегистрироваться в сервисе
Вычислим интеграл 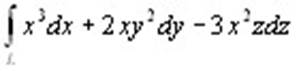 , где L – отрезок прямой от точки А(1,2,-2) до точки В(0, -1, 0). Запишем уравнение этой прямой в параметрическом виде: , где L – отрезок прямой от точки А(1,2,-2) до точки В(0, -1, 0). Запишем уравнение этой прямой в параметрическом виде:
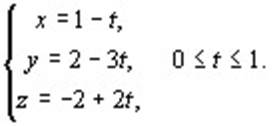
Следовательно, φ΄(t) = -1, ψ΄(t) = -3, χ΄(t) = 2. Тогда
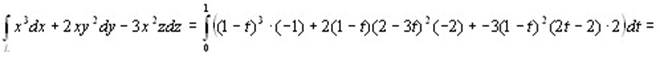
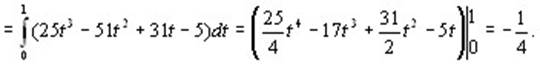
|