|
СМО с отказами (задача Эрланга)
Рассматривается N-канальная СМО с отказами:
λпотерь
λобслуживания
υ
υ
υ
λ
ОА1
ОА2
ОАn
G
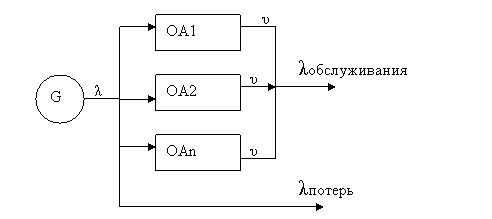
Любая заявка может быть обслужена любым свободным каналом. Если все каналы заняты, заявка немедленно получает отказ в обслуживании и покидает систему (теряется). Интенсивности входных и выходных потоков:
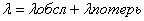
Считаем, что в этой системе имеются следующие потоки событий:
1)
поступление заявок на вход СМО из источника заявок G;
2)
обслуживание заявок в каналах.
Будем считать, что первый и второй потоки событий являются простейшими потоками с экспоненциальными законами распределения. Интервал поступления и обслуживания заявок соответственно имеют следующие характеристики:
1)
интенсивность потока поступающих заявок характеризуется λ
2)
интенсивность обслуживания одним каналом:
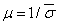
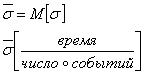
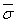 - мат.ожидание длительности обслуживания - мат.ожидание длительности обслуживания
Т.о. входной поток с интенсивностью λ и поток обслуживания с интенсивностью µ распределены по экспоненциальному закону и следовательно данные потоки являются простейшими, а сами процессы в системе Марковскими. Представим граф схему переходов для этого случая:
Состояния СМО в данном случае нумеруются по числу заявок, находящихся в СМО (в силу отсутствия очереди состояния, в котором находится система, совпадает с числом занятых каналов)
S0 - все каналы свободны, система свободна
S1 - занят один канал
Sk - заняты k каналов, остальные (n-k) свободны
Sn - заняты все n каналов
µ
2µ
(n-1)µ
nµ
λ
λ
λ
λ
λ
λ
S0
S1
S2
Sk
Sn-1
Sn

Из состояния Si-1 всегда с интенсивностью входного потока λ система переходит в следующее состояние Si, т.е. в данном случае будет заняе еще один канал и интенсивность перехода в следующее состояние равно интенсивности входного потока λ. Интенсивность обратного перехода возрастает с ростом числа параллельно работающих каналов. Чем больше их работает, тем интенсивнее процесс их освобождения. Для простейших потоков имеем:
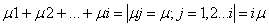
Данная схема называется схемой гибели и размножения. Такое название происходит от того, что связаны соседние состояния. Математический аппарат - это Марковский процесс, с дискретными состояниями и непрерывным временем. Для заданной СМО матрица интенсивностей Λ имеет вид:
Реклама

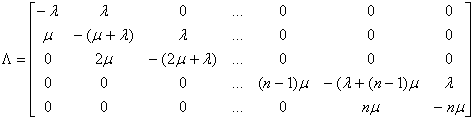
Пользуясь матрицей Λ запишем уравнения, которые позволяют рассчитать вероятности пребывания системы в каждом из указанных состояний. Распределение вероятностей P0,P1,…,Pn по состояниям S0,…,Sn определяется как решение системы дифференциальных уравнений.
P’(t)=P(t)Λ с начальными условиями:
P0(0)=1
Pi(0)=0, i=1,n;
Эти уравнения называются уравнениями Эрланга. Вероятности Рi характеризуют среднюю загрузку системы, в частности, Pn - это вероятность получения отказа в обслуживании, т.е. вероятность того, что все каналы заняты и все поступающие заявки будут потеряны. Тогда q=1-Pn - это вероятность обслуживания.
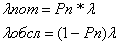
Зная эти вероятности, можно рассчитать различные характеристики эффективности системы.
А - среднее число заявок, обслуживаемых СМО в единицу времени или абсолютная пропускная способность СМО
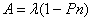
Q - относительная пропускная способность СМО или вероятность обслуживания поступившей заявки

|