Введение
Методы теории сравнений широко применяются в различных областях науки, техники, экономики. Этот раздел алгебры занимает важное место в вузовском образовании математиков, физиков и других специалистов, однако очень часто изучается недостаточно глубоко. Задача данной курсовой работы – изучить теоретический материал и рассмотреть ряд основополагающих задач по одному из основных разделов теории чисел: сравнения первой степени с одной и несколькими переменными, сравнения высших степеней и т.д.
Основная часть курсовой работы состоит из трех глав. В первой главе раскрываются основные понятия теории сравнений, такие как сравнения в кольце целых чисел, основные теоремы и свойства сравнений. Во второй главе рассматриваются сравнения первой степени с одной переменной. Далее рассматриваются сравнения высших степеней и системы сравнений первой степени. В приложении приводятся примеры решения текстовых задач, которые сводятся к неопределенным уравнениям первого порядка и решаются с помощью сравнений.
Изложение теоретического материала иллюстрируется большим количеством примеров с подробными решениями.
В работе приводится список литературы по теме.
1. Теория сравнений
1.1 Сравнения в кольце целых чисел
Понятие сравнения было введено впервые Гауссом. Несмотря на свою кажущуюся простоту, это понятие очень важно и имеет много приложений.
Возьмем произвольное фиксированное натуральное число  и будем рассматривать остатки при делении на m
различных целых чисел. При рассмотрении свойств этих остатков и произведении операций над ними удобно ввести понятие так называемого сравнения по модулю. и будем рассматривать остатки при делении на m
различных целых чисел. При рассмотрении свойств этих остатков и произведении операций над ними удобно ввести понятие так называемого сравнения по модулю.
Определение
. Целые числа 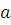 и и 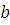 называются сравнимыми по модулю называются сравнимыми по модулю  , если разность , если разность 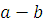 делится на делится на  , т.е. если , т.е. если 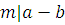 . .
Таким образом, сравнение представляет собой соотношение между тремя числами 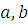 и и  , причем , причем  , играющее роль своего рода эталона сравнения, мы называем «модулем». Для краткости будем это соотношение между , играющее роль своего рода эталона сравнения, мы называем «модулем». Для краткости будем это соотношение между 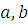 и и  записывать: записывать:
| 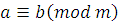 , ,
|
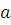 и и 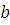 будем называть соответственно левой и правой частями сравнения. Число будем называть соответственно левой и правой частями сравнения. Число  , стоящее под знаком модуля, будем всегда считать положительным, т.е. запись , стоящее под знаком модуля, будем всегда считать положительным, т.е. запись 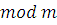 будет означать, что будет означать, что 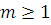 . .
Если разность 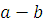 не делится на не делится на  , то мы будем записывать: , то мы будем записывать:
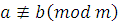 . .
Согласно определению, 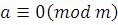 означает, что означает, что 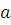 делится на делится на  . .
Примеры
.
1. 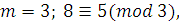 так как так как 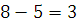 и и 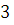 делится на делится на 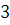 . .
2. 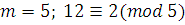 , так как , так как 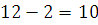 и и 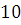 делится на делится на 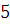 . .
3. 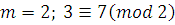 , так как , так как 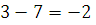 и и 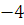 делится на делится на 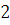 . .
1.2 Основные теоремы о сравнениях
Теорема 1 (признак сравнимости двух чисел по модулю
 ).
Два целых числа ).
Два целых числа 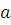 и и 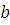 сравнимы по модулю сравнимы по модулю  тогда и только тогда, когда тогда и только тогда, когда 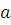 и и 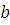 имеют одинаковые остатки при делении на имеют одинаковые остатки при делении на  . .
Доказательство
. Пусть остатки при делении 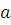 и и 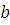 на на  равны, т.е. равны, т.е.
| 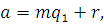
|
(1.1)
|
| 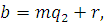
|
(1.2)
|
где 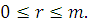
Вычтем (1.2) из (1.1); получим 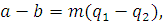 т.е. т.е. 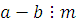 или или 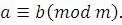
Обратно, пусть 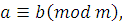 это означает, что это означает, что 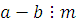 или или
| 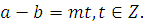
|
(1.3)
|
Разделим 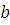 на на  ; получим ; получим 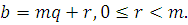 Подставив Подставив 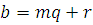 в (1.3), будем иметь в (1.3), будем иметь 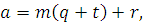 т.е. при делении т.е. при делении 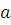 на на  получается тот же остаток, что и при делении получается тот же остаток, что и при делении 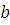 на на  . .
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение
Пример 1
. Определим, сравнимы ли числа 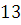 и и 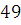 по модулю по модулю 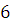 . .
Решение. При делении 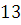 и и 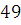 на на 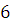 получаются одинаковые остатки получаются одинаковые остатки 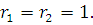 Следовательно, Следовательно, 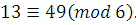
Определение
. Два или несколько чисел, дающие при делении на  одинаковые остатки, называются равноостаточными или сравнимыми по модулю одинаковые остатки, называются равноостаточными или сравнимыми по модулю  . .
Теорема 2
. Отношение сравнимости рефлексивно: 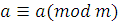 . .
Доказательство
. 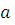 и и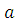 имеют одинаковые остатки при делении на имеют одинаковые остатки при делении на  . .
Теорема 3
. Отношение сравнимости симметрично: если 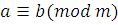 , то , то 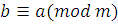 . .
Доказательство
. Если 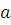 и и 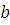 имеют одинаковые остатки при делении на имеют одинаковые остатки при делении на  , то остатки от деления , то остатки от деления 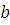 и и 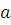 на на  также равны. также равны.
Теорема
4
. Отношение сравнимости транзитивно: если 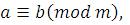
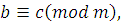 то то 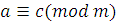 . .
Доказательство
. Если остатки от деления на  одинаковы у чисел одинаковы у чисел 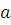 и и 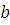 , а также у , а также у 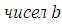 и и 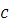 ,
то ,
то 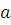 и и 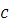 тоже имеют одинаковые остатки при делении на тоже имеют одинаковые остатки при делении на  . .
Таким образом, отношение сравнимости есть отношение эквивалентности.
Теорема 5
. Если 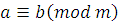 и и 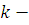 произвольное целое число, то произвольное целое число, то
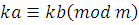 . .
Доказательство
. Если 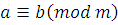 , то , то 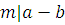 , ,
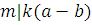 , ,
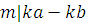 , , 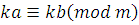 . .
Теорема 6
. Если 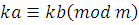 и и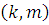 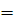 1
, то 1
, то  . .
Доказательство
. Если 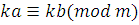 ,
то ,
то  | |
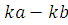 , ,  | |
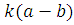 , но тогда условие , но тогда условие 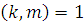 дает дает  | |
 , т.е. , т.е.  . .
Теорема 7
. Если  и и 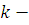 произвольное натуральное число, то произвольное натуральное число, то 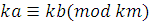 . .
Доказательство
. Если 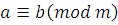 , то , то  | |
 , ,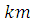 | |
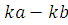 , ,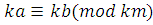 . .
Теорема 8
. Если 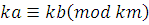 , где , где 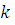 и и 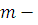 произвольные натуральные числа, то произвольные натуральные числа, то . .
Доказательство
. Если 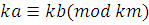 , то , то 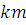 | |
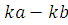 , , 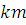 | |
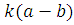 , ,
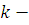 натуральное ( натуральное (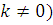 , тогда , тогда  | |
 , ,
 . .
Теорема 9
. Если  , ,
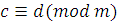 , то , то 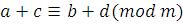 и и 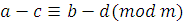 . .
Доказательство
. Если  и и 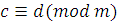 ,
то ,
то 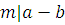 и и 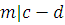 . Получим, что . Получим, что 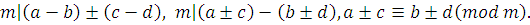
Теорема 9'
. Если  ,
то ,
то 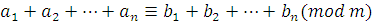 . .
Теорема 10
. Если  и и
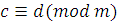 , то , то 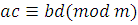 . .
Доказательство
. Если  и и 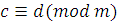 , то , то 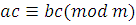 и и 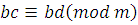 . Тогда по транзитивности сравнений получим, что . Тогда по транзитивности сравнений получим, что 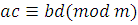 . .
Теорема 10'
. Если  , то , то
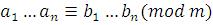 . .
Доказательство
. Последовательно применяя теорему 7, получим:
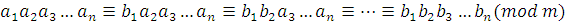 . .
Теорема 11
. Если  , то при любом целом , то при любом целом 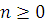 , ,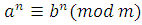 . .
Доказательство
. При 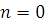 утверждение верно по теореме 2, а при утверждение верно по теореме 2, а при 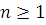 оно верно согласно теореме 10', если оно верно согласно теореме 10', если 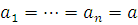 и и 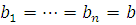 . .
Переход от сравнений  , ,
 к сравнениям к сравнениям
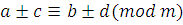 , ,
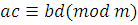 , ,
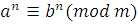
будем называть соответственно сложением (вычитанием), умножением, возведением в степень сравнений.
Так как из сравнения  следует следует  , то из сравнений , то из сравнений  и и  следует также, что следует также, что 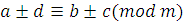 и и  . .
Теорема 12
. Если  и и 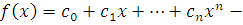 произвольный многочлен с целыми коэффициентами, то произвольный многочлен с целыми коэффициентами, то 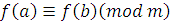 . .
Доказательство
. Если  , то, согласно теоремам 7 и 11, имеем: , то, согласно теоремам 7 и 11, имеем:
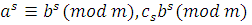 при при 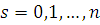 . .
По теореме 9', получаем 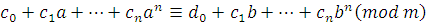 , ,
т.е. 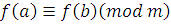 . .
Теорема 12'
. Если 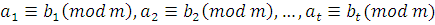 и и 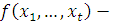 многочлен с целыми коэффициентами, то многочлен с целыми коэффициентами, то
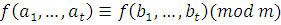 . .
Теорема 13
. Любое слагаемое левой или правой части сравнения можно перенести с противоположным знаком в другую часть.
Доказательство
. Ввиду симметричности отношения сравнения достаточно рассмотреть случай, когда дано сравнение 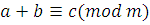 .
Складывая это сравнение со сравнением .
Складывая это сравнение со сравнением 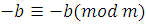 ,
получаем ,
получаем 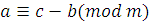 . .
Сервис онлайн-записи на собственном Telegram-боте
Попробуйте сервис онлайн-записи VisitTime на основе вашего собственного Telegram-бота:
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно.
Зарегистрироваться в сервисе
Следствие
. В левой и правой частях сравнения можно добавлять или отбрасывать одно и то же слагаемое.
Теорема 14
. В сравнении можно отбрасывать или добавлять слагаемые, делящиеся на модуль.
Доказательство
. Если 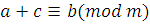 и и 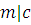 , т.е. , т.е.  , то, складывая эти сравнения, получаем , то, складывая эти сравнения, получаем  . Аналогично из . Аналогично из  и и 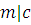 получаем получаем 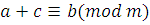 . .
Поскольку левую и правую части сравнения можно менять местами, утверждение верно и для слагаемых правой части.
Теорема 15
. Если и и 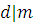 , то , то  . .
Доказательство
. Если  , то , то 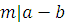 . Из . Из 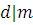 , ,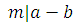 в силу транзитивности отношения делимости получаем в силу транзитивности отношения делимости получаем 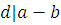 , ,
 . .
Теорема 16
.
Если  , то множество общих делителей , то множество общих делителей 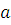 и и 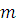 совпадает с множеством общих делителей совпадает с множеством общих делителей 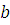 и и 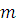 . В частности, . В частности, 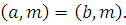
Доказательство
. Если  , то , то 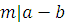 , , 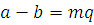 , , 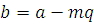 , любой общий делитель , любой общий делитель 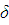 чисел чисел 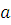 и и 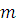 является общим делителем чисел является общим делителем чисел 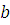 и и 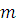 , и, наоборот, если , и, наоборот, если 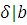 и и 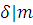 , то , то 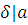 . .
Поскольку пара 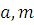 и пара и пара 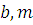 имеют одни и те же общие делители, то и имеют одни и те же общие делители, то и 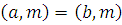 . .
Теорема 17
. Если 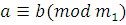 , ,
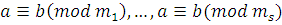 , то , то  , где , где 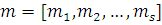 . .
Доказательство
. Если 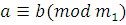 , ,
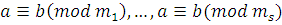 , то , то  , то , то  и, согласно свойствам наименьшего общего кратного, и, согласно свойствам наименьшего общего кратного,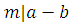 . .
2. Сравнения первой степени с одной переменной
2.1 Основные понятия
Определение
1
. Сравнением первой степени с одной переменной называется сравнение вида
| 
|
(2.1)
|
где 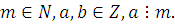
Будем говорить, что целое число 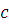 удовлетворяет сравнению (2.1), если удовлетворяет сравнению (2.1), если  верное сравнение. верное сравнение.
Теорема
1
. Если целое число 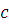 удовлетворяет сравнению (*), то и весь класс удовлетворяет сравнению (*), то и весь класс 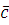 по по 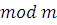 состоит из чисел, удовлетворяющих этому сравнению. состоит из чисел, удовлетворяющих этому сравнению.
Доказательство
. Имеем: 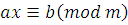 , отсюда получим, что , отсюда получим, что 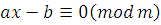 . Обозначим через . Обозначим через 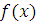 разность разность 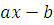 , то есть , то есть 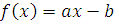 . Следовательно, . Следовательно,  . А так как число . А так как число 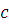 удовлетворяет сравнению (2.1), то сравнение удовлетворяет сравнению (2.1), то сравнение
| 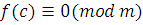
|
(2.2)
|
является верным. Кроме того, 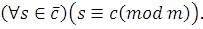
Получим
| 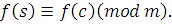
|
(2.3)
|
Но тогда по свойству транзитивности из (2.2) и (2.3) получим, что
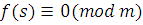 , ,
то есть 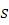 удовлетворяет сравнению (2.1), поэтому весь класс удовлетворяет сравнению (2.1), поэтому весь класс 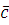 , состоит из чисел, удовлетворяющих сравнению (2.1). Теорема 1 доказана. , состоит из чисел, удовлетворяющих сравнению (2.1). Теорема 1 доказана.
Определение 2
. Решением сравнения (2.1) называется класс вычетов по 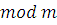 , которые при подстановке в сравнение обращают его в верное сравнение. , которые при подстановке в сравнение обращают его в верное сравнение.
Число решений сравнения по 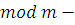 это число решений этого сравнения в какой-либо полной системе вычетов по модулю это число решений этого сравнения в какой-либо полной системе вычетов по модулю 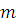 . .
Примеры.
1) 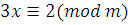 . Полная система наименьших неотрицательных вычетов по модулю 7: . Полная система наименьших неотрицательных вычетов по модулю 7: 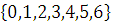 (так как классы вычетов будут (так как классы вычетов будут 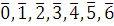 ). ).
Если 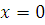 , то , то 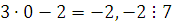 , следовательно, , следовательно, 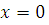 не удовлетворяет сравнению. не удовлетворяет сравнению.
Если 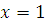 , то , то 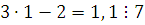 , следовательно, , следовательно, 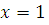 не удовлетворяет сравнению. не удовлетворяет сравнению.
Если 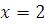 , то , то 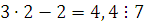 , следовательно, , следовательно, 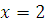 не удовлетворяет сравнению. не удовлетворяет сравнению.
Если 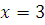 , то , то 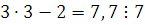 , следовательно, , следовательно, 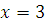 удовлетворяет сравнению, а поэтому класс вычетов удовлетворяет сравнению, а поэтому класс вычетов 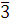 по по 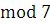 является решением сравнения. является решением сравнения.
Если 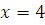 , то , то 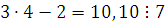 , следовательно, , следовательно, 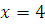 не удовлетворяет сравнению. не удовлетворяет сравнению.
Если 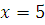 , то , то 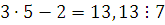 , следовательно, , следовательно, 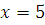 не удовлетворяет сравнению. не удовлетворяет сравнению.
Если 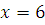 , то , то 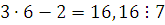 , следовательно, , следовательно, 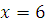 не удовлетворяет сравнению. не удовлетворяет сравнению.
Таким образом, сравнение имеет одно решение 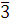 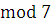 или, в другом виде, или, в другом виде, 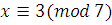 . .
Ответ: 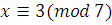 . .
2)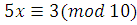 . .
Классы вычетов по mod 10: 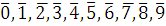 . Полная система наименьших по абсолютной величине вычетов по mod 10: {0, 1, 2, 3, 4, 5, -4, -3, -2, -1}. Проверим для каждого из этих чисел, будет ли выполнено условие . Полная система наименьших по абсолютной величине вычетов по mod 10: {0, 1, 2, 3, 4, 5, -4, -3, -2, -1}. Проверим для каждого из этих чисел, будет ли выполнено условие 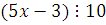 . Имеем: . Имеем:
Получили, что ни одно из чисел, взятых из полной системы вычетов, не удовлетворяет сравнению, следовательно, данное сравнение не имеет решения.
Ответ: 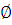 . .
Теорема 1
.
Пусть дано сравнение
| 
|
(2.4)
|
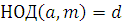 , , 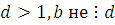 . Тогда сравнение (2.4) не имеет решения. . Тогда сравнение (2.4) не имеет решения.
Доказательство
. От противного. Предположим, что существует решение: класс вычетов 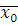 по mod m. Тогда по mod m. Тогда 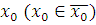 удовлетворяет сравнению, то есть удовлетворяет сравнению, то есть 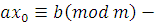 верное сравнение. Отсюда получим, что верное сравнение. Отсюда получим, что
| 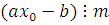
|
(2.5)
|
Из условия теоремы: 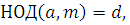 следует, что следует, что
| 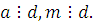
|
(2.6)
|
Поэтому из (2.5) и (2.6) получим, что 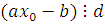 и и 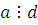 , отсюда следует, что , отсюда следует, что 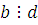 . Получили противоречие: . Получили противоречие: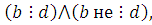 так как сделали неправильное предположение. Отбросив его, получим, что сравнение (2.4) не имеет решения. Теорема 1 доказана. так как сделали неправильное предположение. Отбросив его, получим, что сравнение (2.4) не имеет решения. Теорема 1 доказана.
Рассмотрим сравнение:
| 
|
(2.7)
|
где 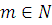 , , 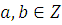 , , 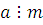 . Если . Если 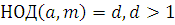 и и 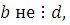 то сравнение не имеет решения. то сравнение не имеет решения.
Пусть теперь 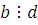 , тогда будем иметь: , тогда будем иметь: 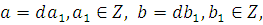
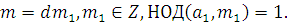
Поэтому получим: 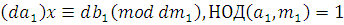 . Так как по определению НОД число . Так как по определению НОД число 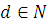 , то из последнего сравнения получим: , то из последнего сравнения получим:
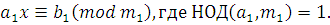
Таким образом, полагая в (1), что НОД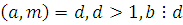 , мы пришли к сравнению такого же вида, но с условием: , мы пришли к сравнению такого же вида, но с условием: 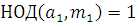 . Исследуем этот случай. . Исследуем этот случай.
Теорема 1
.
Пусть дано сравнение (2.7) и НОД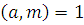 . Тогда сравнение (2.7) имеет единственное решение. . Тогда сравнение (2.7) имеет единственное решение.
Доказательство.
Так как НОД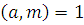 , то класс вычетов , то класс вычетов 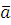 по mod m принадлежит мультипликативной группе классов вычетов, взаимно простых с mod m. Поэтому (по свойству группы) уравнение по mod m принадлежит мультипликативной группе классов вычетов, взаимно простых с mod m. Поэтому (по свойству группы) уравнение 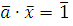 имеет единственное решение имеет единственное решение 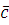 , где , где 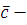 класс вычетов по mod m, взаимно простых с m. Значит, для класс вычетов по mod m, взаимно простых с m. Значит, для 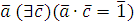 , но тогда , но тогда 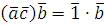 , отсюда , отсюда 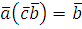 . Обозначим через . Обозначим через 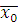 класс вычетов класс вычетов 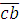 no mod m, тогда получим, что для no mod m, тогда получим, что для 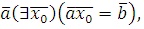 следовательно, следовательно,  , a , a 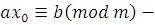 верное сравнение, то есть класс верное сравнение, то есть класс 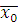 является решением сравнения (2.7). Это решение единственно, так как существует единственный класс является решением сравнения (2.7). Это решение единственно, так как существует единственный класс 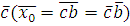 . Теорема 1 доказана. . Теорема 1 доказана.
Пример 1
. 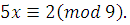 НОД (5,9) = 1, следовательно, сравнение имеет одно решение. Найдем его способом «подбора», то есть перебирая все числа из полной системы вычетов по mod
m
: {0, 1, 2, 3, 4, 5, б, 7, 8} (m
= 9
). НОД (5,9) = 1, следовательно, сравнение имеет одно решение. Найдем его способом «подбора», то есть перебирая все числа из полной системы вычетов по mod
m
: {0, 1, 2, 3, 4, 5, б, 7, 8} (m
= 9
).
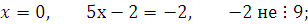
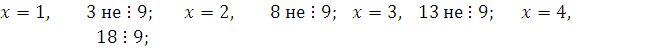
следовательно, 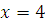 удовлетворяет сравнению, поэтому решением будет класс вычетов удовлетворяет сравнению, поэтому решением будет класс вычетов 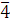 по mod
m
или, по-другому, по mod
m
или, по-другому,  . .
А так как данное сравнение имеет 1 решение, то остальные числа 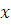 : 5, 6, 7, 8 проверять уже не надо. : 5, 6, 7, 8 проверять уже не надо.
Ответ:  . .
Заметим, что для нахождения решения сравнения первой степени с одной переменной (если оно есть) существует несколько способов:
1) подбора;
2) преобразования коэффициентов;
3) Эйлера (с помощью функции Эйлера);
4) цепных дробей.
Если модуль m является простым числом, то есть  , число , число 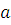 не делится на не делится на 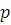 , то сравнение имеет единственное решение. Следовательно, множество классов вычетов , то сравнение имеет единственное решение. Следовательно, множество классов вычетов 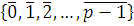 образует поле по отношению сложения и умножения классов вычетов. Его обозначают через образует поле по отношению сложения и умножения классов вычетов. Его обозначают через 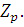
Пример 2
. Вычислить остаток при делении 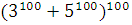 на 15. на 15.
Решение
. 1 способ.
Сравнение 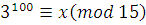 для применения теоремы Эйлера сократим на 3 (очевидно, для применения теоремы Эйлера сократим на 3 (очевидно, 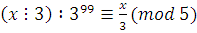 . .
Так как 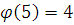 , то по теореме Ферма показатель 99 можно уменьшить по модулю 4. Получаем, что из , то по теореме Ферма показатель 99 можно уменьшить по модулю 4. Получаем, что из 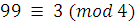 следует: следует:
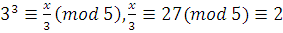 . .
Умножаем на 3 обе части сравнения и модуль: 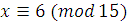 , т.е. , т.е.
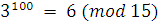 . .
Аналогично вычисляем 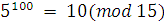 . Отсюда почленным сложением сравнений найдем: . Отсюда почленным сложением сравнений найдем: 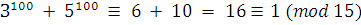 . Затем, возводя в 100-ю степень обе части сравнения, получаем . Затем, возводя в 100-ю степень обе части сравнения, получаем 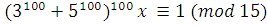 . .
Ответ: 1.
2 способ.
Сравнение 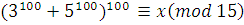 рассмотрим отдельно по модулям 3 и 5 (делители 15). Так как рассмотрим отдельно по модулям 3 и 5 (делители 15). Так как 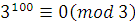 и и 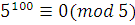 , то , то
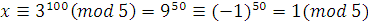 , ,
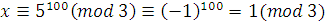 . .
Среди целых чисел от 0 до 14 (возможные остатки при делении на 15) только 1, 6, 11 сравнимы с 1 по модулю 5. А среди этих трех только 1 сравнима с 1 по модулю 3, т.е. 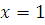 .
Тогда .
Тогда 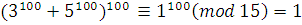 . .
3 способ.
Число 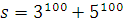 не делится на 3 (первое слагаемое делится, а второе не делится) и не делится на 5. Так как 3 и 5 есть простые числа, то не делится на 3 (первое слагаемое делится, а второе не делится) и не делится на 5. Так как 3 и 5 есть простые числа, то 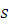 с ними взаимно просто и взаимно просто с 15. По теореме Эйлера с ними взаимно просто и взаимно просто с 15. По теореме Эйлера
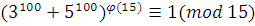 , , 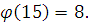
Ответ: 1.
Пример 3
. Разложить 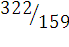 в цепную дробь. Проверить разложение, свернув цепную дробь последовательным вычислением подходящих дробей. в цепную дробь. Проверить разложение, свернув цепную дробь последовательным вычислением подходящих дробей.
Решение
. Найдём элементы цепной дроби как частные в алгоритме Евклида:
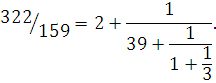
Сделаем сокращённую запись: 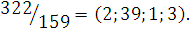
Пусть 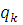 обозначает обозначает 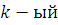 элемент цепной дроби, элемент цепной дроби, 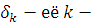 ю подходящую дробь, ю подходящую дробь, 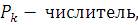 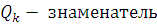 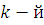 подходящей дроби. Будем вычислять подходящие дроби по рекуррентной формуле подходящей дроби. Будем вычислять подходящие дроби по рекуррентной формуле
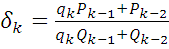 , ,
используя схему:
| 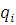
|
2
|
39
|
1
|
3
|
| 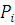
|
1
|
2
|
79
|
81
|
322
|
| 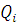
|
0
|
1
|
39
|
40
|
159
|
Как видно, последняя подходящая дробь совпадает с исходным числом.
Замечание. Непосредственное сворачивание конечной цепной дроби «снизу вверх» обычно громоздко:
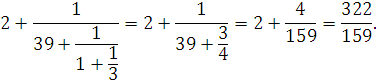
Задачи для самостоятельного решения
.
Задача 1
. Сократите дробь 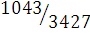 , применяя алгоритм Евклида. , применяя алгоритм Евклида.
Задача 2
. Сколько натуральных чисел взаимно просто с 520 и не превосходит это число? (решить с помощью функции Эйлера)
Задача 3
. Решить сравнение 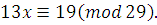
Задача 4
. Найти все целочисленные решения уравнения 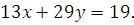
Теорема
1
. Пусть дано сравнение:
| 
|
(2.8)
|
НОД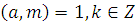 и и 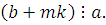 Тогда класс вычетов Тогда класс вычетов 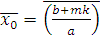 по модулю m
является решением сравнения (2.8). по модулю m
является решением сравнения (2.8).
Доказательство
. Так как НОД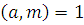 , то сравнение , то сравнение  имеет одно решение. Кроме того, имеет одно решение. Кроме того, 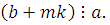 Возьмем целое число Возьмем целое число 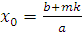 , , 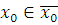 , тогда , тогда 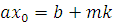 , следовательно, получим сравнение: , следовательно, получим сравнение: 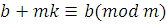 , которое является верным сравнением. , которое является верным сравнением.
Поэтому целое число 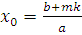 удовлетворяет сравнению, а, значит, класс вычетов удовлетворяет сравнению, а, значит, класс вычетов 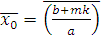 по модулю m
является решением сравнения. Теорема 1 доказана. по модулю m
является решением сравнения. Теорема 1 доказана.
Примеры.
1) 
НОД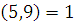 , поэтому сравнение имеет единственное решение. , поэтому сравнение имеет единственное решение.
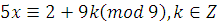 . .
Найдем такое целое число k
, чтобы 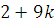 делилось на 5. Например, делилось на 5. Например, 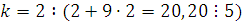 . Тогда получим: . Тогда получим: 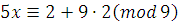 , , 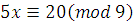 . .
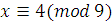
Проверка. 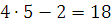 , 18 делится на 9, поэтому при подстановке в сравнение вместо переменной значения 4, получим верное сравнение, следовательно, число 4 удовлетворяет сравнению, поэтому класс целых чисел, содержащий число 4, является решением сравнения. , 18 делится на 9, поэтому при подстановке в сравнение вместо переменной значения 4, получим верное сравнение, следовательно, число 4 удовлетворяет сравнению, поэтому класс целых чисел, содержащий число 4, является решением сравнения.
Ответ: 
2) 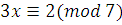
НОД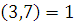 , следовательно, сравнение имеет одно решение. , следовательно, сравнение имеет одно решение.
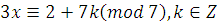 (при (при 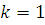 будет будет 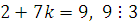 ) )
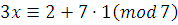 , , 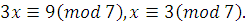
Ответ:  . .
Получим метод решения сравнения
| 
|
(2.9)
|
с помощью функции Эйлера.
Теорема 1
.
Пусть дано сравнение (2.9), 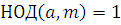 . Тогда класс вычетов . Тогда класс вычетов
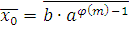
по модулю m
является решением сравнения (2.9), где 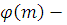 функция Эйлера. функция Эйлера.
Доказательство
. Так как 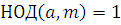 , то по теореме Эйлера имеет место сравнение , то по теореме Эйлера имеет место сравнение 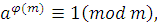 где где 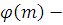 функция Эйлера функция Эйлера
Выберем 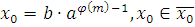 , тогда при подстановке его вместо , тогда при подстановке его вместо 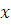 в сравнение (2.9) и, учитывая, что в сравнение (2.9) и, учитывая, что
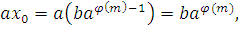
получим сравнение
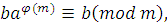
которое является верным в силу теоремы Эйлера. Следовательно,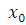 удовлетворяет сравнению (2.9), а класс вычетов удовлетворяет сравнению (2.9), а класс вычетов
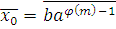
по модулю m
является решением сравнения, или, по-другому, 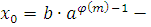 решение сравнения (2.9). Теорема 1 доказана. решение сравнения (2.9). Теорема 1 доказана.
Примеры.
1) 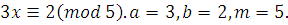
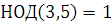 , следовательно, сравнение имеет одно решение, , следовательно, сравнение имеет одно решение, 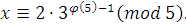
Преобразуем произведение 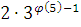 . . 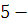 простое число, то простое число, то 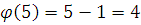 . Поэтому . Поэтому 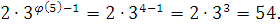
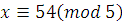 , , 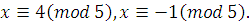
Ответ: 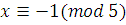 . .
2)  . .
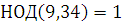 , поэтому сравнение имеет одно решение. , поэтому сравнение имеет одно решение.
1-й способ – способ подбора. Полная система наименьших по абсолютной величине вычетов по модулю 34: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 25, 26, 27, 28, 29, 30, 31, 32, 33}.
Проверим, какое из этих чисел 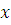 удовлетворяет сравнению, то есть удовлетворяет сравнению, то есть 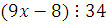 . Это будет . Это будет 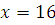 , так как , так как 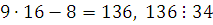 . Следовательно, . Следовательно,  решение сравнения. решение сравнения.
Ответ:  . .
2-й способ – способ преобразования коэффициентов.
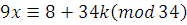 , k , k
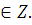
Найдем такое целое число 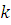 , при котором , при котором 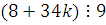 . Например, . Например, 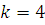 , тогда , тогда 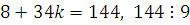 . .
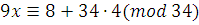 , ,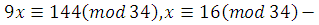 решение сравнения. решение сравнения.
Ответ: 
3-й способ – метод Эйлера (с помощью функции Эйлера).
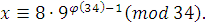
Упростим произведение 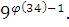
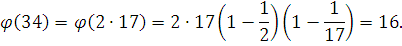
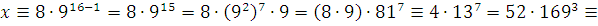
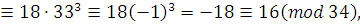
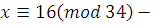 решение сравнения. решение сравнения.
Ответ: 
3. Сравнения высших степеней
3.1 Основные понятия
Определение 1.
Сравнением n
-й степени с одной переменной называется сравнение вида
| 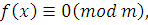
|
(3.1)
|
где 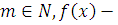 многочлен с целыми коэффициентами: многочлен с целыми коэффициентами:
| 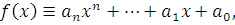
|
(3.2)
|
причем, 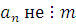 . .
Целое число 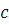 удовлетворяет сравнению (3.1), если сравнение удовлетворяет сравнению (3.1), если сравнение 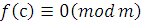 является верным сравнением. является верным сравнением.
Теорема 1
. Пусть дано сравнение (3.1) и целое число 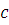 удовлетворяет сравнению (3.1). Тогда весь класс удовлетворяет сравнению (3.1). Тогда весь класс 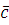 по mod m
состоит из чисел, удовлетворяющих сравнению (3.1). по mod m
состоит из чисел, удовлетворяющих сравнению (3.1).
Доказательство
. Число 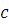 удовлетворяет сравнению (3.1), следовательно, удовлетворяет сравнению (3.1), следовательно, 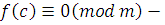 верное сравнение. Для любого верное сравнение. Для любого 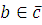 всегда всегда  . Но тогда по свойству сравнений . Но тогда по свойству сравнений 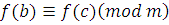 , поэтому по транзитивности получим, что , поэтому по транзитивности получим, что 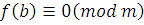 , отсюда следует, что число , отсюда следует, что число 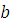 удовлетворяет сравнению (3.1). А так как удовлетворяет сравнению (3.1). А так как 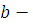 произвольное из произвольное из 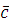 , то, следовательно, весь класс вычетов , то, следовательно, весь класс вычетов 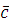 по mod m
состоит из чисел, удовлетворяющих сравнению (3.1). Теорема 1 доказана. по mod m
состоит из чисел, удовлетворяющих сравнению (3.1). Теорема 1 доказана.
Определение 2.
Решением сравнения (3.1) называется класс вычетов по модулю m
, состоящий из чисел, удовлетворяющих сравнению (3.1).
Если класс 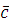 mod m
является решением сравнения (3.1), то будем говорить, что класс mod m
является решением сравнения (3.1), то будем говорить, что класс 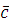 удовлетворяет сравнению (3.1). Числом решений сравнения (3.1) называется число классов вычетов по mod m
, удовлетворяющих сравнению (3.1). удовлетворяет сравнению (3.1). Числом решений сравнения (3.1) называется число классов вычетов по mod m
, удовлетворяющих сравнению (3.1).
Задача нахождения чисел, удовлетворяющих сравнению (3.1), сводится к нахождению классов, удовлетворяющих уравнению 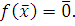
Действительно:
· так как 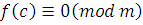 верно, то верно, то 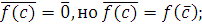
· обратно, если 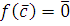 , то , то 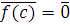 , следовательно, , следовательно, 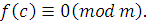
Чтобы решить сравнение 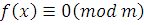 , можно , можно
1) взять любую полную систему вычетов по mod m
:
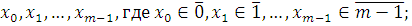
2) вычислить 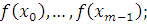
3) взять те числа 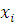 , при которых сравнение , при которых сравнение 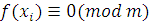 является верным, то есть является верным, то есть 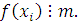 Соответствующие классы Соответствующие классы 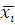 , дадут все решения сравнения. , дадут все решения сравнения.
Удобнее брать полную систему наименьших по абсолютной величине вычетов по mod  . Если сравнение имеет несколько решений . Если сравнение имеет несколько решений 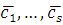 , то эти решения можно записывать в виде , то эти решения можно записывать в виде 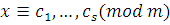 (то есть (то есть 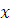 принимает любые значения, сравнимые с одним из чисел принимает любые значения, сравнимые с одним из чисел 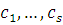 ) вместо записи ) вместо записи 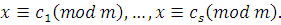
Примеры.
1) 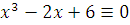 (mod 11). (mod 11).
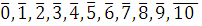 классы вычетов по mod 11. классы вычетов по mod 11.
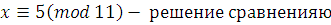
2) 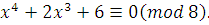
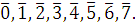 Сравнение не имеет решения. Сравнение не имеет решения.
3)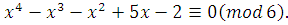

Ответ: 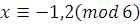
Задача нахождения решения сравнения 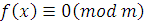 проще, чем рассматриваемая в курсе алгебры задача нахождения решения уравнения проще, чем рассматриваемая в курсе алгебры задача нахождения решения уравнения  . Так как решая уравнение в некотором бесконечном множестве (R, С) нельзя перебрать все числа . Так как решая уравнение в некотором бесконечном множестве (R, С) нельзя перебрать все числа 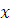 . А решая сравнение . А решая сравнение 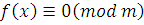 , ищем решение в конечном кольце Zm
классов вычетов по mod m
. Следовательно, с помощью конечного числа операций можно найти все решения. Но надо заметить, что при больших m
будут громоздкие вычисления, поэтому надо изучить способы, позволяющие определить число решений, а иногда и способы нахождения решения с помощью возможно меньшего числа операций. , ищем решение в конечном кольце Zm
классов вычетов по mod m
. Следовательно, с помощью конечного числа операций можно найти все решения. Но надо заметить, что при больших m
будут громоздкие вычисления, поэтому надо изучить способы, позволяющие определить число решений, а иногда и способы нахождения решения с помощью возможно меньшего числа операций.
Рассмотрим сравнение с одной переменной вида
| 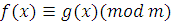
|
(3.3)
|
где 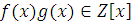 , , 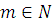 , коэффициенты при старшем члене , коэффициенты при старшем члене 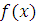 и и 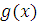 не делятся на m. не делятся на m.
Определение 1.
Решением сравнения (3.3) называется класс вычетов по mod
m
, состоящий из чисел, удовлетворяющих этому сравнению.
Теорема 1.
Пусть 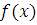 и и 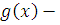 многочлены с целыми коэффициентами и целое число многочлены с целыми коэффициентами и целое число 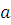 удовлетворяет сравнению (3.3). Тогда весь класс вычетов удовлетворяет сравнению (3.3). Тогда весь класс вычетов 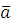 (mod
m
)
состоит из чисел, удовлетворяющих этому сравнению. (mod
m
)
состоит из чисел, удовлетворяющих этому сравнению.
Доказательство.
1) Так как число 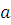 удовлетворяет сравнению (3.3), то оно удовлетворяет сравнению удовлетворяет сравнению (3.3), то оно удовлетворяет сравнению 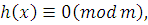 , где , где 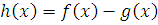 . .
2) 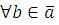 mod m будет mod m будет  , следовательно, , следовательно, 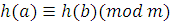 , поэтому число , поэтому число 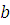 удовлетворяет сравнению удовлетворяет сравнению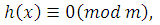 то есть сравнению то есть сравнению 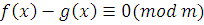 . Следовательно, число . Следовательно, число 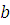 удовлетворяет сравнению (3.3). Таким образом, класс вычетов удовлетворяет сравнению (3.3). Таким образом, класс вычетов 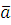 состоит из чисел, удовлетворяющих сравнению (3.3). Теорема 1 доказана. состоит из чисел, удовлетворяющих сравнению (3.3). Теорема 1 доказана.
Определение
2
. Два сравнения
| 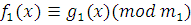
|
(3.4)
|
и
| 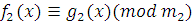
|
(3.5)
|
называются эквивалентными, если множество чисел, удовлетворяющих одному из них, совпадает с множеством чисел, удовлетворяющих другому сравнению.
Если 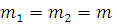 и сравнения (3.4) и (3.5) имеют одни и те же решения, то получим два эквивалентных сравнения по и сравнения (3.4) и (3.5) имеют одни и те же решения, то получим два эквивалентных сравнения по 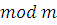 . .
Эквивалентные сравнения могут иметь разную степень.
Пример.
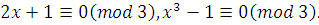
Решение первого сравнения: 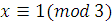 , решением второго сравнения тоже будет класс вычетов , решением второго сравнения тоже будет класс вычетов 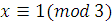 . Следовательно, они эквивалентны. Но степени их различны (степень первого сравнения равна 1, степень второго – 3). . Следовательно, они эквивалентны. Но степени их различны (степень первого сравнения равна 1, степень второго – 3).
Теорема 1.
Пусть дано сравнение
| 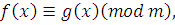
|
(3.6)
|
где 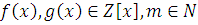 . .
Тогда имеют место следующие утверждения:
1) Если к обеим частям сравнения (3.6) прибавить любой многочлен 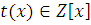 то получится сравнение, эквивалентное сравнению (3.6). то получится сравнение, эквивалентное сравнению (3.6).
2) Если обе части сравнения (3.6) умножить на одно и то же целое число, взаимно простое с модулем, то получится сравнение, эквивалентное сравнению (3.6).
3) Если обе части сравнения и модуль умножить на одно и то же натуральное число 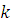 , то получится сравнение, эквивалентное сравнению (3.6). , то получится сравнение, эквивалентное сравнению (3.6).
Доказательство.
1) Пусть класс вычетов 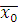 но модулю но модулю 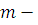 решение сравнения (3.6), то есть для решение сравнения (3.6), то есть для 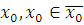 сравнение сравнение
2)
| 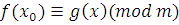
|
(3.7)
|
является верным сравнением, следовательно, сравнение
| 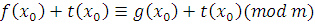 , ,
|
(3.8)
|
где 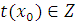 , тоже верно. Поэтому класс вычетов , тоже верно. Поэтому класс вычетов 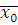 по модулю по модулю  является решением сравнения является решением сравнения
| 
|
(3.9)
|
Обратное также верно: если 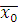 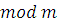 решение сравнения (3.9), то для решение сравнения (3.9), то для 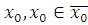 , будет верно сравнение (3.8), а, следовательно, верно сравнение (3.7), поэтому , будет верно сравнение (3.8), а, следовательно, верно сравнение (3.7), поэтому 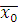 является решением сравнения (3.6). является решением сравнения (3.6).
Таким образом, сравнения (3.6) и (3.9) эквивалентны.
3) Пусть класс вычетов 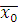 по по 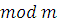 – решение сравнения (3.6), тогда для – решение сравнения (3.6), тогда для 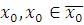 , получим верное сравнение , получим верное сравнение 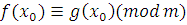 . Возьмем целое число . Возьмем целое число 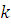 , взаимно простое с модулем: , взаимно простое с модулем: 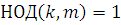 . Умножим последнее сравнение почленно на . Умножим последнее сравнение почленно на 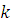 , получим верное сравнение: , получим верное сравнение:
| 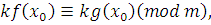
|
(3.10)
|
отсюда получим, что класс вычетов 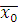 по модулю по модулю 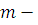 решение сравнения решение сравнения
| 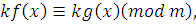
|
(3.11)
|
Обратно, если класс вычетов 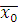 по модулю по модулю 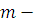 решение сравнения (3.11), то для решение сравнения (3.11), то для 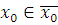 верно сравнение (3.10), следовательно, будет верно и сравнение: верно сравнение (3.10), следовательно, будет верно и сравнение:
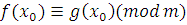
(заметим, что 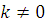 , так как , так как 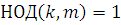 , в противном случае было бы: , в противном случае было бы: 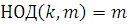 ). Поэтому класс вычетов ). Поэтому класс вычетов 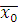 по модулю по модулю 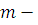 решение сравнения (3.6). решение сравнения (3.6).
Таким образом, сравнения (3.6) и (3.11), где 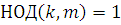 , будут эквивалентными. , будут эквивалентными.
3) Пусть класс вычетов 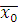 по модулю по модулю 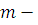 решение сравнения (3.6), тогда для решение сравнения (3.6), тогда для 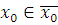 верно сравнение верно сравнение 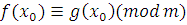 , а, значит, верно и сравнение , а, значит, верно и сравнение
4)
| 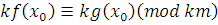
|
(3.12)
|
для любого натурального числа 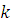 , поэтому класс вычетов , поэтому класс вычетов 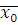 по модулю по модулю 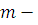 решение сравнения решение сравнения
| 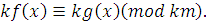
|
(3.13)
|
Обратно, если класс вычетов 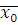 по модулю по модулю 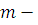 решение сравнения (3.13), то для решение сравнения (3.13), то для 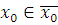 верно сравнение (3.12), но тогда по свойству сравнений верно сравнение: верно сравнение (3.12), но тогда по свойству сравнений верно сравнение: 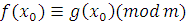 , поэтому класс вычетов , поэтому класс вычетов 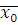 по модулю по модулю 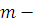 решение сравнения (3.6). Следовательно, сравнения (3.6) и (3.13) эквивалентны. Теорема доказана. решение сравнения (3.6). Следовательно, сравнения (3.6) и (3.13) эквивалентны. Теорема доказана.
В дальнейшем сравнение (3.6) можно заменить эквивалентным сравнением:
| 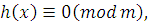
|
(3.14)
|
где 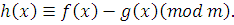 Теорема 1 доказана. Теорема 1 доказана.
Теорема 2.
Пусть даны сравнения 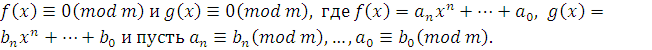 Тогда сравнения эквивалентны. Тогда сравнения эквивалентны.
Доказательство
. Умножим почленно верные сравнения на 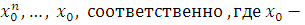 некоторое целое число: некоторое целое число:
Сложим почленно полученные сравнения, тогда получим сравнение:
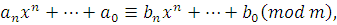
отсюда получим, что 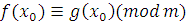 . Но тогда . Но тогда 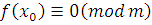 и и 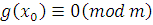 . Следовательно, сравнения . Следовательно, сравнения 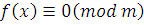 и и 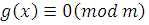 эквивалентны. Теорема 2 доказана. эквивалентны. Теорема 2 доказана.
Заметим, из доказанной теоремы, в частности, следует, что сравнение заменится эквивалентным, если отбросить (или добавить) слагаемое с коэффициентами, делящимися на модуль.
Переходя от сравнений 1-й степени к сравнениям более высоких степеней, целесообразно сначала рассмотреть тот случай, когда модуль – простое число. В этом случае имеется ряд весьма важных теорем, которые, вообще говоря, неверны для составных модулей. Вместе с тем теория сравнений по простому модулю является основой, на которой строится изучение сравнений по составному модулю.
Во всей этой главе буквой 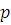 будем обозначать модуль, представляющий собой простое число. будем обозначать модуль, представляющий собой простое число.
Теорема 1.
Если 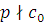 , то сравнение , то сравнение
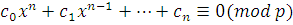
может быть заменено эквивалентным сравнением с коэффициентом при старшем члене, равном единице.
Доказательство.
Рассмотрим сравнение 1-й степени 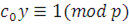 ; поскольку ; поскольку 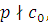 то и сравнение имеет решение. Найдем число то и сравнение имеет решение. Найдем число 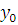 , удовлетворяющее этому сравнению, т.е. , удовлетворяющее этому сравнению, т.е. 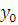 такое, что такое, что 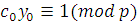 . .
Тогда сравнение 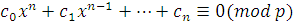 эквивалентно сравнению эквивалентно сравнению
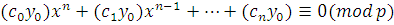 , ,
а следовательно, сравнению
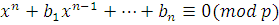 , ,
где 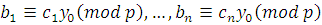 . .
Пример 1.
Заменить сравнение
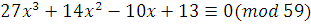
эквивалентным сравнением с коэффициентом при старшем члене, равным 1.
Решаем сравнение 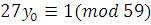 и находим и находим 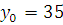 . Данное нам сравнение эквивалентно сравнению . Данное нам сравнение эквивалентно сравнению
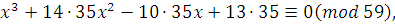
т.е. сравнению 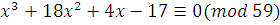 . .
Теорема 2.
Если 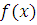 и и 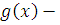 многочлены с целыми коэффициентами, то сравнения по простому модулю многочлены с целыми коэффициентами, то сравнения по простому модулю
| 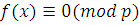
|
(3.15)
|
| 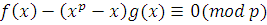
|
(3.16)
|
эквивалентны.
Доказательство.
Пусть 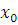 удовлетворяет сравнению (3,15), т.е. удовлетворяет сравнению (3,15), т.е. 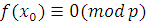 . Поскольку при любом . Поскольку при любом 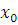 согласно теореме Ферма согласно теореме Ферма 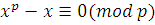 , то , то
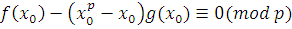 . .
Пользуясь той же теоремой Ферма, получаем, что если 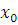 удовлетворяет сравнению (3,16), то удовлетворяет сравнению (3,16), то 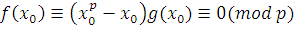 ,
и, таким образом, сравнения (3,15) и (3,16) эквивалентны. ,
и, таким образом, сравнения (3,15) и (3,16) эквивалентны.
Из этой теоремы непосредственно вытекает следующая.
Теорема 3.
Сравнение по простому модулю 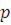 , степень которого больше, чем этот модуль или равна ему, может быть заменено эквивалентным сравнением степени, меньшей , степень которого больше, чем этот модуль или равна ему, может быть заменено эквивалентным сравнением степени, меньшей 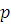 . .
Доказательство.
Пусть 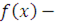 многочлен с целыми коэффициентами степени многочлен с целыми коэффициентами степени 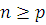 . При делении . При делении 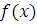 на на 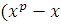 ), частное ), частное 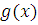 и остаток и остаток 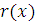 будут также многочленами с целыми коэффициентами: будут также многочленами с целыми коэффициентами:
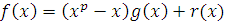 , ,
где степень 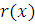 меньше степени меньше степени 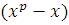 , т.е. меньше, чем , т.е. меньше, чем 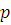 . Согласно предыдущей теореме, сравнения . Согласно предыдущей теореме, сравнения 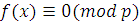 и и 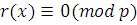 эквивалентны. эквивалентны.
Пример 2.
Сравнение 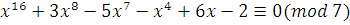 заменить эквивалентным сравнением степени, меньшей чем 7. заменить эквивалентным сравнением степени, меньшей чем 7.
Решение.
Мы получим эквивалентное сравнение, если заменим 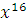 на на 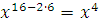 , , 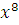 на на 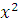 , , 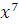 на на 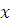 . Таким образом, заданное сравнение эквивалентно сравнению . Таким образом, заданное сравнение эквивалентно сравнению
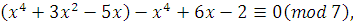
т.е. сравнению 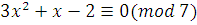 . .
Теорема 4.
Если 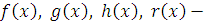 многочлены с целыми коэффициентами: многочлены с целыми коэффициентами: 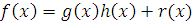 , и все коэффициенты , и все коэффициенты 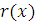 делятся на простое число делятся на простое число 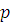 , то любое решение сравнения , то любое решение сравнения
| 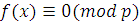
|
(3.17)
|
является решением, по крайней мере, одного из сравнений:
| 
|
(3.18)
|
Доказательство.
Пусть 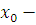 решение сравнения (3.17), т.е. решение сравнения (3.17), т.е. 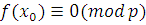 . Поскольку все коэффициенты . Поскольку все коэффициенты 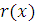 делятся на делятся на 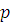 , будем также иметь , будем также иметь 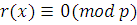 , поэтому , поэтому
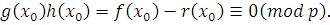
Из сравнимости произведения 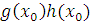 с нулем по модулю с нулем по модулю 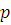 следует, что по крайней мере один из этих множителей сравним с нулем по этому модулю, т.е. следует, что по крайней мере один из этих множителей сравним с нулем по этому модулю, т.е. 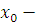 решение по крайней мере одного из сравнений (3.18). решение по крайней мере одного из сравнений (3.18).
Пример 3.
В сравнении 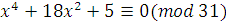 левую часть можно представить в виде левую часть можно представить в виде  , и мы находим все решения этого сравнения, решая сравнения: , и мы находим все решения этого сравнения, решая сравнения:  , , 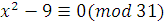 , т.е. , т.е.  и и 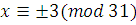 . Все эти четыре класса удовлетворяют нашему сравнению. . Все эти четыре класса удовлетворяют нашему сравнению.
Для составных модулей эта теорема неверна. Например, сравнению
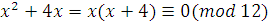
удовлетворяет класс 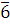 , не являющийся решением ни одного из сравнений: , не являющийся решением ни одного из сравнений:
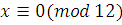 , , 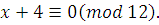
Теорема 5.
Сравнение степени 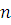 по простому модулю по простому модулю 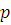 с коэффициентом при старшем члене, не делящимся на с коэффициентом при старшем члене, не делящимся на 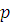 , может иметь не больше чем , может иметь не больше чем 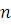 решений. решений.
Доказательство.
Утверждение теоремы верно при 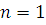 . Действительно, в этом случае мы имеем сравнение 1-й степени: . Действительно, в этом случае мы имеем сравнение 1-й степени: 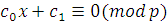 , где , где 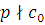 , т.е. , т.е. 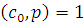 , а такое сравнение имеет в точности одно решение. Применим теперь для доказательства теоремы метод полной математической индукции. , а такое сравнение имеет в точности одно решение. Применим теперь для доказательства теоремы метод полной математической индукции.
Предположим, что утверждение теоремы верно для всех многочленов (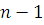 ) – й степени со старшими коэффициентами, не делящимися на простой модуль ) – й степени со старшими коэффициентами, не делящимися на простой модуль 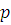 . Возьмем теперь произвольный многочлен – й степени: . Возьмем теперь произвольный многочлен – й степени:
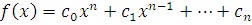 , ,
где 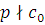 , и рассмотрим сравнение , и рассмотрим сравнение
| 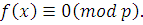
|
(3.19)
|
Если это сравнение не имеет ни одного решения, то число решений меньше чем 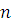 . .
Если же это сравнение имеет решения, то возьмем любое число 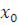 , удовлетворяющее ему, и разделим , удовлетворяющее ему, и разделим 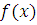 на на 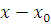 . Согласно теореме Безу будем иметь: . Согласно теореме Безу будем иметь:
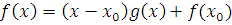 . .
Коэффициенты многочлена 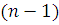 -й степени -й степени 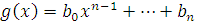 могут быть найдены по схеме Горнера и представляют собой целые числа, причем могут быть найдены по схеме Горнера и представляют собой целые числа, причем 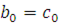 . .
Поскольку 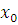 удовлетворяет сравнению (3.19), удовлетворяет сравнению (3.19), 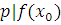 , то все решения (3,19) находятся среди решений сравнений , то все решения (3,19) находятся среди решений сравнений 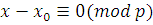 и и 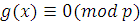 , удовлетворяя либо одному из них, либо обоим. , удовлетворяя либо одному из них, либо обоим.
Сравнение 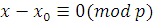 имеет одно решение, а сравнение имеет одно решение, а сравнение 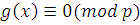 представляет собой сравнение ( представляет собой сравнение (
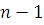 ) –
й степени по простому модулю с коэффициентом при старшем члене ) –
й степени по простому модулю с коэффициентом при старшем члене 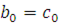 ,
не делящемся на ,
не делящемся на 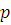 , и, по предположению, может иметь не больше чем , и, по предположению, может иметь не больше чем 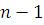 решений. Таким образом, сравнение (5) имеет не больше, чем решений. Таким образом, сравнение (5) имеет не больше, чем 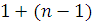 , т.е. не больше чем , т.е. не больше чем 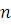 решений. решений.
Согласно принципу математической индукции справедливость теоремы доказана.
Пример 4.
 удовлетворяет сравнению удовлетворяет сравнению  Найти все решения этого сравнения. Найти все решения этого сравнения.
Очевидно, что вместе с классом 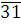 этому сравнению удовлетворяет и класс этому сравнению удовлетворяет и класс 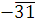 . Коэффициент при старшем члене . Коэффициент при старшем члене 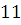 не делится на простой модуль не делится на простой модуль 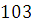 , поэтому сравнение не может иметь больше двух решений. , поэтому сравнение не может иметь больше двух решений.
Ответ
. 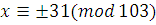 . .
Для составных модулей эта теорема неверна. Сравнение степени 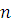 по составному модулю с коэффициентом при старшем члене, не делящемся на модуль или даже взаимно простом с модулем, может иметь больше чем по составному модулю с коэффициентом при старшем члене, не делящемся на модуль или даже взаимно простом с модулем, может иметь больше чем 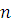 решений. Например, сравнение решений. Например, сравнение 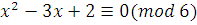 имеет 4 решения: имеет 4 решения: 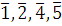 . .
Теорема 6.
Если сравнение степени 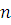 по простому модулю по простому модулю 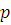 имеет больше чем имеет больше чем 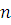 решений, то все коэффициенты сравнения делятся на решений, то все коэффициенты сравнения делятся на 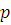 . .
Доказательство.
Возьмем любое простое число 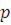 . Если сравнение . Если сравнение 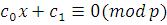 имеет больше чем одно решение, то имеет больше чем одно решение, то 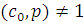 , т.е. , т.е. 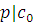 . Таким образом, при . Таким образом, при 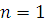 теорема верна. Предположим, что утверждение теоремы верно для многочленов степени, меньшей чем теорема верна. Предположим, что утверждение теоремы верно для многочленов степени, меньшей чем 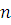 , т.е. предположим, что число решений сравнения степени, меньшей чем , т.е. предположим, что число решений сравнения степени, меньшей чем 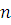 , может превосходить степень сравнения только тогда, когда все коэффициенты делятся на модуль , может превосходить степень сравнения только тогда, когда все коэффициенты делятся на модуль 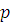 . .
Возьмем любое сравнение степени 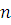 : :
| 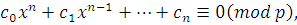
|
(3.20)
|
имеющее больше чем 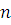 решений. В таком сравнении решений. В таком сравнении 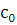 делится на делится на 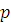 , а тогда сравнение , а тогда сравнение
| 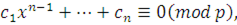
|
(3.21)
|
эквивалентное сравнению (3.20), также имеет больше чем 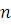 решений. решений.
В сравнении (3.21), степень которого меньше чем 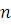 , а число решений превосходит степень согласно предположению, все коэффициенты должны делиться на , а число решений превосходит степень согласно предположению, все коэффициенты должны делиться на 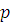 , т.е. , т.е. 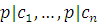 . Поскольку уже раньше было установлено, что . Поскольку уже раньше было установлено, что 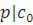 , утверждение теоремы верно для , утверждение теоремы верно для 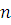 . Согласно принципу математической индукции справедливость теоремы доказана. . Согласно принципу математической индукции справедливость теоремы доказана.
Теорема 7.
Пусть  многочлен с целыми коэффициентами и свободным членом многочлен с целыми коэффициентами и свободным членом  , где , где 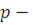 простое число, причем простое число, причем 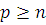 . Сравнение . Сравнение 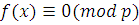 имеет имеет 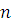 решений тогда и только тогда, когда все коэффициенты остатка от деления решений тогда и только тогда, когда все коэффициенты остатка от деления 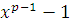 на на 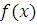 кратны кратны 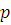 . .
Доказательство.
Пусть 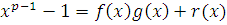 , где , где 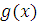 и и 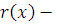 многочлены с целыми коэффициентами, причем степень многочлены с целыми коэффициентами, причем степень 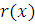 меньше чем меньше чем 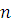 . .
1) Докажем достаточность условия. Пусть коэффициенты 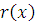 делятся на делятся на 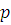 . .
Обозначим через  и и  соответственно число решений сравнений соответственно число решений сравнений
| 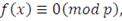
|
(3.22)
|
| 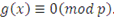
|
(3.23)
|
Сравнение 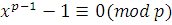 по теореме Ферма имеет по теореме Ферма имеет 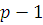 решений. Каждое из этих решений. Каждое из этих 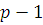 решений является решением хотя бы одного из сравнений: (3.22) или (3.23), т.е. решений является решением хотя бы одного из сравнений: (3.22) или (3.23), т.е. 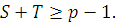
Сравнение (3.23) степени 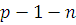 имеет коэффициент при старшем члене, равный единице, так что имеет коэффициент при старшем члене, равный единице, так что 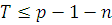 и, следовательно, и, следовательно,
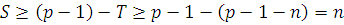 . .
Поскольку при этом 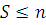 , получаем , получаем 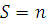 , т.е. из делимости коэффициентов , т.е. из делимости коэффициентов 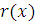 на на 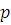 следует, что число решений сравнения (3.22) равно следует, что число решений сравнения (3.22) равно 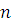 . .
2) Докажем необходимость условия. Пусть сравнение (3.22) имеет 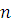 решений. Если решений. Если 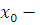 решение сравнения (3.22), то решение сравнения (3.22), то 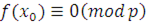 и вместе с тем, поскольку и вместе с тем, поскольку 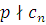 , то , то 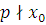 , а, следовательно, согласно теореме Ферма, , а, следовательно, согласно теореме Ферма, 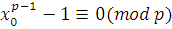 , так что , так что
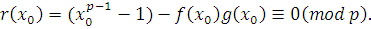
Таким образом, каждое из 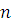 решений сравнения (3.22) является решением сравнения решений сравнения (3.22) является решением сравнения 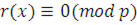 , степень которого меньше чем , степень которого меньше чем 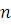 . Следовательно, все коэффициенты . Следовательно, все коэффициенты 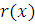 делятся на делятся на 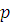 . .
Пример 5.
Сравнению  удовлетворяют классы удовлетворяют классы 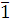 и и 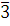 . Имеет ли это сравнение еще одно решение? . Имеет ли это сравнение еще одно решение?
Делим 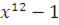 на на 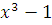 , находим: , находим: 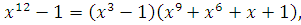
так что 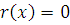 и, следовательно, это сравнение имеет три решения. и, следовательно, это сравнение имеет три решения.
Некоторые из рассмотренных нами теорем можно легко обобщить на случай сравнений с несколькими неизвестными вида:
| 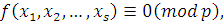
|
(3.24)
|
где 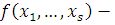 многочлен с целыми коэффициентами, а многочлен с целыми коэффициентами, а  простое число. простое число.
Теорема 1.
Если в левой части сравнения (3.24) некоторые из неизвестных встречаются в виде степени с показателем 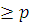 , то сравнение (3.24) можно заменить эквивалентным сравнением, в котором степень каждого из неизвестных не превосходит , то сравнение (3.24) можно заменить эквивалентным сравнением, в котором степень каждого из неизвестных не превосходит 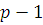 . .
Доказательство.
Сравнение (3.24) эквивалентно сравнению

где  произвольный многочлен с целыми коэффициентами. произвольный многочлен с целыми коэффициентами.
Если среди слагаемых 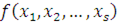 есть член вида есть член вида
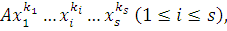
где 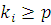 , то мы можем, взяв , то мы можем, взяв
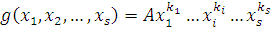 , ,
заменить его членом 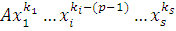 , затем , затем 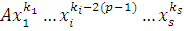 и т.д. и т.д.
Если 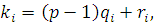 где где 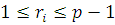 , то в показателе для , то в показателе для 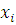 можно отбросить можно отбросить 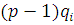 и получить эквивалентное сравнение, в котором слагаемое и получить эквивалентное сравнение, в котором слагаемое 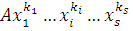 будет заменено на будет заменено на 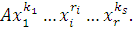 Проделав такие операции для всех слагаемых по отношению к каждому из неизвестных, входящему с показателем Проделав такие операции для всех слагаемых по отношению к каждому из неизвестных, входящему с показателем 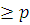 , получим сравнение, эквивалентное первоначальному, в котором степень по отношению к каждому неизвестному будет не больше чем , получим сравнение, эквивалентное первоначальному, в котором степень по отношению к каждому неизвестному будет не больше чем 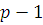 . .
Теорема 2.
Если сравнение 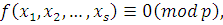 степень которого по каждому неизвестному меньше чем степень которого по каждому неизвестному меньше чем 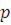 , удовлетворяется при всех целых , удовлетворяется при всех целых 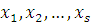 , то все коэффициенты многочлена , то все коэффициенты многочлена 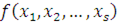 делятся на делятся на 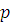 . .
Доказательство.
Проведем индукцию по числу неизвестных 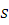 . При . При 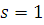 утверждение теоремы верно. Предположим, что утверждение теоремы верно при утверждение теоремы верно. Предположим, что утверждение теоремы верно при 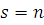 , и возьмем произвольное тождественное сравнение , и возьмем произвольное тождественное сравнение 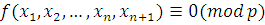 , степень которого по каждому неизвестному меньше чем , степень которого по каждому неизвестному меньше чем 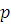 . Если . Если 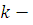 наибольший показатель степени неизвестного наибольший показатель степени неизвестного 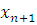 , то сравнение можно представить в виде: , то сравнение можно представить в виде:
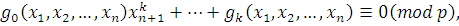
где все 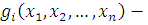 многочлены с целыми коэффициентами, степени которых по каждому неизвестному меньше чем многочлены с целыми коэффициентами, степени которых по каждому неизвестному меньше чем 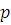 . Если вместо . Если вместо 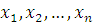 подставить любые целые числа, то получим тождественное сравнение с неизвестной подставить любые целые числа, то получим тождественное сравнение с неизвестной 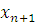 степени степени 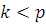 . Все коэффициенты этого сравнения: . Все коэффициенты этого сравнения: 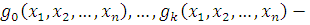 должны при любых значениях должны при любых значениях 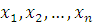 делиться на делиться на 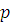 . Поскольку согласно предположению для многочленов от . Поскольку согласно предположению для многочленов от 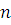 аргументов утверждение теоремы верно, все коэффициенты этих многочленов, а следовательно, и многочлена аргументов утверждение теоремы верно, все коэффициенты этих многочленов, а следовательно, и многочлена 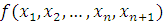 должны делиться на должны делиться на 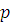 . .
Согласно принципу полной математической индукции утверждение теоремы верно для любого числа аргументов.
4.1 Системы сравнений первой степени
Систему сравнений первой степени с одним и тем же неизвестным, но с разными модулями, запишем в общем виде так:
| 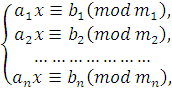
|
(4.1)
|
|
Общий способ (способ последовательного решения) состоит в том, что сначала находится 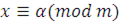 из первого сравнения, где из первого сравнения, где 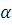 – наименьший неотрицательный или абсолютно наименьший вычет по модулю – наименьший неотрицательный или абсолютно наименьший вычет по модулю 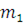 и берется класс чисел и берется класс чисел
| 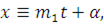
|
(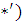
|
удовлетворяющих первому сравнению.
Затем это значение 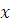 подставляется во второе сравнение, что дает подставляется во второе сравнение, что дает
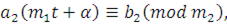
откуда находится 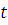 опять в виде класса чисел и подставляется в равенство ( опять в виде класса чисел и подставляется в равенство (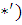 . .
В результате получается значение 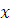 в виде класса чисел, удовлетворяющих первым двум сравнениям системы. Дальше это значение в виде класса чисел, удовлетворяющих первым двум сравнениям системы. Дальше это значение 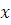 подставляется в третье сравнение системы, так же находится подставляется в третье сравнение системы, так же находится 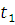 , затем находится , затем находится 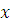 и подставляется в четвертое сравнение системы и т.д. и подставляется в четвертое сравнение системы и т.д.
Заметим, что можно идти и несколько иным путем: сначала решается каждое из сравнений системы и представляется в виде:
| 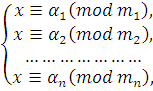
|
(4.2)
|
а затем поступают описанным способом.
Если окажется, что хотя бы одно из сравнений системы (4.1) не имеет решения или сравнение относительно 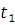 в описанном способе неразрешимо, то система (4.1) не имеет решения. в описанном способе неразрешимо, то система (4.1) не имеет решения.
Если для сравнений 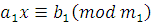 системы (4.1) системы (4.1) 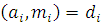 и и 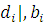 то, сокращая члены и модуль каждого сравнения на то, сокращая члены и модуль каждого сравнения на 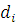 получаем систему: получаем систему:
| 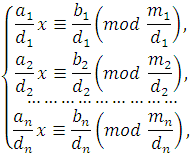
|
(4.3)
|
эквивалентную (4.1).
Сравнения этой системы можно решить относительно 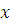 и свести решение системы (4.3) к решению системы: и свести решение системы (4.3) к решению системы:
| 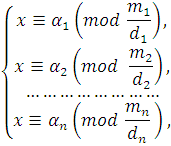
|
(4.4)
|
Если в системе (4.2) модули 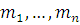 попарно просты, то решение ее можно находить не указанным выше общим способом, а по формуле: попарно просты, то решение ее можно находить не указанным выше общим способом, а по формуле:
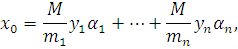
где 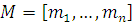 и и 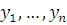 есть решения сравнений: есть решения сравнений:
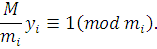
Решением системы будет: 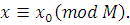
Этим способом можно решать и систему (4.4), если модули 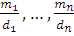 попарно просты. попарно просты.
Пример
1
.
Решить систему сравнений:
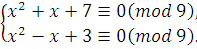
Классы вычетов по 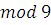 : : 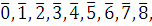 при при 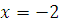 имеем: имеем:
1) 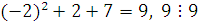 , следовательно, , следовательно, 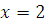 удовлетворяет первому сравнению системы, удовлетворяет первому сравнению системы,
2) 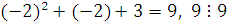 , следовательно, , следовательно, 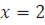 удовлетворяет второму сравнению системы. удовлетворяет второму сравнению системы.
Поэтому класс вычетов 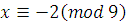 является решением системы. Можно записать этот класс иначе: прибавив к является решением системы. Можно записать этот класс иначе: прибавив к 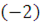 модуль 9, получим, что модуль 9, получим, что 
Итак, данная система сравнений имеет решение 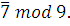
В работе изложены основы теории сравнений. Задача данной курсовой работы разработка учебного пособия, которое содержит достаточный теоретический и практический материал.
В данной работе достаточно полно изложены основные моменты теории, они иллюстрируются примерами, которые позволяют глубже понять рассматриваемые вопросы.
Материал курсовой работы может быть использован как при изучении соответствующего курса теории чисел, так и для спецкурсов по алгебре, в частности, для тех специальностей, на которых нет курса теории чисел, уже на младших курсах обучения.
Приведенный список литературы позволяет при необходимости рассмотреть некоторые более сложные моменты теории сравнений и их приложений.
Литература
1. Бухштаб А.А. Теория чисел. – М.: Просвещение, 1960. – 376 с.
2. Алгебра и теория чисел: Уч. пособие. под ред. Н.Я. Виленкина. – М.: Просвещение, 1984. – 192 с. (гл. 3).
3. Вахитова Е.В. Теория сравнений и ее приложения. – Стерлитамак: Изд-во СГПИ, 2000. – 414 с.
4. Фаддеев Д.К., Соминский И.С. Сборник задач по высшей алгебре. – М.: Наука, 1984. – 288 с.
5. Лельчук М.П., Полевченко И.И., Радьков А.М., Чеботаревский Б.Д. Практические занятия по алгебре и теории чисел. – Минск: Высш. Школа, 1986. – 302 с. (Занятия 46–51).
6. Шнеперман Л.Б. Сборник задач по алгебре и теории чисел. – Мн.: Высш. шк., – 1982. – 223 с.
7. Михелович Ш.Х. Теория чисел. М.: Высшая Школа, 1967. – 335 с.
8. Грибанов П.И., Титов П.И. Сборник упражнений по теории чисел. М. Просвещение 1964.
9. Александров В.А., Горшенин С.М. Задачник-практикум по теории чисел. М.: Просвещение 1960. – 48 с.
|