Министерство
образования
и науки
Республики
Казахстан
Карагандинский
Металлургический
институт
Факультет
экономики и
строительства
Кафедра
Экономической
теории
КОНТРОЛЬНАЯ
РАБОТА № 1
ТЕМА:
Сводка и группировка
Подготовил
студент
группы Э-04с
Омаров
А.К.
Проверила
ст.
преподаватель
Артыкбаева
А.А.
Темиртау
– 2005
СПИСОК
ИСПОЛЬЗОВАННОЙ
ЛИТЕРАТУРЫ:
Переяслова
И.Г. Статистика,
серия Высшее
образование.
– Ростов на
Дону: “Феникс”,
2003 – 288 с.
Кильдишев
Г.С. Общая теория
статистики,
М.: Статистика,
1980 г. – 423 с.
Математический
энциклопедический
словарь. М.: Наука,
1922 г.
Лабораторная
работа № 1
Тема
Сводка и группировка
Карточка
Исходные
данные
Имеются
следующие
данные о средне
– дневной заработной
плате 100 рабочих
цеха
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
1
|
2,4
|
3,1
|
3,6
|
4
|
4,1
|
4,4
|
4,9
|
5,3
|
5,6
|
6,1
|
|
2
|
2,5
|
3,1
|
3,6
|
4
|
4,1
|
4,5
|
4,9
|
5,3
|
5,7
|
6,2
|
|
3
|
2,6
|
3,2
|
3,7
|
4
|
4,1
|
4,5
|
4,9
|
5,3
|
5,7
|
6,2
|
|
4
|
2,7
|
3,3
|
3,7
|
4
|
4,2
|
4,5
|
5
|
5,4
|
5,8
|
6,3
|
|
5
|
2,7
|
3,3
|
3,7
|
4
|
4,2
|
4,5
|
5
|
5,4
|
5,8
|
6,3
|
|
6
|
2,8
|
3,4
|
3,7
|
4
|
4,3
|
4,6
|
5
|
5,4
|
5,9
|
6,4
|
|
7
|
2,9
|
3,4
|
3,7
|
4
|
4,4
|
4,6
|
5
|
5,5
|
5,9
|
6,5
|
|
8
|
2,9
|
3,5
|
3,8
|
4,1
|
4,4
|
4,7
|
5,1
|
5,5
|
5,9
|
6,6
|
|
9
|
2,9
|
3,6
|
3,8
|
4,1
|
4,4
|
4,7
|
5,2
|
5,5
|
6
|
6,8
|
|
10
|
3
|
3,6
|
4
|
4,1
|
4,4
|
4,7
|
5,2
|
5,5
|
6,1
|
7,4
|
Задание:
Построить
интервальный
ряд распределения,
объединив
материал в 8
групп
Вычислить с
точностью до
0,1 среднюю
арифметическую,
моду, медиану,
средне – квадратичное
отклонение,
коэффициент
вариации
Изобразить
полученный
ряд графически
при помощи
полигона и
гистограммы
частот (построить
2 графика отдельно)
Определить
размах вариации,
квартильное
отклонение,
коэффициент
осцилляции,
коэффициент
линейного
отклонения
- Определить
корреляционное
отношение
Решение
1. Построение
интервального
ряда
Для построения
интервального
ряда необходимо
определить
шаг интервала
(i)
I = (Xmax-
Xmin)/ N
Xmax, Xmin
– максимальное
и минимальное
значение совокупности
N – Количество
образуемых
интервалов
I = (7,4
– 5,4) / 8
= 0,625
|
№ ряда
|
Интервал ряда
|
Частота
ряда
|
|
1
|
2,4
– 3,025
|
10
|
|
2
|
3,025
– 3,65
|
12
|
|
3
|
3,65
– 4,275
|
23
|
|
4
|
4,275
– 4,9
|
15
|
|
5
|
4,9
– 5,525
|
20
|
|
6
|
5,525
– 6,15
|
11
|
|
7
|
6,15
– 6,775
|
7
|
|
8
|
6,775
– 7,4
|
2
|
|
ИТОГО:
|
100
|
- Вычислить
Среднюю
арифметическую
Моду
Медиану
Средне
– квадратичное
отклонение
- Коэффициент
вариации
a) Расчет
средней арифметической
Средняя
арифметическая
в вариационных
рядах рассчитывается
как средняя
арифметическая
взвешенная
по формуле
Х (средняя) = Е
Х f / Е
f,
где
Х средняя
арифметическая
I - го
интервала
f частота
ряда
Расчет
средней арифметической
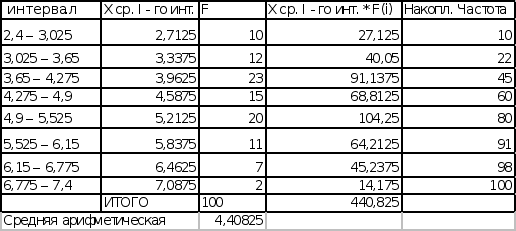
b) Расчет
Моды
Mo =
Xo +
I * (fmo -
fmo-1)/(
(fmo
- fmo-1)
+ (fmo
- fmo+1)),
где
Xo
– нижняя
граница модального
интервала
I – величина
интервала
fmo
– частота
модального
интервала
fmo-1
- частота
домодального
интервала
fmo+1
– частота
постмодального
интервала
Мода
– интервал с
большим числом
признаков
Mo
= 3,65 + 0,625 * (23-12)/((23-12)+(23-15)) = 4,01 тенге
c) Расчет
медианы
Mе = Xме
+ I *(((Е
f/2) –
Sme
-1)/ Fme)
где
Xme
– нижняя
граница медианного
интервала
(интервала, для
которого накопленная
совокупность
впервые превысит
полусумму
частот всей
совокупности
I – величина
интервала
Sme
-1 сумма накопленных
частот предмедианного
интервала
Е
f/2 - полусумма
частот всей
совокупности
Mе =
4,275+0.625*((50-45)/15)=4,5 тенге
d)
Расчет среднеквадратичного
отклонения
G (X)
= D (X)^0.5;
D(X)
= M (X^2)
– M(X)^2,
где
G(X) - средне-
квадратическое
отклонение
D (X)
– Дисперсия
M(X)
– Математическое
ожидание (Средняя
величина по
всей совокупности)
M (X^2)
= Е
Х^2*f
РАСЧЕТ M
(X^2)
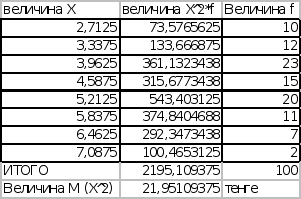
D (X)
= 21,9 – (4,4) ^2= 2,5 тенге
G (X)
= 2,5 ^0.5 = 1,6 тенге
e)
Коэффициент
вариации
V = G(x)
/ x (средняя)
V = (1,6/4,4)*100% = 36 %
Вывод
– совокупность
не однородна
3.
ГРАФИЧЕСКАЯ
ИНТЕРПРЕТАЦИЯ
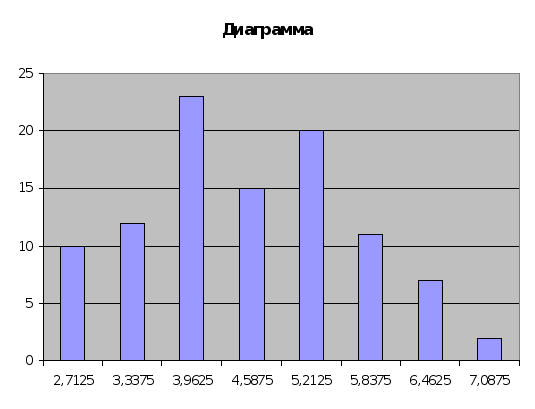
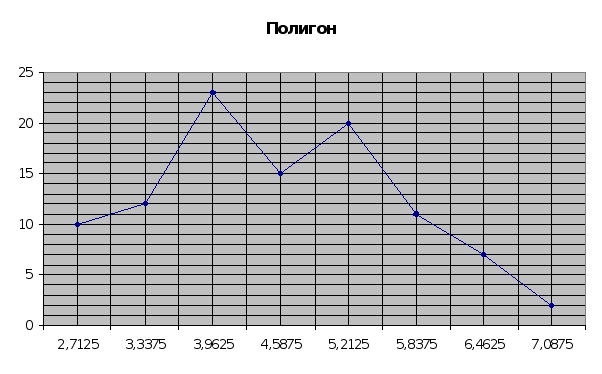
4. Определить
размах
вариации,
квартильное
отклонение,
коэффициент
осцилляции,
- коэффициент
линейного
отклонения
a) Размах
вариации
Размах вариации
представляет
собой разницу
между максимальным
и минимальным
значением
R = X max – X min
R = 7,4 – 5,4 = 2 тенге
b)
Квартильное
отклонение
Квартильное
отклонение
- разница между
3 – ей и 1 –ой квартилями
деленное на
2
Расчет первой
квартили:
Q1
= XQ1+I
* (1/4 E
F – SQ1-1)/
f Q1
XQ1
– нижняя часть
интервала
содержащего
первую квартиль
I – величина
интервала
1/4 E
F –
четверть признаков
всей совокупности
SQ1-1
– накопленная
частота интервала,
находящегося
перед первой
квартилью
Q1
= 3,65+0,625*(25-22)/23 = 3,7 тенге
Расчет третьей
квартили:
Q3
= XQ3+I
* (3/4 E
F – SQ3-1)/
f Q3
XQ3
– нижняя часть
интервала
содержащего
третью квартиль
I – величина
интервала
3/4 E
F – 75 %
признаков всей
совокупности
SQ3-1
– накопленная
частота интервала,
находящегося
перед третьей
квартилью
Q3
=4,9+0,625*(75-60)/20=5,4 тенге
Qоткл.=
(Q3-Q1)/2
Qоткл.=
(5,4 -3,7)/2=0.85 тенге
c)
Коэффициент
осцилляции
Косц..= R/X
(средняя)
R – Размах
вариации
X (средняя)
– средняя
арифметическая
по всей совокупности
Косц..= 2/4,4 =
0,45(45 %)
d)
Коэффициент
линейного
отклонения
Кd =
d / X (средняя)*100%
d – линейное
отклонение
X (средняя)
– средняя
арифметическая
по всей совокупности
d = (E
(X - X
(средняя))*f)/F
X – среднее
значение I – го
интервала
X (средняя)
– средняя
арифметическая
по всей совокупности
f – Частота
I --го интервала
F – Количество
признаков всей
совокупности
Расчет
коэффициента
линейного
отклонения
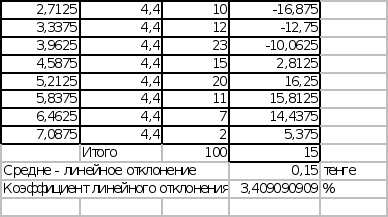
5.
Эмпирическое
корреляционное
отношение
J2 = S
2 (x)
/ G2 (x)
– доля межгрупповой
дисперсии в
общей
S
2 (x)
– Межгрупповая
дисперсия
G2 (x)
– Общая дисперсия
S
2 (x)
= (E
(X - X
(средняя))
2*f)/F
– межгрупповая
дисперсия
G2 (х) =
S
2 (x)
+ G2 (х)
(средняя из
групповых
дисперсий)
G2 (х)
(средняя из
групповых
дисперсий) = (E
G2i*f)/F
G2i
– внутригрупповая
дисперсия I
– го ряда
Разобьем
совокупность
на два ряда и
по каждому
найдем среднюю
арифметическую
и дисперсию
Первый
ряд

Второй
ряд

Средняя
из групповых
дисперсий
G2 (х)
(средняя из
групповых
дисперсий) =
0,4*0,6+0,3*0,4= 0,36
Межгрупповая
дисперсия
S
2 (x)
= (4,4-3,8)^2* 0,6 + (4,4-5,7)^2 *0.4 = 0,9
Коэффициент
детерминации
J2 =0,9/(0,36+0,9)=0,71
Эмпирическое
корреляционное
отношение
характеризует
тесноту связи
J = (J2)1/2
J = 0, 71^0,
5 = 0,84 |