| Содержание
Введение………………………………………………………………………..……………………………………3
1 Теоретическая часть. 4
1.1 Основные понятия теории графов. 4
1.2 Порядок и правила построения сетевых графиков. 6
1.3 Нахождение максимального потока в сети. 13
2 Практическая часть. 20
2.1 Задача о нефтепроводе максимальной пропускной способности. 20
Выводы и рекомендации……………………………………………………………...………….24
Библиографический список……………………………………………………………….….25
Введение
Современное общество отчасти можно рассматривать как систему сетей, предназначенных для транспортирования, передачи и распределения электроэнергии, товаров и информации. Для решения задач оптимального использования этих систем применяется сетевой анализ. В значительной степени он основан на теории графов. Сетевые модели широко применяются в исследовании операций и могут быть использованы на практике, например, при проектировании вычислительных комплексов, транспортных сетей, телетрансляционных сетей, систем космической связи.
Ни один проект с использованием крупной сети со сложной топологией в настоящее время не обходится без исчерпывающего моделирования будущей сети. Программы, выполняющие эту задачу, достаточно сложны и дороги. Целью моделирования является определение оптимальной топологии, адекватный выбор сетевого оборудования, определение рабочих характеристик сети и возможных этапов будущего развития. Ведь сеть, слишком точно оптимизированная для решений задач текущего момента, может потребовать серьезных переделок в будущем. Так, в данной курсовой работе будут рассмотрены основные модели теории графов, и методы решения сетевых задач на примере задачи о нефтепроводе.
Сетевой моделью (другие названия: сетевой график, сеть) называется экономико-компьютерная модель, отражающая комплекс работ (операций) и событий, связанных с реализацией некоторого проекта (научно-исследовательского, производственного и др.), в их логической и технологической последовательности и связи. Анализ сетевой модели, представленной в графической или табличной (матричной) форме, позволяет более четко выявить взаимосвязи этапов реализации проекта, а также определить наиболее оптимальный порядок выполнения этих этапов в целях, например, сокращения сроков выполнения всего комплекса работ. Таким образом, методы сетевого моделирования относятся к методам принятия оптимальных решений.
Реклама

Графом называется набор точек, соединенных между собой ребрами (или дугами).
Таким образом, ребро определяется парой вершин. Два ребра, у которых есть общая вершина, называются смежными (или соседними).
Граф называется ориентированным (или орграфом), если некоторые ребра имеют направление. Это означает, что в орграфе некоторая вершина может быть соединена с другой вершиной, а обратного соединения нет. Геометрически граф часто изображают точками плоскости, причем соседние вершины соединены дугами (для орграфа некоторые дуги имеют направление, что обычно отмечают стрелкой).
Помимо этого, в теории графов рассматриваются также мультиграфы – это такие графы, в которых могут быть петли (т. е. некоторая вершина соединена сама с собой ребром) или некоторые пары вершины могут быть соединены между собой несколькими ребрами.
Маршрут в графе – это последовательность соседних (смежных) вершин. Ясно, что можно определить маршрут и как последовательность смежных ребер (в этом случае ребра приобретают направление). Заметим, что в маршруте могут повторяться вершины, но не ребра. Маршрут называется циклом, если в нем первая вершина совпадает с последней.
Путь в графе (иногда говорят простой путь) – это маршрут без повторения вершин (а значит, и ребер).
Контур – это цикл без повторения вершин, за исключением первой вершины, совпадающей с последней.
Последовательности вершин (рис. 1): 1–2–3–4–2–5 не простой путь, а маршрут; последовательности 1–2–3–4–7–5 и 1–2–5 – простые пути; 1–2–3–4–2–5–6–1 –это цикл (но не контур); 1–2–5–6–1 – это контур. Если имеется некоторый маршрут из вершины t в вершину s, заданный в виде последовательности ребер, которые в этом случае приобрели направление, и если в этот маршрут входит ребро, соединяющее вершины (i, j), то это ребро по отношению к вершине i называют иногда прямой дугой, а по отношению к вершине j – обратной дугой (или обратным ребром).
Граф называется связным, если любые две его вершины можно соединить маршрутом (или путем). На рис. 1 изображен связный граф.
Ребро, при удалении которого граф перестает быть связным, иногда называют мостом или перешейком.
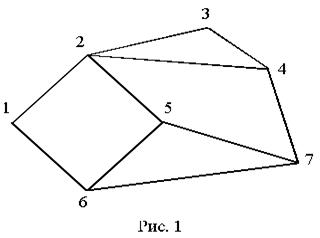
Рисунок 1 – Связный граф
Степень вершины – это число ребер, входящих в эту вершину. Вершина называется висячей, если ее степень равна единице.
Лемма 1. Если степень всех вершин в графе больше или равна двум, то граф обязательно содержит контур.
Реклама

Доказательство. Действительно, выйдя из некоторой вершины и войдя в другую, всегда можно выйти из нее по другому ребру , так как степень вершины больше или равна двум. Выйти из вершины по новому ребру невозможно только в том случае, если эта вершина уже встречалась, а это означает, что можно выделить контур из вершин этого графа.
Сетевой моделью называется графическое изображение процессов, выполнение которых приводит к достижению одной или нескольких поставленных целей, с указанием установленных взаимосвязей между этими процессами. Сетевой график представляет собой сетевую модель с расчетными временными параметрами.
Всякий намеченный комплекс работ, необходимых для достижения некоторой цели, называют проектом. Проект (или комплекс работ) подразделяется на отдельные работы. Каждая отдельная работа, входящая в комплекс (проект), требует затрат времени. Некоторые работы могут выполняться только в определенном порядке. При выполнении комплекса работ всегда можно выделить ряд событий, то есть итогов какой-то деятельности, позволяющих приступить к выполнению следующих работ. Если каждому событию поставить в соответствие вершину графа, а каждой работе — ориентированное ребро, то получится некоторый граф. Он будет отражать последовательность выполнения отдельных работ и наступление событий в едином комплексе. Если над ребрами проставить время, необходимое для завершения соответствующей работы, то получится сеть. Изображение такой сети называют сетевым графиком. Сетевой график состоит из двух типов основных элементов: работ и событий. Работа представляет собой выполнение некоторого мероприятия (например, погрузка боезапаса или переход корабля в пункт базирования). Этот элемент сетевого графика связан с затратой времен и расходом ресурсов. Поэтому работа всегда имеет начало и конец.
На сетевом графике работа изображается стрелкой, над которой проставляется ее продолжительность или затрачиваемые ресурсы, или то и другое одновременно. Работа, отражающая только зависимость одного мероприятия от другого, называется фиктивной работой. Такая работа имеет нулевую продолжительность (или нулевой расход ресурсов) и обозначается пунктирной стрелкой.
Начальная и конечная точки работы, то есть начало и окончание некоторого мероприятия, называются событиями. Следовательно, событие, в отличие от работы, не является процессом и не сопровождается никакими затратами времени или ресурсов.
Событие, следующее непосредственно за данной работой, называется последующим событием по отношению к рассматриваемой работе. Событие, непосредственно предшествующее рассматриваемой работе, называется предшествующим.
Наименования "предшествующий" и "последующий" относятся также и к работам. Каждая входящая в данное событие работа считается предшествующей каждой выходящей работе, и наоборот, каждая выходящая работа считается последующей для каждой входящей.
Из определения отношения "предшествующий—последующий" вытекают свойства сетевого графика.
Во-первых, ни одно событие не может произойти до тех пор, пока не будут закончены все входящие в него работы. Во-вторых, ни одна работа, выходящая из данного события, не может начаться до тех пор, пока не произойдет данное событие. И, наконец, ни одна последующая работа не может начаться раньше, чем будут закончены все предшествующие ей.
Событие обозначается кружком с цифрой внутри, определяющей его номер.
Из всех событий, входящих в планируемый процесс, можно выделить два специфических — событие начала процесса, получившее название исходного события, которому присваивается нулевой номер, и событие конца процесса ( завершающее событие), которому присваивается последний номер. Остальные события нумеруются так, чтобы номер предыдущего события был меньше номера последующего.
Для нумерации событий применяется следующий способ. Вычеркиваются все работы, выходящие из события с номером "0", и просматриваются все события, в которых оканчиваются эти вычеркнутые работы. Среди просмотренных находятся события, которые не имеют входящих в них работ (за исключением уже вычеркнутых). Они называются событиями первого ранга и обозначаются (вообще, в произвольном порядке) числами натурального ряда, начиная с единицы (на рисунке 2 это событие 1). Затем вычеркиваются все работы, выходящие из событий первого ранга, и среди них находятся события, не имеющие входящих работ (кроме вычеркнутых). Это — события второго ранга, которые нумеруются следующими числами натурального ряда (например, 2 и 3 на рисунке 2). Проделав таким способом 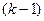 шаг, определяют события шаг, определяют события 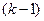 -го ранга , и просматривая события, в которых эти работы заканчиваются, выбирают события, не имеющие ни одной входящей в них работы (кроме вычеркнутых). Это события k-го ранга, и нумеруются они последовательными числами натурального ряда, начиная с наименьшего, еще не использованного числа при предыдущей нумерации на -го ранга , и просматривая события, в которых эти работы заканчиваются, выбирают события, не имеющие ни одной входящей в них работы (кроме вычеркнутых). Это события k-го ранга, и нумеруются они последовательными числами натурального ряда, начиная с наименьшего, еще не использованного числа при предыдущей нумерации на 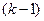 -м шаге. -м шаге.
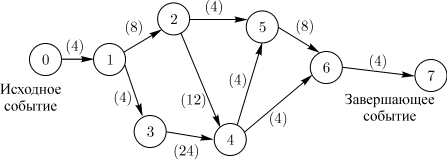
Рисунок 2 – Пример сетевого графика
Сетевой график содержит конечное число событий. Поскольку в процессе вычеркивания движение осуществляется в направлении стрелок (работ), никакое предшествующее событие не может получить номер, больший, чем любое последующее. Всегда найдется хотя бы одно событие соответствующего ранга, и все события получат номера за конечное число шагов.
Работа обычно кодируется номерами событий, между которыми они заключены, то есть парой 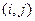 , где i— номер предшествующего события, j— номер последующего события. , где i— номер предшествующего события, j— номер последующего события.
В одно и то же событие могут входить (выходить) одна или несколько работ. Поэтому свершение события зависит от завершения самой длительной из всех входящих в него работ.
Взаимосвязь между работами определяется тем, что начало последующей работы обусловлено окончанием предыдущей. Отсюда следует, что нет работ, не связанных началом и окончанием с другими работами через события.
Последовательные работы и события формируют цепочки (пути), которые ведут от исходного события сетевого графика к завершающему. Например, путь 0®1®2®3®4®5®6®7 сетевого графика, показанного на рисунке 2, включает в себя события 0,1,2,3,4,5,6,7 и работы (0-1), (1-2), (2-5), (5-6), (6-7).
На основании изложенного можно сказать, что ранг события — это максимальное число отдельных работ, входящих в какой-либо из путей, ведущих из нулевого (исходного) события в данное. Так, события первого ранга не имеют путей, состоящих более чем из одной работы, ведущих в них из 0 (например, событие 1 на рисунке 2). События второго ранга связаны с 0 путями, которые состоят не более чем из двух работ, причем для каждого события второго ранга хоть один такой путь обязательно существует. Например, на рисунке 2 событие 4 — событие третьего ранга, так как пути, ведущие в это событие из 0, включают только три работы — (0-1) (1-3)и (3-4) или (0-1),(1-2)и (2-4).
Построенный таким образом сетевой график в терминах теории графов представляет собой направленный граф.
На рисунке изображен сетевой график. Граф, не содержащий циклов и имеющий только один исток и только один сток, называется направленным графом. Сетевой график есть ориентированный связный асимметрический граф с одним истоком, одним стоком и без циклов, то есть это направленный граф. При этом вершинами графа служат события сетевого графика, а дугами (ребрами) — работы сетевого графика.
Продолжительность работы представляет собой, в терминах теории графов, длину дуги. Следовательно, длина пути T— это сумма длин всех дуг, образующих данный путь, то есть 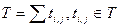 , где символом , где символом 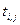 обозначается дуга, которая соединяет вершины i и j и направлена от вершины i к вершине j. обозначается дуга, которая соединяет вершины i и j и направлена от вершины i к вершине j.
Обычно сетевой график строится от исходного события к завершающему, слева направо, то есть каждое последующее событие изображается несколько правее предыдущего.
В планируемых процессах часто встречаются сложные комплексные связи, когда две или более работ выполняются параллельно, но имеют общее конечное событие, или когда для выполнения одной из работ необходимо предварительно выполнить несколько работ, а для другой, выходящей из общего для них события, предварительным условием является выполнение только одной из предшествующих работ и т.д. Изображение в сетевой модели подобных параллельных или дифференцированно зависимых работ выполняется следующим образом.
В случае, когда наступление события (например, 3 на рисунке 3) возможно в результате завершения двух работ (1-3) и (2-4), но в то же время существует событие 4 (рисунок 3), зависящее от завершения только одной из этих работ (например, (2-4)), вводится фиктивная работа (4-3) (см. (рисунок 3).
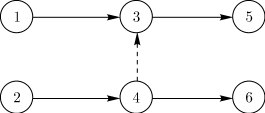
Рисунок 3 – Комплексные связи в сетевом графике
Если одно событие (например, 1 на рисунке 4) служит началом двух (например, (1-2)и (1-3) или нескольких работ, заканчивающихся в другом событии (3 на рисунке 4)), то для их различия также вводится фиктивная работа (2-3). С помощью фиктивной работы в сетевом графике могут быть отражены и двусторонние связи (зависимости).
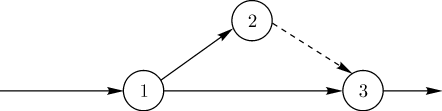
Рисунок 4 – Введение фиктивной работы
Пусть, например, имеются три процесса A, B,C. При этом окончание процесса C зависит от результатов процессов A и B. В этом случае возникают двусторонние зависимости, которые можно изобразить так, как показано на рисунке 5.
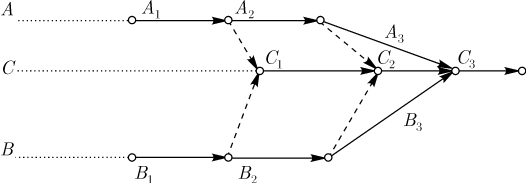
Рисунок 5 – Двусторонние зависимости
Другое правило построения сетевого графика заключается в том, что если несколько работ может начаться не после полного, а после частичного выполнения определенной работы, то последнюю работу целесообразно представить как сумму ее частей, расчлененных событиями ( 1, 2, 3, 4и 5на рисунке 6).
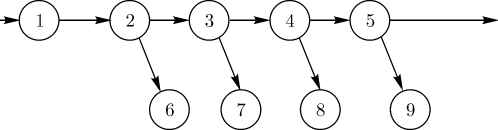
Рисунок 6 – Вариант представления последней работы
Для отображения времени и места поступления дополнительных ресурсов (например, пополнение личного состава, топлива и т.д.) и другой информации на сетевом графике закрашенным кружком изображаются так называемые подставки (рисунок 7). При наличии двух и более работ, выходящих из события, с которым необходимо связать подставку, последняя соединяется с дополнительно введенным событием через фиктивную работу (рисунок 7).
После построения сетевого графика проверяется отсутствие работ, имеющих одинаковые коды. При наличии таких работ вводятся дополнительные события и фиктивные работы. Кроме того, сетевой график должен содержать только одно исходное событие и только одно завершающее событие.
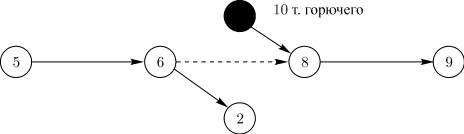
Рисунок 7 – Подставки в сетевом графике
Если эти условия не выполнены, то необходимо добавить еще одно исходное событие и соединить его стрелками с имеющимися несколькими начальными событиями или добавить еще одно конечное событие, к которому ведут стрелки от нескольких имеющихся конечных событий.
Сетевой график не должен иметь циклов, то есть таких путей, в которых конец последней работы совпадает с началом первой работы. Сетевой график, имеющий хотя бы один цикл, не может быть реализован, так как ни одна из работ, входящих в такой цикл, никогда не может начаться.
Анализ сетевой модели
Параметры сетевой модели. Параметрами сетевой модели являются:
1) наиболее ранее возможное время наступления j-го события, обозначаемое символом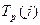 ; ;
2) самое позднее допустимое время наступления i-го события, обозначаемое символом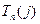 ; ;
3) резерв времени данного события, обозначаемый символом 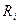 ; ;
4) полный резерв времени работы (i,j), обозначаемый символом 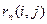 ; ;
5) свободный резерв времени работы (i,j), обозначаемый символом 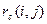 . .
Наиболее раннее возможное время наступления j-го события определяется следующий рекуррентной формулой:
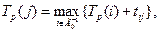
где 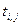 — продолжительность (i,j)-й работы; — продолжительность (i,j)-й работы;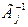 — множество событий, предшествующих j-му событию. — множество событий, предшествующих j-му событию.
Вычисления по формуле выполняются шаг за шагом, двигаясь в порядке нумерации событий.
Резервом времени данного события называется разность между 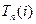 и и 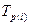 , которая вычисляется по формуле , которая вычисляется по формуле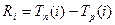 . .
Полный резерв времени работы (i, j) вычисляется по формуле
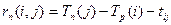
Свободный резерв времени работы (i, j) вычисляется по формуле
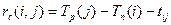
1.3 Нахождение максимального потока в сети
Транспортной сетью называется конечный Связный орграф G(V, E) без петель, каждой дуге которого поставлено в соответствие некоторое неотрицательное число c(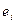 ), называемое пропускной способностью дуги, и существует: ), называемое пропускной способностью дуги, и существует:
1) ровно одна вершина 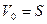 , в которую не заходит ни одна дуга, называемая источником или началом сети; , в которую не заходит ни одна дуга, называемая источником или началом сети;
2) ровно одна вершина  , из которой не выходит ни одной дуги; эта вершина называется стоком или концом сети. , из которой не выходит ни одной дуги; эта вершина называется стоком или концом сети.
Потоком сети называется неотрицательная функция f(1) такая, что f(e) меньше или равно c(e). (Поток не может превышать пропускную способность дуги.)
Дуга 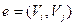 называется насыщенной потоком f, если называется насыщенной потоком f, если 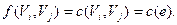 (Поток называется полным, если содержит насыщенную дугу f(e)=c(e).) (Поток называется полным, если содержит насыщенную дугу f(e)=c(e).)
Разрезом L сети G(V,E) называется множество насыщенных дуг, отделяющих источник s от стока t.
Теорема Форда-Фалкерсона.
Пусть D – транспортная сеть, 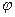 - допустимый поток в этой сети, - допустимый поток в этой сети, 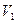 - множество вершин - множество вершин 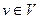 таких, что длина минимального пути из таких, что длина минимального пути из 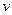 в в 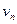 в орграфе приращений в орграфе приращений 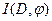 равна нулю. Тогда, если равна нулю. Тогда, если 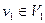 , то , то 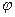 - максимальный поток, величина которого равна - максимальный поток, величина которого равна 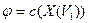 . .
Пусть 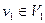 . Тогда выполняется равенство . Тогда выполняется равенство
 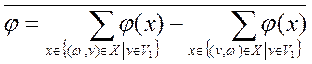 (1) (1)

Если 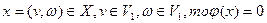 , так как в противном случае, используя , так как в противном случае, используя 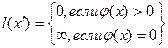 имеем имеем 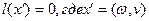 , а следовательно, в силу , а следовательно, в силу 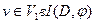 существует путь нулевой длины из существует путь нулевой длины из 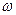 в в 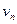 , что противоречит условию , что противоречит условию 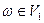 . Но тогда из (1) получаем . Но тогда из (1) получаем
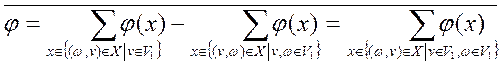
Следствие 1. Используя теорему Форда-Фалкерсона получаем, что величина максимального потока в транспортной сети равна пропускной способности минимального разреза.
Следствие 2. Пусть 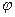 - допустимый поток в транспортной сети D. Тогда, если длина минимального пути из v1 в vn в орграфе приращений - допустимый поток в транспортной сети D. Тогда, если длина минимального пути из v1 в vn в орграфе приращений 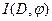 равна бесконечности, то равна бесконечности, то 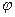 - максимальный поток. - максимальный поток.
Алгоритм решения можно представить следующим образом.Сначала будем строить полный поток, затем проверим, можно ли его увеличить. Если нет, то этот поток является максимальным. Если же его можно увеличить, то будем строить другой полный поток и т.д. Решать задачу будем с помощью метода расстановки пометок.
Две основные процедуры (операции алгоритма):
· операция расстановки пометок;
· операция изменения потока.
Рассмотрим первую процедуру. Для каждой вершины данной сети нужно приписать пометку, которая имеет следующий вид: 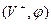 или или 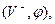 где где 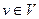 , а , а 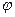 – натуральное число или бесконечность. Вообще возможны три состояния вершины: – натуральное число или бесконечность. Вообще возможны три состояния вершины:
1) не помечена;
2) помечена, но не просмотрена;
3) помечена и просмотрена.
Расставлять пометки начнем с источника S. Он получит пометку 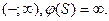 Источник помечен, но не просмотрен. Остальные вершины не помечены. Чтобы источник S был помечен и просмотрен, надо поместить все вершины, смежные с S. Источник помечен, но не просмотрен. Остальные вершины не помечены. Чтобы источник S был помечен и просмотрен, надо поместить все вершины, смежные с S.
Вершина 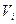 получит пометку получит пометку 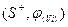 , где , где 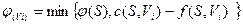 . .
Теперь все вершины 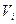 смежные с S, помечены, но не просмотрены. А вершина S помечена и просмотрена. Начнём просматривать ту из вершин смежные с S, помечены, но не просмотрены. А вершина S помечена и просмотрена. Начнём просматривать ту из вершин 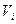 , которая имеет наименьший индекс. Для этого нужно расставить пометки вершинам, смежным с , которая имеет наименьший индекс. Для этого нужно расставить пометки вершинам, смежным с 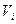 . Если для вершины . Если для вершины 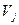 выполняется следующее условие выполняется следующее условие 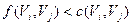 , то она получит метку , то она получит метку 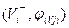 , где , где 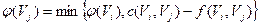 . Если же для вершины . Если же для вершины 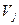 выполняется условие выполняется условие 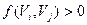 , то , то 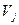 получает метку получает метку 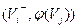 , где , где 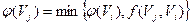 . Далее просматриваем следующую вершину, и так до тех пор, пока не пометим сток t или же пока нельзя будет больше пометить ни одной вершины, сток при этом останется не помеченным. Если сток окажется не помеченным, то процесс нахождения максимального потока в сети можно считать законченным, а если сток помечен, то нужно переходить к процедуре 2. . Далее просматриваем следующую вершину, и так до тех пор, пока не пометим сток t или же пока нельзя будет больше пометить ни одной вершины, сток при этом останется не помеченным. Если сток окажется не помеченным, то процесс нахождения максимального потока в сети можно считать законченным, а если сток помечен, то нужно переходить к процедуре 2.
Рассмотрим процедуру изменения потока. Если вершина 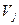 имеет пометку имеет пометку 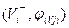 , то , то 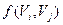 заменяем на заменяем на 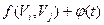 , если же вершина , если же вершина 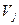 имеет пометку имеет пометку 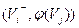 , то , то 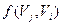 заменяем на заменяем на 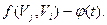
Переходим к следующей вершине и так до тех пор, пока не достигнем источника S. Здесь изменение потока прекращается. Далее переходим к процедуре 1 и так до тех пор, пока величину потока уже нельзя изменить.
Дана сеть G(V,E) с источником S и стоком t. Пропускные способности дуг указаны. Найти максимальный поток из S в t.
Функция 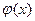 , определенная на множестве X дуг транспортной сети D и принимающая целочисленные значения, называется допустимым потоком (или просто потоком) в транспортной сети D, если: , определенная на множестве X дуг транспортной сети D и принимающая целочисленные значения, называется допустимым потоком (или просто потоком) в транспортной сети D, если:
•для любой дуги 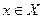 величина величина 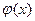 , называемая потоком по дуге , называемая потоком по дуге 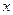 , удовлетворяет условию , удовлетворяет условию 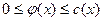 ; ;
•для любой промежуточной вершины v выполняется равенство
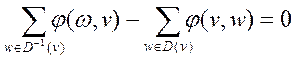
т.е. сумма потоков по дугам, заходящим в v, равна сумме потоков по дугам, исходящим из v.
Для любого допустимого потока 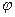 в транспортной сети D выполняется равенство: в транспортной сети D выполняется равенство:
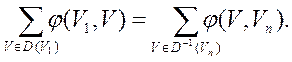
По определению допустимого потока 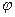 имеем: имеем:
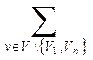 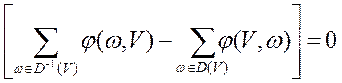
Заметим, что для каждой дуги 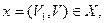 где где 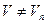 , величина , величина 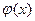 входит в левую часть равенства лишь один раз и при этом со знаком плюс. Аналогично для каждой дуги входит в левую часть равенства лишь один раз и при этом со знаком плюс. Аналогично для каждой дуги  , величина , величина 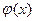 входит в левую часть равенства лишь один раз и при этом со знаком минус. С другой стороны, для каждой дуги входит в левую часть равенства лишь один раз и при этом со знаком минус. С другой стороны, для каждой дуги 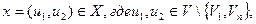 величина величина 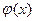 входит в левую часть равенства один раз со знаком плюс (при входит в левую часть равенства один раз со знаком плюс (при 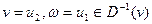 ) и один раз со знаком минус (при ) и один раз со знаком минус (при 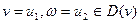 ), что в сумме даёт нулевой вклад в левую часть равенства. ), что в сумме даёт нулевой вклад в левую часть равенства.
Величиной потока 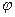 в транспортной сети D называется величина в транспортной сети D называется величина 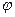 , равная сумме потоков по всем дугам, заходящим в , равная сумме потоков по всем дугам, заходящим в 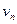 , или, что то же самое – величина, равная сумме потоков по всем дугам, исходящим из , или, что то же самое – величина, равная сумме потоков по всем дугам, исходящим из
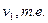
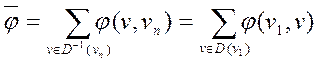
Пусть 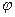 - допустимый поток в транспортной сети D. Дуга - допустимый поток в транспортной сети D. Дуга 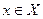 называется насыщенной, если поток по ней равен её пропускной способности, т.е. если называется насыщенной, если поток по ней равен её пропускной способности, т.е. если  . Поток . Поток 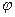 называется полным, если любой путь в D из называется полным, если любой путь в D из 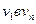 содержит, по крайней мере, одну насыщенную дугу. содержит, по крайней мере, одну насыщенную дугу.
Поток 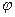 называется максимальным, если его величина называется максимальным, если его величина 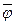 принимает максимальное значение по сравнению с другими допустимыми потоками в транспортной сети D. принимает максимальное значение по сравнению с другими допустимыми потоками в транспортной сети D.
Очевидно, что максимальный поток 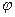 обязательно является полным (т.к. в противном случае в D существует некоторая простая цепь обязательно является полным (т.к. в противном случае в D существует некоторая простая цепь 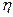 из V1 в Vn, не содержащая насыщенных дуг, а следовательно, можно увеличить на единицу потоки по всем дугам из из V1 в Vn, не содержащая насыщенных дуг, а следовательно, можно увеличить на единицу потоки по всем дугам из 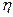 и тем самым увеличить на единицу и тем самым увеличить на единицу 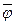 , что противоречит условию максимальности потока). Обратная же, вообще говоря, неверно. Существуют полные потоки, не являющиеся максимальными. Тем на менее полный поток можно рассматривать как некоторое приближение к максимальному потоку. , что противоречит условию максимальности потока). Обратная же, вообще говоря, неверно. Существуют полные потоки, не являющиеся максимальными. Тем на менее полный поток можно рассматривать как некоторое приближение к максимальному потоку.
Введем для заданной транспортной сети D и допустимого потока 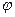 в этой сети орграф приращений в этой сети орграф приращений 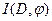 , имеющий те же вершины, что и сеть D. Каждой дуге , имеющий те же вершины, что и сеть D. Каждой дуге 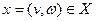 транспортной сети D в орграфе приращений транспортной сети D в орграфе приращений 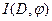 соответствует две дуги: соответствует две дуги: 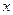 и и 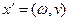 - дуга, противоположная по направлению дуге - дуга, противоположная по направлению дуге 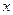 . Припишем дугам . Припишем дугам 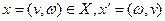 орграфа приращений орграфа приращений 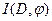 длину длину 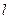 : :
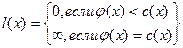
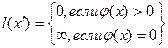
т.е. орграф 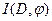 является нагруженным. При этом очевидно, что длина любого пути из является нагруженным. При этом очевидно, что длина любого пути из 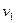 в в 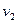 в орграфе в орграфе 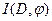 равна либо 0, либо бесконечности. равна либо 0, либо бесконечности.
Важным следствием теоремы Форда-Фалкерсона является Алгоритм построения максимального потока в транспортной сети.
Алгоритм:
Шаг 1. Полагаем i=0. Пусть 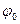 - любой допустимый поток в транспортной сети D (например, полный, можно начинать с нулевого потока: - любой допустимый поток в транспортной сети D (например, полный, можно начинать с нулевого потока: 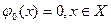 ). ).
Шаг 2. По сети D и потоку 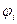 строим орграф приращений строим орграф приращений 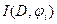 . .
Шаг 3. Находим простую цепь 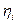 , являющуюся минимальным путем из , являющуюся минимальным путем из 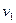 в в 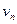 в нагруженном орграфе в нагруженном орграфе 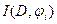 . Если длина этой цепи равна бесконечности, то поток . Если длина этой цепи равна бесконечности, то поток 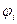 максимален, и работа алгоритма закончена. В противном случае увеличиваем поток ввдоль цепи максимален, и работа алгоритма закончена. В противном случае увеличиваем поток ввдоль цепи 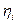 на максимально допустимую величину на максимально допустимую величину 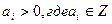 , такую, что при этом сохраняется условие 1 допустимого потока (для любой дуги , такую, что при этом сохраняется условие 1 допустимого потока (для любой дуги 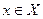 величина величина 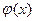 , называемая потоком по дуге х, удовлетворяет условию , называемая потоком по дуге х, удовлетворяет условию 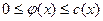 ). В силу ). В силу 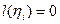 , используя , используя 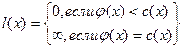 и и 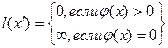 , получаем, что указанная величина , получаем, что указанная величина 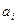 существует. В результате меняется поток в транспортной сети D, т.е. от потока существует. В результате меняется поток в транспортной сети D, т.е. от потока 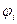 мы перешли к потоку мы перешли к потоку 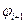 , и при этом , и при этом 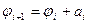 . Присваеваем . Присваеваем 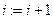  и переходим к шагу 2. и переходим к шагу 2.
На практике часто возникают задачи определения максимального количества нефти, которое может быть доставлено по трубопроводу за какое-то время. Аналогичными являются задачи определения максимальной пропускной способности системы автомагистралей или энергосети. Формально эти проблемы сводятся к задачи построения максимального потока в сети. Мы же конкретней остановимся на задачи определения максимальной пропускной способности нефтепровода.
Пусть требуется построить увеличивающую цепь для сети S= (N,U), представленной на рисунке 8.
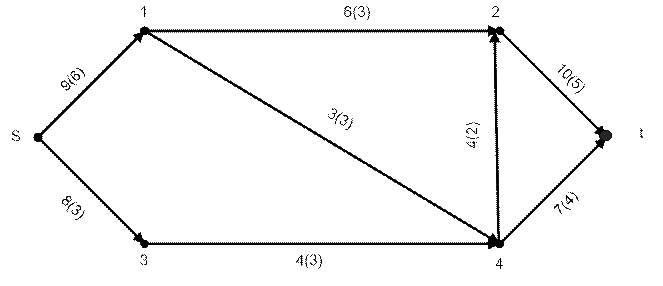
Рисунок 8 – Построение увеличивающей сети
Над каждой дугой указана ее пропускная способность и в скобках - величина потока по этой дуге.
Цепь (s,1,2,3,4,t) является увеличивающей, так как все ее дуги – допустимые:
1) дуга (s,1) – увеличивающая, так как она проходит по направлению потока и поток по ней меньше ее пропускной способности: 6<9;
2) дуга (1,2) – также увеличивающая дуга: 3<6;
3) дуга (2,4) – уменьшающая, так как она проходит против движения потока и поток по ней 2>0;
4) дуга (4,t) – увеличивающая: 4<7;
Построим увеличивающую цепь для сети, представленной на рисунке 9.

Рисунок 9 – Построение увеличивающей сети
Цепь (s,3,2,t) – увеличивающая, так как все ее дуги являются допустимыми увеличивающими дугами.
Определение максимального потока основано на увеличении вдоль увеличивающей цепи на величину 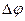 . .
Алгоритм построения максимального потока включает в себя следующую последовательность:
1) задание начального значения потока. Удобно задавать нулевое начальное значение (V0
=0);
2) построение увеличивающей цепи от входа к выходу сети. Если такой цепи нет, то максимальный поток построен, и его величина Vmax
=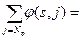 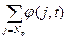 ,в противном случае переходят к пункту 3 ,в противном случае переходят к пункту 3
3) увеличение вдоль построенной цепи значения потока на максимально возможную величину 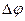 , при этом по каждой увеличивающей дуге поток увеличится на , при этом по каждой увеличивающей дуге поток увеличится на 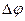 , а по каждой уменьшающей дуге уменьшается на , а по каждой уменьшающей дуге уменьшается на 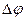 . .
Определим максимальный поток для сети, показанной на рисунке 8. Начальный поток в сети задан, следовательно пункт 1 алгоритма выполнен.
Увеличим поток вдоль цепи (s,1,2,4,t). Вдоль дуги (s,1) поток можно увеличить на разницу между пропускной способностью этой дуги 9 и уже проходящим по ней потоком 6 (9 – 6 = 3).
Вдоль дуги (1,2) аналогичным образом поток можно увеличить на 3.
Дуга (2,4) является уменьшающей. Максимальная величина, на которую можно увеличить поток по ней равна 2, т.е. значению уже проходящего по ней потока. По дуге (4,t) поток можно увеличить на 3.
Таким образом, максимальная величина 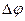 , на которую можно увеличить поток, составляет наименьшую из величин , на которую можно увеличить поток, составляет наименьшую из величин 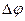 = min(3,3,2,3) = 2, при этом на каждой увеличивающей дуге поток увеличивается на эту величину, а по каждой уменьшающей – уменьшается. = min(3,3,2,3) = 2, при этом на каждой увеличивающей дуге поток увеличивается на эту величину, а по каждой уменьшающей – уменьшается.
Новое значение потока записано в скобках над дугой ( рисунок 10).
После такого перераспределения значение потока увеличилось на 2 и стало равным V = 11(8+3=6+5), а условие сохранения потока в вершинах сети по-прежнему выполняется. Заметим, что если увеличить поток не на 2, а на 3, то на дуге (4,2) получим отрицательное значение -1, что противоречит свойству неотрицательности потока. Рассмотрим теперь цепь (s,1,2,t). Эта цепь увеличивающая, т. к. все дуги – допустимые. Поток вдоль этой цепи можно увеличить на 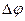 = min (9 – 8;6 – 5; 10 – 5) = 1. = min (9 – 8;6 – 5; 10 – 5) = 1.
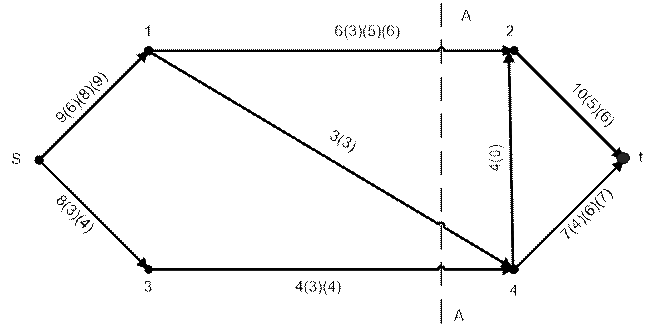
Рисунок 10 – Построение максимального потока
Новое значение потока указано во вторых скобках на рисунке 10.
Заметим, что если допустить увеличение потока на 5, то поток по дугам (s,1) и (1,2) превзойдет пропускную способность этих дуг.
Затем рассмотрим цепь (s,3,4,t): 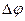 =min (8 – 3; 4 – 3; 7 – 6) = 1. =min (8 – 3; 4 – 3; 7 – 6) = 1.
Больше увеличивающих цепей нет, следовательно максимальный поток построен. Его величина Vmax = 11 + 1 + 1 = 9 + 4 = 6 + 7 = 13.
Минимальный разрез АА, соответствующий этому потоку, содержит дуги: {(1,2);(1,4);(3,4)}, а его пропускная способность 6 + 3 + 4 = 13 соответствует величине максимального потока.
Следовательно, что значение 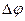 , на которое увеличивается поток вдоль увеличивающей цепи, определяется следующим образом: , на которое увеличивается поток вдоль увеличивающей цепи, определяется следующим образом:
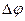 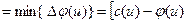 или или 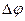 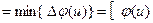 , в зависимости от типа дуги. , в зависимости от типа дуги.
Таким образом, мы получаем сетевую модель нефтепровода максимальной пропускной способности.
Выводы и рекомендации
Использование сетевых методов дает возможность увязать во времени программу производства работ, планировать последовательность их выполнения, выявлять и устранять возникающие в процессе реализации нарушения. Анализ сетевых моделей позволяет: определить, от каких операций и в какой степени зависит срок выполнения всей программы; предвидеть появление "узких мест"; выделить второстепенные, с точки зрения времени реализации программы, работы, сокращение продолжительности которых не только не приведет к уменьшению времени выполнения всей совокупности операций, но и может привести к увеличению стоимости работ и простоев рабочих и оборудования. Кроме того, сетевые методы позволяют дать обоснованные, в том числе и с экономической точки зрения, ответы на вопросы организации выполнения работ программы.
Библиографический список.
1. Беллман Р. Динамическое программирование. – М., 2008.
2. Ромакин М.И. Оптимизация планирования производства: экономико-математические модели и методы. М., Финансы и статистика, 2007.
3. Майника Э. Алгоритмы оптимизации на сетях и графах. – М., Мир, 2009.
4. Лотов А.В. Введение в экономико-математическое моделирование. – М., Наука, 2006.
5. Справочник по математике для экономистов. Под ред. В.И. Ермакова. М., – Высшая школа, 2008.
|