ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
КАФЕДРА ЭММ
Контрольная работа
по дисциплине «Экономико-математическим моделям»
Вариант № 1
Исполнитель:
Специальность: Бухгалтерский учет, анализ и аудит
Группа:
№ зачетной книжки:
Руководитель:
Задача 1
1.1.
Инвестор, располагающий суммой в 300 тыс. ден. ед., может вложить свой капитал в акции автомобильного концерна А и строительного предприятия В. Чтобы уменьшить риск, акций А должно быть приобретено по крайней мере в два раза больше, чем акций В, причем последних можно купить не более чем на 100 тыс. ден. ед.
Дивиденды по акциям А составляют 8% в год, по акциям В – 10%. Какую максимальную прибыль можно получить в первый год?
Решение:
1) Введем необходимые обозначения:
Пусть Xi
– вложения (количество денежных у. е.) в ценную бумагу вида i.
i – вид ценной бумаги ( i = 1, 2, 3, 4, 5, 6)
Х1
– вложения в акции А,
Х5
– вложения в краткосрочные облигации и т. д.
Ci
– доход, приносимый ценной бумагой вида i, в коэффициентах:
Например, С2
= 0,12 – доход от акции В, и т. п.
| Вложение |
№ бумаги ( i ) |
Доход, коэффициент |
| Акции А |
1 |
0,15 |
| Акции В |
2 |
0,12 |
| Акции С |
3 |
0,09 |
| Долгосрочные облигации |
4 |
0,11 |
| Краткосрочные облигации |
5 |
0,08 |
| Срочный вклад |
6 |
0,06 |
Требуется найти вектор Х с координатами:
X ( X1
; X2
; X3
; X4
; X5
; X6
),
2) Цель задачи: максимизировать годовой доход от портфеля выбранных бумаг.
F (X) = ∑ Xi
* Сi
(mах)
F (X) = 0,15 X1
+ 0,12 X2
+ 0,09 X3
+ 0,11 X4
+ 0,08 X5
+ 0,06 X6
3) Ограничения:
- Все 300 тыс. руб. должны быть инвестированы:
- ∑ Xi
= 500;
- По крайней мере 100 тыс. руб. должны быть на срочном вкладе:
o Х6
> = 100;
- По крайней мере, 25 % средств, инвестированных в акции, должны быть инвестированы в акции с низким риском: т. е. X3
должны составлять по крайней мере четверть от общей суммы вклада в акции:
- X3
> = 0,25 ∑ (X1
; X2
; X3
);
- В облигации нужно инвестировать по крайней мере столько же, сколько в акции:
- ∑ (X4
; X5
) > = 0,25 ∑ (X1
; X2
; X3
);
- Не более чем 125 тыс. руб. должно быть вложено в бумаги с доходом менее 10 % - это акции С, краткосрочные облигации и срочный вклад:
X3
+ X5
+ X6
< = 125.
Значит, ограничения выглядят так:
X1
+ X2
+ X3
+ X4
+ X5
+ X6
= 500;
Х6
> = 100;
X3
> = 0,25 ∑ (X1
; X2
; X3
);
∑ (X4
; X5
) > = 0,25 ∑ (X1
; X2
; X3
);
Реклама

X3
+ X5
+ X6
< = 125;
Xi
> = 0 ( i = 1, 2, 3, 4, 5, 6).
Ожидаемый годовой доход по той или иной бумаге (особенно по акциям) – это не более чем оценка. Оптимальный портфель и ожидаемая величина дохода от портфеля выбранных бумаг чувствительны к этим оценкам. Наиболее сильно влияет на оценку суммарного ожидаемого дохода ценная бумага
Задача 2
2.1.
Для изготовления четырех видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и цены реализации единицы каждого вида продукции приведены в таблице.
Тип сырья
|
Нормы расхода сырья на ед. продукции
|
Запасы
сырья
|
| А |
Б |
В |
Г |
I
II
III
|
1
1
1
|
2
1
3
|
1
2
3
|
0
1
2
|
18
30
40
|
| Цена изделия |
12 |
7 |
18 |
10 |
Требуется:
1) Сформулировать прямую оптимизационную задачу на максимум выручки от реализации готовой продукции, получить оптимальный план выпуска продукции.
2) Сформулировать двойственную задачу и найти ее оптимальный план с помощью теорем двойственности.
3) Пояснить нулевые значения переменных в оптимальном плане.
4) На основе свойств двойственных оценок и теорем двойственности:
- проанализировать использование ресурсов в оптимальном плане исходной задачи;
- определить, как изменятся выручка и план выпуска продукции при увеличении запасов сырья I и II вида на 4 и 3 единицы соответственно и уменьшении на 3 единицы сырья III вида;
- оценить целесообразность включения в план изделий "Д" ценой 10 ед., на изготовление которого расходуется по две единицы каждого вида сырья.
Решение:
1. Построим ЭММ задачи. Обозначим через хi
- объем выпуска готовой продукции j-го вида. С учетом критерия оптимальности «max выручки», будем иметь ЭММ задачи:
maxf (х) = 12х1
+ 7х2
+ 18 х3
+ 10 х4
Ограничения отражают условия ограниченности запасов сырья.
1х1
+ 2х2
+ 1х3
≤ 18 - затраты 1-го вида ресурсов на выпуск всей продукции
1х1
+ 2х3
+ 1х2
+ 1х4
≤ 30 - затраты 2-го вида ресурсов на выпуск всей продукции
1х1
+ 3х2
+ 3х3
+ 2х4
≤ 40 - затраты 3-го вида ресурсов на выпуск всей продукции
хj
≥ 0, 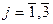
Реализуя эту ЭММ задачу средствами Excel получим решение:
| Переменные |
| X1 |
X2 |
X3 |
X4 |
| значение |
18 |
0 |
0 |
1 |
ЦФ |
| коэф. В ЦФ |
12 |
7 |
18 |
10 |
226 |
| Ограничения |
| Вид ресурса |
левая часть |
знак |
правая часть |
| 1 |
1 |
2 |
1 |
0 |
18 |
<= |
18 |
| 2 |
1 |
1 |
2 |
1 |
19 |
<= |
30 |
| 3 |
1 |
3 |
3 |
2 |
20 |
<= |
40 |
Оптимальный план выпуска продукции: Х*
= (18, 0, 0,11),
f (Х*
) = 226
2. Для определения двойственных оценок построим двойственную задачу:
min φ (y) = 18y1
+ 30y2
+ 40y3
1y1
+ 1y2
+ 1y3
≥ 12
2y1
+ 1y2
+ 3y3
≥ 7
1y1
+ 2y2
+ 3y3
≥ 18
0y1
+ 1y2
+ 1y3
≥ 10
y1
≥ 0, y2
≥ 0, y3
≥ 0
Реклама

Реализуя эту ЭММ задачу средствами Excel получим решение:
| Переменная |
у1 |
у2 |
у3 |
| 2 |
10 |
0 |
| Коэффициент |
18 |
30 |
40 |
336 |
| 1 |
1 |
1 |
12 |
12 |
| 2 |
1 |
3 |
17 |
17 |
| 1 |
2 |
3 |
18 |
18 |
| 0 |
1 |
1 |
10 |
10 |
Чтобы оценить целесообразность включения в план изделия четвертого вида необходимо произвести оценку затрат на единицу продукции:
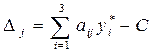
2*1 + 10*1 + 1*0 + 2= 14 > 12
Изделие не выгодно включать в план, т.к. затраты на его изготовление не покрываются ценой продажи.
Задача 3
3.1.
Промышленная группа предприятий (холдинг) выпускает продукцию трех видов, при этом каждое из трех предприятий группы специализируется на выпуске продукции одного вида: первое предприятие специализируется на выпуске продукции первого вида, второе предприятие - продукции второго вида; третье предприятие - продукции третьего вида. Часть выпускаемой продукции потребляется предприятиями холдинга (идет на внутреннее потребление), остальная часть поставляется за его пределы (внешним потребителям, является конечным продуктом). Специалистами управляющей компании получены экономические оценки аij
(i=1,2,3; j=1,2,3) элементов технологической матрицы А (норм расхода, коэффициентов прямых материальных затрат) и элементов yi
вектора конечной продукции Y.
Требуется:
1) Проверить продуктивность технологической матрицы A=(аij
) (матрицы коэффициентов прямых материальных затрат).
2) Построить баланс (заполнить таблицу) производства и распределения продукции предприятий холдинга.
Исходные данные приведены в таблице
| Предприятия (виды продукции) |
Коэффициенты прямых затрат аij
|
Конечный продукт |
| 1 |
2 |
3 |
| 1 |
0,1 |
0,2 |
0,1 |
200 |
| 2 |
0,2 |
0,1 |
0,0 |
150 |
| 3 |
0,0 |
0,2 |
0,1 |
250 |
Решение:
| 0,1 |
0,2 |
0,1 |
200 |
| А = |
0,2 |
0,1 |
0,0 |
Y = |
150 |
| 0,0 |
0,2 |
0,1 |
250 |
1. Проведем оценку по первому признаку продуктивности: матрица (Е-А) неотрицательно обратима, т.е. существует обратная матрица и все ее элементы неотрицательны. Определим матрицу (Е-А). С помощью функции МОБР Мастера функций Exсel найдем обратную матрицу. Поскольку все элементы матрицы В неотрицательны, то матрица А продуктивна.
| 1. Межотраслевые поставки продукции |
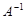
|
-5 |
0 |
5 |
| 10 |
10 |
-10 |
| -5 |
-20 |
15 |

|
1 |
2,22E-16 |
1,11022E-16 |
| -4,44089E-16 |
1 |
0 |
| 0 |
-4,4E-16 |
1 |
| E-A |
0,9 |
-0,2 |
-0,1 |
| -0,2 |
0,9 |
0 |
| -0,3 |
-0,2 |
0,9 |
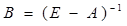
|
1,223564955 |
0,302115 |
0,135951662 |
| 0,271903323 |
1,178248 |
0,03021148 |
| 0,468277946 |
0,362538 |
1,163141994 |
| X |
324,0181269 |
| 238,6706949 |
| 438,8217523 |
| Xij |
32,40181269 |
64,80363 |
32,40181269 |
| 47,73413897 |
23,86707 |
0 |
| 131,6465257 |
87,76435 |
43,88217523 |
2. Руководствуясь балансовым методом планирования и экономическим смыслом прямых материальных затрат будем иметь следующую модель межотраслевого баланса. Для решения воспользуемся пакетом Exсel. В результате решения будем иметь следующие объемы валового продукта по предприятиям.
Схема межотраслевого баланса будет выглядеть следующим образом:
| Производящие отрасли |
Потребляющие отрасли |
Конечный продукт |
Валовый продукт |
| 1 |
2 |
3 |
| 1 |
63,86 |
95,79 |
0 |
120 |
319,31 |
| 2 |
135,48 |
45,14 |
90,29 |
250 |
451,49 |
| 3 |
30,27 |
0 |
90,82 |
180 |
302,75 |
| Условно чистая продукция |
421,2 |
400,84 |
483,86 |
550 |
| Валовой продукт |
319,31 |
451,49 |
302,75 |
1073,55 |
Изобразим это на графике: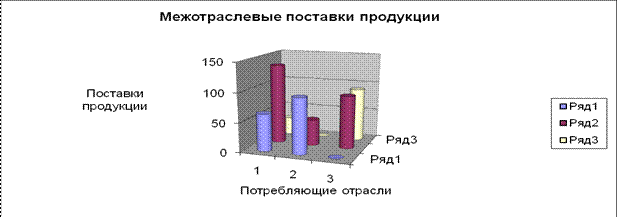
Задача 4.1
4.1.
В течение девяти последовательных недель фиксировался спрос Y(t) (млн. р.) на кредитные ресурсы финансовой компании. Временной ряд Y(t) этого показателя (повариантно) приведен ниже в таблице
Номер варианта
|
Номер наблюдения ( t = 1,2,…,9)
|
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 1 |
10 |
14 |
21 |
24 |
33 |
41 |
44 |
47 |
49 |
Требуется:
1) Проверить наличие аномальных наблюдений.
2) Построить линейную модель 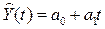 , параметры которой оценить МНК ( , параметры которой оценить МНК (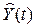 - расчетные, смоделированные значения временного ряда). - расчетные, смоделированные значения временного ряда).
3) Оценить адекватность построенных моделей, используя свойства независимости остаточной компоненты, случайности и соответствия нормальному закону распределения (при использовании R/S-критерия взять табулированные границы 2,7—3,7).
4) Оценить точность моделей на основе использования средней относительной ошибки аппроксимации.
5) По двум построенным моделям осуществить прогноз спроса на следующие две недели (доверительный интервал прогноза рассчитать при доверительной вероятности р = 70%).
6) Фактические значения показателя, результаты моделирования и прогнозирования представить графически.
Вычисления провести с одним знаком в дробной части. Основные промежуточные результаты вычислений представить в таблицах (при использовании компьютера представить соответствующие листинги с комментариями).
Решение:
1. Введем исходные данные.
Таблица 3.1
| t |
yt,
факт. |
| 1 |
10 |
| 2 |
14 |
| 3 |
21 |
| 4 |
24 |
| 5 |
33 |
| 6 |
41 |
| 7 |
44 |
| 8 |
47 |
| 9 |
49 |
Для проверки наличия аномальных наблюдений воспользуемся пакетом Excel. В результате решения будем иметь следующие данные:
Таблица 3.2
| /yt
.-yt-1/
|
с.к.о. |
Характеристика Ирвина |
| 5 |
10,9023 |
0,45861696 |
| 2 |
0,183446784 |
| 4 |
0,366893568 |
| 6 |
0,550340352 |
| 2 |
0,183446784 |
| 6 |
0,550340352 |
| 2 |
0,183446784 |
| 5 |
0,45861696 |
Чтобы найти среднее квадратическое отклонение воспользуемся функцией СТАНДОТКЛОН Мастера функций Excel.
Табличное значение Величины Ирвина равно 1,5 , следовательно, в соответствии с методом Ирвина аномальные наблюдения не выявлены.
2. Построим линейную однопараметрическую модель регрессии Y от t. Для проведения регрессионного анализа воспользуемся надстройкой Excel Анализ данных. В результате получим следующее:
Таблица 3.3
| Регрессионная статистика |
| Множественный R |
0,996406256 |
| R-квадрат |
0,992825427 |
| Нормированный R-квадрат |
0,991800487 |
| Стандартная ошибка |
0,987219922 |
| Наблюдения |
9 |
Таблица 3.4
| Дисперсионный анализ |
| df |
SS |
MS |
F |
Значимость F |
| Регрессия |
1 |
944,0666667 |
944,0666667 |
968,6677524 |
9,12922E-09 |
| Остаток |
7 |
6,822222222 |
0,974603175 |
| Итого |
8 |
950,8888889 |
Таблица 3.5
| Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
Нижние 95% |
Верхние 95% |
Нижние 95,0% |
Верхние 95,0% |
| Y-пересечение |
4,06 |
0,717198646 |
5,654717251 |
0,000770691 |
2,359650245 |
5,751460866 |
2,359650245 |
5,751460866 |
| t |
3,97 |
0,127449544 |
31,12342771 |
9,12922E-09 |
3,665296384 |
4,268036949 |
3,665296384 |
4,268036949 |
Вывод остатка
Таблица 3.6
| Наблюдение |
Предсказанное yt, факт. |
Остатки |
| 1 |
8,02 |
-0,02 |
| 2 |
11,99 |
1,01 |
| 3 |
15,96 |
-0,96 |
| 4 |
19,92 |
-0,92 |
| 5 |
23,89 |
1,11 |
| 6 |
27,86 |
-0,86 |
| 7 |
31,82 |
1,18 |
| 8 |
35,79 |
-0,79 |
| 9 |
39,76 |
0,24 |
| Ср. знач. |
0,00 |
Во втором столбце таблицы 3.5 содержатся коэффициенты уравнения регрессии а0
, а1
,. Уравнение регрессии зависимости Yt
(спрос на кредитные ресурсы) от t1
(время) имеет вид:
Y(t) = 4,06 + 3,97t
3. Оценка адекватности модели.
1) С помощью функции СРЗНАЧ Мастера функций Excel по таблице 3.6 найдем среднее значение остатков.
2) Построим график остатков. По графику видно, что P=7 больше 2, следовательно свойство случайности остатков выполняется.
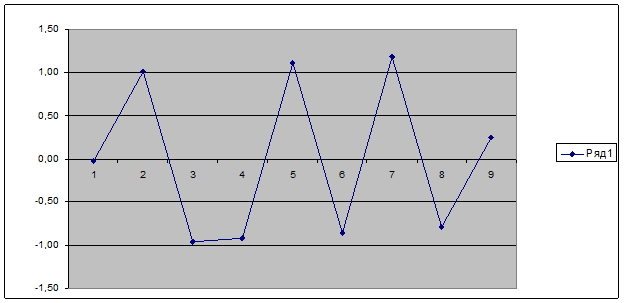
Рис. 3.1 График остатков
3) С помощью функции КОРРЕЛ Мастера функций Excel по таблице 3.6 найдем коэффициент корреляции.
По след. формуле найдем tрасч.
:
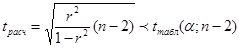
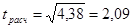
Коэффициент корреляции r = -0,62 незначим, поскольку
tрасч.
=2,09 < tтабл.
=2,36
Следовательно, свойство независимости остатков выполняется.
4) С помощью функции СТАНДОТКЛОН Мастера функций Excel по таблице 3.6 найдем среднее квадратическое отклонение.
Sε
= 0,92
Определим RS-критерий:
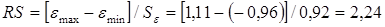
Расчетное значение попадает между табулированными границами (2,7-3,7) (для п=9 и 5-% уровня значимости), значит, остатки следуют нормальному закону распределения.
Модель в целом адекватна.
4. Оценим точность модели на основе использования средней относительной ошибки аппроксимации. Для этого рассчитаем в Excel следующую таблицу:
Таблица 3.7
| Точность
|
| yt
, факт. |
abs остатков |
Расчет Еотн |
| 8 |
0,02 |
0,002778 |
| 13 |
1,01 |
0,077778 |
| 15 |
0,96 |
0,063704 |
| 19 |
0,92 |
0,048538 |
| 25 |
1,11 |
0,044444 |
| 27 |
0,86 |
0,031687 |
| 33 |
1,18 |
0,03569 |
| 35 |
0,79 |
0,02254 |
| 40 |
0,24 |
0,006111 |
| Еотн =
|
3,70% |
Чтобы рассчитать вторую колонку воспользуемся функцией ABS Мастера функций Excel. Затем рассчитаем среднюю относительную ошибку аппроксимации:.
Еотн
= 3,70 %
Отсюда вывод: модель высокой точности и пригодна для целей прогнозирования.
5. Прогноз спроса на кредитные ресурсы на следующие две недели.
1) Рассчитаем среднее значение фактора «время» (tср
) и сумму квадратов отклонений t от его средней величины ( ∑(t-tср
)2
).
Таблица 3.8
| t |
yt, факт. |
t - tср |
| 1 |
8 |
-4 |
| 2 |
13 |
-3 |
| 3 |
15 |
-2 |
| 4 |
19 |
-1 |
| 5 |
25 |
0 |
| 6 |
27 |
1 |
| 7 |
33 |
2 |
| 8 |
35 |
3 |
| 9 |
40 |
4 |
| 5 |
60 |
| tср
|
∑(t-tср
)2
|
2) Произведем точечный и интервальный прогнозы на 2 шага вперед.
| Шаг прогноза к=1 |
t - статистика |
1,12 |
Se
=0,99 |
Y(t) = 4,06 + 3,97t
Y(10) = 4,06 + 3,97*10 = 43,76
Y(11) = 4,06 + 3,97*11 = 47,73
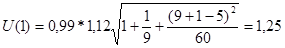
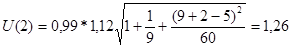
В результате расчетов получим следующую таблицу:
Таблица 3.9
| Время t |
Шаг k |
Прогноз |
Нижняя граница |
Верхняя граница |
| 10 |
1 |
43,76 |
42,51 |
45,01 |
| 11 |
2 |
47,73 |
46,47 |
48,99 |
По полученным данным построим график подбора: 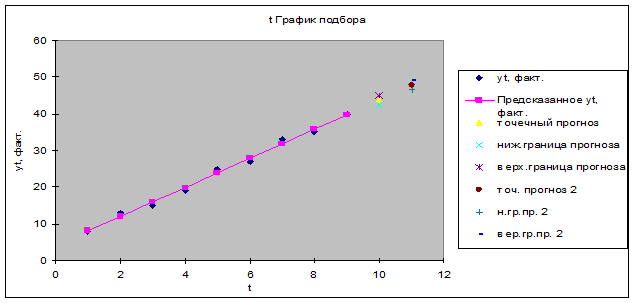
Таким образом, с вероятностью прогноза 70% можно утверждать, что значение спроса на кредитные ресурсы в течение следующих двух недель будет находиться в интервале 42,51 - 45,01 и 46,47 – 48,99 соответственно.
Список литературы
1. Федосеев В.В., Гармаш А.Н., Орлова И.В., Половников В.А. Экономико-математические методы и прикладные модели. 2-е изд. – М.: ЮНИТИ-ДАНА, 2005.
2. Половников В.А., Орлова И.В., Гармаш А.Н. Экономико - математические методы и прикладные модели: Методические указания по выполнению контрольной работы, темы и задачи. – М.: ВЗФЭИ, 2002.
3. Гармаш А.Н., Гусарова О.М., Орлова И.В., Якушев А.А. Экономико-математические методы и прикладные модели: Компьютерный практикум и руководство к выполнению лабораторной работы по теме «Оптимизационные экономико-математические модели. Методы получения оптимальных решений». – М.: ВЗФЭИ, 2002.
4. Орлова И.В. Экономико-математическое моделирование. Практическое пособие по решению задач. – М.: ВЗФЭИ: Вузовский учебник, 2004.
5. Орлова И.В. Экономико-математические методы и модели. Выполнение расчетов в среде Excel: Практикум. – М.: Финстатинформ. 2000.
|