Теорема Котельникова.
Для того, чтобы восстановить исходный непрерывный сигнал из дискретизированного с малыми искажениями (погрешностями), необходимо рационально выбрать шаг дискретизации. Поэтому при преобразовании аналогового сигнала в дискретный обязательно возникает вопрос о величине шага дискретизации 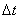 . Интуитивно нетрудно понять следующую идею. Если аналоговый сигнал обладает низкочастотным спектром, ограниченным некоторой верхней частотой Fe
, (т.е. функция u(t)
имеет вид плавно изменяющейся кривой, без резких изменений амплитуды), то вряд ли на некотором небольшом временном интервале дискретизации . Интуитивно нетрудно понять следующую идею. Если аналоговый сигнал обладает низкочастотным спектром, ограниченным некоторой верхней частотой Fe
, (т.е. функция u(t)
имеет вид плавно изменяющейся кривой, без резких изменений амплитуды), то вряд ли на некотором небольшом временном интервале дискретизации 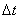 эта функция может существенно изменяться по амплитуде. эта функция может существенно изменяться по амплитуде.
Совершенно очевидно, что точность восстановления аналогового сигнала по последовательности его отсчетов зависит от величины интервала дискретизации 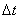 . Чем он короче, тем меньше будет отличаться функция u(t) от плавной кривой, проходящей через точки отсчетов. Однако с уменьшением интервала дискретизации . Чем он короче, тем меньше будет отличаться функция u(t) от плавной кривой, проходящей через точки отсчетов. Однако с уменьшением интервала дискретизации 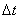 существенно возрастает сложность и объем обрабатывающей аппаратуры. При достаточно большом интервале дискретизации существенно возрастает сложность и объем обрабатывающей аппаратуры. При достаточно большом интервале дискретизации 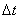 возрастает вероятность искажения или потери информации при восстановлении аналогового сигнала. возрастает вероятность искажения или потери информации при восстановлении аналогового сигнала.
Оптимальная величина интервала дискретизации устанавливается теоремой Котельникова (другие названия — теорема отсчетов, теорема К. Шеннона, теорема X. Найквиста: впервые теорема была открыта в математике О. Коши, а затем описана повторно Д. Карсоном и Р. Хартли), доказанной им в 1933 г. Теорема В. А. Котельникова имеет важное теоретическое и практическое значение: дает возможность правильно осуществить дискретизацию аналогового сигнала и определяет оптимальный способ его восстановления на приемном конце по отсчетным значениям.
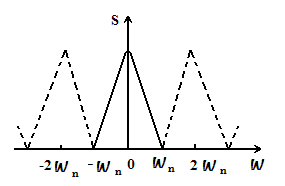
Рис.14.1. Представление спектральной плотности
Согласно одной из наиболее известных и простых интерпретаций теоремы Котельникова, произвольный сигнал u(t), спектр которого ограничен некоторой частотой Fe
может - быть полностью восстановлен по последовательности своих отсчетных значений, следующих с интервалом времени
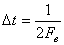 (1) (1)
Интервал дискретизации 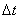 и частоту Fe
(1) в радиотехнике часто называют соответственно интервалом и частотой Найквиста. Аналитически теорема Котельникова представляется рядом и частоту Fe
(1) в радиотехнике часто называют соответственно интервалом и частотой Найквиста. Аналитически теорема Котельникова представляется рядом
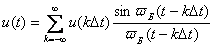 (2) (2)
где k — номер отсчета;  — значение сигнала в точках отсчета; — значение сигнала в точках отсчета; 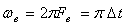 — верхняя частота спектра сигнала. — верхняя частота спектра сигнала.
Для доказательства теоремы Котельникова рассмотрим произвольный непрерывный сигнал и(t), спектральная плотность  которого сосредоточена в полосе частот которого сосредоточена в полосе частот 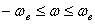 (сплошная линия на рис.14.1). (сплошная линия на рис.14.1).
Мысленно дополним график спектральной плотности 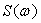 симметрично значениям, повторяющимся с периодом симметрично значениям, повторяющимся с периодом 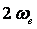 , (штриховые линии на рис.14.1). Полученную таким образом периодическую функцию разложим в ряд Фурье, заменив в формуле , (штриховые линии на рис.14.1). Полученную таким образом периодическую функцию разложим в ряд Фурье, заменив в формуле
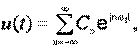
аргумент t
на с 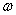 , частоту , частоту 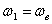 на на 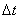 и (формально) п
на k
. Тогда и (формально) п
на k
. Тогда
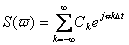 (3) (3)
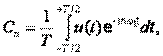
период — это 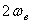 , а интервал дискретизации , а интервал дискретизации 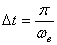 запишем запишем
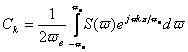 (4) (4)
Воспользуемся формулой обратного преобразования Фурье и представим исходный непрерывный сигнал в следующем виде:
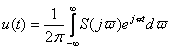 (5) (5)
Таким же образом запишем значение дискретизированного сигнала для некоторого k-то отсчета времени. Поскольку время 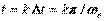 , то , то
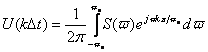
Сравнив это выражение с формулой для Ck
, замечаем, что 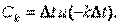 С учетом этого соотношения спектральная функция (3), после несложных преобразований, примет вид: С учетом этого соотношения спектральная функция (3), после несложных преобразований, примет вид:
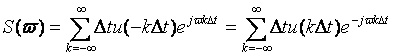 (7) (7)
Затем проделаем следующее: подставим выражение 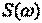 в соотношение в соотношение  , изменим порядок интегрирования и суммирования, представим отношение как , изменим порядок интегрирования и суммирования, представим отношение как 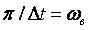 , и вычислим интеграл. , и вычислим интеграл.
В результате получим такую формулу:
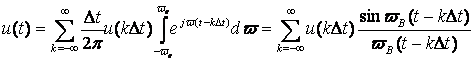
Из этого соотношения следует, что непрерывная функция u(t) действительно определяется совокупностью ее дискретных значений амплитуды в отсчетные моменты времени 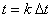 , что и доказывает теорему Котельникова. , что и доказывает теорему Котельникова.
Простейшие сигналы вида 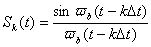 ортогональные друг другу на интервале времени - ортогональные друг другу на интервале времени - , ,  , называются функциями отсчетов, базисными функциями, или функциями Котельникова. График k-й функции Котельникова представлен на рис. 2. Каждая из базисных функций sk
(t)
сдвинута относительно подобной ближайшей функции sk-1
(t)
или sk+1
(t)
на интервал дискретизации , называются функциями отсчетов, базисными функциями, или функциями Котельникова. График k-й функции Котельникова представлен на рис. 2. Каждая из базисных функций sk
(t)
сдвинута относительно подобной ближайшей функции sk-1
(t)
или sk+1
(t)
на интервал дискретизации 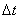 . Элементарный анализ формулы (10) и графика на рис. 14.3 показывает, что сигнал sk
(t)
отражается . Элементарный анализ формулы (10) и графика на рис. 14.3 показывает, что сигнал sk
(t)
отражается
Реклама

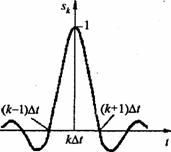
Рис. 14.2. График базисной функции Котельникова
Рис.14.3. Аппроксимация непрерывного сигнала рядом Котельникова функцией sinx/x, которая также характеризует огибающую спектральной плотности прямоугольного импульса.
Представление (точнее, аппроксимация) заданного непрерывного сигнала u(t) рядом Котельникова (2) иллюстрируется диаграммами на рис. 14.3. графике (здесь базисные функции для упрощения показаны без аргумента t
построены четыре первых члена ряда, соответствующие отсчетам сигнала в моменты времени 0, 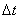 , 2 , 2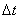 и 3 и 3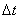 , взятым в соответствии с теоремой Котельникова. При суммировании этих членов ряда в любые отсчетные моменты времени kDt, непрерывный сигнал абсолютно точно аппроксимируется независимо от числа выбранных отсчетов. В интервале же между любыми отсчетами сигнал u(t) аппроксимируется тем точнее, чем больше суммируется членов ряда Котельникова (2). , взятым в соответствии с теоремой Котельникова. При суммировании этих членов ряда в любые отсчетные моменты времени kDt, непрерывный сигнал абсолютно точно аппроксимируется независимо от числа выбранных отсчетов. В интервале же между любыми отсчетами сигнал u(t) аппроксимируется тем точнее, чем больше суммируется членов ряда Котельникова (2).
Оценим возможность применения теоремы Котельникова к импульсному сигналу u(t) конечной длительности Tх
. Как известно, такие сигналы теоретически обладают бесконечно широким спектром. Однако на практике можно ограничиться некоторой верхней частотой Fв
за пределами которой в спектре содержится пренебрежительно малая доля энергии по сравнению с энергией всего исходного сигнала. В радиотехнике таким критерием является содержание 90% средней мощности сигнала в границах спектра. В этом случае сигнал u(t) длительностью Tх
с верхней граничной частотой спектра Fв
может быть представлен рядом Котельникова с определенным, ограниченным числом отсчетов
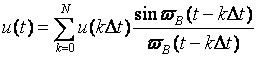 (10) (10)
Здесь 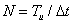 — число отсчетов. — число отсчетов.
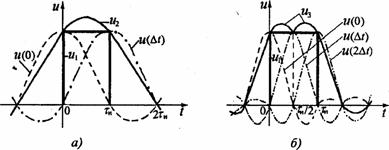
Рис.14.4. Представление прямоугольного импульса отсчетами:
о—двумя; б—тремя
|