| Экстремумы функции
На рисунке 123 изображён график функции y=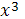 -3 -3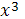 . Рассмотри окрестности точки
x
=0
, т.е. некоторый интервал содержащий эту точку. Как видно из рисунка, существует такая окрестность точки x
=0
, что наибольшее значение функция . Рассмотри окрестности точки
x
=0
, т.е. некоторый интервал содержащий эту точку. Как видно из рисунка, существует такая окрестность точки x
=0
, что наибольшее значение функция 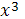 -3 -3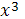 в этой окрестности принимает в точке x
= 0.
Например, на интервале (—1; 1) наибольшее значение, равное 0, функция принимает в точке x
=0.
Точку x
= 0
называют точкой максимума этой функции. в этой окрестности принимает в точке x
= 0.
Например, на интервале (—1; 1) наибольшее значение, равное 0, функция принимает в точке x
=0.
Точку x
= 0
называют точкой максимума этой функции.
Аналогично точку x
= 2
называют точкой минимума функции x
—Зх2
, так как значение функции в этой точке меньше ее значения в любой точке некоторой окрестности точки x
=2,
например окрестности (1,5; 2,5).
Точка 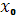 называется точкой максимума функции
(x
), если существует такая окрестность точки называется точкой максимума функции
(x
), если существует такая окрестность точки 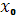 , что для всех x , что для всех x
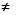 х0
из этой окрестности выполняется неравенство х0
из этой окрестности выполняется неравенство
f(x) 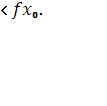
Например, точка хо
= 0 является точкой максимума функции f
(
x
)
=1—х2
, так как f
(0)=1
и при всех значениях x
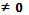 верно неравенство f
(
x
)
<1 (рис. 124). верно неравенство f
(
x
)
<1 (рис. 124).
Точка х0
называется точкой минимума функции
f(x),
если существует такая окрестность точки х0
,
что для всех x
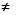 х0
из этой окрестности выполняется неравенство х0
из этой окрестности выполняется неравенство
f(x) 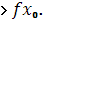
Например, точка х0
=2
является точкой минимума функции f(x) =3+(x— 2)2
, так как /(2) = 3 и /(х)>3 при всех значениях хф2
(рис. 125).
Точки минимума и точки максимума называются точка
ми экстремума.
Рассмотрим функцию /(х), которая определена в некоторой окрестности точки х0
и имеет производную в этой точке.
Теорема. Если х0
— точка экстремума дифференцируемой функции /(х), то /'(х0
) = 0.
Это утверждение называют теоремой Ферма1
.
Теорема Ферма имеет наглядный геометрический смысл: касательная к графику функции г/ = /(х) в точке (х0
; / (х0
), где х0
— точка экстремума функции г/ = /(х), параллельна оси абсцисс, и поэтому ее угловой коэффициент /'(х0
) равен нулю (рис. 126). Например, функция / (х) = 1 — х2
(рис. 124) имеет
|