НЕПАРАМЕТРИЧНІ МЕТОДИ ОЦІНКИ ТІСНОТИ ЗВ`ЯЗКУ
План
1. Критерії Спірмена та Кендала
2. Критерій Фехнера
3. Коефіцієнти асоціації і контингенції
4. Коефіцієнт взаємної спряженості Пірсона і Чупрова
Література
Серед непараметричних (емпіричних) методів оцінки тісноти зв’язку найбільше значення мають розрахунки рангових коефіцієнтів Спірмена 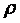 і Кендала і Кендала 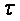 . .
Ці коефіцієнти можуть бути використанні для визначення тісноти зв’язку як між кількісними, так і між якісними ознаками при умові, якщо значення цих показників можуть бути впорядковані або проранговані по спаданню або зростанню ознаки.
Для визначення рангового коефіцієнта кореляції рангують (тобто записують у зростаючому або спадаючому порядку) всі значення факторної ознаки 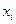 і разом з тим записують відповідні значення результативної ознаки і разом з тим записують відповідні значення результативної ознаки 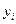 . Другими словами, визначають ранг по обох ознаках, тобто номер кожної ознаки в рангових рядах. . Другими словами, визначають ранг по обох ознаках, тобто номер кожної ознаки в рангових рядах.
Ступінь тісноти зв’язку між ознаками визначається ранговим коефіцієнтом кореляції Спірмена по формулі:

де 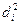 - квадрати різниць рангів зв’язаних величин - квадрати різниць рангів зв’язаних величин 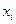 і і 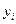 ; п -
число спостережень (число пар рангів). ; п -
число спостережень (число пар рангів).
У випадку відсутності зв’язку 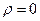 ; при прямому зв’язку коефіцієнт ; при прямому зв’язку коефіцієнт 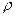 додатній, а при оберненому зв’язку - від’ємний. додатній, а при оберненому зв’язку - від’ємний.
Приклад 1.
Визначити, чи існує залежність між стажем роботи та виробітком робітника для слідуючих даних:
Таблиця 1
| № п/п |
Стаж роботи робітників, х, роки
|
Виробіток на 1 робітника, у
|
| 1 |
2,5 |
222 |
| 2 |
2,5 |
223 |
| 3 |
1 |
200 |
| 4 |
1 |
202 |
| 5 |
1 |
205 |
| 6 |
5 |
244 |
| 7 |
5 |
250 |
| 8 |
3 |
234 |
| 9 |
4,5 |
241 |
| 10 |
4,4 |
244 |
| 11 |
2,7 |
230 |
Рішення.
Фактори 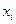 і і 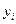 ранжуємо (впорядкуємо) в порядку зростання (спадання) їх значень і заповнюємо табл. 2. ранжуємо (впорядкуємо) в порядку зростання (спадання) їх значень і заповнюємо табл. 2.
Таблиця 2
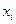 |
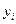 |
Ранг ознаки х
|
Ранг ознаки у
|
Рангова різниця |
 |
| 1 |
200 |
4 |
3 |
1 |
1 |
| 1 |
202 |
4 |
4 |
0 |
0 |
| 1 |
205 |
4 |
5 |
-1 |
1 |
| 2,5 |
222 |
1,5 |
1 |
0,5 |
0,25 |
| 2,5 |
223 |
1,5 |
2 |
-0,5 |
0,25 |
| 2,7 |
230 |
11 |
11 |
0 |
0 |
| 3 |
234 |
8 |
8 |
0 |
0 |
| 4,4 |
241 |
10 |
9 |
1 |
1 |
| 4,5 |
244 |
9 |
8 |
1 |
1 |
| 5 |
244 |
6,5 |
8 |
-1,5 |
2,25 |
| 5 |
250 |
6,5 |
7 |
-0,5 |
0,25 |
| Всього |
3,5-3,5=0 |
7 |
Визначаємо ранги по обох ознаках, тобто номер кожної ознаки в рангованих рядах. Для рівних значень факторів х
та у
ранг знаходять шляхом ділення суми рангів, що приходяться на неї, на число рівних значень.
3. Знаходимо рангову різницю 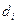 та та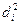 . .
4. Розрахуємо коефіцієнт кореляції рангів Спірмена:

Розрахунок рангового коефіцієнта Кендала відбувається за формулою:
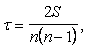
де п
- число спостережень; S
- сума додатних та від’ємних балів по одній із зв’язаних величин, ранги котрої розміщені у відповідності з впорядкованими рангами другої.
2.
Критерій Фехнера
Одним із найпростіших показників кореляційної залежності, пов’язаний з іменем відомого німецького вченого психофізика Фехнера.
Коефіцієнт Фехнера базується на застосуванні перших ступенів відхилень всіх значень взаємозв’язаних ознак від середньої величини по кожній ознаці.
Реклама

Коефіцієнт Фехнера вимірює тісноту зв’язку за наступною формулою:
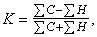
де 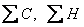 - число збігів та незбігів знаків відхилень значень фактичної і результативної ознак від своїх середніх, тобто - число збігів та незбігів знаків відхилень значень фактичної і результативної ознак від своїх середніх, тобто 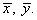 При цьому фіксуються збіги та незбіги знаків в відхиленнях від середньої у
різних пар значень ознак. При цьому фіксуються збіги та незбіги знаків в відхиленнях від середньої у
різних пар значень ознак.
Коефіцієнт Фехнера К
змінюється в межах від - 1 до +1. Якщо зв’язок між ознаками обернений, то К
від’ємний; у випадку прямого зв’язку - додатній. Чим ближче К
до 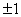 , тим зв’язок більш тісний. , тим зв’язок більш тісний.
Приклад 2.
Розрахувати коефіцієнт Фехнера для наступних даних:
Таблиця 3
| Стаж роботи, х
|
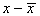 |
Виробіток на 1 робітника, у
|
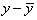 |
Збіг чи незбіг знаків |
| 2,5 |
- |
222 |
- |
С |
| 2,5 |
- |
223 |
- |
С |
| 1 |
- |
200 |
- |
С |
| 1 |
- |
202 |
- |
С |
| 1 |
- |
205 |
- |
С |
| 5 |
+ |
244 |
+ |
С |
| 5 |
+ |
250 |
+ |
С |
| 3 |
+ |
234 |
+ |
С |
| 4,5 |
+ |
241 |
+ |
С |
| 4,5 |
+ |
244 |
+ |
С |
| 2,7 |
- |
230 |
+ |
Н |
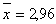 |
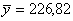 |
Коефіцієнт Фехнера
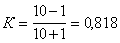
Величина К
досить близька до величини коефіцієнта рангової кореляції Спірмена, що свідчить про тісний зв’язок між ознаками х
і у
.
3.
Коефіцієнти асоціації і контингенції
Для визначення тісноти зв’язку двох якісних ознак, кожна із котрих складається тільки із двох груп, використовують коефіцієнти асоціації і контингенції. Для їх розрахунку будується чотирьохклітинна таблиця кореляції, котра виражає зв’язок між двома явищами, кожне із них в свою чергу повинно бути альтернативним, тобто складається із двох якісно відмінних друг від друга значень ознаки (наприклад, хороший, поганий).
Наприклад, при вивчені залежності врожайності від кількості внесених в ґрунт добрив виділимо по врожайності і по кількості внесених добрив лише по дві групи. При цій умові можна побудувати наступну чотирьохклітинну таблицю.
Таблиця 4
Удобрено
Урожайність
|
Добре |
Погано |
Всього |
| Висока |
а
|
в
|
a+b
|
| Низька |
с
|
d
|
c+d
|
| Всього |
а+c
|
b+d
|
Числа, які стоять на перетині рядків і граф a, в, c, d
показують, скільки дільниць зустрічаються з тою або другою кількістю добрив, що внесені в ґрунт, з тією або другою врожайністю.
Коефіцієнт асоціації Юла і коефіцієнт контингенції розраховується за наступними формулами:
асоціації Юла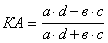 ; ;
контингенції 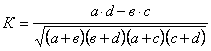 . .
де a, в, c, d
-
кількісні характеристики досліджувальних груп.
Коефіцієнт контингенції завжди менший коефіцієнта асоціації Юла. Зв’язок рахується підтвердженим, якщо:
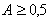 або або 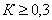 . .
Приклад 3.
Дослідити зв’язок між виконанням норм виробітку молодими робітниками і закінченням ними середньої школи. Результати обстеження характеризуються даними (табл. 5).
Таблиця 5
| Групи робітників |
Виконують норму |
Не виконують норму |
Всього |
| Закінчили середню школу |
78 |
22 |
100 |
| Не закінчили середню школу |
32 |
68 |
100 |
| Всього |
110 |
90 |
200 |
Рішення.
За даними таблиці
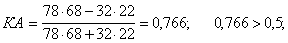
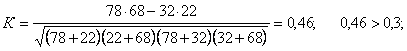
Між досліджувальними ознаками спостерігається чіткий зв’язок, що підтверджується досить високими значеннями коефіцієнтів асоціації і контингенції.
Якщо кожна із якісних ознак складається більше ніж із двох груп, то для визначення тісноти зв’язку можна використати коефіцієнт взаємної спряженості Пірсона. Цей коефіцієнт розраховується за наступною формулою:
Реклама

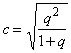
де q2
- показник взаємної спряженості.
Коефіцієнт Чупрова:
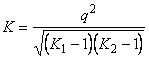 , ,
де К1
, К2
- число груп по кожній із ознак.
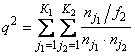
Розрахунок коефіцієнта взаємної спряженості проводиться за наступною схемою (табл. 6).
Таблиця 6
| Групи ознаки А |
Групи ознак В |
Разом |
| В1
|
В2
|
В3
|
| А1
|
f1
|
f2
|
f3
|
n1
|
| A2
|
f4
|
f5
|
f6
|
n2
|
| A3
|
f7
|
f8
|
f9
|
n3
|
| Разом |
т1
|
т2
|
т3
|
Розрахунок q2
:
по першому рядку
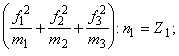
по другому рядку
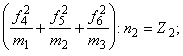
по третьому рядку
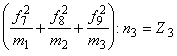
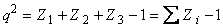 . .
Приклад 4.
В таблиці 2.7 приведені згруповані дані накладних видатків (х
) та собівартості продукції (у
). За допомогою коефіцієнта взаємної спряженості дослідити зв’язок між собівартістю продукції та накладними витратами на реалізацію.
Рішення.
Розрахуємо q2
:
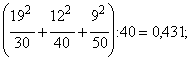
по першому рядку 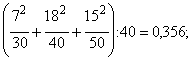
Таблиця 2.7
| Накладні |
Собівартість |
Разом |
| витрати |
нижня |
середня |
висока |
| Нижні |
19 |
12 |
9 |
40 |
| Середні |
7 |
18 |
15 |
40 |
| Високі |
4 |
10 |
26 |
40 |
| Разом |
30 |
40 |
50 |
по другому рядку 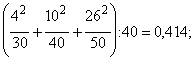
по третьому рядку
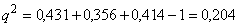 . .
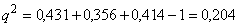 . .
Підставляємо 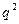 у відповідні формули і знаходимо: у відповідні формули і знаходимо:
коефіцієнт Пірсона: 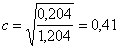 , ,
коефіцієнт Чупрова: 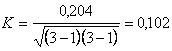 . .
Досить високе значення с
вказує на наявність зв’язку між собівартістю продукції та накладними витратами на реалізацію.
Непараметричні методи вимірювання зв’язку використовуються для перевірки умов використання метода найменших квадратів, незалежності розподілу ознак, однорідності вибірок, наявності тренда в рядах динаміки.
1. Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики.М., ЮНИТИ. 1998 - 1022 с.
2. Ликеш И., Ляга Й. Основные таблицы математической статистики. - М. "Финансы и статистика", 1985. - 356 с.
3. Доугерти Кристофер. Введение в эконометрику.
Пер. с англ. - М., ИНФРА-М. - XIV. 1997 - 402 c.
4. Maddala G.L., Kim In-Moo Unit Roots, Cointegration, and Structural Change
. Cambridge Univ. Press., 1999.
5. Davidson R., MacKinnon J.G. Estimation and Inference in Econometrics
. Oxford Univ. Press., 1993.
|