Проверка адекватности выбранных моделей
Проверка адекватности выбранных моделей реальному процессу ( в частности, адекватности полученной кривой роста) строится на анализе случайной компоненты. Случайная остаточная компонента получается после выделения из исследуемого ряда систематической составляющей (тренда и периодической составляющей, если она присутствует во временном ряду). Предположим, что исходный временной ряд описывает процесс, не подверженный сезонным колебаниям, т.е. примем гипотезу об аддитивной модели ряда вида:
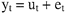 (1) (1)
Тогда ряд остатков будет получен как отклонения фактических уровней временного ряда (yt
) от выравненных, расчетных (ŷ
t
):
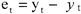 (2) (2)
При использовании кривых роста ŷt
вычисляют, подставляя в уравнения выбранных кривых соответствующие последовательные значения времени.
Принято считать, что модель адекватна описываемому процессу, если значения остаточной компоненты удовлетворяют свойствам случайности, независимости, а также случайная компонента подчиняется нормальному закону распределения.
При правильном выборе вида тренда отклонения от него будут носить случайный характер. Это означает, что изменение остаточной случайной величины не связано с изменением времени. Таким образом, по выборке, полученной для всех моментов времени на изучаемом интервале, проверяется гипотеза о зависимости последовательности значений et
от времени, или, что то же самое, о наличии тенденции в ее изменении. Поэтому для проверки данного свойства может быть использован один из критериев, рассматриваемых в разделе 1, например, критерий серий.
Если вид функции, описывающей систематическую составляющую, выбран неудачно, то последовательные значения ряда остатков могут не обладать свойствами независимости, т.к. они могут коррелировать между собой. В этом случае говорят, что имеет место автокорреляция ошибок.
В условиях автокорреляции оценки параметров модели, полученные по методу наименьших квадратов, будут обладать свойствами несмещенности и состоятельности (с этими свойствами знакомятся в курсе математической статистики). В то же время эффективность этих оценок будет снижаться, а, следовательно, доверительные интервалы будут иметь мало смысла в силу своей ненадежности.
Реклама

Существует несколько приемов обнаружения авто корреляции. Наиболее распространенным является метод, предложенный Дарбиным и Уотсоном. Критерий Дарбина-Уотсона связан с гипотезой о существовании автокорреляции первого порядка, Т.е. автокорреляции между соседними остаточными членами ряда. Значение этого критерия определяется по формуле:
d = 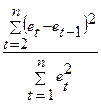 (3) (3)
Можно показать, что величина d приближенно равна:
d≈ 2(1-r1
)
где r1
- коэффициент автокорреляции первого порядка (т.е. парный коэффициент корреляции между двумя рядами е1
, е2
, ... ,еn
-1
и е2
, е3
,…,en
).
Из последней формулы видно, что если в значениях et
имеется сильная положительная авто корреляция ( r1
≈1), то величина d=0, в случае сильной отрицательной автокорреляции (r1
≈-1) d=4. При отсутствии автокорреляции (r≈0) d=2.
Для этого критерия найдены критические границы, позволяющие принять или отвергнуть гипотезу об отсутствии автокорреляции. Авторами критерия границы определены для 1; 2,5; и 5% уровней значимости. Значения критерия Дарбина- Уотсона при 5% уровне значимости приведены в таблице. В этой таблице d1
и d2
– соответственно нижняя и верхняя доверительные границы критерия Дарбина- Уотсона; k1
– число переменных в модели; n- длина ряда.
Таблица.
Значение критерия Дарбина- Уотсона d1
и d2
при 5% уровне значимости
| n |
K1
=1 |
K1
=2 |
K1
=2 |
| d1
|
d2
|
d1
|
d2
|
d1
|
d2
|
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
1.08
1.1
1.13
1.16
1.18
1.2
1.22
1.24
1.26
1.27
1.29
1.3
1.32
1.33
1.34
1.35
1.36
1.37
1.38
1.49
1.4
1.41
|
1.36
1.37
1.38
1.39
1.4
1.41
1.42
1.43
1.44
1.45
1.45
1.46
1.47
1.48
1.48
1.49
1.5
1.5
1.51
1.51
1.52
1.52
|
0.95
0.98
1.02
1.05
1.08
1.1
1.13
1.15
1.17
1.19
1.21
1.22
1.24
1.26
1.27
1.28
1.3
1.31
1.32
1.33
1.34
1.35
|
1.54
1.54
1.54
1.53
1.53
1.54
1.54
1.54
1.54
1.55
1.55
1.55
1.56
1.56
1.56
1.57
1.57
1.57
1.58
1.58
1.58
1.59
|
0.82
0.86
0.9
093
0.97
1
1.03
1.05
1.08
1.1
1.12
1.14
1.16
1.18
1.2
1.21
1.23
1.24
1.26
1.27
1.28
1.29
|
1.75
1.73
1.71
1.69
1.68
1.68
1.67
1.66
1.66
1.66
1.66
1.65
1.65
1.65
1.65
1.65
1.65
1.65
1.65
1.65
1.65
1.65
|
Применение на практике критерия Дарбина- Уотсона основано на сравнении величины d, рассчитанной по формуле (3), с теоретическими значениями d1
иd2
, взятыми из таблицы. Отметим, что большинство программных пакетов статистической обработки данных осуществляет расчет этого критерия (например, ППП "Олимп", "Мезозавр", "Statistica" и др.).
При сравнеии величины d с d1
и d2
возможны следующие варианты:
1) Если d<d1,
то гипотеза о независимости случайных отклонений (отсутствие автокорреляции) отвергается;
Реклама

2) Если d>d2
, то гипотеза о независимости случайных отклонений не отвергается;
3) Если d1
≤d≤d2
, то нет достаточных оснований для принятия решений, т.е. величина попадает в область "неопределенности" .
Рассмотренные варианты относятся к случаю, когда в остатках имеется положительная автокорреляция.
Когда же расчетное значение d превышает 2, то можно говорить о том, что в et
существует отрицательная автокорреляция.
Для проверки отрицательной автокорреляции с критическими значениями dj
и d2
сравнивается не сам коэффициент d, а 4-d.
Для определения доверительных интервалов модели свойство
нормальности распределения остатков имеет важное значение. Поскольку временные ряды экономических показателей, как правило, невелики (<50), то проверка распределения на нормальность может быть произведена лишь приближенно, например, на основе исследования показателей асимметрии и эксцесса.
При нормальном распределении показатели асимметрии (А) и эксцесса (Э) равны нулю. Так как мы предполагаем, что отклонения от тренда представляют собой выборку из некоторой генеральной совокупности, то можно определить выборочные характеристики асимметрии и эксцесса, а также их среднеквадратические ошибки.
А=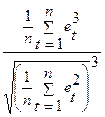 (4) (4)
Э=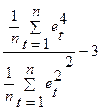 (5) (5)
σa
=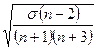 (7) (7)
где А- выборочная характеристика асимметрии;
Э- выборочная характеристика экцесса;
σА
- среднеквадратическая ошибка выборочной характеристики асимметрии;
σЭ
- среднеквадратическая ошибка выборочной характеристики экцесса.
Если одновременно выполняются следующие неравенства:
|А|<1,5σА
; | 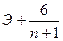 |<1,5σЭ
(8) |<1,5σЭ
(8)
то гипотеза о нормальном характере распределения случайной компоненты не отвергается.
Если выполняется хотя бы одно из неравенств
|А|≥2σА;
|Э+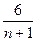 | ≥2σ (9) | ≥2σ (9)
то гипотеза о нормальном характере распределения отвергается.
Другие случаи требуют дополнительной проверки с помощью более мощных критериев.
Классификация прогнозов. Требования, предъявляемые к временным рядам, их компонентный состав
1. Изменения курса акций промышленной компании в течение месяца представлены в таблице:
курс акции (Дол.)
tYttYttYttYt
1 509 6 515 11 517 16 510
2 507 7 520 12 524 17 516
3 508 8 519 13 526 18 518
4 509 9 512 14 519 19 524
5 518 10 511 15 514 20 521
Проверить утверждение об отсутствии тенденции в изменении курса акций двумя способами:
а) с помощью метода Фостера - Стюарта;
б) используя критерий серии, основанный на медиане выборки. Доверительную вероятность принять равной 0,95.
2. Проверим гипотезу об отсутствии тенденции в изменении курса акций с помощью критерия серий, основанного на медиане выборки.
3. Годовые данные об изменении урожайности зерновых культу; представлены в таблице. С помощью критерия "восходящих и нисходящих" серий проверить утверждение о том, что в изменении урожайности имеется тенденция.
Урожайность зерновых культур (ц/га)
| t |
Yt
|
t |
Yt
|
t |
Yt
|
t |
Yt
|
| 1 |
6,7 |
6 |
8,6 |
11 |
8,4 |
16 |
9,1 |
| 2 |
7,3 |
7 |
7,8 |
12 |
9,1 |
17 |
9,5 |
| 3 |
7,6 |
8 |
7,7 |
13 |
8,3 |
18 |
10,4 |
| 4 |
7,9 |
9 |
7,9 |
14 |
8,7 |
19 |
10,5 |
| 5 |
7,4 |
10 |
8,2 |
15 |
8,9 |
20 |
10,2 |
| 21 |
9,3 |
Доверительную вероятность принять равной 0,95.
Решение
1. Вспомогательные вычисления по методу Фостера- Стюарта представлены в таблице 1.
1) Если уровень yt
больше всех предшествующих уровней, то в графе mt
ставим 1, если yt
меньше всех предшествующих уровней, то ставим 1 в графе lt
;
2) Определяем dt
=mt
-1t
для t=2ч20;
3) D = 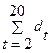 =3; =3;
4) Значение σd
для n=20 берем из таблицы 1.2.
σd
=2,279.
Значение tкp
берем из таблицы t- распределения Стьюдента:
tкp
(а=О,05; К=19)=2,093;
tH
=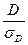 =
1,316. =
1,316.
TH
< Tk
р
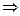 нет оснований отвергнуть гипотезу об отсутствии тренда. нет оснований отвергнуть гипотезу об отсутствии тренда.
С вероятностью 0,95 тренд во временном ряду отсутствует.
Вспомогательные вычисления представлены в таблице 1.4.
Таблица 1
Вспомогательные вычисления по методу Фостера- Стюарта
| t |
Yt
|
Mt
|
Et
|
Dt
|
t |
Yt
|
Mt
|
Et
|
Dt
|
1
2
3
4
5
6
7
8
9
10
|
509
507
508
509
518
515
520
519
512
511
|
-
0
0
0
1
0
1
0
0
0
|
-
1
0
0
0
0
0
0
0
0
|
-
-1
0
0
1
0
1
0
0
0
|
11
12
13
14
15
16
17
18
19
20
|
517
524
526
519
514
510
516
518
524
521
|
0
1
1
0
0
0
0
0
0
0
|
0
0
0
0
0
0
0
0
0
0
|
0
1
1
0
0
0
0
0
0
0
|
Вспомогательные вычисления представлены в таблице 2
| t |
Yt
|
Y'
t
|
t |
Yt
|
Y'
t
|
t |
Yt
|
Y'
t
|
1
2
3
4
5
6
|
509
507
508
509
518
515
|
507
508
509
509
510
511
|
-
-
-
-
+
-
|
7
8
9
10
11
12
13
14
|
520
519
512
511
517
524
526
519
|
512
514
515
516
517
518
518
519
|
+
+
-
-
+
+
+
+
|
15
16
17
18
19
20
|
519
520
521
524
524
526
|
519
520
521
524
524
526
|
-
-
-
+
+
+
|
1) от исходного ряда yt
переходим к ранжированному yt
'
, расположив значения исходного ряда в порядке возрастания;
2) Т.к. n=20 (четное) 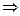
Медиана
Ме
= 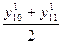 =516,5; =516,5;
3) Значение каждого уровня исходного ряда yt
сравнивается со значением медианы. Если yt
>Ме
, то δi
принимает значение «+», если меньше, то «-»;
4) v (20)=8- число серий;
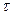 max
(20)=4- протяженность самой большой серии. max
(20)=4- протяженность самой большой серии.
В соответствии делаем проверку:
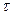 max
(20)<[3,3(lg20+1)] max
(20)<[3,3(lg20+1)]
v(20)>[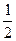 (20+1-1.96 (20+1-1.96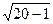 )] )]
4<7
8>6
Оба неравенства выполняются. С вероятностью 0,95 тренд во временном ряду отсутствует, что согласуется с выводом, сделанным с помощью метода Фостера-Стюарта.
Таблица 3
| t |
Yt
|
t |
Yt
|
t |
Yt
|
1
2
3
4
5
6
|
6,7
7,3
7,6
7,9
7,4
8,6
|
+
+
+
-
+
|
7
8
9
10
11
12
|
7,8
7,7
7,9
8,2
8,4
9,1
|
-
-
+
+
+
+
|
13
14
15
16
17
18
19
20
21
|
8,3
8,7
8,9
9,1
9,5
10,4
10,5
10,2
9,3
|
-
+
+
+
+
+
+
-
-
|
Вспомогательные вычисления в задании
В графе δ ставим «+», если последующее значение уровня временного ряда больше предыдущего, «-» - если меньше. Определим v (21)=8 – число серий.
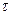 max
(21)=6 – протяженность самой большой серии. Табличное значение max
(21)=6 – протяженность самой большой серии. Табличное значение
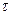 0
(21)=5. В соответствии делаем проверку: 0
(21)=5. В соответствии делаем проверку:
V(21)>[ 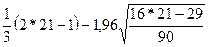 ] ]
max
(21)≤  0
(21) 0
(21)
8>10
6≤5
Т.к. оба неравенства не выполняются, то делаем выводы: во временном ряду урожайности имеется тенденции.
|