Российский государственный педагогический университет
имени А.И. Герцена

Кафедра прикладной математики
Лабораторная работа по исследованию функции в математическом пакете MathC
AD
.
Выполнила:
студентка 1 курса 2 группы
факультета физики
Потапова Вера
Проверили:
Матюшичев И.Ю. ______________
Свенцицкая Т.А. ______________
Санкт-Петербург
2010 г.
Оглавление:
1Исследование функции: 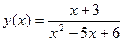 .............................. 3 .............................. 3
1.1Область определения:3
1.2Область допустимых значений:3
1.3Промежутки знака постоянства y > 0; y < 0, при каких x. Корни функции, точки пересечения с координатными осями.3
1.3.1 Промежутки знака постоянства: 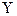 >0; Y<0. 3 >0; Y<0. 3
1.3.2 Точки пересечения с осями:3
1.4Исследование функции по первой производной. Экстремумы функции.3
1.5Исследование по второй производной. Точки перегиба.3
1.6Асимптоты графика.4
1.6.1Вертикальные асимптоты (точки в которых функция не определена):4
1.6.2Горизонтальные асимптоты:4
1.6.3Наклонные асимптоты:4
1.7График функции: 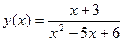 .............................. 4 .............................. 4
2Исследование функции: 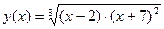 ........................................ 5 ........................................ 5
2.1Область определения:5
2.2Область допустимых значений:5
2.3Промежутки знака постоянства y > 0; y < 0, при каких x. Корни функции, точки пересечения с координатными осями.5
2.3.1Промежутки знака постоянства: 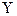 >0; Y<0. 5 >0; Y<0. 5
2.3.2Точки пересечения с осями. 5
2.4Исследование по первой производной. Экстремумы функции.5
2.5Исследование по второй производной. Точки перегиба.5
2.6Асимптоты графика:6
2.6.1Вертикальные асимптоты.. 6
2.6.2Горизонтальные асимптоты:6
2.6.3Наклонные асимптоты:6
2.7График функции: 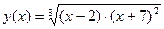 ........................................ 6 ........................................ 6
3График функции 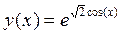 .............................. 7 .............................. 7
3.1Область определения:7
3.2Область допустимых значений:7
3.3Промежутки знака постоянства y > 0; y < 0, при каких x. Корни функции, точки пересечения с координатными осями.7
3.3.1Промежутки знака постоянства y > 0; y < 0. 7
3.3.2Точки пересечения с осями:7
3.4Исследование по первой производной. Экстремумы функции.7
3.5Исследование по второй производной. Точки перегиба. 8
3.6Асимптоты графика. 8
3.6.1Вертикальные асимптоты (точки в которых функция не определена)8
3.6.2Горизонтальные асимптоты.. 8
3.6.3Наклонные асимптоты.. 8
Реклама

3.7График функции: 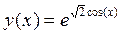 .............................. 8 .............................. 8
1 Исследование функции:
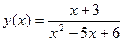
1.1 Область определения:
x ÎR.
1.2 Область допустимых значений:
y ÎR
1.3 Промежутки знака постоянства
y > 0; y < 0, при каких x. Корни функции, точки пересечения с координатными осями.
1.3.1 Промежутки знака постоянства: 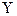 >0;
Y<0 >0;
Y<0
1.3.2 Точки пересечения с осями:
| OX |
OY |
Y=0
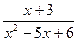 =0 =0
|
X=0
|
| А (-3; 0) |
А (0; 0.5) |
1.4 Исследование функции по первой производной. Экстремумы функции.
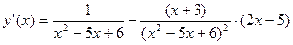
Точки минимума и максимума отсутствуют.
1.5 Исследование по второй производной. Точки перегиба.
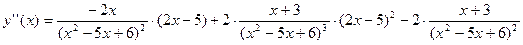
1.6 Асимптоты графика.
1.6.1 Вертикальные асимптоты (точки в которых функция не определена):
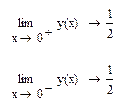
1.6.2 Горизонтальные асимптоты:
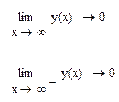
1.6.3 Наклонные асимптоты:
Наклонных асимптот нет.
1.7 График функции:
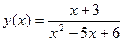
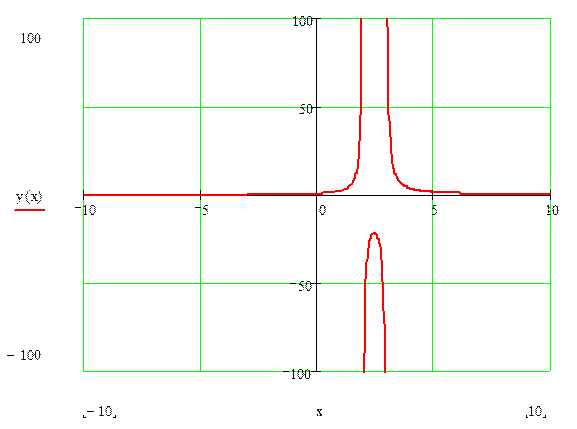
2 Исследование функции:
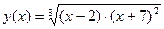
2.1 Область определения:
x ÎR
2.2 Область допустимых значений:
y ÎR
2.3 Промежутки знака постоянства
y > 0; y < 0, при каких x. Корни функции, точки пересечения с координатными осями.
2.3.1 Промежутки знака постоянства: 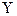 >0; Y<0 >0; Y<0
2.3.2 Точки пересечения с осями
| OX |
OY |
Y=0
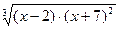 =0 =0
|
X=0
|
| нет точек пересечения
|
A (2; 0)
B(-7; 0)
|
2.4 Исследование по первой производной. Экстремумы функции.
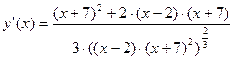
Точки минимума и максимума отсутствуют.
2.5 Исследование по второй производной. Точки перегиба.
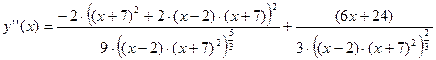
Точка перегиба: А (-1; -4.7622)
2.6 Асимптоты графика:
2.6.1 Вертикальные асимптоты
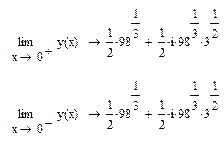
2.6.2 Горизонтальные асимптоты:
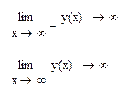
2.6.3 Наклонные асимптоты:
Наклонных асимптот нет.
2.7 График функции:
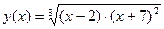
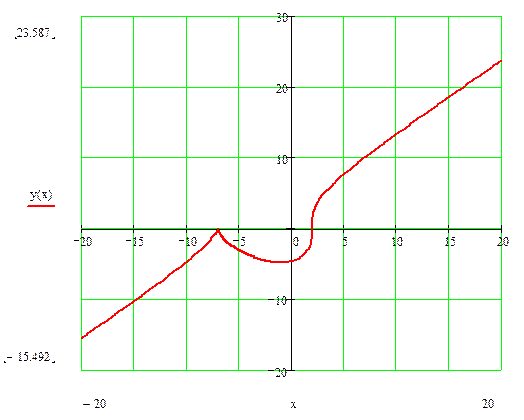
3 График функции
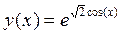
3.1 Область определения:
x ÎR
3.2 Область допустимых значений:
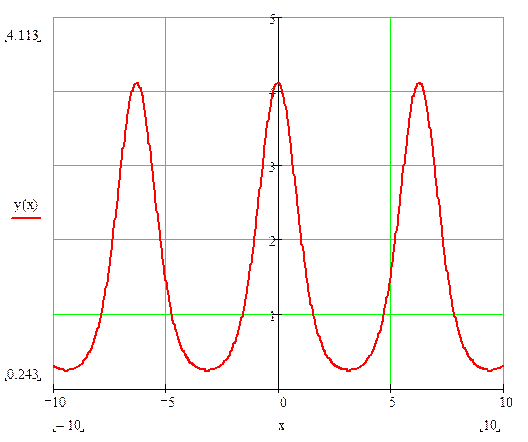
y Î [0.2431; 4.1132]
3.3 Промежутки знака постоянства
y > 0; y < 0, при каких x. Корни функции, точки пересечения с координатными осями.
3.3.1 Промежутки знака постоянства y > 0; y < 0
3.3.2 Точки пересечения с осями:
3.4 Исследование по первой производной. Экстремумы функции.
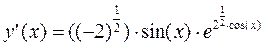
Экстремумы:
| OX |
OY |
min
max
min
max
min
max
|
-9.4200
-6.1100
-3.1400
0.0000
3.1400
6.1100
|
0.2431
4.1132
0.2431
4.1132
0.2431
4.1132
|
A (-6.1100; 4.1132); B (0.0000; 4.1132); C (6.1100; 4.1132) точки максимума
D (-9.4200; 0.2431); E (-3.1400; 0.2431); F (3.1400; 0.2431) точки минимума
3.5 Исследование по второй производной. Точки перегиба
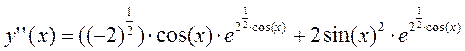
3.6 Асимптоты графика
3.6.1 Вертикальные асимптоты (точки в которых функция не определена)
Вертикальных асимптот нет, т.к. функция непрерывна на всей области определения.
3.6.2 Горизонтальные асимптоты
Горизонтальных асимптот нет
3.6.3 Наклонные асимптоты
Наклонных асимптот нет
3.7 График функции:
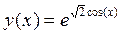
Реклама

|