| Министерство науки и образования Российской Федерации
Федеральное Агентство образования
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ЭКОНОМИКИ И УПРАВЛЕНИЯ - «НИХН»
Кафедра статистики
КУРСОВАЯ РАБОТА
По дисциплине: «Анализ временных рядов и прогнозирование»
Тема: «Эвристические методы периодизации»
Выполнила: _____________________________ студентка группы № БС-52
Корниченко Мария Алексеевна
Зачетная книжка № 051156
Проверила: ______________________________Глинский Владимир Васильевич
профессор к.э.н
Новосибирск 2007
Содержание
Введение . 3
1. Понятие периодизации, необходимость и возможность. 4
1.1 Сущность и условия временной периодизации. 4
1.2 Однородность временных рядов. 6
2. Эвристические методы периодизации. 7
2.1 Предварительные процедуры. 7
2.1 Вроцлавская таксономия: дендрит. 10
2.2 Метод шаров. 13
2.3 Метод корреляционных плеяд. 16
3. Периодизация здоровья в Российской Федерации за 1991- 2005 гг. 18
3.1 Предварительные процедуры. 18
3.2 Периодизации здоровья населения в России с помощью метода шаров. 20
3.2 Периодизации здоровья населения в России с помощью метода дендритов. 22
3.3 Периодизации здоровья населения в России с помощью метода корреляционных плеяд. 25
Заключение. 30
Список литературы. 32
Введение
Изучение динамики и состояния экономических и социальных процессов относится к числу существенных направлений на современном этапе развития любой страны мира.
Как известно эти явления описываются не одним показателем, а системой показателей. Среди многочисленных проблем, возникших при статистическом исследовании социально –экономической динамики, важное место занимает задача выделения однородных периодов развития - задача периодизации.
Периодизация может осуществляться разными методами. Одним из направлений этих методов являются эвристические методы.
Эвристические методы прогнозирования основаны на приемах вычисления и процедурах, вытекающих из опыта и интуиции специалистов, осуществляющих прогноз. И используются в тех случаях, когда применение строгих математических моделей не обеспечивает достоверных результатов прогноза из-за того, что лежащие в их основе предпосылки не соответствуют реальным свойствам поведения прогнозируемого процесса или объекта, что является актуальностью данной работы.
Реклама

Целью работы является изучение методологии эвристических методов, реализация их на практике по показателям здоровья России и анализ полученных данных , что достигается с помощью рассмотрения следующих вопросов:
1. Понятие периодизации и ее возможность;
2. Понятие однородности периодов;
3. Методология эвристических методов;
4. Достоинства и недостатки данных методов;
1. Понятие периодизации, необходимость и возможность.
1.1 Сущность и условия временной периодизации
.
Главное условие осуществления статистических расчетов – однородность данных. Иначе говоря, типология исходной информации представляет собой начальный, обязательный этап анализа.
Как правило, качественному скачку в динамике процесса, приводящему к смене закономерности, предшествует его непрерывное количественное изменение. Следовательно, при изучении хронологических рядов, охватывающих большие периоды времени, важно расчленять их на однородные интервалы. Однородность совокупности реализуется по средством типологической группировки. В хронологических рядах этим целям призвана служить периодизация
– разбиение динамических рядов на интервалы однокачественного развития. Периодизация важна и в историческом аспекте как процесс определения однородных периодов общественного развития.
По существу, периодизация является своеобразной типологической группировкой, в которой в качестве элементов совокупности, подлежащей разбиению, выступают уровни изолированного или комплексного хронологического ряда. Периодизация, с одной стороны, дает важную информацию о процессе, с другой- закладывает основы для последующего анализа динамики, так как обеспечивает возможность применения методов многомерной статистики; адекватное их использование возможно лишь в однородных сферах. Однако, в отличие от типологической группировки, периодизация исключительно редко используется в расчетах, соответственно и теория ее применения практически не разработана, нет устоявшихся корректных статистических методов ее реализации. Причин данной ситуации несколько, и основная заключается в противоречивости различных условий применения алгоритмов корреляционно-регрессионного анализа(КРА) в рядах динамики. Как известно, к числу основных условий применения КРА относятся:
1)наличие случайной выборки из генеральной совокупности;
2)достаточно большое число наблюдений;
3)независимость наблюдений;
4)значительное превышение численности единиц совокупности числа факторов( в 6-8 раз)
Реклама

5)однородность совокупности;
6)количественный уровень оценки переменных.
Нельзя не заметить противоречие между пунктом 5, с одной стороны, и пунктами 2 и 4 – с другой. Интервалы однокачественной динамики в реальности могут быть невелики по величине; в то же время значительные хронологические промежутки часто формируются разными законами развития. В анализе рядов динамики приоритет отдается количественным подходам к содержанию статистических исследований, что связано с выполнением условий 2 и 4 и соответственно с игнорированием условия 5.
Итак, особенность исследований динамики состоит в том, что одновременное выполнение приведенных выше условий вряд ли возможно. В этом случае обязательным является выполнение однородности, даже в ущерб прочим условиям.
В том случае, когда рассматривают уровни ряда, то получают периодизацию состояния. Если же абсолютные приросты или темпы поста или прироста выполняется периодизация динамики процесса. В случаи периодизации могут быть использованы следующие названия периодов: крупный, средний, мелкий(предприятие); низкое, среднее, высокое(здоровье), а если периодизацию динамики: подъем, стабильность, спад.
1.2 Однородность временных рядов.
Следует разобраться что же значит однородность временных рядов.
Однородными принято считать такие хронологические интервалы, в пределах которых изменение уровней ряда подчинено одному закону развития. Это определение, вполне корректно с теоретических позиций, мало что дает в практическом аспекте. Поэтому в дальнейшем однородным будем считать временной промежуток, соответствующий одной из следующих ситуаций, имеющих корректную интерпретацию:
1)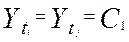 - равенство уровней ряда(здесь и далее равенство понимается в статистическом смысле); - равенство уровней ряда(здесь и далее равенство понимается в статистическом смысле);
2) - равенство абсолютных приростов(постоянная скорость изменения уровней ряда); - равенство абсолютных приростов(постоянная скорость изменения уровней ряда);
3) -равенство вторых абсолютных разностей(постоянно ускоренное или замедленное изменение уровней ряда); -равенство вторых абсолютных разностей(постоянно ускоренное или замедленное изменение уровней ряда);
4) 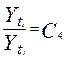 - равенство цепных темпов роста. - равенство цепных темпов роста.
Здесь  , , 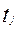 - отдельные моменты или промежутки времени; - отдельные моменты или промежутки времени;
 - цепные абсолютный прирост; - цепные абсолютный прирост;
 - вторая разность уровней ряда динамики. - вторая разность уровней ряда динамики.
Традиционно наметка однокачественных периодов осуществляется в соответствии с теоретическим анализом применительно к той науке, в рамках которой рассматривается изучаемый процесс. При этом стараются учитывать прежде всего крупные аномалии(войны, эпидемии, землетрясения),смену руководства страны и пр.
2. Эвристические методы периодизации.
2.1 Предварительные процедуры.
Прежде чем прибегнуть к помощи методов сравнительного анализа, необходимо выполнить определенные преобразования. Исходным и одновременно самым важным шагом, предопределяющим правильность конечных результатов, является формирование матрицы наблюдений
. Эта матрица содержит наиболее полную характеристику изучаемого множества и благодаря этому играет важнейшую роль в проводимом исследовании. В качестве элементов данной матрицы мы можем рассматривать уровни ряда, абсолютные приросты, темпы роста или темпы прироста.
 Допустим, у нас имеется множество из m элементов, описываемых k признаками; тогда каждую единицу можно интерпретировать как точку n-мерного пространства с координатами, равными значениям k признаков для рассматриваемой единицы. Вышеуказанную матрицу наблюдений можно представить следующим образом: Допустим, у нас имеется множество из m элементов, описываемых k признаками; тогда каждую единицу можно интерпретировать как точку n-мерного пространства с координатами, равными значениям k признаков для рассматриваемой единицы. Вышеуказанную матрицу наблюдений можно представить следующим образом:
Где m- число единиц, n-число признаков,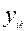 - значение признака kдля единицы i. - значение признака kдля единицы i.
Признаки, включенные в матрицу наблюдений, неоднородны, поскольку описывают разные свойства объектов. Кроме того, различаются их единицы измерения, что еще более затрудняет выполнение некоторых арифметических действий, необходимых в отдельных процедурах. Поэтому необходимо привести данные в сопоставимый вид
, это можно сделать либо с помощью стандартизации или с помощью нормирования.
Стандартизация производится в соответствии с формулой
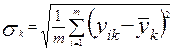 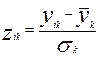 , причем , причем 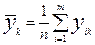 ; ;
Где k = 1,2,…,n ; 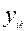 - значение признака k для единицы i; - значение признака k для единицы i;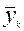 - среднее арифметическое значение признака k; - среднее арифметическое значение признака k;  - стандартное отклонение признака k; - стандартное отклонение признака k;  - стандартизованное значение. - стандартизованное значение.
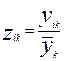 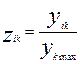 Нормирование проводится в соответствии с формулами: Нормирование проводится в соответствии с формулами:
или
После приведения данных в сопоставимый вид переходят к заключительной процедуре – расчету элементов матрицы сходства
. Сходство может рассматриваться в 2-х аспектах.
1)сходными считаются годы(моменты времени), между которыми незначимые расстояния, и соответственно в качестве матрицы сходства берется матрица расстояний: чем меньше расстояние между годами тем они имеют больше сходство по данной системе показателей. В настоящее время существует более 10 алгоритмов расчета расстояний между объектами, но чаще используются 2 алгоритма:
Среднее абсолютное расстояние 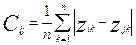 (i,j=1,2,…,m) (i,j=1,2,…,m)
Среднее Эвклидово расстояние 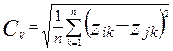
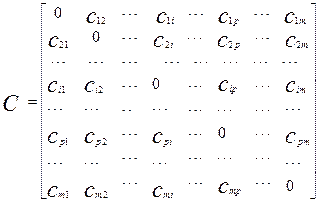 После исчисления расстояния между всеми единицами данной совокупности получаем матрицу расстояний. Ее можно представить в следующем виде: После исчисления расстояния между всеми единицами данной совокупности получаем матрицу расстояний. Ее можно представить в следующем виде:
Где символ  обозначает расстояние между элементами i и j. обозначает расстояние между элементами i и j.
Элементы этой матрицы служат основой для проведения исследований с помощью таксономических процедур. Они обладают следующими свойствами:
1. 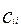 =0 =0
2.  = =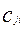
3. неравенство треугольника  <= <=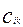 + +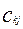
Те методы классификации, в которых используется в качестве матрицы сходства матрица расстояний, называются таксономическими.
2)В качестве матрицы сходства может быть использована матрица коэффициентов корреляции.
Эту матрицу можно представить следующим образом:
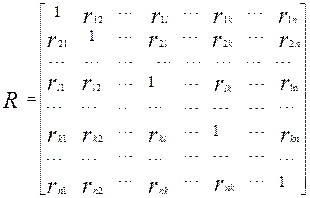
Где символ 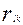 обозначает линейный коэффициент корреляции признаков l и k. обозначает линейный коэффициент корреляции признаков l и k.
Свойства матрицы корреляции:
1. 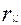 =1 =1
2. 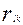 = =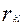
3. 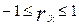
Методы классификации основанные на матрицах корреляции называются факторными.
В данном случае чем выше взаимосвязь между моментами времени по изучаемой системе показателей тем выше их сходство.
2.1 Вроцлавская таксономия: дендрит.
Метод вроцлавской таксономии часто называют методом дендритов. Под дендритом понимают ломаную, которая может разветвляться, но не может содержать замкнутых линий, и такая, что любые две точки множества Z ею соединены.Этим методом получают нелинейное упорядочение изучаемых единиц, что, с одной стороны, полнее характеризует действительность, но, с другой стороны, создает больше трудностей при интерпретации. Нелинейное упорядочение характеризуется отсутствием явной иерархии, выражающимся в том, что некоторые единицы могут быть связаны с большим числом других единиц. В этом случае отсутствует четко определяемый порядок, не известно, какой элемент является предшествующим, а какой последующим.
 Рассматриваемые случаи упорядочения можно представить графически в виде точек или кружков(со вписанными в них обозначаемыми единиц), связанных отрезками. Точки, изображающие единицы, чаще всего называются вершинами, а отрезки – связями(дугами). Упомянутые линейный и нелинейный способы упорядочения иллюстрируют рис.1 и рис.2. Рассматриваемые случаи упорядочения можно представить графически в виде точек или кружков(со вписанными в них обозначаемыми единиц), связанных отрезками. Точки, изображающие единицы, чаще всего называются вершинами, а отрезки – связями(дугами). Упомянутые линейный и нелинейный способы упорядочения иллюстрируют рис.1 и рис.2.

Рис.2.1 Линейное упорядочение единиц
Рис.2.2 Нелинейные упорядочения единиц
Предоставленные на рисунках упорядочения, очевидно, не исчерпывают все возможные ситуации. В связи с этим возникает задача выбора наилучшего упорядочения, заключающегося в нахождении такого дендрита, в котором смежные единицы будут иметь различающиеся значения признаков. Выполнение этого условия приведет к упорядочению с наименьшими расстояниями между отдельными элементами. В оптимальном дендрите – с наименьшей суммой длин связей – смежные объекты в наименьшей степени отличаются друг от друга. Поэтому при сравнении различных упорядочений объектов и выборе наилучшего упорядочения исходят из длины связей дендрита.
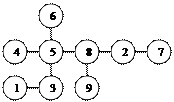
Построение оптимального дендрита заключается в установлении связей между единицами, наименее отличающимися друг от друга. С этой целью из составленной матрицы расстояний выбирают единицы с близкими значениями признаков. Поиск таких единиц проводится путем нахождения наименьших чисел в каждом столбце (или строке) матрицы. Искомые ближайшие единицы обозначены номерами строк(или столбцов), в которых находятся наименьшие числа. Если, например, надо найти единицу, наименее отличающуюся от i, то достаточно отыскать наименьшее число в столбце j. Пусть этим числом будет элемент 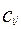 , находящийся в строке i. Тогда ближайшей к единице iбудет единица j. , находящийся в строке i. Тогда ближайшей к единице iбудет единица j.
Способ построения оптимального дендрита состоит из нескольких этапов. На первом этапе устанавливаются связи каждой из исследуемых единиц с ближайшими единицами.
Для удобства описания выполняемых операций предположим, что у нас имеется множество единиц, обозначаемых символами 1,2,3,4,5,6,7,8,9. Далее предположим, что в этом множестве из девяти элементов получены следующие сочетания ближайших единиц(рис.3).

Рис.2.3 Сочетание ближайших единиц
Нетрудно заметить, что некоторые связи встречаются дважды, например 1-3 и 3-1. Поскольку при построении дендрита очередность установления связей не играет роли, одно из повторяющихся сочетаний всегда исключаются. Подобное исключение проводится для всех выделенных пар связей. Это приводит к тому, что остаются связи 2-7 и 8-9, а связи 7-2 и 9-8 отбрасываются. Для оставшихся двух связей характерно наличие единицы, обозначаемой номером 5, поэтому связи 4-5 и 5-6 объединяют в один общий набор. В результате получаются четыре отдельных конструкций, называемые скоплениями 1-го порядка(рис.4).
Рис.2.4 Скопления 1-го порядка.
 Полученные скопления не удовлетворяют основному условию дендрита, а именно они не связаны в единое целое. Для выполнения этого требования выбирается наименьшее расстояние между единицами, входящими в различные скопления 1-го порядка. Соответствующий отрезок становится связью между двумя скоплениями. В результате получают скопление 2-го порядка. Процесс останавливаем на том шаге, когда все точки множества будут соединены ломаной(рис.5). Полученные скопления не удовлетворяют основному условию дендрита, а именно они не связаны в единое целое. Для выполнения этого требования выбирается наименьшее расстояние между единицами, входящими в различные скопления 1-го порядка. Соответствующий отрезок становится связью между двумя скоплениями. В результате получают скопление 2-го порядка. Процесс останавливаем на том шаге, когда все точки множества будут соединены ломаной(рис.5).
Рис.2.5 Дендрит, построенный на единицах исследуемого множества
Разбиение оптимального дендрита на группы однородных элементов может осуществляться одним из 2-х способов:
1)Искусственное разбиение. Пусть на основании некоторой априорной информации нам известно число однородных грум и пусть это число равно k. Тогда разбиение осуществляется очень просто: из дендрита удаляются k-1самых длинных связей.
2)Естественное разбиение. Что произвести подобное естественное разбиение, необходимо выполнить следующие действия. Прежде всего, связи дендрита, построенного на единицах изучаемого множества, упорядочиваются по убыванию их длины. Затем строятся отношения длин соседних связей:
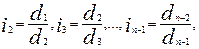 , ,
Где 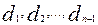 - упорядоченные длины связей, - упорядоченные длины связей, 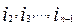 - отношения длин связей. - отношения длин связей.
Следующая операция заключается в нахождении значения k, для которого выполняется соотношение, являющееся основанием разбиения множества естественным образом. Этой цели служит неравенство:
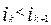 (для k=2,3,…,n-1) (для k=2,3,…,n-1)
Может оказаться, что в ряду вычисленных отношений приведенное неравенство будет выполнятся несколько раз. В этом случае вводится дополнительное условие. Оно позволяет выбрать лучшее из двух естественных разбиений 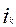 и и 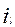 . Это дополнительное условие определяется соотношением . Это дополнительное условие определяется соотношением 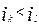 . Если оно выполняется, то можно утверждать, что лучшим является разбиение на k частей. . Если оно выполняется, то можно утверждать, что лучшим является разбиение на k частей.
2.2 Метод шаров.
Перед описанием этого метода дадим геометрическую модель для простейшего случая двумерного пространства. Единицы исследуемого множества характеризуются только двумя признаками и изображаются точками на плоскости. Тогда их можно представить как множество точек 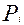 с координатами ( с координатами (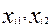 ) при i=1,…,w, причем w- число элементов множества. ) при i=1,…,w, причем w- число элементов множества.
Для выполнения дальнейших преобразований необходимо знать некоторую величину 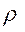 . Если эта величина известна, то поступают следующим образом. Из каждой точки . Если эта величина известна, то поступают следующим образом. Из каждой точки 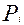 , как центра, строится круг радиусом , как центра, строится круг радиусом 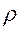 . Затем подсчитывается число точек, находящихся внутри каждого круга. Тем самым находится первое подмножество. Элементами его являются элементы круга, содержащего наибольшее число точек. Если есть несколько кругов с одним и тем же числом точек, то первое подмножество образуют точки круга, центр которого расположен ближе всего к началу системы координат. . Затем подсчитывается число точек, находящихся внутри каждого круга. Тем самым находится первое подмножество. Элементами его являются элементы круга, содержащего наибольшее число точек. Если есть несколько кругов с одним и тем же числом точек, то первое подмножество образуют точки круга, центр которого расположен ближе всего к началу системы координат.
Дальнейшее разбиение производится подобным же образом, но число элементов множества уменьшается за счет элементов первого подмножества
Рис.2.6 Разбиение множества единиц, характеризуемых двумя признаками.
На рис. 2.6 показано расположение пяти точек-единиц. Поскольку эти единицы описываются только двумя признаками, их можно поместить на плоскости. После вычерчивания кругов и подсчета числа точек в них не трудно убедится, что первое подмножество образуют точки- единицы заштрихованного круга.
Опишем теперь общий порядок действий, относящихся к пространству произвольной размерности.
Пусть дано множество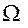 точек точек 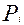 с координатами ( с координатами (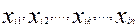 ), причем i=1,2,…,w. Для каждой точки ), причем i=1,2,…,w. Для каждой точки 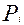 строится шар заданного радиуса строится шар заданного радиуса 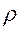 : :
 . .
Затем подсчитывается число точек 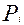 ,находящихся внутри каждого шара: ,находящихся внутри каждого шара:  , где , где 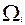 обозначает подмножество i множества обозначает подмножество i множества 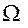 . Оно образовано точками . Оно образовано точками  , удовлетворяющими условию , удовлетворяющими условию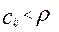 . .
Если обозначить через 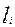 , объем подмножества , объем подмножества 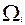 , то , то 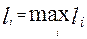 - величина, определяющая первое выделяемое подмножество. В случае существования нескольких подмножеств с максимальным объемом исчисляют расстояния центров выбранных шаров от начала системы координат. Первое подмножество образуют единицы, содержащиеся в шаре, ближе всего находящегося от начала системы координат. Это подмножество обозначаем символом - величина, определяющая первое выделяемое подмножество. В случае существования нескольких подмножеств с максимальным объемом исчисляют расстояния центров выбранных шаров от начала системы координат. Первое подмножество образуют единицы, содержащиеся в шаре, ближе всего находящегося от начала системы координат. Это подмножество обозначаем символом 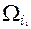 . .
Дальнейшие действия производятся таким же самым образом , только относятся не ко всем объектам, а лишь к тем, которые остались после исключения первого подмножества. Это значит, что при дальнейшем выделении подмножеств рассматривается множество 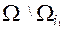 . .
Описанная процедура, очевидно, продолжается до момента полного исчерпания множества 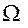 . .
Теперь осталось выяснить проблему, связанную с оценкой величины 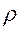 . При оценке этой величины рассматривают два случая: . При оценке этой величины рассматривают два случая:
В первом 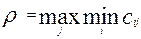
Во втором  , причем , причем 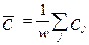 ; ;  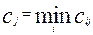 , где i,j=1,2,…,w. , где i,j=1,2,…,w.
Величина 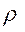 остается постоянной. остается постоянной.
В результате применения рассмотренного метода получаются подмножества, однородные в смысле изотропности, т.е. подмножества точек-данных, которые расположены в многомерном пространстве так, что по форме облако рассеивания больше похоже на шар чем на эллипсоид.
С точки зрения потребностей экономического моделирования подобные подмножества представляют собой результат искусственного , навязанного, а не естественного разбиения исследуемой совокупности объектов. При таком способе разбиения существует потенциальная возможность разделить действительно однородные объекты. Подобное нежелательное разбиение может возникнуть вследствие того, что в значениях признаков присутствуют обе компоненты( структуры и потенциала).
2.3 Метод корреляционных плеяд.
Метод корреляционных плеяд самый первый из эвристических методов классификации данных и он наименее формализован. Выглядит этот метод очень трудоемким особенно это становится явным при достаточно большом числе объектов.
Преимущество этого метода в том что он учитывает все связи он не отбрасывает как два предыдущих метода «не нужную информацию». Исторически метод корреляционных плеяд применяется и используется до сих пор к матрицам корреляции. Но в принципе технику этого метода можно применить и получить корректные данные на матрицах расстояний.
Осуществляется следующим образом:
В матрице коэффициентов корреляции выбирается максимальный по абсолютной величине коэффициент корреляции( не считая диагональных). Пусть им оказался  . Чертим два кружка, соответствующие признакам . Чертим два кружка, соответствующие признакам  и и  , и соединяем их линией, над которой пишем значение , и соединяем их линией, над которой пишем значение 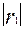 . Затем находим наибольший по абсолютной величине коэффициент в . Затем находим наибольший по абсолютной величине коэффициент в -том столбце матрицы корреляции( он будет соответствовать признаку, наиболее тесно после -том столбце матрицы корреляции( он будет соответствовать признаку, наиболее тесно после 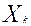 связанному с связанному с  ). Выбираем больший из этих двух коэффициентов. Пусть им оказался ). Выбираем больший из этих двух коэффициентов. Пусть им оказался 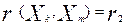 . Чертим кружок . Чертим кружок  , соединяем его с кружком , соединяем его с кружком 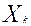 , над связью пишем , над связью пишем 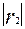 . Далее находим признаки, наиболее тесно связанные с двумя последними рассмотренными( в данном случае . Далее находим признаки, наиболее тесно связанные с двумя последними рассмотренными( в данном случае 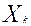 и и  ), и повторяя процедуру выбора, выбираем из двух соответствующих коэффициентов корреляции наибольший по абсолютной величине. Продолжая построение, на каждом шаге находим признак, наиболее тесно связанный с одним из двух признаков, отобранных на предыдущем этапе. Построение чертежа завершим, когда в нем окажется m кружков(m - число признаков). Выбираем пороговую величину h и исключаем из схемы связи, соответствующие меньшим чем h коэффициентам парной корреляции. Величину h выбираем до тех пор, пока не получим нормальных групп(плеяд) признаков(h является порогом, при переходе через который происходит рассеивание групп на отдельные, не связанные признаки). ), и повторяя процедуру выбора, выбираем из двух соответствующих коэффициентов корреляции наибольший по абсолютной величине. Продолжая построение, на каждом шаге находим признак, наиболее тесно связанный с одним из двух признаков, отобранных на предыдущем этапе. Построение чертежа завершим, когда в нем окажется m кружков(m - число признаков). Выбираем пороговую величину h и исключаем из схемы связи, соответствующие меньшим чем h коэффициентам парной корреляции. Величину h выбираем до тех пор, пока не получим нормальных групп(плеяд) признаков(h является порогом, при переходе через который происходит рассеивание групп на отдельные, не связанные признаки).
Может быть предложен более формальный подход к реализации метода корреляционных плеяд, заключающийся в следующем. В завершенном чертеже m кружков соединяют от (m-1) до (m(m-1):2) связей. Очевидно, что исключение не каждой связи приводит к появлению новой неодноэлементной группы(плеяды) признаков, поэтому оставим на чертеже только существенные связи, т.е. те, исключая которые мы обязательно увеличиваем число плеяд. Их будет m-1. В результате получим тот же дендрит. Для выделения корреляционных групп теперь можно применить те же критерии, что и в методе дендритов.
3. Периодизация здоровья в Российской Федерации за 1991- 2005 гг.
3.1 Предварительные процедуры
.
В качестве параметров здоровья в стране взяты: смертность, рождаемость, общая продолжительность жизни, продолжительность жизни мужчин, продолжительность жизни женщин, детская смертность, заболеваемость населения злокачественными новообразованиями, т.е исходная информация представлена виде комплексного ряда динамики(таблица 1).
Таблица 1
Показатели здоровья по РФ за 1991- 2005 гг
| Годы
|
Смертность (на тыс.)
|
Рождаемость (на тыс.)
|
Общая продолжительность жизни (лет)
|
Продолжительность жизни мужчин (лет)
|
Продолжительность жизни женщин (лет)
|
Детская смертность (на тыс. родившихся)
|
Заболеваемость населения злокачественными новообразованиями (на 100 тыс.)
|
| 1991
|
11,4
|
12,1
|
69,01
|
63,46
|
74,27
|
17,8
|
266
|
| 1992
|
12,2
|
10,7
|
67,89
|
62,02
|
73,75
|
18,0
|
272
|
| 1993
|
14,5
|
9,4
|
65,14
|
58,91
|
71,88
|
19,9
|
276
|
| 1994
|
15,7
|
9,6
|
63,98
|
57,59
|
71,18
|
18,6
|
280
|
| 1995
|
15,0
|
9,3
|
64,64
|
58,27
|
71,70
|
18,1
|
279
|
| 1996
|
14,2
|
8,9
|
65,89
|
59,75
|
72,49
|
17,4
|
288
|
| 1997
|
13,8
|
8,6
|
66,64
|
60,75
|
72,89
|
17,2
|
295
|
| 1998
|
13,6
|
8,8
|
67,02
|
61,30
|
72,93
|
16,5
|
302
|
| 1999
|
14,7
|
8,3
|
65,93
|
59,93
|
72,38
|
16,9
|
304
|
| 2000
|
15,4
|
8,7
|
65,27
|
59,00
|
72,20
|
15,3
|
307
|
| 2001
|
15,6
|
9,0
|
65,23
|
58,92
|
72,17
|
14,6
|
311
|
| 2002
|
16,2
|
9,7
|
64,95
|
58,68
|
71,90
|
13,3
|
314
|
| 2003
|
16,4
|
10,2
|
64,85
|
58,55
|
71,84
|
12,4
|
317
|
| 2004
|
16,0
|
10,4
|
65,27
|
58,89
|
72,30
|
11,6
|
328
|
| 2005
|
16,1
|
10,2
|
65,30
|
58,87
|
72,39
|
11,0
|
330
|
Затем переводим данные в сопоставимый вид, с помощью стандартизации данных. Для этого необходимо рассчитать вспомогательные показатели: среднее значение и среднее квадратическое отклонение. Рассчитанные показатели представлены в таблице 2
Таблица 2
Вспомогательные показатели для расчета
стандартизованных данных
| показатели
|
Смертность (на тыс.)
|
Рождаемость (на тыс.)
|
Общая продолжительность жизни (лет)
|
Продолжительность жизни мужчин (лет)
|
Продолжительность жизни женщин (лет)
|
Детская смертность (на тыс. родившихся)
|
Заболеваемость населения злокачественными новообразованиями (на 100 тыс.)
|
| среднее значение
|
14,720
|
9,593
|
65,801
|
59,659
|
72,418
|
15,907
|
297,933
|
| среднее квадратическое отклонение
|
1,429
|
0,964
|
1,284
|
1,531
|
0,764
|
2,646
|
19,699
|
А стандартизованные данные примут следующий вид (таблица 3)
Таблица 3
Стандартизованные показатели здоровья
| Годы
|
Смертность (на тыс.)
|
Рождаемость (на тыс.)
|
Общая продолжительность жизни (лет)
|
Продолжительность жизни мужчин (лет)
|
Продолжительность жизни женщин (лет)
|
Детская смертность (на тыс. родившихся)
|
Заболеваемость населения злокачественными новообразованиями (на 100 тыс.)
|
| 1991
|
-2,3236
|
2,5994
|
2,4986
|
2,4831
|
2,4235
|
0,7156
|
-1,6210
|
| 1992
|
-1,7637
|
1,1476
|
1,6267
|
1,5423
|
1,7431
|
0,7912
|
-1,3165
|
| 1993
|
-0,1540
|
-0,2005
|
-0,5144
|
-0,4896
|
-0,7040
|
1,5093
|
-1,1134
|
| 1994
|
0,6859
|
0,0069
|
-1,4175
|
-1,3520
|
-1,6200
|
1,0179
|
-0,9104
|
| 1995
|
0,1960
|
-0,3042
|
-0,9036
|
-0,9077
|
-0,9396
|
0,8290
|
-0,9611
|
| 1996
|
-0,3639
|
-0,7190
|
0,0696
|
0,0592
|
0,0942
|
0,5644
|
-0,5042
|
| 1997
|
-0,6439
|
-1,0301
|
0,6535
|
0,7126
|
0,6177
|
0,4888
|
-0,1489
|
| 1998
|
-0,7838
|
-0,8227
|
0,9493
|
1,0719
|
0,6700
|
0,2242
|
0,2064
|
| 1999
|
-0,0140
|
-1,3412
|
0,1007
|
0,1768
|
-0,0497
|
0,3754
|
0,3080
|
| 2000
|
0,4759
|
-0,9264
|
-0,4132
|
-0,4308
|
-0,2853
|
-0,2293
|
0,4603
|
| 2001
|
0,6159
|
-0,6153
|
-0,4443
|
-0,4830
|
-0,3245
|
-0,4939
|
0,6633
|
| 2002
|
1,0358
|
0,1106
|
-0,6623
|
-0,6398
|
-0,6779
|
-0,9852
|
0,8156
|
| 2003
|
1,1758
|
0,6291
|
-0,7401
|
-0,7248
|
-0,7564
|
-1,3253
|
0,9679
|
| 2004
|
0,8958
|
0,8365
|
-0,4132
|
-0,5026
|
-0,1544
|
-1,6277
|
1,5263
|
| 2005
|
0,9658
|
0,6291
|
-0,3898
|
-0,5157
|
-0,0366
|
-1,8545
|
1,6278
|
А уже по стандартизованным данным рассчитываем матрицу расстояний по среднему Эвклидову расстоянию[1]
. Результаты представлены в таблице 4.
Матрица расстояний Таблица 4
| 1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
| 1
|
0
|
0,813
|
2,424
|
2,994
|
2,662
|
2,182
|
2,000
|
1,895
|
2,446
|
2,667
|
2,690
|
2,820
|
2,876
|
2,749
|
2,809
|
| 2
|
0,813
|
0
|
1,676
|
2,283
|
1,915
|
1,389
|
1,216
|
1,154
|
1,668
|
1,915
|
1,964
|
2,154
|
2,255
|
2,173
|
2,231
|
| 3
|
2,424
|
1,676
|
0
|
0,700
|
0,378
|
0,639
|
1,032
|
1,233
|
0,916
|
0,972
|
1,075
|
1,282
|
1,461
|
1,660
|
1,742
|
| 4
|
2,994
|
2,283
|
0,700
|
0
|
0,431
|
1,143
|
1,570
|
1,750
|
1,271
|
1,068
|
1,104
|
1,140
|
1,267
|
1,583
|
1,666
|
| 5
|
2,662
|
1,915
|
0,378
|
0,431
|
0
|
0,729
|
1,164
|
1,358
|
0,919
|
0,802
|
0,881
|
1,037
|
1,212
|
1,466
|
1,540
|
| 6
|
2,182
|
1,389
|
0,639
|
1,143
|
0,729
|
0
|
0,439
|
0,648
|
0,421
|
0,646
|
0,773
|
1,096
|
1,305
|
1,391
|
1,441
|
| 7
|
2,000
|
1,216
|
1,032
|
1,570
|
1,164
|
0,439
|
0
|
0,261
|
0,500
|
0,879
|
0,993
|
1,334
|
1,535
|
1,528
|
1,559
|
| 8
|
1,895
|
1,154
|
1,233
|
1,750
|
1,358
|
0,648
|
0,261
|
0
|
0,647
|
0,992
|
1,074
|
1,382
|
1,560
|
1,501
|
1,527
|
| 9
|
2,446
|
1,668
|
0,916
|
1,271
|
0,919
|
0,421
|
0,500
|
0,647
|
0
|
0,461
|
0,611
|
0,997
|
1,233
|
1,299
|
1,324
|
| 10
|
2,667
|
1,915
|
0,972
|
1,068
|
0,802
|
0,646
|
0,879
|
0,992
|
0,461
|
0
|
0,182
|
0,579
|
0,827
|
0,956
|
0,981
|
| 11
|
2,690
|
1,964
|
1,075
|
1,104
|
0,881
|
0,773
|
0,993
|
1,074
|
0,611
|
0,182
|
0
|
0,408
|
0,652
|
0,779
|
0,805
|
| 12
|
2,820
|
2,154
|
1,282
|
1,140
|
1,037
|
1,096
|
1,334
|
1,382
|
0,997
|
0,579
|
0,408
|
0
|
0,253
|
0,510
|
0,559
|
| 13
|
2,876
|
2,255
|
1,461
|
1,267
|
1,212
|
1,305
|
1,535
|
1,560
|
1,233
|
0,827
|
0,652
|
0,253
|
0
|
0,386
|
0,454
|
| 14
|
2,749
|
2,173
|
1,660
|
1,583
|
1,466
|
1,391
|
1,528
|
1,501
|
1,299
|
0,956
|
0,779
|
0,510
|
0,386
|
0
|
0,133
|
| 15
|
2,809
|
2,231
|
1,742
|
1,666
|
1,540
|
1,441
|
1,559
|
1,527
|
1,324
|
0,981
|
0,805
|
0,559
|
0,454
|
0,133
|
0
|
Выполнены все предварительные процедуры и можно применить эвристические методы периодизации.
3.2 Периодизации здоровья населения в России с помощью метода шаров.
В матрице расстояний(таблица 4) в каждом столбце определяем минимальное расстояние и из этих расстояний выбираем самое максимальное – это будет радиус шара(величина постоянная), а потом под считываем количество точек для каждого круга. В эти круги не включаются элементы находящиеся на «внешней» стороне круга. Результаты представлены в таблице 5. Таблица 5
Определение радиуса шара и первого подмножества
| 1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
13
|
14
|
15
|
радиус шара
|
| минимальное по столбцу
|
0,813
|
0,813
|
0,378
|
0,431
|
0,378
|
0,421
|
0,261
|
0,261
|
0,421
|
0,182
|
0,182
|
0,253
|
0,133
|
0,133
|
0,813
|
| число точек в шаре
|
1
|
1
|
4
|
3
|
5
|
8
|
4
|
4
|
6
|
6
|
8
|
5
|
5
|
5
|
Из таблицы видно, что в качестве первого подмножества могут выступать либо шар 6 либо шар 11. В качестве первого подмножества берется тот шар, который находится ближе к началу координат. Близость эта оценивается также по Эвклидовой метрике : рассчитывают 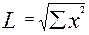 для каждого шара и чье расстояние меньше , тот и берется в качестве первого подмножества. для каждого шара и чье расстояние меньше , тот и берется в качестве первого подмножества.
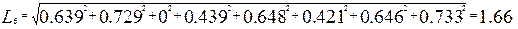
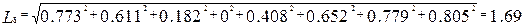
Значит в качестве первого подмножества будет выступать шар 6 (1,66<1.69).Этот шар содержит в себе следующие элементы: 3,5,6,7,8,9,10,11.
Дальнейшее разбиение проводится следующим образом только из матрицы расстояний удаляются строчки и столбцы принадлежащие элементам шара 6. (таблица 6) Таблица 6
| 1
|
2
|
4
|
12
|
13
|
14
|
15
|
| 1
|
0
|
0,813
|
2,994
|
2,820
|
2,876
|
2,749
|
2,809
|
| 2
|
0,813
|
0
|
2,283
|
2,154
|
2,255
|
2,173
|
2,231
|
| 4
|
2,994
|
2,283
|
0
|
1,140
|
1,267
|
1,583
|
1,666
|
| 12
|
2,820
|
2,154
|
1,140
|
0
|
0,253
|
0,510
|
0,559
|
| 13
|
2,876
|
2,255
|
1,267
|
0,253
|
0
|
0,386
|
0,454
|
| 14
|
2,749
|
2,173
|
1,583
|
0,510
|
0,386
|
0
|
0,133
|
| 15
|
2,809
|
2,231
|
1,666
|
0,559
|
0,454
|
0,133
|
0
|
| кол-во точек в шаре
|
1
|
1
|
1
|
4
|
4
|
4
|
4
|
Видно что в качестве второго подмножества может быть выбран либо шар12, либо шар13,либо шар14 ,либо шар 15. Рассчитываем также расстояния:
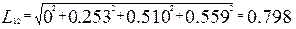
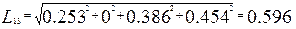
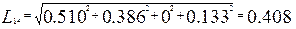
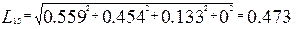
Значит в качестве второго подмножества будет выступать шар14, который содержит в себе следующие элементы: 12,13,14,15.
| 1
|
2
|
4
|
| 1
|
0
|
0,813
|
2,994
|
| 2
|
0,813
|
0
|
2,283
|
| 4
|
2,994
|
2,283
|
0
|
| кол-во точек в шаре
|
1
|
1
|
1
|
Удалив соответствующие строчки и столбцы получаем матрицу расстояний: Таблица 7
Из таблицы 7 в каждом из оставшихся шаров находится только один элемент. И мы получили три последующих подмножества например: третье подмножество это шар1, четверное подмножество это шар 2, и пятое подмножество это шар 4 .
Тогда получаем следующие периоды развития здоровья в России:
I
период 1993,1995-2001
– низкий уровень здоровья
II
период 2002 – 2005
- очень низкий уровень здоровья
Остальные годы являются переходными или аномальными, а именно: 1991,1992 и 1994.
3.2 Периодизации здоровья населения в России с помощью метода дендритов.
Из матрицы расстояний (таблица 4) выбираем элементы с близкими расстояниями. Результат представлен на рис 3.1.
Рис.3,1 Сочетание ближайших единиц
Как видно на рисунке 3,1 некоторые связи встречаются дважды, например 1-2 и 2-1. Поскольку при построении дендрита очередность установления связей не играет роли, одно из повторяющихся сочетаний всегда исключаются. Подобное исключение проводится для всех выделенных пар связей. Это приводит к тому, что остаются связи 1-2 ,3-5, 6-9, 7-8, 10-11, 12-13, 14-15 а связи 2-1, 5-3, 9-6, 8-7, 11-10, 13-12, 15-14 отбрасываются, а 3, 5 ,4 объединяем в один так как 5 является связующим звеном между 3 и 4. В результате получаем 7 отдельных конструкций - скопление первого порядка(рис 3,2).
Рис.3,2 Скопление первого порядка
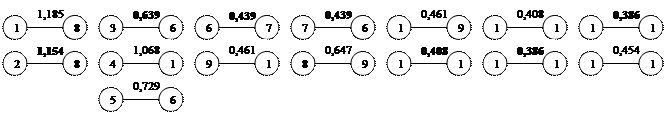 Затем находим связи более высокого порядка. Результаты представлены на рис 3,3. Затем находим связи более высокого порядка. Результаты представлены на рис 3,3.
Рис.3,3 сочетания ближайших единиц первого порядка
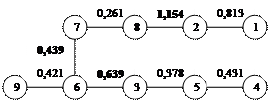 Дендрит второго порядка получается соединением 2 и 8, 3 и 6, 6 и 7, 11 и 12, 13 и 14. Результат представлен на рис 3,4. Дендрит второго порядка получается соединением 2 и 8, 3 и 6, 6 и 7, 11 и 12, 13 и 14. Результат представлен на рис 3,4.
Рис.3,4 Скопление второго порядка
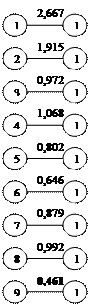  Находим связи еще более высокого порядка. Результаты представлены на рисунке 3,5. Находим связи еще более высокого порядка. Результаты представлены на рисунке 3,5.
Рис.3,5 Сочетание ближайших единиц скопления второго порядка.
Дендрит третьего порядка или оптимальный дендрит получается соединением 9 и 10 элемента(рис 3,6).
Рис.3,6 Оптимальный дендрит
Произведем разбиение дендрита естественным способом. Для этого упорядочим все связи по убыванию и найдем отношение соседних связей, и определяем нарушения закономерностей(закономерность –последующее отношение больше предыдущего). Результат представлен в таблице 8
Таблица 8
Вспомогательная таблица для определения количества периодов
| k
|
начало дуги
|
конец дуги
|
длина дуги
|
отношение связей
|
| 1
|
2
|
8
|
1,154
|
-
|
| 2
|
1
|
2
|
0,813
|
1,4186
|
| 3
|
3
|
6
|
0,639
|
1,2730
|
| 4
|
9
|
10
|
0,461
|
1,3847
|
| 5
|
6
|
7
|
0,439
|
1,0509
|
| 6
|
4
|
5
|
0,431
|
1,0188
|
| 7
|
6
|
9
|
0,421
|
1,0235
|
| 8
|
11
|
12
|
0,408
|
1,0320
|
| 9
|
13
|
14
|
0,386
|
1,0567
|
| 10
|
3
|
5
|
0,378
|
1,0208
|
| 11
|
7
|
8
|
0,261
|
1,4468
|
| 12
|
12
|
13
|
0,253
|
1,0347
|
| 13
|
10
|
11
|
0,182
|
1,3852
|
| 14
|
14
|
15
|
0,133
|
1,3690
|
Минимальным нарушением закономерности является 1,0188 и ему соответствует к=6, что означает разбиение оптимального дендрита на 6 групп, удалением при этом к-1 самых длинных связей. Результат разбиения представлен на рис.3,7.
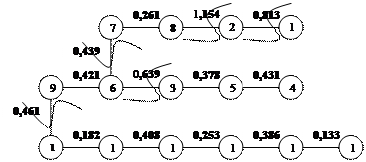
Рис.3,7 Разбиение оптимального дендрита
Как мы уже определили с помощью метода шаров состояние здоровья в России достаточно низкое. Тогда называть периоды будем относительно среднего уровня:
I
период 1997,1998 –
выше среднего уровень здоровья
II
период 1993-1995 -
средний уровень здоровья
III
период 1996,1999–
ниже среднего уровень здоровья
IV
период 2000-2005 –
критический или низкий уровень здоровья
Но при интерпретации состояния будем учитывать общую ситуацию , а также уровень относительно среднего.
Замечание
: периодизация с помощью метода дендритов выделила другие периоды развития ,чем периодизация с помощью метода шаров, но 1991 и 1992 также остались аномальными годами.
3.3 Периодизации здоровья населения в России с помощью метода корреляционных плеяд.
Как уже рассматривалось в теории метод корреляционных плеяд можно построить как по матрице коэффициентов корреляции ,так и по матрице расстояния. В данном случае этот метод будет выполнятся по матрице расстояний.
В матрице расстояний выбирается минимальное по абсолютной величине расстояние(за исключением диагонального).Минимальное расстояние оказалось между 14 и 15 (0,133). Соединяем эти два элемента - это соответствует шагу 1. Рассматриваем 14 столбец и выбираем в этом столбце минимальное значение кроме 0,133 (14-13(0,386))и рассматриваем 15-й столбец (15-13(0,454)). Из двух этих значений выбираем минимальное(т.е 0,386 и соединяем 13 и 14 ) это соответствует шагу 2. Процесс продолжается до полного исчерпания объектов множества. В данном случае до полного исчерпания 15 объектов. Весь алгоритм представлен в таблице 9.
Таблица 9
| шаг
|
рассматриваемые столбцы
|
уже выбранные значения
|
минимальное значение кроме выбранных
|
соединяем элементы
|
| 21
|
5
|
0,378 ;0,431; 0,919 ; 0,729
|
5-10(0,802)
|
6 и 10
|
| 6
|
0,648 ;0,639 ;0,729
|
6-10(0,646)
|
| 22
|
6
|
0,421; 0,439;0,648 ; 0,639;0,729 ; 0,646
|
6-11(0,773)
|
10 и 12
|
| 10
|
0,182; 0,461 ;0,646
|
10-12(0,579)
|
| 23
|
10
|
0,182; 0,461 ;0,646 ; 0,579
|
10-5(0,802)
|
12 и 14
|
| 12
|
0,253 ;0,408 ;0,579
|
12-14(0,510)
|
| 24
|
12
|
0,253 ;0,408 ;0,579; 0,510
|
12-15(0,559)
|
12 и 15
|
| 14
|
0,133 ;0,386; 0,510
|
14-11(0,779)
|
| 25
|
12
|
0,253 ;0,408 ;0,579; 0,510; 0,559
|
12-9(0,997)
|
15 и 13
|
| 15
|
0,133; 0,559
|
15-13(0,454)
|
| 26
|
15
|
0,133; 0,559; 0,454
|
15-11(0,805)
|
13 и 11
|
| 13
|
0,386 ;0,253; 0,454
|
13-11(0,652)
|
| 27
|
13
|
0,386 ;0,253; 0,454; 0,652
|
13-10(0,827)
|
11 и 6
|
| 11
|
0,408 ;0,182;0,611; 0,652
|
11-6(0,773)
|
| 28
|
11
|
0,408 ;0,182;0,611; 0,652; 0,773
|
11-14(0,779)
|
11 и 14
|
| 6
|
0,648 ;0,639 ;0,729 ; 0,646; 0,773
|
6-12(1,096)
|
| 29
|
11
|
0,408 ;0,182;0,611; 0,652; 0,773;0,779
|
11-15(0,805)
|
11 и 15
|
| 14
|
0,133 ;0,386; 0,510; 0,779
|
14-10(0,956)
|
| 30
|
11
|
0,408 ;0,182;0,611; 0,652; 0,773;0,779; 0,805
|
11-5(0,881)
|
11 и 5
|
| 15
|
0,133; 0,559; 0,454; 0,805
|
15-10(0,981)
|
| 31
|
11
|
0,408 ;0,182;0,611; 0,652; 0,773;0,779; 0,805; 0,881
|
11-7(0,993)
|
5 и 10
|
| 5
|
0,378 ;0,431; 0,919 ; 0,729;0,881
|
5-10(0,802)
|
| 32
|
5
|
0,378 ;0,431; 0,919 ; 0,729;0,881;0,802
|
5-12(1,037)
|
10 и 13
|
| 10
|
0,182; 0,461 ;0,646 ; 0,579; 0,802
|
10-13(0,827)
|
| 33
|
10
|
0,182; 0,461 ;0,646 ; 0,579; 0,802; 0,827
|
10-7(0,879)
|
10 и 7
|
| 13
|
0,386 ;0,253; 0,454; 0,652;0,827
|
13-5(1,212)
|
| 34
|
10
|
0,182; 0,461 ;0,646 ; 0,579; 0,802; 0,827;0,879
|
10-14(0,956)
|
10 и 14
|
| 7
|
0,439 ;0,261 ;0,500;0,879
|
7-11(0,993)
|
| шаг
|
рассматриваемые столбцы
|
уже выбранные значения
|
минимальное значение кроме выбранных
|
соединяем элементы
|
| 1
|
14 и 15
|
-
|
0,133
|
14 и 15
|
| 2
|
14
|
0,133
|
14-13(0,386)
|
14 и 13
|
| 15
|
0,133
|
15-13(0,454)
|
| 3
|
14
|
0,133 ;0,386
|
14-12(0,510)
|
13 и 12
|
| 13
|
0,386
|
13-12(0,253)
|
| 4
|
13
|
0,386 ;0,253
|
13-15(0,454)
|
12 и 11
|
| 12
|
0,253
|
12-11(0,408)
|
| 5
|
12
|
0,253 ;0,408
|
12-14(0,510)
|
11 и 10
|
| 11
|
0,408
|
11-10(0,182)
|
| 6
|
11
|
0,408 ;0,182
|
11-9(0,611)
|
10 и 9
|
| 10
|
0,182
|
10-9(0,461)
|
| 7
|
10
|
0,182; 0,461
|
10-12(0,579)
|
9 и 6
|
| 9
|
0,461
|
9-6(0,421)
|
| 8
|
9
|
0,461; 0,421
|
9-7(0,500)
|
6 и 7
|
| 6
|
0,421
|
6-7(0,439)
|
| 9
|
6
|
0,421; 0,439
|
6-3(0,639)
|
7 и 8
|
| 7
|
0,439
|
7-8(0,261)
|
| 10
|
7
|
0,439; 0,261
|
7-9(0,500)
|
7 и 9
|
| 8
|
0,261
|
8-9(0,647)
|
| 11
|
7
|
0,439 ;0,261 ;0,500
|
7-10(0,879)
|
9 и 11
|
| 9
|
0,461; 0,421;0,500
|
9-11(0,611)
|
| 12
|
9
|
0,461; 0,421;0,500 ; 0,611
|
9-8(0,647)
|
9и 8
|
| 11
|
0,408 ;0,182;0,611
|
11-13(0,652)
|
| 13
|
9
|
0,461; 0,421;0,500 ; 0,611;0,647
|
9-3(0,916)
|
8 и 6
|
| 8
|
0,261;0,647
|
8-6(0,648)
|
| 14
|
8
|
0,261;0,647 ;0,648
|
8-10(0,992)
|
6 и 3
|
| 6
|
0,421; 0,439;0,648
|
6-3(0,639)
|
| 15
|
6
|
0,421; 0,439;0,648 ;0,639
|
6-10(0,646)
|
3 и 5
|
| 3
|
0,639
|
3-5(0,378)
|
| 16
|
3
|
0,639 ;0,378
|
3-4(0,700)
|
5 и 4
|
| 5
|
0,378
|
5-4(0,431)
|
| 17
|
5
|
0,378 ;0,431
|
5-6(0,729)
|
4 и 3
|
| 4
|
0,431
|
4-3(0,700)
|
| 18
|
4
|
0,431 ;0,700
|
4-10(1,068)
|
3 и 9
|
| 3
|
0,639 ;0,378;0,700
|
3-9(0,916)
|
| 19
|
3
|
0,639 ;0,378;0,700 ; 0,916
|
3-10(0,972)
|
9 и 5
|
| 9
|
0,461; 0,421;0,500 ; 0,611;0,647 ; 0,916
|
9-5(0,919)
|
| 20
|
9
|
0,461; 0,421;0,500 ; 0,611;0,647; 0,916; 0,919
|
9-12(0,997)
|
5 и 6
|
| 5
|
0,378 ;0,431; 0,919
|
5-6(0,729)
|
Вспомогательная таблица для построения древа .
| шаг
|
рассматриваемые столбцы
|
уже выбранные значения
|
минимальное значение кроме выбранных
|
соединяем элементы
|
| 41
|
11
|
0,408 ;0,182;0,611; 0,652; 0,773;0,779; 0,805; 0,881; 1,104; 0,993
|
11-8(1,074)
|
7 и 3
|
| 7
|
0,439 ;0,261 ;0,500; 0,879; 0,993
|
7-3(1,032)
|
| 42
|
7
|
0,439 ;0,261 ;0,500; 0,879; 0,993;1,032
|
7-5(1,164)
|
3 и 11
|
| 3
|
0,639 ;0,378;0,700 ; 0,916; 0,972; 1,032
|
3-11(1,075)
|
| 43
|
3
|
0,639 ;0,378;0,700 ; 0,916; 0,972; 1,032;1,075
|
3-8(1,233)
|
11 и 8
|
| 11
|
0,408 ;0,182;0,611; 0,652; 0,773;0,779; 0,805; 0,881; 1,104; 0,993; 1,075
|
11-8(1,074)
|
| 44
|
11
|
0,408 ;0,182;0,611; 0,652; 0,773;0,779; 0,805; 0,881; 1,104; 0,993; 1,075; 1,074
|
11-2(1,964)
|
8 и 2
|
| 8
|
0,261;0,647; 0,648; 0,992; 1,074
|
8-2(1,154)
|
| 45
|
8
|
0,261;0,647; 0,648; 0,992; 1,074; 1,154
|
8-3(1,233)
|
2 и 1
|
| 2
|
1,154
|
2-1(0,183)
|
| шаг
|
рассматриваемые столбцы
|
уже выбранные значения
|
минимальное значение кроме выбранных
|
соединяем элементы
|
| 35
|
10
|
0,182; 0,461 ;0,646; 0,579; 0,802; 0,827;0,879; 0,956
|
10-15(0,981)
|
10 и 14
|
| 14
|
0,133 ;0,386; 0,510; 0,779;0,956
|
14-9(1,299)
|
| 36
|
10
|
0,182; 0,461 ;0,646; 0,579; 0,802;0,827; 0,879; 0,956;0,981
|
10-3(0,972)
|
10 и 3
|
| 15
|
0,133; 0,559; 0,454; 0,805; 0,981
|
15-9(1,324)
|
| 37
|
10
|
0,182; 0,461 ;0,646; 0,579; 0,802;0,827; 0,879; 0,956;0,981; 0,972
|
10-8(0,992)
|
10 и 8
|
| 3
|
0,639 ;0,378;0,700 ; 0,916; 0,972
|
3-7(1,032)
|
| 38
|
10
|
0,182; 0,461 ;0,646; 0,579; 0,802;0,827; 0,879; 0,956;0,981; 0,972;0,992
|
10-4(1,068)
|
10 и 4
|
| 8
|
0,261;0,647; 0,648; 0,992
|
8-11(1,074)
|
| 39
|
10
|
0,182; 0,461 ;0,646; 0,579; 0,802;0,827; 0,879; 0,956;0,981; 0,972;0,992; 1,068
|
10-2(1,915)
|
4 и 11
|
| 4
|
0,431 ;0,700;1,068
|
4-11(1,104)
|
| 40
|
4
|
0,431 ;0,700;1,068; 1,104
|
4-12(1,140)
|
11 и 7
|
| 11
|
0,408 ;0,182;0,611; 0,652; 0,773;0,779; 0,805; 0,881; 1,104
|
11-7(0,993)
|
Результатом этих действий выступает построение древа. Данное древо изображено на рисунке 3,8.
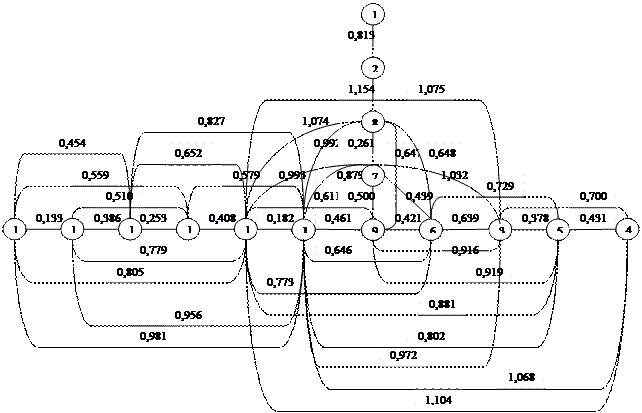
Рис.3,8 Древо взаимосвязей
Из рисунка видно, что этот метод учел все связи объектов, а не отбросил как два предыдущих «ненужную» информацию и больше всего связей имеют объекты 10 и 11(12 связей), а меньше всего 1 и 2(1 и 2 связи соответственно). Что говорит о том, что 1 и 2 объекты аномальны.
Разбиение древа осуществляется путем выбора пороговой величины h. В данном случае она равна 0,435(получаются «нормальные» плеяды). Значит, удаляем все связи больше данного числа. В результате получаем «нормальные» плеяды(рис 3,9):
Рис.3,9 «Нормальные» плеяды.
Замечание
: периодизация с помощью метода корреляционных плеяд выделила точно такие же периоды развития, что и периодизация с помощью метода дендритов.
Тогда названия периодов будут аналогичными:
I
период 1997,1998 –
выше среднего уровень здоровья
II
период 1993-1995 -
средний уровень здоровья
III
период 1996,1999–
ниже среднего уровень здоровья
IV
период 2000-2005 –
критический или низкий уровень здоровья
А интерпретация получается следующая I период –это низкое здоровье населения но для России это максимально достигнутое значение за рассматриваемый период(1991-2005) и тому подобное.
Заключение.
Периодизация – разбиение динамических рядов на интервалы однокачественного развития.
Периодизация, с одной стороны, дает важную информацию о процессе, с другой- закладывает основы для последующего анализа динамики, так как обеспечивает возможность применения методов многомерной статистики; адекватное их использование возможно лишь в однородных сферах. Однако, в отличие от типологической группировки, периодизация исключительно редко используется в расчетах, соответственно и теория ее применения практически не разработана, нет устоявшихся корректных статистических методов ее реализации. Причин данной ситуации несколько, и основная заключается в противоречивости различных условий применения алгоритмов корреляционно-регрессионного анализа(КРА) в рядах динамики.
Однородными периодами примято считать временной промежуток, соответствующий одной из следующих ситуаций: равенство уровней ряда; равенство абсолютных приростов; равенство вторых абсолютных разностей;
равенство цепных темпов роста.
Прежде чем прибегнуть к помощи методов сравнительного анализа, необходимо выполнить определенные преобразования: составить матрицу наблюдений, стандартизовать или нормировать данных, рассчитать матрицу расстояний или матрицу коэффициентов корреляции.
Недостатком метода шаров является то, что существует потенциальная возможность разделить действительно однородные объекты(однородность это структурное сходство).
Положительной чертой методов дендрита и корреляционных плеяд является их относительная простота. Но самым большим достоинством этих двух методов является инвариантность их техники относительно характера исходных данных. Эти методы успешно реализуются как на различных метриках в случае использования метода дендритов, так и на матрицах коэффициентов взаимной сопряженности, либо на теоретико- информационных мер связи в том случае, если будет применен метод корреляционных плеяд. Более того , как техника метода дендритов применима к матрицам связи, так и метод корреляционных плеяд можно реализовать на матрицах расстояний.
Преимуществом также метода корреляционных плеяд является то, что он учитывает все связи он не отбрасывает как два предыдущих метода «не нужную информацию».
Недостатком методов(особенно корреляционных плеяд) является их неформализованность, что затрудняет применение вычислительной техники, т.е он становится очень трудоемким при достаточно большом числе объектов.
Изменение уровня здоровья в России в основном протекает в рамках очень низких показателей, что может привести к еще более сильному ухудшению здоровья. Стоит надеяться на то, что нацпроект здоровье, принятый 21 декабря 2005 года, изменит эту ситуацию.
Можно также отметить, что все методы периодизации выделили два аномальных, переходных года 1991 и 1992.Метод корреляционных плеяд наглядно показал на сколько сильно взаимосвязаны объекты данной совокупности(древо взаимосвязей).
Используя эти методы, мы всегда можем получить информацию об однородности числовых данных, определенных локальных сгущениях и разреженности. Благодаря этим методам можно выяснить, каким образом размещаются точки объекты в многомерном пространстве их взаимосвязи.
Исследования в данной тематике будут продолжаться , так как данные методы несут эмпирический характер.
Список литературы.
1) Плюта В: Сравнительный многомерный анализ в экономических исследованиях: Методы таксономии и факторного анализа/ Пер. с пол. В.В. Иванова; Науч. ред. В.М. Жуковский . – М .: Статистика, 1980. – 151с.
2) Плюта В: Сравнительный многомерный анализ в экономическом моделировании/ Пер. с польск. В.В. Иванова. – М .: Финансы и статистика, 1989. – 175с.
3) Глинский В.В. Статистические методы прогнозирования социально-экономических процессов.- Новосибирск,1992. 42 с.
4) Аркадьев А.Г., Браверман Э.М. Обучение машин классификации объектов. М., Наука,1971,192с.
5) Статистика: учебное пособие/ И.Г. Переяслова, Е.Б. Колбачев, О.Г. Переяслова. – изд.2-е.- Ростов н/Д.:Феникс,2005. -282 с.
6) Афанасьев В.Н., Юзбашев М.М. Анализ временных рядов и прогнозирование: учебник.- М.: Финансы и статистика,2001. -228 с.
7) Глинский В.В., Ионин И.Г. Статистический анализ: учебное пособие. 3-е изд., пепераб. И доп. – М.:ИНФРА-М; Новосибирск: Сибирское соглашение,2002.- 241с.
8) Дубров А.М., Мхиторян В.С., Трошин Л.И. Многомерные статистические методы : Учебник. – М.: Финансы и статистика, 1998. -352с.
9) Статистический словарь 1996г. Москва. Фмнстатинформ. Главный редактор Юрков Ю.А.
10) Российский статистический ежегодник 2006: Стат.сб/ Росстат.-М., 2006. 806 с.
11) Российский статистический ежегодник: Стат.сб/ Госкомстат России.- М.,2001. – 679 с.
12) Россия в цифрах. 2007: Крат. Стат. Сб/ Росстат – М., 2007,-494с.
[1]
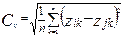
|