Задание 1.
С целью изучения общественного мнения по вопросу содержания и качества телевизионных программ принято решение провести опрос населения.
1) Определите объект наблюдения, единицу наблюдения, отчетную единицу.
2) Какие признаки следует регистрировать при проведении данного наблюдения?
3) Укажите, к какому виду относится данное наблюдение по времени, охвату и способу получения данных.
Решение:
Статистическое наблюдение выступает как один из главных методов статистики и как одна из важнейших стадий статистического исследования. Под статистическими данными (информацией) понимают совокупность количественных характеристик социально-экономических явлений и процессов, полученных в результате статистического наблюдения, их обработки или соответствующих расчетов.
Цель наблюдения
. Статистические наблюдения чаще всего преследуют практическую цель - получение достоверной информации для выявления закономерностей развития явлений и процессов. В нашем случае, целью было получение данных о содержания телевизионных программ.
Задача наблюдения
– проанализировать потребности населения в содержании телевизионных программ.
Объект наблюдения
– жители города N.
Для формирования выборочной совокупности из общего числа жителей можно применить типическую выборку, которая предполагает предварительное разделение генеральной совокупности на однородные группы, которые образуются посредством специально проведенной типической, группировки единиц генеральной совокупности. Единицей измерения в данном случае будет покупатель магазина. Численность покупателей можно разделить на мужчин и женщин, выделяя их по возрасту и другим признакам и в каждой полученной группе провести отбор, пропорциональный численности групп.
Для получения дополнительных сведений о зрителях в выборочной совокупности можно провести анкетирование. Определяя необходимый круг вопросов надо исходить из цели анкетирования - получения дополнительной информации для улучшения качества телепрограмм. Таким образом, в анкету следует включить вопросы о возрасте, цене, тематике и продолжительности программ. Следует выяснить по результатам анкетирования численность зрителей удовлетворенных имеющимся предложением и неудовлетворенных. Распространив результаты выборочного наблюдения на генеральную совокупность, можно определить особенности спроса на телепрограммы. Если включить в анкету вопрос о требованиях к тематике, то можно определить оптимальное содержание программ.
Реклама

Задание 2.
При 5%-ном выборочном обследовании страховых организаций получены следующие данные:
№
организации
|
Количество страховых случаев |
Размер страховых выплат, д.е. |
Число договоров страхования |
Размер страховых взносов, д.е. |
| 1 |
5 |
25000 |
100 |
50000 |
| 2 |
4 |
17955 |
95 |
42750 |
| 3 |
6 |
31680 |
110 |
52800 |
| 4 |
4 |
10800 |
85 |
41650 |
| 5 |
7 |
36344 |
118 |
51920 |
| 6 |
3 |
21385 |
65 |
30550 |
| 7 |
8 |
54600 |
140 |
84000 |
| 8 |
3 |
13920 |
60 |
34800 |
| 9 |
3 |
10700 |
70 |
36400 |
| 10 |
4 |
11540 |
82 |
40180 |
| 11 |
5 |
17437 |
94 |
49820 |
| 12 |
4 |
12480 |
78 |
39000 |
| 13 |
3 |
12300 |
63 |
30240 |
| 14 |
3 |
10900 |
87 |
43065 |
| 15 |
5 |
9900 |
96 |
48480 |
| 16 |
9 |
47328 |
136 |
78880 |
| 17 |
5 |
31860 |
120 |
70800 |
| 18 |
5 |
20608 |
115 |
64400 |
| 19 |
4 |
16800 |
112 |
67200 |
| 20 |
7 |
31230 |
128 |
78080 |
На основе приведенных данных:
1)проведите группировку страховых организаций по числу договоров страхования, выделив четыре группы с равными интервалами;
2)по каждой выделенной группе и по совокупности в целом рассчитайте:
· число страховых организаций,
· среднее число договоров страхования на одну организацию,
· размер страховых взносов по группе и в среднем на одну организацию,
· количество страховых случаев по группе и в среднем на одну организацию.
Результаты группировки представьте в таблице. Проанализируйте показатели таблицы. Установите характер связи между: числом договоров и количеством страховых случаев. Для измерения тесноты связи между этими показателями исчислите эмпирическое корреляционное отношение. Сделайте выводы.
Решение:
Проведем группировку страховых организаций по числу страховых случаев и построим интервальный ряд распределения.
Для построения интервального вариационного ряда, характеризующего распределение страховых организаций по числу договоров страхования, необходимо вычислить величину и границы интервалов ряда.
При построении ряда с равными интервалами величину интервала h
определяем по формуле
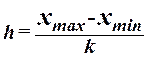 ,
,
где 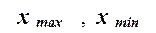 – наибольшее и наименьшее значения признака в исследуемой совокупности, k
-
число групп интервального ряда.
– наибольшее и наименьшее значения признака в исследуемой совокупности, k
-
число групп интервального ряда.
Определение величины интервала по формуле при заданных k
= 4, xmax
= 140, xmin
= 60:
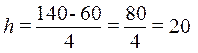
При h
= 20 границы интервалов ряда распределения имеют следующий вид:
| Номер группы |
Нижняя граница,
млн руб.
|
Верхняя граница,
млн руб.
|
| 1 |
60 |
80 |
| 2 |
80 |
100 |
| 3 |
100 |
120 |
| 4 |
120 |
140 |
Для построения интервального ряда необходимо подсчитать число страховых организаций, входящих в каждую группу (частоты групп). При этом возникает вопрос, в какую группу включать единицы совокупности, у которых значения признака выступают одновременно и верхней, и нижней границами смежных интервалов. Отнесение таких единиц к одной из двух смежных групп осуществляем по принципу полуоткрытого интервала [ ). Т.к. при этом верхние границы интервалов не принадлежат данным интервалам, то соответствующие им единицы совокупности включаются не в данную группу, а в следующую. В последний интервал включаются и нижняя, и верхняя границы.
Построим рабочую таблицу:
Реклама

| Группы организаций по числу страховых договоров |
N организации |
Количество страховых случаев |
Размер страховых выплат, д.е. |
Число договоров страхования |
Размер страховых взносов, д.е. |
| 60-80 |
8 |
3 |
13920 |
60 |
34800 |
| 13 |
3 |
12300 |
63 |
30240 |
| 6 |
3 |
21385 |
65 |
30550 |
| 9 |
3 |
10700 |
70 |
36400 |
| 12 |
4 |
12480 |
78 |
39000 |
| Итого |
5 |
16 |
70785 |
336 |
170990 |
| 80-100 |
10 |
4 |
11540 |
82 |
40180 |
| 4 |
4 |
10800 |
85 |
41650 |
| 14 |
3 |
10900 |
87 |
43065 |
| 11 |
5 |
17437 |
94 |
49820 |
| 2 |
4 |
17955 |
95 |
42750 |
| 15 |
5 |
9900 |
96 |
48480 |
| Итого |
6 |
25 |
78532 |
539 |
265945 |
| 100-120 |
1 |
5 |
25000 |
100 |
50000 |
| 3 |
6 |
31680 |
110 |
52800 |
| 19 |
4 |
16800 |
112 |
67200 |
| 18 |
5 |
20608 |
115 |
64400 |
| 5 |
7 |
36344 |
118 |
51920 |
| Итого |
5 |
27 |
130432 |
555 |
286320 |
| 120-140 |
17 |
5 |
31860 |
120 |
70800 |
| 20 |
7 |
31230 |
128 |
78080 |
| 16 |
9 |
47328 |
136 |
78880 |
| 7 |
8 |
54600 |
140 |
84000 |
| Итого |
4 |
29 |
165018 |
524 |
311760 |
| ВСЕГО |
20 |
97 |
444767 |
1954 |
1035015 |
На основе рабочей таблицы составим аналитическую:
| Группы организаций по числу страховых договоров |
N организации |
Количество страховых случаев |
Размер страховых выплат, д.е. |
Число договоров страхования |
Размер страховых взносов, д.е. |
| Всего |
На 1 орг. |
Всего |
На 1 орг. |
Всего |
На 1 орг. |
Всего |
На 1 орг. |
| 60-80 |
5 |
16 |
3,20 |
70785 |
14157,0 |
336 |
67,20 |
170990 |
34198,0 |
| 80-100 |
6 |
25 |
4,17 |
78532 |
13088,7 |
539 |
89,83 |
265945 |
44324,2 |
| 100-120 |
5 |
27 |
5,40 |
130432 |
26086,4 |
555 |
111,00 |
286320 |
57264,0 |
| 120-140 |
4 |
29 |
7,25 |
165018 |
41254,5 |
524 |
131,00 |
311760 |
77940,0 |
| ВСЕГО |
20 |
97 |
4,85 |
444767 |
22238,4 |
1954 |
97,70 |
1035015 |
51750,8 |
Таким образом, можно сделать вывод, что размер страховых выплат на одну организацию, число договоров страхования на одну организацию, размер страховых взносов на одну организацию растут пропорционально росту числа договоров страхования.
Установим характер связи между числом договоров и количеством страховых случаев. Для измерения тесноты связи между этими показателями исчислим эмпирическое корреляционное отношение.
Для измерения тесноты связи между факторным и результативным признаками рассчитывают специальные показатели – эмпирический коэффициент детерминации 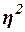 и эмпирическое корреляционное отношение и эмпирическое корреляционное отношение 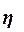 . .
Эмпирический коэффициент детерминации 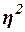 оценивает, насколько вариация результативного признака Y
объясняется вариацией фактора Х
(остальная часть вариации Y
объясняется вариацией прочих факторов). Показатель оценивает, насколько вариация результативного признака Y
объясняется вариацией фактора Х
(остальная часть вариации Y
объясняется вариацией прочих факторов). Показатель 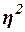 рассчитывается как доля межгрупповой дисперсии в общей дисперсии по формуле рассчитывается как доля межгрупповой дисперсии в общей дисперсии по формуле
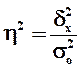 , ,
где 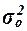 – общая дисперсия признака Y
, – общая дисперсия признака Y
,
 – межгрупповая (факторная) дисперсия признака Y
. – межгрупповая (факторная) дисперсия признака Y
.
Значения показателя 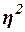 изменяются в пределах изменяются в пределах . При отсутствии корреляционной связи между признаками Х
и Y
имеет место равенство . При отсутствии корреляционной связи между признаками Х
и Y
имеет место равенство 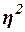 =0
, а при наличии функциональной связи между ними - равенство =0
, а при наличии функциональной связи между ними - равенство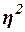 =1
. =1
.
Общая дисперсия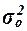 характеризует вариацию результативного признака, сложившуюся под влиянием всех действующих на Y
факторов (систематических и случайных). Этот показатель вычисляется по формуле характеризует вариацию результативного признака, сложившуюся под влиянием всех действующих на Y
факторов (систематических и случайных). Этот показатель вычисляется по формуле
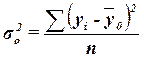 , ,
где yi
– индивидуальные значения результативного признака;
 – общая средняя значений результативного признака; – общая средняя значений результативного признака;
n
– число единиц совокупности.
Общая средняя  вычисляется как средняя арифметическая простая по всем единицам совокупности: вычисляется как средняя арифметическая простая по всем единицам совокупности:
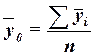
Расчет 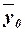 по формуле: по формуле:
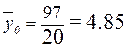
Для расчета общей дисперсии 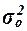 применяется вспомогательная таблица. применяется вспомогательная таблица.
Вспомогательная таблица для расчета общей дисперсии
| N организации |
Количество страховых случаев |
 |
 |
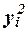 |
| 1
|
2
|
3
|
4
|
5
|
| 1 |
5 |
0,15 |
0,0225 |
25 |
| 2 |
4 |
-0,85 |
0,7225 |
16 |
| 3 |
6 |
1,15 |
1,3225 |
36 |
| 4 |
4 |
-0,85 |
0,7225 |
16 |
| 5 |
7 |
2,15 |
4,6225 |
49 |
| 6 |
3 |
-1,85 |
3,4225 |
9 |
| 7 |
8 |
3,15 |
9,9225 |
64 |
| 8 |
3 |
-1,85 |
3,4225 |
9 |
| 9 |
3 |
-1,85 |
3,4225 |
9 |
| 10 |
4 |
-0,85 |
0,7225 |
16 |
| 11 |
5 |
0,15 |
0,0225 |
25 |
| 12 |
4 |
-0,85 |
0,7225 |
16 |
| 13 |
3 |
-1,85 |
3,4225 |
9 |
| 14 |
3 |
-1,85 |
3,4225 |
9 |
| 15 |
5 |
0,15 |
0,0225 |
25 |
| 16 |
9 |
4,15 |
17,2225 |
81 |
| 17 |
5 |
0,15 |
0,0225 |
25 |
| 18 |
5 |
0,15 |
0,0225 |
25 |
| 19 |
4 |
-0,85 |
0,7225 |
16 |
| 20 |
7 |
2,15 |
4,6225 |
49 |
| Итого |
97 |
58,55 |
529 |
Расчет общей дисперсии по формуле:
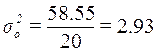
Межгрупповая дисперсия
 измеряет систематическую вариацию
результативного признака, обусловленную влиянием признака-фактора Х
(по которому произведена группировка). Воздействие фактора Х
на результативный признак Y
проявляется в отклонении групповых средних измеряет систематическую вариацию
результативного признака, обусловленную влиянием признака-фактора Х
(по которому произведена группировка). Воздействие фактора Х
на результативный признак Y
проявляется в отклонении групповых средних  от общей средней от общей средней 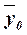 . .
Показатель  вычисляется по формуле вычисляется по формуле
 , ,
где 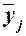 –групповые средние, –групповые средние,
 – общая средняя, – общая средняя,
 –число единиц в j-ой группе, –число единиц в j-ой группе,
k
– число групп.
Для расчета межгрупповой дисперсии  строится вспомогательная таблица При этом используются групповые средние значения строится вспомогательная таблица При этом используются групповые средние значения 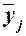 . .
Вспомогательная таблица для расчета межгрупповой дисперсии
| Группы организаций по числу страховых договоров |
Число организаций,

|
Среднее значение  в группе в группе |
 |
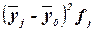 |
| 1
|
2
|
3
|
4
|
5
|
| 40 – 90 |
5 |
3,20 |
-1,65 |
13,61 |
| 90 – 140 |
6 |
4,17 |
-0,68 |
2,80 |
| 140 – 190 |
5 |
5,40 |
0,55 |
1,51 |
| 190 – 240 |
4 |
7,25 |
2,40 |
23,04 |
| Итого |
20 |
4,85 |
40,97 |
Расчет межгрупповой дисперсии  по формуле: по формуле:
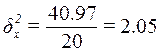
Расчет эмпирического коэффициента детерминации 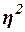 по формуле: по формуле:
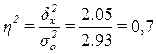 или 70% или 70%
Вывод.
70% вариации страховых случаев обусловлено вариацией числа страховых договоров, а 30% – влиянием прочих неучтенных факторов.
Эмпирическое корреляционное отношение
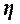 оценивает тесноту связи между факторным и результативным признаками и вычисляется по формуле оценивает тесноту связи между факторным и результативным признаками и вычисляется по формуле
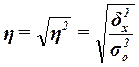
Значение показателя изменяются в пределах 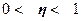 . Чем ближе значение . Чем ближе значение 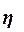 к 1, тем теснее связь между признаками. Для качественной оценки тесноты связи на основе к 1, тем теснее связь между признаками. Для качественной оценки тесноты связи на основе 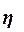 служит шкала Чэддока: служит шкала Чэддока:
Шкала Чэддока
| h
|
0,1 – 0,3 |
0,3 – 0,5 |
0,5 – 0,7 |
0,7 – 0,9 |
0,9 – 0,99 |
Характеристика
силы связи
|
Слабая |
Умеренная |
Заметная |
Тесная |
Весьма тесная |
Расчет эмпирического корреляционного отношения 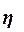 по формуле: по формуле:
 или 83,7% или 83,7%
Вывод
. Согласно шкале Чэддока связь между числом страховых случаев и числом страховых договоров является тесной.
Задание 3.
Имеются следующие распределения работников предприятия по стажу работы:
| Стаж работы, лет |
Численность работников |
| Мужчины |
Женщины |
| 1 |
10 |
5 |
| 2 |
12 |
7 |
| 3 |
28 |
8 |
| 4 |
20 |
9 |
| 5 |
20 |
16 |
| 6 |
12 |
22 |
| 7 |
5 |
17 |
| 8 |
3 |
16 |
| Итого: |
110 |
100 |
Определите:
· средний стаж работы мужчин, женщин, всех работников предприятия (укажите взаимосвязь между исчисленными показателями);
· модальное и медианное значение признака для мужчин, женщин, всех работников предприятия;
· абсолютные и относительные показатели вариации стажа работы для мужчин.
Решение:
Определим средний стаж работы по формуле средней взвешенной:
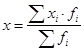 , где х – стаж работы, лет; f – численность работников, чел. , где х – стаж работы, лет; f – численность работников, чел.
Построим таблицу для расчета:
| Стаж работы, лет (x) |
Численность работников |
x*f1
|
x*f2
|
x*f3
|
| Мужчины (f1
) |
Женщины (f2
) |
Всего (f3
) |
| 1 |
10 |
5 |
15 |
10 |
5 |
15 |
| 2 |
12 |
7 |
19 |
24 |
14 |
38 |
| 3 |
28 |
8 |
36 |
84 |
24 |
108 |
| 4 |
20 |
9 |
29 |
80 |
36 |
116 |
| 5 |
20 |
16 |
36 |
100 |
80 |
180 |
| 6 |
12 |
22 |
34 |
72 |
132 |
204 |
| 7 |
5 |
17 |
22 |
35 |
119 |
154 |
| 8 |
3 |
16 |
19 |
24 |
128 |
152 |
| Итого |
110 |
100 |
210 |
429 |
538 |
967 |
Получаем:
· для мужчин 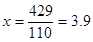 года; года;
· для женщин 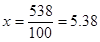 года; года;
· для всех 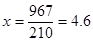 года. года.
Взаимосвязь исчисленных показателей покажем выражением:
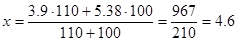 года. года.
Так как, мы имеем дело с дискретным рядом, то конкретное значение моды будет являться вариант с наибольшей частотой:
· для мужчин 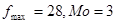 года; года;
· для женщин 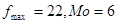 лет; лет;
· для всех  лет. лет.
Конкретное значение медианы для дискретного ряда рассчитываем по формуле:
 , ,
где хМе
– нижняя граница медианного интервала,
h
– величина медианного интервала,
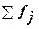 – сумма всех частот, – сумма всех частот,
fМе
– частота медианного интервала,
SMе-1
– кумулятивная (накопленная) частота интервала, предшествующего медианному.
Для расчета медианы необходимо, прежде всего, определить медианный интервал, для чего используются накопленные частоты (или частости). Так как медиана делит численность ряда пополам, она будет располагаться в том интервале, где накопленная частота впервые равна
полусумме всех частот 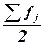 или превышает ее (т.е. все предшествующие накопленные частоты меньше этой величины). или превышает ее (т.е. все предшествующие накопленные частоты меньше этой величины).
Расчет значения медианы по формуле:
· для мужчин 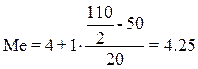 года; года;
· для женщин 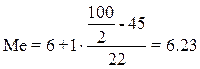 года; года;
· для всех 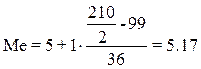 лет. лет.
Определим абсолютные и относительные показатели вариации стажа работы для мужчин:
· абсолютные - размах вариации (R), среднее линейное отклонение (d), среднее квадратическое отклонение (σ), дисперсию (σ2
).
· относительные - коэффициент осцилляции (VR
), линейный коэффициент вариации (Vd
), коэффициент вариации (Vσ
).
 лет. лет.

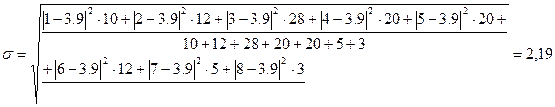 года. года.
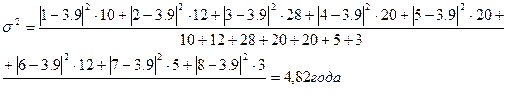
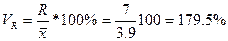

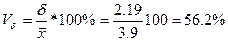
Таким образом, средний стаж у мужчин составил 3,9 года, а среднее отклонение от средней 2,19 года или 56,2%.
Задание 4.
Имеются следующие данные о жилищном фонде (общей площади жилищ) по состоянию на конец года:
| 1996 |
1997 |
1998 |
1999 |
2000 |
| Жилищный фонд, млн м ² |
2425 |
2449 |
2492 |
2546 |
2600 |
Для анализа динамики жилищного фонда рассчитайте за 1996-2000 гг. следующие показатели:
1) средний уровень ряда;
2) абсолютные приросты (цепные, базисные, средние);
3) темпы роста и прироста (цепные, базисные, средние);
4) абсолютное значение одного процента прироста (по годам).
Проведите аналитическое выравнивание ряда динамики. Изобразите фактические и выравненные данные на графике. Определите предполагаемое значение изучаемого показателя (жилищного фонда) на 2002г. (разными методами).
Решение:
Средний уровень ряда определим по формуле средней хронологической:
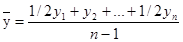 , где у – значение показателя по годам. , где у – значение показателя по годам.
Получаем:
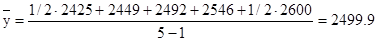 м.кв. м.кв.
Абсолютный прирост выражает абсолютную скорость изменения ряда динамики и определяется как разность между данным уровнем и уровнем, принятым за базу сравнения.
Абсолютный прирост (базисный)
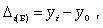 где yi - уровень сравниваемого периода; y0 - уровень базисного периода. где yi - уровень сравниваемого периода; y0 - уровень базисного периода.
Абсолютный прирост с переменной базой (цепной), который называют скоростью роста,
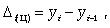 где yi - уровень сравниваемого периода; yi-1 - уровень предшествующего периода. где yi - уровень сравниваемого периода; yi-1 - уровень предшествующего периода.
Коэффициент роста Ki определяется как отношение данного уровня к предыдущему или базисному, показывает относительную скорость изменения ряда. Если коэффициент роста выражается в процентах, то его называют темпом роста.
Коэффициент роста базисный
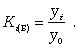
Коэффициент роста цепной
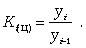
Темп роста
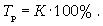
Темп прироста ТП определяется как отношение абсолютного прироста данного уровня к предыдущему или базисному.
Темп прироста базисный
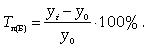
Темп прироста цепной
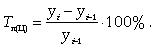
Абсолютное значение одного процента прироста Ai . Этот показатель служит косвенной мерой базисного уровня. Представляет собой одну сотую часть базисного уровня, но одновременно представляет собой и отношение абсолютного прироста к соответствующему темпу роста.
Данный показатель рассчитывают по формуле

Расчет представим в виде таблицы:
| Годы |
1996 |
1997 |
1998 |
1999 |
2000 |
| Жилищный фонд,м 2
|
2425 |
2449 |
2492 |
2546 |
2600 |
| Абсолютный прирост |
цепной |
- |
24 |
43 |
54 |
54 |
| базисный |
- |
24 |
67 |
121 |
175 |
| Коэффициент роста |
цепной |
- |
1,010 |
1,018 |
1,022 |
1,021 |
| базисный |
- |
1,010 |
1,028 |
1,050 |
1,072 |
| Темп роста |
цепной |
- |
101,0 |
101,8 |
102,2 |
102,1 |
| базисный |
- |
101,0 |
102,8 |
105,0 |
107,2 |
| Темп прироста |
цепной |
- |
1,0 |
1,8 |
2,2 |
2,1 |
| базисный |
- |
1,0 |
2,8 |
5,0 |
7,2 |
| Абсолютное значение одного процента прироста |
- |
24,25 |
24,49 |
24,92 |
25,46 |
Определим средний абсолютный прирост по формуле:
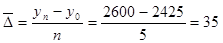 м.кв. м.кв.
Средний годовой темп роста определим по формуле:
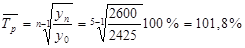
Средний годовой темп прироста определим по формуле:
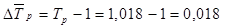 или 1,8%. или 1,8%.
Важнейшим способом количественного выражения общей тенденции изменения уровней динамического ряда является аналитическое выравнивание ряда динамики, которое позволяет получить описание плавной линии развития ряда. При этом эмпирические уровни заменяются уровнями, которые рассчитываются на основе определенной кривой, где уравнение рассматривается как функция времени. Вид уравнения зависит от конкретного характера динамики развития. Его можно определить как теоретически, так и практически. Теоретический анализ основывается на рассчитанных показателях динамики. Практический анализ - на исследовании линейной диаграммы.
Наш ряд можно охарактеризовать линией 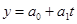
Построим систему уравнений:

Определим параметры а, для чего построим таблицу:
| Год |
У |
t |
∑Yt |
∑t2
|
Y* |
| 1996 |
2425 |
-2 |
-4850 |
4 |
2413 |
| 1997 |
2449 |
-1 |
-2449 |
1 |
2457,7 |
| 1998 |
2492 |
0 |
0 |
0 |
2502,4 |
| 1999 |
2546 |
1 |
2546 |
1 |
2547,1 |
| 2000 |
2600 |
2 |
5200 |
4 |
2591,8 |
| Всего |
12512 |
0 |
447 |
10 |
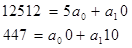
Получаем
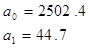

Таким образом, основная тенденция ряда динамики положительна, так как а1
>0.
Построим графики:
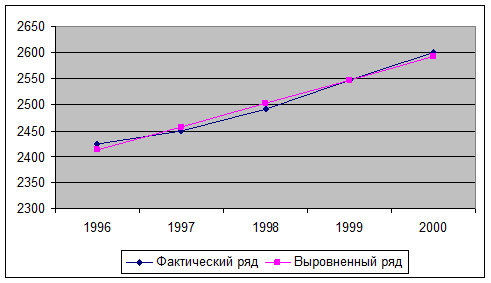
Определим предполагаемое значение изучаемого показателя (обеспеченности граждан жильем) на 2002 г.
С помощью среднегодового темпа роста:
 м.кв. м.кв.
С помощью среднегодового абсолютного прироста:
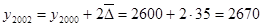 м.кв. м.кв.
С помощью математического уравнения:
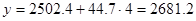 м.кв. м.кв.
Задание 5.
Имеются данные выборочного обследования весенней торговли фруктами на продовольственных рынках:
| Фрукты |
Цена за кг, д.е. |
Продано, кг |
| Март |
Апрель |
Март |
Апрель |
| Яблоки |
25 |
30 |
860 |
810 |
| Мандарины |
30 |
35 |
750 |
650 |
| Лимоны |
30 |
40 |
350 |
300 |
| Груши |
25 |
35 |
1450 |
1000 |
Определите:
1) индивидуальные индексы цен, физического объема товарооборота и стоимости реализованных фруктов;
2) общие индексы цен, физического объема товарооборота и стоимости реализованных фруктов;
3) абсолютное изменение стоимости реализованных фруктов;
4) абсолютную величину экономии или перерасхода денежных средств покупателей от изменения цен;
5) абсолютное изменение стоимости реализованных фруктов за счет изменения физического объема товарооборота.
Решение:
Определим
индивидуальные индексы цен, физического объема товарооборота и стоимости реализованных фруктов.
Индивидуальные индексы цен определим по формуле: 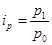 , где р – цена за единицу. , где р – цена за единицу.
Индивидуальные индексы физического объема товарооборота определим по формуле: 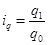 , где q – продано единиц товара. , где q – продано единиц товара.
Индивидуальные индексы стоимости реализованных фруктов определим по формуле: 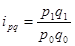
Расчет приведем в таблице:
| Фрукты |
Цена за кг, д.е. |
ip |
Продано, кг |
iq |
ipq |
| март |
апрель |
март |
апрель |
| Яблоки |
25 |
30 |
1,200 |
860 |
810 |
0,942 |
1,130 |
| Мандарины |
30 |
35 |
1,167 |
750 |
650 |
0,867 |
1,011 |
| Лимоны |
30 |
40 |
1,333 |
350 |
300 |
0,857 |
1,143 |
| Груши |
25 |
35 |
1,400 |
1450 |
1000 |
0,690 |
0,966 |
Общий индекс цен определим по формуле:
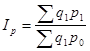
Получаем:
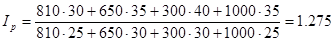
Общий индекс физического объема товарооборота определим по формуле:
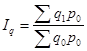
Получаем:
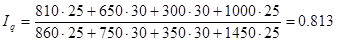
Общий индекс стоимости реализованных фруктов определим по формуле:
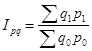
Получаем:
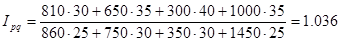
Абсолютное изменение стоимости реализованных фруктов определим по формуле:
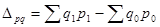
Получаем:
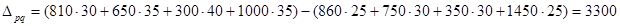 д.е. д.е.
Абсолютную величину перерасхода денежных средств покупателей от изменения цен определим по формуле:
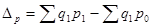
Получаем:
 д.е. д.е.
Абсолютное изменение стоимости реализованных фруктов за счет изменения физического объема товарооборота определим по формуле:
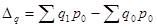
Получаем:
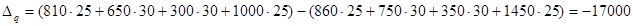 д.е. д.е.
Таким образом, товарооборот вырос в 1,036 раза (+3,6%) или на 3300д.е., в том числе за счет изменения цены в среднем в 1,275 раза (+27,5%) или на 20300 д.е., а за счет изменения физического объема сократился в 0,813 раза (+18,7%) или на 17000 д.е.
Список используемой литературы:
1. Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник / Под ред. И.И.Елисеевой. - М.: Финансы и статистика, 1998.
2. Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики. - М.: ИНФРА-М, 1996.
3. Курс социально-экономической статистики: Учебник для вузов / Под ред. М.Г. Назарова, - М.: Финстатинформ, ЮНИТИ-ДАНА, 2000.
4. Лапуста М.Г., Старостин Ю.Л. Малое предпринимательство. - М.: ИНФРА-М, 1997.
5. Муравьев А.И., Игнатьев А.М., Крутик А.Б. Малый бизнес: экономика, организация, финансы: Учеб. пособие для вузов. - 2-е изд., перераб. и доп. - СПб.: Издательский дом «Бизнес-пресса», 1999.
6. Салин В.Н., Шпаковская Е.П. Социально-экономическая статистика: Учебник. - М.: Юрист, 2001.
7. Теория статистики: Учебник. - 3-е изд., перераб. / Под ред. Р.А. Шмойловой. - М.: Финансы и статистика, 1999.
8. Экономическая статистика / Под ред. Ю.Н. Иванова. - М.: ИНФРА-М, 1999.
|