Міністерство освіти і науки України
Курсова робота:
"Програмування трьохмірної графіки та анімації засобами Turbo Pascal
"
ЗМІСТ
ВСТУП
РОЗДІЛ І. МАТЕМАТИЧНЕ МОДЕЛЮВАННЯ ТРЬОХМІРНОЇ ГРАФІКИ ТА АНІМАЦІЇ
1.1 Операції над векторами й матрицями
1.2 Використання проекцій
1.3 Алгоритми видалення невидимих ребер та граней
1.4 Методи програмування динамічних зображень
РОЗДІЛ ІІ. ПРАКТИЧНА РЕАЛІЗАЦІЯ 3D ОБ’ЄКТІВ ТА ДИНАМІЧНИХ ПОДІЙ
2.1 Модуль обробки 3d об’єктів Graph3d
2.2 Відображення об’ємних фігур в різних проекціях
2.3 Побудова поверхонь
2.4 Відсікання невидимих ліній, використання модуля Graph3d
ВИСНОВКИ
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
ВСТУП
Комп’ютерна графіка з’явилась достатньо давно – вже у 60-х минулого століття існували повноцінні програми роботи з графікою. Сьогодні прийнято користуватися термінами "комп’ютерна графіка" і "комп’ютерна анімація". Поняття "комп’ютерна графіка" об’єднує всі види робот зі статичними зображеннями, "комп’ютерна анімація" має справи з зображеннями, які динамічно змінюються [21].
Сучасний етап розвитку технологій обумовив швидкий ріс графічних додатків, що використовують технологію трьохвимірного відображення. Це і тривимірне телебачення, тривимірні програми моделювання різноманітних пристроїв, деталей. Тривимірність швидко увійшла в наше життя у вигляді мультфільмів, фільмів із героями створеними у редакторах об’ємних фігур. Іграшки на даний час все більше і більше вражають нас своєю реалістичністю, і почасти дуже важко знайти різницю між реальністю і вигадкою, реалізованою на екранах монітора і телевізора [24].
Розвитку трьохмірного графічного проектування, в першу чергу передувало створення нових потужних процесорів, відеокарт та іншого апаратного забезпечення, що дозволяло швидше обробляти більші масиви даних, та відображення їх у реальному часі. Також із часом змінилися програмні засоби, які дозволяли прискорити обробку, винайшли більш швидкі алгоритми роботи, в чомусь відмовилися від несуттєвого акцентуючи увагу на основному.
На даний час основними є дві бібліотеки для роботи із графікою, це бібліотека DirectX та OpenGL. Хоча вони і по різному реалізовані, виконують практично ідентичні функції. Програмування 3d-графіки з їх допомогою значно полегшується, необхідно знати, звичайно, основні команди, поняття і вміти ними користуватися. Проте вони не надають учням основних понять у програмуванні. Так, вони служать в певному роді графічним двигуном, що обробляє дані, проте не надає відповіді, як же проходить перехід від 3d до 2d координат, яким чином відбувається обрахунок нових координат вершини тетраедра при його повороті, як відбувається його масштабування. Всі ці поняття вже закладені у бібліотеці і вважаються зрозумілими [22].
Реклама

Проте, для початківців було б позитивним моментом знати всі ці нюанси, розуміти їх і вміти запрограмувати.
Метою курсової роботи
є надати основні математичні поняття по роботі із 3d-графікою. Вказати шляхи реалізації основних алгоритмів, як то поворот, рух, проекція та відображення та розробити наочні приклади побудови фігур.
Актуальність мети
– випливає із того, що програмування 3d-об’єктів є перспективним напрямком у створенні ігор, технічного ПЗ для створення об’ємних фігур, середовища. Набуття навиків у створенні об’ємної графіки передбачає взаємодію із математичними методами, їх розумінням та можливістю застосування на практиці. Показує зв’язок математики та інформатики.
Об’єкт роботи:
є прикладне програмне забезпечення, середовище програмування та засоби математичного моделювання.
Предмет роботи:
трьохмірна графіка та її алгоритми програмування.
Мета роботи:
є розробка методичного матеріалу, реалізованих програмних продуктів з програмування графічних процесів.
РОЗДІЛ І
. МАТЕМАТИЧНЕ МОДЕЛЮВАННЯ
ТРЬОХМІРНОЇ ГРАФІКИ ТА АНІМАЦІЇ
1.1
Операції над векторами й матрицями
Вирішуючи завдання відображення складних геометричних об’єктів у просторі, необхідно встановити відповідність між точками поверхні геометричного об’єкта й точками плоскої поверхні екрана дисплея. При цьому деякі частині поверхні можуть бути не видимі, можуть відрізнятися умови висвітлення поверхонь, їхні кольори, відбивна здатність і т.п. Все це варто враховувати для побудови реалістичних зображень. Зображення можуть бути нерухомими (статичними) або мінливими в часі (динамічними).
Розглянемо основні математичні поняття, які дозволяють задати положення точки в просторі, ребра об’єкта, його поверхню і властивість поверхні. Положення точки в просторі задається за допомогою координат. Значення координат залежать від вибору системи координат і точки початку її відліку. В прямокутній (декартовій системі) координат положення точки задається трьома числами — координатами x
, y
та z
(Рис. 1.1).
Реклама

Ці координати є компонентами вектора, що йде з початку системи координат у задану точку: 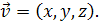
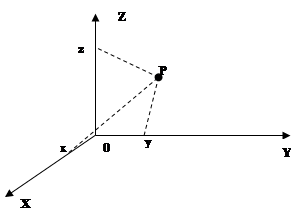
Рис. 1.1. Декартова система координат
У загальному випадку осі системи координат можуть розташовуватися під довільними, хоча й фіксованих кутах одна до іншої. Для практичних розрахунків набагато зручніше коли ці осі розташовані взаємно перпендикулярно. Така система координат називається ортогональної. В ортогональній системі координат проекцією точки 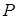 на вісь є єдина точка на осі така, що відрізок прямої, проведеної із цієї точки до точки на вісь є єдина точка на осі така, що відрізок прямої, проведеної із цієї точки до точки 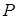 є перпендикулярним до даної осі [17]. є перпендикулярним до даної осі [17].
Таким чином, положення в просторі точки 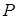 описується її координатами, що записується як описується її координатами, що записується як 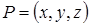 . Взаємне розташування осей в ортогональній системі координат у тривимірному просторі може бути двох видів. Проведемо вісь . Взаємне розташування осей в ортогональній системі координат у тривимірному просторі може бути двох видів. Проведемо вісь 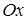 з ліва на право, а вісь з ліва на право, а вісь 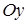 знизу вгору, як показано на Рис. 1.2. знизу вгору, як показано на Рис. 1.2.

Рис. 1.2. Лівостороння й правобічна системи координат
Вісь 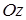 при цьому може проходити як у напрямку від спостерігача в площину листа, так і від площини листа до спостерігача. У першому випадку система координат буде називатися лівої або лівосторонньої, а в другому випадку – правої або правобічної. Існує також легкий спосіб визначення виду системи координат по правій або лівій руці, як показано на Рис. 1.3. Для лівої руки великий, вказівний і середній пальці формують ліву трійку ортогональних векторів. Те ж відноситься і до їхніх циклічних перестановок. при цьому може проходити як у напрямку від спостерігача в площину листа, так і від площини листа до спостерігача. У першому випадку система координат буде називатися лівої або лівосторонньої, а в другому випадку – правої або правобічної. Існує також легкий спосіб визначення виду системи координат по правій або лівій руці, як показано на Рис. 1.3. Для лівої руки великий, вказівний і середній пальці формують ліву трійку ортогональних векторів. Те ж відноситься і до їхніх циклічних перестановок.
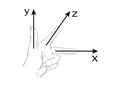
Рис. 1.3. Визначення лівосторонньої системи координат по лівій руці
Будь-яка точка
в 3d програмуванні задається набором з 3-х координат по ортогональним (взаємноперпендикулярним) осях (x, y, z)
відповідно [15].
Точками задаються також координати вершин об’єкта.
Відрізок
- частина прямої, що з’єднує дві точки. Задається координатами кінців. Взаємне положення двох точок також задається вектором, спрямованим з однієї точки в іншу.
Нехай є крапка A
з координатами (Ax, Ay, Az
), і точка B
з координатами (Bx, By, Bz
),тоді вектор з початком у точці A
і кінцем у точці B
є
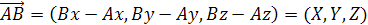 (1.1) (1.1)
Норма (довжина) вектора визначається в такий спосіб:
 . (1.2) . (1.2)
Довжина вектора є корінь суми квадратів його координат, тобто відстань від початку координат до вершини.
Сума
векторів
– це вектор, координати якого є сумою відповідних координат обох векторів:
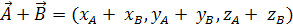 . (1.3) . (1.3)
Різниця
векторів
– це вектор, координати якого є різницею відповідних координат обох векторів.
Добуток
вектора
А
і скаляра а
– це вектор з наступними компонентами:
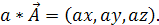 (1.4) (1.4)
Скалярний добуток
двох векторів
– число, що визначається в такий спосіб:
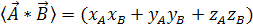 . (1.5) . (1.5)
або
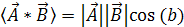 . (1.6) . (1.6)
де b
- кут між векторами.
Проекція вектора на вектор
– це вектор, що має той самий або протилежний напрямок, що й вектор, на який проводиться проектування. Довжина проекції визначається як відстань між підставам і перпендикулярів, проведених з початкової й кінцевої точок проектованого вектора на другий вектор. Проекція вектора А
на вектор В
визначається так:
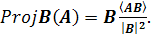 (1.7) (1.7)
Векторний добуток
двох векторів — це вектор, компоненти якого рівні
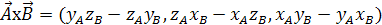 . (1.8) . (1.8)
Векторний добуток спрямований перпендикулярно обом співмножникам.
Перенесенням
називається наступне перетворення:
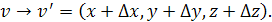 (1.9) (1.9)
Де 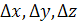 – коефіцієнти перенесення по відповідних осях [15]. – коефіцієнти перенесення по відповідних осях [15].
Матрицею
називають таблицю, елементами якої є числа. Визначено операції додавання й множення матриць. Будемо позначати елемент матриці змінною із двома індексами, що визначають номер рядка й номер стовпця: aij
.
Результат дії матриці А
на вектор С
– теж вектор (позначимо його В
), компоненти якого розраховуються в такий спосіб:
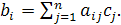 (1.10) (1.10)
Добуток
двох матри
ць А
і С
є матрицею В
, елементи якої обчислюються по формулі
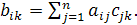 (1.11) (1.11)
Сума
двох матриць
також є матрицею, елементи якої сума додавання відповідних елементів матриць-доданків. При обчисленні суми й добутку матриць повинна дотримуватися відповідність розмірів доданків або співмножників.
Зворотною
стосовно матриці А
, називається матриця А
-1
, що задовольняє умові А-1
A=АА-1
=I
, де I
– одинична матриця, тобто матриця, у якої на головній діагоналі розміщені одиниці (ikk
=1
), а всі інші елементи дорівнюють нулю.
Особливу роль у машинній графіці відіграють перетворення – обертання. При описі поворотів тривимірних об’єктів у комп’ютерній графіці зазвичай використається права система координат. Нехай одиничні вектори 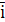 , , 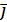 і і 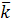 спрямовані вздовж координатних осей 0x
, 0y
і 0z
. У правій системі координат поворот від вектора спрямовані вздовж координатних осей 0x
, 0y
і 0z
. У правій системі координат поворот від вектора 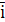 до вектора до вектора 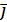 на 900
відповідає повороту гвинта із правим різьбленням, а напрямок вектора на 900
відповідає повороту гвинта із правим різьбленням, а напрямок вектора 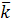 збігається з напрямком переміщення гвинта. Повороти щодо кожної координатної осі на кут а
описуються матрицями повороту: збігається з напрямком переміщення гвинта. Повороти щодо кожної координатної осі на кут а
описуються матрицями повороту:
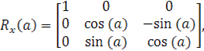 (1.12) (1.12)
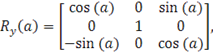 (1.13) (1.13)
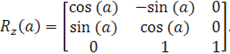 (1.14) (1.14)
Кут повороту вважається позитивним, якщо обертання відповідає позитивному напрямку осі за правилом правого гвинта.
Координати вектора, отриманого поворотом вихідного щодо осі х
, виходять у результаті дії на нього матриці повороту:
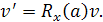 (1.15) (1.15)
Поворот вектора навколо довільної осі, що проходить через точку початку координат, можна звести до цих трьох типів повороту. Зміна координат вектора при поворотах системи координат щодо її осей описується матрицями, зворотними матрицям Rx
, Ry
, Rz
.
Довільна вісь обертання задається координатами:
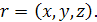 (1.16) (1.16)
Вона утворює із віссю z кут φ
, а її проекція на площину х0у
утворює із віссю х
кут θ (Рис. 1.4).
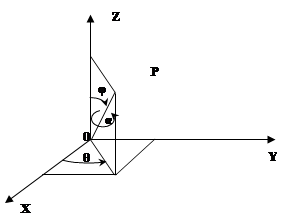
Рис. 1.4. Поворот навколо довільної осі обертання
Поворот навколо довільного вектора можна описати матрицею повороту:
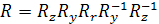 , (1.17) , (1.17)
де
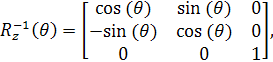 (1.18) (1.18)
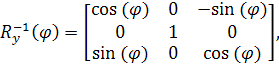 (1.19) (1.19)
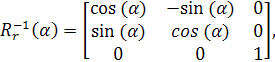 (1.20) (1.20)
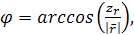 (1.21) (1.21)
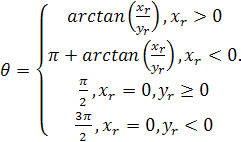 (1.22) (1.22)
Перетворення зрушення можна записати у формі матричного множення, якщо додати в запис вектора четвертий компонент, який дорівнює одиниці (такі координати називаються однорідними)
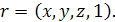 (1.23) (1.23)
і перейти до матриць 4x4:
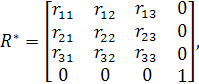 (1.24) (1.24)
Матриця зрушення буде мати наступний вигляд:
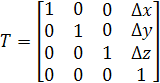 . (1.25) . (1.25)
Перетворення загального виду, тобто сполучення повороту зі зрушенням, може бути представлене у вигляді матриці:
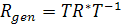 .(1.26) .(1.26)
При використанні однорідних координат матриця перетворення масштабування виглядає так:
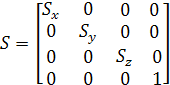 (1.27) (1.27)
1.2 Використання проекцій
При побудові реалістичних об’ємних зображенні варто враховувати ефект перспективи,
що полягає в тому, що паралельні лінії, що віддаляються від спостерігача, на відстані здаються людині збіжними.
З спостерігачем пов’язана точка спостереження
й напрямок спостереження.
Ефект перспективи обернено-пропорційний відстані від об’єкта до точки спостереження. Якщо око розташоване далеко від об’єкту, то паралельні лінії про об’єкта будуть здаватися паралельними й спостерігачеві. Якщо приблизитися до об’єкта на досить близьку відстань, ефект перспективи підсилиться
Положення об’єкта задається в системі світових координат.
При побудові зображення тривимірного об’єкта світові координати його точок треба перетворювати у двовимірні екранні координати. Проектування –
це перехід від світових координат до екранних [25].
Перехід відбувається у два етапи. Є система видових координат,
пов’язана зі спостерігачем. Світові координати перетворяться у видові за допомогою видового перетворення,
потім видові координати перетворюються в екранні. Це – перспективне перетворення.
Тип проектування на плоску, а не викривлену поверхню, де як в якості проекторів використаються прямі. а не скривлені лінії, називається плоскою геометричною проекцією. Плоскі геометричні проекції діляться на два види: центральні й паралельні. Якщо центр проекції перебуває на визначеній відстані від проекційної площини, то проекція - центральна. Якщо ж центр проекції віддалений на нескінченність, то проекція - паралельна.
Точкою сходження називається точка перетинання центральних проекцій будь-якої сукупності паралельний прямих, які не паралельні проекційної площини. Існує нескінченна множина точок сходження. Точка сходження називається головної, якщо сукупність прямих паралельна одній з координатних осей. Залежно від того, скільки координатних осей перетинає проекційну площину розрізняють одно-, двох- і трьохточкові проекції.
Прямокутні координати точки спостереження у світовій системі координат зв’язані зі сферичними координатами (ρ, φ, θ
) наступними співвідношеннями:
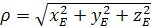 ,(1.28) ,(1.28)
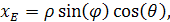 (1.29) (1.29)
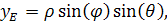 (1.30) (1.30)
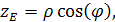 (1.31) (1.31)
Перетворення координат точки з світової системи координат у видову виконується за допомогою перетворення:
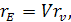 (1.32) (1.32)
де V
- матриця перетворення
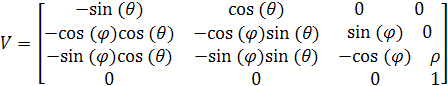 (1.33) (1.33)
У паралельних
проекціях ігнорується видиме порушення пропорцій, що виникає внаслідок різної віддалі об’єкта та його частин до спостерігача. Це відповідає віддаленню точки спостереження на нескінченну відстань. При цьому паралельні геометричні лінії об’єкта залишаються паралельними й після проектування В перспективних
проекціях ефект перспективи враховується [26].
Різновидність паралельної проекції – ортогональна
проекція – отримуються ігноруванням z
-координати після переходу у видову систему координат.
В ізометричній
проекції осі х, у
и z світової системи координат складають рівні кути із площиною екрана. Матриця ізометричної проекції має вигляд:
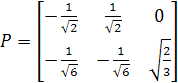 (1.34) (1.34)
У диметричній
проекції, що також відноситься до числа ортогональних, вісь z
проектується на вісь v
екранної системи координат, а проекції осей x
і y
складають заданий кут а
з негативною й позитивною півосями осі u
. Диметрична проекція включає ізометричну як частковий випадок [17].
У косокутній проекції осі y
i z
світової системи координат співпадають з осями u
i v
екранної системи, а проекція осі х
становить заданий кут а
з негативною півосю v
.
1.3 Алгоритми видалення невидимих ребер та граней
При побудові непрозорих об’єктів варто враховувати, що деякі ділянки їхньої поверхні не видні спостерігачеві, тому що закриваються іншими частинами об’єкта.
Є різні алгоритми видалення невидимих частин. Деякі із них засновані на сортуванні граней по відстані від спостерігача. Нехай є дві грані, що перебувають на різній відстані від точки спостереження (Рис. 1.5).

Рис. 1.5. Розташування закритих граней об’єкта щодо спостерігача
У цьому випадку друга грань закривається першою й вся вона або її частина стають невидимими. Першою на екран виводиться найбільш віддалена грань, останньої - найближча.
Алгоритми видалення невидимих граней можуть бути умовно поділені на два класи залежно від принципів, закладених для їхньої реалізації. Перший клас – це алгоритми що працюють в просторі об’єкта. Це означає, що для визначення видимості даної грані рівняється її взаємне розташування з усіма іншими гранями в тривимірній сцені. Нехай N
– кількість граней у тривимірній сцені. Для побудови тривимірної сцени в цьому випадку необхідно зрівняти положення кожної грані із тими, що залишилися, це вимагає порядку 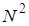 операцій. Наприклад, нехай кількість граней у тривимірній сцені операцій. Наприклад, нехай кількість граней у тривимірній сцені 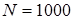 , тоді час роботи алгоритмів цього класу порядку 1 000 000 операцій [11]. , тоді час роботи алгоритмів цього класу порядку 1 000 000 операцій [11].
Другий клас алгоритмів - працюючих у просторі зображення, заснований на знаходженні точки найближчої грані яку перетинає промінь зору, що проходить через задану точку на екрані. Оскільки число точок на растровому екрані фіксоване, то алгоритми цього класу менш чутливі до збільшення кількості об’єктів у тривимірній сцені. Нехай n
- число точок на растровому екрані. Тоді кількість операцій, необхідних для побудови тривимірної сцени буде порядку 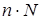 . Наприклад, для екранного розширення 320 . Наприклад, для екранного розширення 320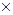 200 точок, 200 точок, 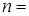 64000, тоді кількість операцій для 64000, тоді кількість операцій для 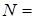 1000 граней буде порядку 64 000 000. Вибір класу алгоритму може залежати від особливостей конкретної задачі, а також від способів реалізації алгоритму. 1000 граней буде порядку 64 000 000. Вибір класу алгоритму може залежати від особливостей конкретної задачі, а також від способів реалізації алгоритму.
Один з методів сортування полягає в наступному. Нехай задані координати вершин першої грані 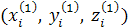 і другої грані і другої грані 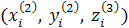 .Обчислюються координати середніх точок граней: .Обчислюються координати середніх точок граней:
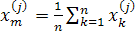 , (1.35) , (1.35)
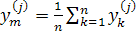 , (1.36) , (1.36)
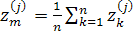 , (1.37) , (1.37)
де п -
кількість вершин кожної грані. При виконанні геометричних перетворенні об’єкта, наприклад при його поворотах, перетворюються й координати середніх точок граней. Будемо вважати, що напрямок спостереження — уздовж осі х.
Перед побудовою об’єкта проводимо сортування середніх точок його граней по х
-координаті й малювання граней починається з найбільш віддаленої. Цей метод називається алгоритмом художника.
Розглянутий алгоритм не дуже ефективний, оскільки припускає вивід навіть тих частин об’єкта, які спостерігачеві не видні. Є й інші алгоритми видалення невидимих частин об’єкта. Серед них алгоритм z
-буфера й деякі інші.
Z
-буфер являє собою "поточкову" копію екрана, яку можна зберігати, наприклад, у виді масиву цілих значень. Спочатку всім елементам цього масиву привласнюються початкові значення, рівні максимально припустимим цілим. Кожній точці зображення поверхні зіставляється значення відстані від цієї точки до площини спостереження. При виводі зображення чергової точки поверхні це значення параметра рівняється зі значенням, записаним для неї в z
-буфері. Якщо при цьому виявляється, що значення з z
-буфера більше, графічна крапка виводиться на екран, тому що вона перебуває ближче до спостерігача. Відстань до точки заноситься в z
-буфер. У протилежному випадку графічна точка не виводиться, оскільки вона "затуляється" уже намальованою точкою. Описаний алгоритм виявляється більш ефективним при побудові складних поверхонь, хоча і вимагає додатковий затрат пам’яті.
Ще один метод визначення невидимих поверхонь заснований на використанні нормалі –
перпендикуляра до поверхні грані. Якщо вважати, що нормаль спрямована з об’єкта назовні, то у видовій системі координат проекція нормалі па вісь z,
яку ми вважаємо що вона іде до площини екрану і спостерігача, буде позитивною, у тому випадку, коли грань видна спостерігачеві, і негативної, коли не видна. Як побудувати нормаль? Якщо вважати, що дві сторони багатокутника, що виходять із загальної вершини, є векторами, то їхній векторний добуток можна прийняти за нормаль до поверхні цього багатокутника. Напрямок нормалі буде однозначно визначено, якщо задано порядок векторних співмножників. Спрощений варіант даного алгоритму укладається в те, що вершини грані нумеруються по годинниковій стрілці. Якщо подивитися на цю грань із "тильної" сторони, нумерація вершин буде йти проти годинникової стрілки. Порядок нумерації, таким чином, можна використати для визначення того, чи видна дана грань із обраної точки спостереження [12].
Крім універсальних алгоритмів, існує ряд вузькоспеціалізованих. Так існує алгоритм видалення невидимих граней опуклих тіл, що дозволяє робити обчислення набагато швидше. Він працює для центральної перспективної проекції. Розглянемо роботу цього алгоритму на прикладі як зображене на Рис. 1.6.:
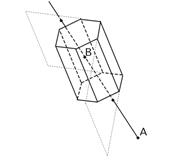
Рис. 1.6. Перетинання прямої AB
із площинами граней призми
Нехай спостерігач перебуває в точці A
. Виберемо точку B
, що свідомо є внутрішньою для опуклої фігури, в даному випадку призми. Виберемо деяку грань, про яку ми хочемо довідатися видима вона із точки A
, або не видима. Побудуємо площину, у якій лежить обрана грань. Знайдемо точку перетину площини й прямої, що утворена відрізком AB
. Якщо точка перетину прямої і площини лежить всередині відрізка AB
, то робимо висновок, що дана грань видима. Якщо точка перетину перебуває поза відрізком AB
, то грань є не видима. У випадку, коли пряма й площина паралельні, вважаємо що грань не видима.
1.4 Методи програмування динамічних зображень
Анімацією
називають вивід що змінюється, динамічного зображення. Ілюзію зображення, що рухається, створює перегляд послідовності нерухомих зображеннь-кадрів, що показують різні фази руху. Щоб вивести на екран дисплея динамічне зображення, треба запрограмувати вивід послідовності кадрів. Швидкість зміни кадрів при цьому повинна бути досить великою. Якщо кожний кадр містить складне зображення, що складається з великої кількості графічних елементів, вирішити проблему швидкого виведення кадрів на екран непросто.
Найпростіший метод анімації - перемальовування графічного екрана. Незважаючи на простоту зображень, очевидним виявляється мерехтіння зображення і його "посмикування" при перемальовуванні, Так можна використати такий метод, що виводить поверхню задавши рівняння:
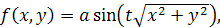 (1.38) (1.38)
де а –
амплітуда, a t
– параметр, що грає роль часу. Анімація використається для виведення тимчасової залежності графіка функції. Оскільки мова йде про вивід тривимірного об’єкта, необхідно вибрати проекцію, наприклад симетричну поверхня зображується лініями її перетинання із площинами, паралельними площинам х0z
і у0z.
Через певний час попереднє зображення "затирається" чорними кольорами. При цьому спостерігається неприємне мерехтіння екрана.
Позбутися від зазначеного недоліку можна, використовуючи сторінки відеопам’яті.
Організація відеопам’яті така, що в деяких режимах роботи відеоадаптера є кілька сторінок відеопам’яті. На екрані дисплея відображається тільки одна з них, а всі інші можуть бути в цей час використані для побудови чергового кадру анімаційного зображення [17].
Подальша оптимізація може бути досягнута за рахунок більш акуратного програмування основних графічних процедур. Для цього, як правило, доводиться вставляти у вихідний текст програми фрагменти коду мовою асемблера [3].
Є й інші проблеми, які доводиться вирішувати при програмуванні динамічних зображень. Так, наприклад, переміщення об’єкта може відбуватися на тлі нерухомого зображення. При цьому необхідно тимчасово зберігати невидимі ділянки тла й відновлювати його після того, як об’єкт зміститься в нове положення. Одне з рішень даної проблеми полягає у використанні спрайтів –
апаратних або програмних засобів формування динамічного зображення. Спрайт являє собою растрове зображення невеликого розміру, що може переміщатися по екрані незалежно від іншої "картинки". Спрайт накладається на основне зображення, перекриваючи його [15].
На сьогоднішній час для програмування 3d-анімації використовуються спеціалізовані програмні засоби, які в більшій мірі використовують можливості сучасних відеокарт, які самі проводять необхідні обрахунки вершин, обробляють зображення і виводять його на екран. Швидкість обрахунку необхідних операцій настільки велика, що практично є моментальною, швидкість зміни зображення на екрані відбувається швидше, ніж встигає це помітити людське око [15].
РОЗДІЛ ІІ
. ПРАКТИЧНА РЕАЛІЗАЦІЯ 3D ОБ’ЄКТІВ
ТА ДИНАМІЧНИХ ПОДІЙ
2.1 Модуль обробки 3d об’єктів
Для відображення можливостей роботи із об’ємними фігурами нами було створено відповідний модуль, що дає змогу:
- перетворювати 3d координати в 2d координати монітора;
- вибирати відповідну проекцію за бажанням користувача;
- повертати точку відносно центру координат;
- повертати точку відносно певного вектору;
- відображати на екрані лінію, точку задану відповідними просторовими координатами;
- проводити масштабування точок відносно початку координат;
- рухати точку у довільному напрямку.
Розглянемо більш детально даний модуль:
Перш за все, в ньому оголошено глобальні зміні, які відповідатимуть за координати точки в просторі, на екрані:
type vector=array[1..3] of Real;
projection=array[1..2] of vector;
type Toch2d=record
x,y:integer;
end;
type Toch3d=record
x,y,z:real;
end;
var
abs_x_center, abs_y_center: Integer;DriverP: Pointer;
Даний модуль містить ряд функцій, а саме, функції Procedure open_graph
та Procedure close_graph
відповідають за ініціалізацію та вихід із графічного режиму.
Процедура Procedure out_text_XY(ss: String; x,y:integer; color: Word)
відповідає за відображення текстового рядка заданим кольором за відповідними координатами.
Процедура Procedure put_picxel(d2:Toch2d; color: Word)
за координатами точки у двохвимірному просторі за заданим кольором відображає її на екран.
Процедура Procedure norm_line(d2_0,d2_1:Toch2d; color:word)
за координатами 2 точок у двохвимірному просторі за заданим кольором будує на екран лінію.
Дані процедури побудовані на основі стандартних функцій.
Відповідно до формул 1.33 та 1.34 вибору проекцій відображення побудовані матриці перетворення в ізометричній, диметричній та ортогональній проекції. Дані матриці необхідні для переходу від 3d до 2d координат:
Procedure computer_isometric_matrix(var P:projection);
Begin
P[1,1]:=-1.0/Sqrt(2.0);
P[1,2]:=-P[1,1];
P[1,3]:=0.0;
P[2,1]:=-1.0/Sqrt(6.0);
P[2,2]:=P[2,1];
P[2,3]:=-2.0*P[2,1];
End;
Procedure computer_dimetric_matrix(alpha: Real; var P: projection);
Var
t: Real;
Begin
alpha:=pi*alpha/180.0;
P[1,1]:=-1.0/Sqrt(2.0);
P[1,2]:=-P[1,1];
P[1,3]:=0.0;
t:=Sin(alpha)/cos(alpha);
P[2,1]:=t*P[1,1];
P[2,2]:=P[2,1];
P[2,3]:=Sqrt(1.0-Sqr(t));
End;
Procedure computer_oblique_matrix(alpha: Real; var P: projection);
Begin
alpha:=pi*alpha/180.0;
P[1,1]:=-Sin(alpha);
P[1,2]:=1.0;
P[1,3]:=0.0;
P[2,1]:=-Cos(alpha);
P[2,2]:=0.0;
P[2,3]:=1.0;
End;
Процедура повороту точки відносно початку координат побудована у відповідності до формул 1.12 – 1.22 і має вигляд:
Procedure povorot(var mas:Toch3d; kx,ky,kz:real);
var tx,ty,tz,y,x,z:real;
Begin
tx:=mas.x;
ty:=mas.y*cos(kx*pi/180)+mas.z*sin(kx*pi/180);
tz:=mas.y*(-sin(kx*pi/180))+mas.z*cos(kx*pi/180);
y:=ty;
x:=tx*cos(ky*pi/180)+tz*(-sin(ky*pi/180));
z:=tx*sin(ky*pi/180)+tz*cos(ky*pi/180);
mas.z:=z;
mas.x:=x*cos(kz*pi/180)+y*sin(kz*pi/180);
mas.y:=-x*sin(kz*pi/180)+y*cos(kz*pi/180);
End;
У відповідності до формули 1.25 побудована процедура руху точки:
Procedure rux(var mas:Toch3d; dx,dy,dz:real);
Begin
mas.x:=mas.x+dx;
mas.y:=mas.y+dy;
mas.z:=mas.z+dz;
End;
У відповідності до формули 1.27 побудована процедура масштабування:
Procedure mach(var mas:Toch3d; mx,my,mz:real);
Begin
mas.x:=mas.x*mx;
mas.y:=mas.y*my;
mas.z:=mas.z*mz;
End;
Для переходу з трьохмірої моделі до двомірної використовується процедура project(const P:projection; const d3:Toch3d; const c:Toch2d; var d2:Toch2d)
, що за заданими координатами 3d точки та вибраною матрицею проекції проводить перевід у двовимірні координати монітору:
Procedure project(const P:projection; const d3:Toch3d; const c:Toch2d; var d2:Toch2d);
Begin
d2.x:=c.x+Round(P[1,1]*d3.x+P[1,2]*d3.y+P[1,3]*d3.z);
d2.y:=c.y+Round(P[2,1]*d3.x+P[2,2]*d3.y+P[2,3]*d3.z);
End;
Даного модуля в принципі достатньо для реалізації побудови 3d об’єктів, анімації. Адже більшість операцій відбувається саме із вершинами об’єкта, а даний модуль саме їх і описує.
2.
2 Відображення об’ємних фігур в різних проекціях
Для розуміння вигляду фігур у різних проекціях побудовано каркас тетраедра із виведенням його у диметричній, ізометричній та ортогональній проекціях.
Тетраедр задається чотирма своїми вершинами і почергово виводиться на екран.
Всі вершини зображення тетраедра з’єднуються лініями. Щоб вивести зображення тетраедра в заданій проекції, необхідно обрахувати значення екранних координат і провести відрізки прямих. Зображення тетраедра виводиться в ізометричній, косокутній і диметричній проекціях, причому спочатку виводиться статичне зображення, а вже потім воно перемальовується в циклі по куту проектування:
d3:array[1..4] of Toch3d;
c:Toch2d;
d2:array[1..4] of Toch2d;
xstep,ystep,theta: Real;
i,j,xold,yold,xnew,ynew: Integer;
p:projection;
…
abs_x_center:= 0;
abs_y_center:= 0;
d3[1].x:=0;d3[1].y:=0;d3[1].z:=0;
d3[2].x:=0;d3[2].y:=0;d3[2].z:=50;
d3[3].x:=0;d3[3].y:=50;d3[3].z:=0;
d3[4].x:=50;d3[4].y:=0;d3[4].z:=0;
….
out_text_XY('Oblique Projection', -150, 150, Yellow);
draw_tetra;
Readln;
theta:=45;
repeat
computer_oblique_matrix(theta, P);
ClearViewPort;
draw_tetra;
theta:=theta+1;
until KeyPressed;
Дана програма дає можливість візуально побачити різницю між різними проекціями і вибрати оптимальну для користувача.
2.3 Побудова поверхонь
Для побудови поверхні була використана формула 1.38 і показана можливість її виведення 2 способами, стандартними засобами та із використанням сторінки відеопам’яті.
function f(x,y: Real): Real;
begin
f:=20*Sin(t*Sqrt(x*x+y*y));
end;
procedure anim(tt: Byte);
begin
ux:=Abs(b-a)/(nx-1);
uy:=Abs(d-c)/(ny-1);
d3.x:=a; d3.y:=c; d3.z:=f(d3.x,d3.y);
project(P,d3,cc,d2[1,1]);
d2[1,1].x:=d2[1,1].x+GetMaxX div 2;
d2[1,1].y:=GetMaxy div 2 - d2[1,1].y;
xmin:=d2[1,1].x; xmax:=xmin;
ymin:=d2[1,1].y; ymax:=ymin;
for i:=1 to nx do
begin
d3.y:=c;
for j:=1 to ny do
begin
d3.z:=f(d3.x,d3.y);
project(P,d3,cc,d2[i,j]);
d2[i,j].x:=d2[i,j].x+GetMaxX div 2;
d2[i,j].y:=GetMaxY div 2 - d2[i,j].y;
if xmin>d2[i,j].x then xmin:=d2[i,j].x
else if xmax<d2[i,j].x then xmax:=d2[i,j].y;
if ymin>d2[i,j].y then ymin:=d2[i,j].y
else if ymax<d2[i,j].y then ymax:=d2[i,j].y;
d3.y:=d3.y+uy;
end;
d3.x:=d3.x+ux;
end;
SetColor(tt);
for i:=1 to nx do
begin
MoveTo(d2[i,1].x,d2[i,1].y);
for j:=2 to ny do LineTo(d2[i,j].x,d2[i,j].y);
end;
for j:=1 to ny do
begin
MoveTo(d2[1,j].x,d2[1,j].y);
for j:=1 to nx do LineTo(d2[i,j].y,d2[i,j].x);
end;
end;
Begin
open_graph;
t:= 0;
theta:= 20;
repeat
computer_dimetric_matrix(theta, P);
anim(12);
anim(0);
t:=t+0.0001;
delay(10000);
until KeyPressed;
Відмінність у побудові поверхні із використанням відеопам’яті полягає в тому, що немає необхідності перемальовувати зображення щоразу, а просто зміннюючи відеосторінку, очищаємо її на активній малюємо малюнок і робимо її видимою:
SetGraphMode(VGAMed);
k:=1;
t:= 0;
theta:= 20;
repeat
computer_dimetric_matrix(theta, P);
k:=1-k;
SetActivePage(k);
ClearDevice;
anim(12);
SetActivePage(k);
t:=t+0.001;
until Keypressed;
2.4 Відсікання невидимих ліній, використання модуля Graph3d
Нижче, у відповідності до формул 1.35 – 1.37 реалізовано алгоритм відсікання невидимих частин алгоритмом сортування граней. Для цього використали побудову тетраедра. Перш ніж вивести на екран грань проводимо обрахунок чи є вона видима чи ні, і в залежності від результату проводимо прорисовку.
procedure draw_poly(j, color: Word);
var
vertex: array[1..3] of PointType;
i,k:Word;
begin
i:=1;
k:=1;
repeat
if i<>j then
begin
project(P,d3[i], c, d2[k]);
inc(k);
end;
Inc(i);
until k=4;
SetFillStyle(SolidFill, color);
FillPoly(3, d2);
end;
Для повного відображення можливостей модуля Graph3d було реалізовано ряд програм, зокрема: Surf3.pas – відображення рухомої поверхні подібної до розходження хвиль від джерела удару; Solar.pas – імітація руху планет навколо сонця, використовує диметричну проекцію та працює з використанням відеосторінок; MY_3D.pas – забезпечує реалізацію основних елементів перетворення у просторі а саме, клавіші відповідають:
- PgUp – поворот точок за годинниковою стрілкою навколо осі Z;
- PgDn – поворот точок проти годинникової стрілки навколо осі Z;
- Home– поворот точок за годинниковою стрілкою навколо осі X;
- End – поворот точок проти годинникової стрілки навколо осі X;
- Insert– поворот точок за годинниковою стрілкою навколо осі Y;
- Delete – поворот точок проти годинникової стрілки навколо осі Y;
- "Q" – рух по осі Z в додатному напрямку;
- "E" – рух по осі Z в протилежному напрямку;
- "W" – рух по осі Y в додатному напрямку;
- "S" – рух по осі Y в протилежному напрямку;
- "A" – рух по осі X в додатному напрямку;
- "D" – рух по осі X в протилежному напрямку;
- "+" – збільшити масштаб;
- "-" – зменшити масштаб.
Дана програма використовує диметричну проекцію побудови зображень та не використовує роботи з відеопам’яттю.
ВИСНОВКИ
Проаналізувавши проблему використання комп’ютерної графіки, зокрема об’ємних фігур, ролі анімації та методів її відображення і у відповідності до мети курсової роботи було виконано наступне:
1. проведено детальний аналіз літератури та Інтернет-джерел за темою "Тривимірна графіка. Анімація";2. виокремлення основних понять, формул і методів роботи із об’єктами у тривимірному просторі;3. проведено детальний аналіз розділу математики "Вектори, матриці", де було виокремлено основні поняття по роботі з векторами, матрицями, які спрощують розуміння учнями основних подій в 3d просторі;4. практично реалізовано основні алгоритми роботи по діям над точкою в просторі:
- рух;
- поворот;
- масштабування;
5. сформовано лекційний теоретичний матеріали.
Результатом роботи є лекційний курс по програмування тримірної графіки та методика відображення анімаційних проектів з допомогою стандартних засобів мови програмування Pascal, без використання сторонніх бібліотек. Даний лекційний курс побудований лише на математичних функціях і їх використанні на мові програмування. Він охоплює такі області як векторна, матрична математика. Даний курс доповнений реалізованими прикладами, що дають практичне уявлення про застосування математичних моделей у програмуванні, вчать аналітично реалізовувати поставленні завдання, покладаючись на різноманітні алгоритми та методи.Кінцевий продукт має практичну цінність у застосуванні при роботі із поєднання програмування із математикою, даючи наглядне розуміння взаємодії і використання математичних методів та фунцій, їх застосування на практиці.
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
1. Turbo Pascal – Издательская група К.: ВНV, 2000. – 320 с.
2. Абрамов В. Г. Введение в язык Pascal: Учебное пособие для студентов вузов по специальности Прикладная математика. – М.: Наука, 1988. – 158 с.
3. Абрамов С. А. Начала программирования на языке Pascal. - М.: Наука, 1987. – 126 с.
4. Аммерал А. Машинная графика на языке С, в 4-х томах, изд-во Сол. Систем, – 1992. – 230 с.
5. Власик А.П. Практикум з програмування в середовищі Turbo Pascal. – Рівне. – НУВГ,- 53 с.
6. Вэн-Дэм. А. Основы интерактивной машинной графики, т.1-2, М. Мир, 1985. – 257 с.
7. Гилой. Интерактивная машинная графика. – М., Мир, –1981. – 210 с.
8. Грайс. Графические средства персональных компьютеров. – М., – Мир, 1980. – 142 с.
9. Грис Д. Наука программирования. M.: Мир, 1984. – 230 с.
10. Джонс Ж., Харроу К. Решение задач в системе Турбо Паскаль. М, 1991. – 709 с.
11. Жикин А.Е. Компьютерная графика. Динамика, реалистические ихображения, М., Диалог-МИФИ, – 1995 – 324 с.
12. Зуев Е. А. Язык программирования Турбо Паскаль 6.0, 7.0. – М.: Радио и связь, 1993. – 150 с.
13. Ковалюк Т.В. Основи програмування. Київ: Видавнича група ВНV, 2005. – 385 с.
14. Культин Н. Б. Программирование в TurboPascal 7.0 и Delphi. - Санкт- петербург,1999. – 120 с.
15. Майкл Ласло. Вычислительная геометрия и компьютерная графика на С++. Москва – Бином, 1997. – 440 с.
16. Марченко А.И., Марченко Л.А. Программирование в среде Turbo Pascal 7.0. К.: ВЕК, – 2000. – 441 с.
17. Немнюгин С.А. TurboPascal Практикум. 2-е издание. – С-Пб., – Питер– 2003, - 267 с.
18. Перминов О. Н. Программирование на языке Паскаль. – М.: Радио и связь, – 1988. – 97 с.
19. Перминов О. Н. Язык программирования Pascal. – М.: Радио и связь,– 1989. – 205 с.
20. Препарата Ф. Вычислительная геометрия: Введение, М. Мир, 1989. ч.1.- Рівне: НУВГП, 2005. – 179 с.
21. Роджерс, Адамс, Математические основы машинной графики, – М.? Машиностроение, – 1985.– 102 c.
22. Роджерс С.А. алгоритмические основы машинной графики. М. Мир, 1989. – 235 с.
23. Тихомиров Ю. Программирование трехмерной графики, С.-Пб.: БХВ‑Санкт-Петербург,1999. – 350 с.
24. Томпсон Н. Секреты программирования трехмерной графики для Windows 95. Перев с англ. – СПб: Питер, – 1997. – 352 с.
25. Фокс А. Вычислительная геометрия, М., Мир, – 1982. – 421 с.
26. Хонич А. Как самому создать трехмерную игру. М.:МИКРОАРТ, 1996. – 220 с.
|