ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
КАМСКАЯ ГОСУДАРСТВЕННАЯ ИНЖЕНЕРНО-ЭКОНОМИЧЕСАЯ АКАДЕМИЯ
КАФЕДРА «ЭКОНОМИКА, ОРГАНИЗАЦИЯ И УПРАВЛЕНИЕ ПРОИЗВОДСТВОМ»
КОНТРОЛЬНАЯ РАБОТА
ПО ДИСЦИПЛИНЕ «МАТЕМАТИЧЕСКИЕ МЕТОДЫ И МОДЕЛИ В ЭКОНОМИКЕ»
Вариант № 7
Набережные Челны
2010 г
Задача № 1
Бригада приняла заказ на изготовление 55 шт. продукции П1, 63 шт. продукции П2 и 75 шт. продукции П3. Продукция производится на станках А и В. Для изготовления на станке А единицы продукции П1 требуется 14 мин., единицы продукции П2 - 47 мин., единицы продукции П3 - 21 мин., на станке В - соответственно 16, 18 и 12 мин.
Постройте ММ задачи, на основании которой можно найти сколько продукции и какого вида следует изготовить на станках А и В, чтобы заказ был выполнен в минимальное время.
РЕШЕНИЕ:
Искомыми величинами в задаче являются объемы выпуска изделий. Изделия будут выпускаться двумя станками А и В. Поэтому необходимо различать количество изделий П1, произведенных станками А и В. Аналогично, объемы выпуска изделий П2 и П3, произведенных станками А и В также являются различными величинами. Вследствие этого в данной задаче 6 переменных. Для удобства восприятия будем использовать двухиндексную форму записи: xji
– количество изделий Пj (j=1,2,3), изготавливаемых на станках А (i=1) и В (i=2), а именно,
x11
– количество изделий П1, изготавливаемых на станке А , [шт.];
x12
– количество изделий П1, изготавливаемых на станке В , [шт.];
x21
– количество изделий П2, изготавливаемых на станке А, [шт.];
x22
– количество изделий П2, изготавливаемых на станке В , [шт.];
x31
– количество изделий П3, изготавливаемых на станке А, [шт.];
x32
– количество изделий П3, изготавливаемых на станке В, [шт.].
Представим исходные данные задачи в таблице:
| Время, мин/шт |
| П1 |
П2 |
П3 |
| А |
14 |
47 |
21 |
| В |
16 |
18 |
12 |
| заказ, шт |
55 |
63 |
75 |
Целевая функция
Целью решения задачи является выполнение заказа с минимальными затратами времени, т.е. критерием эффективности решения служит показатель времени на выполнение всего заказа. Поэтому ЦФ должна быть представлена формулой расчета затрат времени. Затраты времени станками на производство одного изделия известны из условия. Таким образом, ЦФ имеет вид:
Реклама

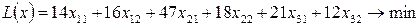 , ,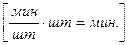
Ограничения
Возможные объемы производства продукций станками ограничиваются следующими условиями:
· общее количество продукции П1, выпущенное обеими станками, должно равняться 55 шт., продукции П2 - 63 шт., продукции П3 – 75 шт;
· объемы производства изделий не могут быть отрицательными величинами.
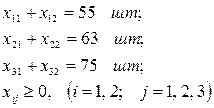
Таким образом, математическая модель этой задачи имеет вид:
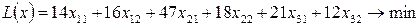 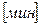 , ,

ЗАДАЧА № 2
Решить одноиндексную задачу линейного программирования графическим методом.

РЕШЕНИЕ:
1) Построим следующие прямые (см.рис.2.1)
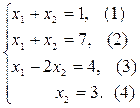
Для этого вычислим координаты точек пересечения этих прямых с осями координат
(1) - 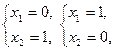 (2); - (2); - 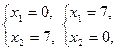 (3) - (3) - 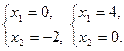
(2),(3) После проведения штриховки допустимых полуплоскостей определяем, что ОДР - это многоугольник ABCDEF.
(4) Целевую прямую можно построить по уравнению
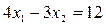 , , 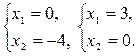
(5) Построим вектор 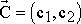 , который начинается в точке (0;0), заканчивается в точке , который начинается в точке (0;0), заканчивается в точке 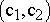 , то есть , то есть 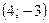 . Если целевая прямая и вектор . Если целевая прямая и вектор 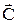 построены верно, то они будут перпендикулярны. построены верно, то они будут перпендикулярны.
 Рисунок 2. 1. Рисунок 2. 1.
(6) Точка Е - это последняя вершина многоугольника допустимых решений, через которую проходит целевая прямая, двигаясь по направлению вектора 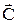 , т.е. т.Е - это точка максимума ЦФ. , т.е. т.Е - это точка максимума ЦФ.
(7) Координаты точки Е, найдем как решение системы уравнений
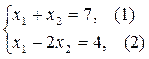
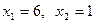 , ,
т. max 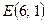 [т]. [т].
(8) Таким образом, максимальное значение ЦФ равно
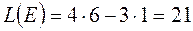 [руб.]. [руб.].
ЗАДАЧА № 4
Завод радиоэлектронной аппаратуры производит 880 радиоприемников в сутки. Микросхемы для радиоприемников (по 1 шт. на приемник) производятся на этом же заводе с интенсивностью 3800 тыс. шт. в сутки. Затраты на подготовку производства партии микросхем составляют 74 руб. (числа в задаче условные)
, себестоимость производства 1 тыс. шт. микросхем равна 24 руб. Хранение микросхем на складе обходится заводу в 1,7 руб. за каждую тысячу в сутки. У завода появилась возможность закупать микросхемы в другом месте по цене 28 руб. за 1 тыс. шт. Стоимость доставки равна 31 руб.
Выясните, стоит ли заводу закупать микросхемы вместо того, чтобы их производить. Для более выгодного режима работы завода (производство или закупка) определите периодичность подачи заказа, и затраты на управление запасами в месяц (22 рабочих дня).
Решение:
Математические модели управления запасами (УЗ) позволяют найти оптимальный уровень запасов некоторого товара, минимизирующий суммарные затраты на покупку, оформление и доставку заказа, хранение товара, а также убытки от его дефицита. Модель Уилсона является простейшей моделью УЗ и описывает ситуацию закупки продукции у внешнего поставщика, которая характеризуется следующими допущениями:
Реклама

· интенсивность потребления является априорно известной и постоянной величиной;
· заказ доставляется со склада, на котором хранится ранее произведенный товар;
· время поставки заказа является известной и постоянной величиной;
· каждый заказ поставляется в виде одной партии;
· затраты на осуществление заказа не зависят от размера заказа;
· затраты на хранение запаса пропорциональны его размеру;
· отсутствие запаса (дефицит) является недопустимым.
Модель планирования экономичного размера партии
Модель Уилсона, используемую для моделирования процессов закупки продукции у внешнего поставщика, можно модифицировать и применять в случае собственного производства продукции. На рис. схематично представлен некоторый производственный процесс. На первом станке производится партия деталей с интенсивностью 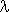 деталей в единицу времени, которые используются на втором станке с интенсивностью деталей в единицу времени, которые используются на втором станке с интенсивностью  [дет./ед.t]. [дет./ед.t].

Входные параметры модели планирования экономичного размера партии
1) 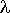 – интенсивность производства продукции первым станком, [ед.тов./ед.t]; – интенсивность производства продукции первым станком, [ед.тов./ед.t];
2)  – интенсивность потребления запаса, [ед.тов./ед.t]; – интенсивность потребления запаса, [ед.тов./ед.t];
3) s – затраты на хранение запаса, [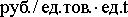 ]; ];
4) K – затраты на осуществление заказа, включающие подготовку (переналадку) первого станка для производства продукции, потребляемой на втором станке, [руб.];
5) 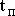 – время подготовки производства (переналадки), [ед.t]. – время подготовки производства (переналадки), [ед.t].
Выходные параметры модели планирования экономичного размера партии
1) Q – размер заказа, [ед.тов.];
2) L – общие затраты на управление запасами в единицу времени, [руб./ед.t];
3)  – период запуска в производство партии заказа, т.е. время между включениями в работу первого станка, [ед.t]; – период запуска в производство партии заказа, т.е. время между включениями в работу первого станка, [ед.t];
4) 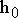 – точка заказа, т.е.размер запаса, при котором надо подавать заказ на производство очередной партии, [ед.тов.]. – точка заказа, т.е.размер запаса, при котором надо подавать заказ на производство очередной партии, [ед.тов.].
Формулы модели Уилсона:
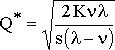 (формула Уилсона), (формула Уилсона),
где  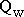 – оптимальный размер заказа в модели Уилсона; – оптимальный размер заказа в модели Уилсона;
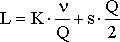 ; ;
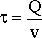 ; ;
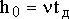 . .
Для данного завода выгодным режимом работы будет закупка микросхем, определим периодичность подачи заказа, и затраты на управление запасами в месяц.
Примем за единицу времени сутки.
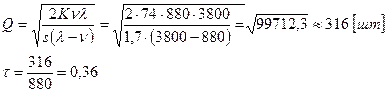
Подача каждого нового заказа должна производиться через 0,36 суток.
Поскольку надо определить периодичность за месяц (22 раб. дня):
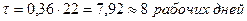
Годовые затраты на УЗ равны:
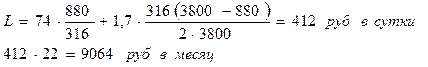

|