Государственное образовательное учреждение
высшего профессионального образования
ВОЛГО-ВЯТСКАЯ АКАДЕМИЯ ГОСУДАРСТВЕННОЙ СЛУЖБЫ
Дзержинский филиал
Кафедра «Математических и естественнонаучных дисциплин»
Курсовой проект
по дисциплине «Методологические основы информационного обеспечения управления»
Особенности метода кластерный анализ при большом количестве наблюдений (кластерный анализ метод К-средних) в социологических исследованиях
Специальность:
«Государственное и
муниципальное управление»
Оценка за курсовой проект ______________
_____________________
(подпись руководителя)
|
|
Выполнила:
студентка гр. 07 - ГОД - 1
Танаева А. В.
Научный руководитель:
КПН, доцент
Поляков Е. А.
|
Дзержинск
2011 г
.
РЕЦЕНЗИЯ
На курсовой проект
студента ____ курса, группа №_______
________________________________________________________________
(фамилия, имя, отчество)
Вопросы оценки:
Соответствие работы выбранной в соответствии с заданием теме_________________________________________________________________
(соответствует, не соответствует)1
- Обоснование актуальности работы 2
______________________________________
- Логичность общих выводов в заключении_________________________________
(актуальна, неактуальна)
4.Правильность выбора основной цели работы и соответствие задач, поставленных для достижения цели______________________________________________________
5 Научная новизна_______________________________________________________
6 Правильность проводимых расчетов (для проектов)_________________________
7 Самостоятельность в работе ____________________________________________
8 Правильность оформления работы в соответствии с методическими указаниями руководителя_______________________________________________________________
9 Своевременность представления работы руководителю: _____________________
(своевременно, с опозданием)
Логичность общих выводов в заключении_________________________________
Общая оценка за работу
- ___________________________________________________
Научный руководитель работы ________________________________________________
(ученая степень, звание, подпись, расшифровка подписи)
«___»______________200__г.
Примечания:
1. Оценка за работу выставляется в ведомость по пятибалльной системе как среднее арифметическое из суммы всех полученных оценок.
2. При получении неудовлетворительных оценок по пунктам 1 или 8, работа оценивается неудовлетворительно и возвращается на доработку.
3. При несвоевременной сдаче контрольной работы руководителю общая оценка снижается на 1 балл.
4. Работа должна быть представлена руководителю для рецензирования не позднее, чем за 10 дней до начала экзаменационной сессии.
Реклама

5. Студент, не выполнивший работу к экзамену (зачету) не допускается.
1
критерии оценки соответствия:
- не соответствует
– неудовлетворительно
- работа возвращается для устранения
недостатков – более 25% работы содержит материал, не имеющий к ней отношения (определяется от общего количества параграфов)
- соответствует -
т.е. менее 25% работы содержит материал, не имеющий к ней отношения (определяется от общего количества параграфов)
Данный пункт на суммарную оценку не влияет, если недостаток устранен студентом до сдачи работы в указанный срок.
2
при обосновании актуальности курсовой работы
оценка определяется по следующим критериям:
тема актуальна
– если студентом дана:
· правильная оценка проблемы с точки зрения современных взглядов на ее историческое значение;
· практическая и теоретическая значимость работы в настоящее время;
· возможность и необходимость дальнейшего совершенствования и развития основных положений рассматриваемой проблемы.
Оглавление
Введение
……………………………………………………………………………………………..4Глава 1. Кластерный анализ
……………………………………......5
1.1. Алгоритм кластерного анализа k-средних (k-means)……………………..5
1.1.1.Описание алгоритма
………………………………………………...6
1.1.2. Проверка качества кластеризации……………………………....7
1.2. АлгоритмPAM ( partitioning around Medoids)…………………………………8
1.3. Сложности, возникающие при кластерном анализе………………………..9
1.4. Сравнительный анализ иерархических и неиерархических методов кластеризации……………………………………………………………………………10
Глава 2. Алгоритмыкластерногоанализа…………….11
2.1. Алгоритм BIRCH (Balanced Iterative Reducing and Clustering using Hierarchies)…………………………………………………………………………………11
2.2.
Алгоритм
WaveCluster
…………………………………………………………11
2.3. Алгоритмыкластерного
анализа
Clarans, CURE, DBScan……………...12
2.4.
Алгоритм
CLARA (Clustering LARge Applications)………………………...12
2.5. Итеративная кластеризация в SPSS
……………………………………...13
2.6. Кластеризация в Data Mining…………………………………………………16
Глава 3. Опрос, посвященный психологическому состоянию личности
…………………………………………………….19
3.1. Факторный анализ
……………………………………………………………...19
3.2. Быстрый кластерный анализ
………………………………………………..21
Приложение
………………………………………………………………………24
1. Анкета, с помощью которой я смогу провести факторный анализ
…..24
2. Матрица, которая получилась после набивки анкеты
…………………...26
Заключение
……………………………………………………………………….27
Список используемых источников
………………………….28
Введение
Кластерный анализ
(англ. Dataclustering) — задача разбиения заданной выборки объектов (ситуаций) на подмножества, называемые кластерами, так, чтобы каждый кластер состоял из схожих объектов, а объекты разных кластеров существенно отличались. Задача кластеризации относится к статистической обработке, а также к широкому классу задач обучения без учителя. Кластерный анализ
— это многомерная статистическая процедура, выполняющая сбор данных, содержащих информацию о выборке объектов, и затем упорядочивающая объекты в сравнительно однородные группы (кластеры)(Q-кластеризация, или Q-техника, собственно кластерный анализ). Кластер
— группа элементов, характеризуемых общим свойством, главная цель кластерного анализа — нахождение групп схожих объектов в выборке [9. с-3].
Реклама

Кластерный анализ применяют в различных областях человеческой деятельности: медицина, химия, психология, управление и во многом другом. Поэтому я считаю, что тема моего курсового проекта актуальна
.
В своей работе я ставлю ряд задач
:
1. Рассмотреть метод кластерный анализ как объект исследования
2. Понять, как помогает этот метод в социологических исследованиях
3. Научиться анализировать вопросник с помощью этого метода.
Кластерный анализ выполняет следующие основные задачи
:
Разработка типологии или классификации; исследование полезных концептуальных схем группирования объектов; порождение гипотез на основе исследования данных, проверка гипотез или исследования для определения, действительно ли типы (группы), выделенные тем или иным способом, присутствуют в имеющихся данных.
Глава 1. Кластерный анализ
Термин кластерный анализ, впервые введенный Трионом (Tryon) в 1939 году, включает в себя более 100 различных алгоритмов.
В отличие от задач классификации, кластерный анализ не требует априорных предположений о наборе данных, не накладывает ограничения на представление исследуемых объектов, позволяет анализировать показатели различных типов данных (интервальным данным, частотам, бинарным данным). При этом необходимо помнить, что переменные должны измеряться в сравнимых шкалах. [1. с-4]
Работа кластерного анализа опирается на два предположения. Первое предположение - рассматриваемые признаки объекта в принципе допускают желательное разбиение пула (совокупности) объектов на кластеры. Второе предположение - правильность выбора масштаба или единиц измерения признаков.
Методы кластерного анализа можно разделить на две группы:
1. иерархические;
2. неиерархические.
Каждая из групп включает множество подходов и алгоритмов.
Используя различные методы кластерного анализа, аналитик может получить различные решения для одних и тех же данных. Это считается нормальным явлением.
Рассмотрим иерархические и неиерархические методы подробно.
1.1.
Алгоритм кластерного анализа k-средних (k-means)
Наиболее распространен среди неиерархических методов алгоритм k-средних, также называемый быстрым кластерным анализом
. Полное описание алгоритма можно найти в работе Хартигана и Вонга (Hartigan and Wong, 1978). В отличие от иерархических методов, которые не требуют предварительных предположений относительно числа кластеров, для возможности использования этого метода необходимо иметь гипотезу о наиболее вероятном количестве кластеров.
Алгоритм k-средних строит k кластеров, расположенных на возможно больших расстояниях друг от друга. Основной тип задач, которые решает алгоритм k-средних, - наличие предположений (гипотез) относительно числа кластеров, при этом они должны быть различны настолько, насколько это возможно. Выбор числа k может базироваться на результатах предшествующих исследований, теоретических соображениях или интуиции.
Общая идея алгоритма
: заданное фиксированное число k кластеров наблюдения сопоставляются кластерам так, что средние в кластере (для всех переменных) максимально возможно отличаются друг от друга. [5. с-68-73]
1.1.1.Описание алгоритма
1
. Первоначальное распределение объектов по кластерам
.
Выбирается число, именуемое k, и эти точки считаются "центрами" кластеров. Каждому кластеру соответствует один центр.
Выбор начальных центров осуществляется следующим образом:
1. выбор k-наблюдений для максимизации начального расстояния;
2. случайный выбор k-наблюдений;
3. выбор первых k-наблюдений.
2
. Итеративный процесс
Вычисляются центры кластеров, которыми затем считаются покоординатные средние кластеров. Объекты перераспределяются.
Процесс вычисления центров и перераспределения объектов продолжается до тех пор, пока не выполнено одно из условий:
1. кластерные центры стабилизировались, т.е. все наблюдения принадлежат кластеру, которому принадлежали до текущей итерации;
2. число итераций равно максимальному числу итераций.
На рис. 1 приведен пример работы алгоритма k-средних для k, равного двум.
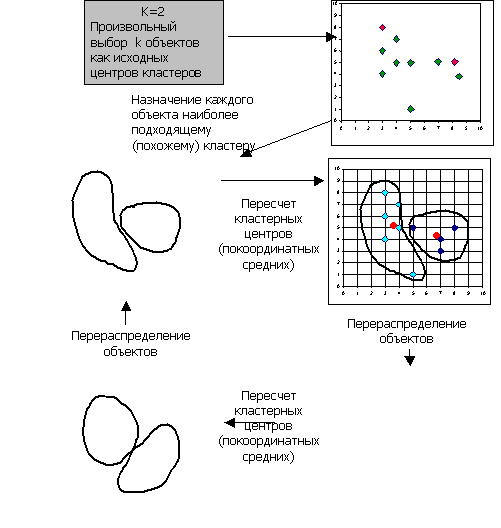
Рис. 1.
Пример работы алгоритма k-средних (k=2) [5. с-68-73]
1.1.2. Проверка качества кластеризации
После получений результатов кластерного анализа методом k-средних следует проверить правильность кластеризации (т.е. оценить, насколько кластеры отличаются друг от друга). Для этого рассчитываются средние значения для каждого кластера. При хорошей кластеризации должны быть получены сильно отличающиеся средние для всех измерений или хотя бы большей их части.
Достоинства алгоритма k-средних
:
1. простота использования;
2. быстрота использования;
3. понятность и прозрачность алгоритма.
Недостатки алгоритма k-средних
:
1. алгоритм слишком чувствителен к выбросам, которые могут искажать среднее. Возможным решением этой проблемы является использование модификации алгоритма - алгоритм k-медианы;
2. алгоритм может медленно работать на больших базах данных.
Возможным решением данной проблемы является использование выборки данных. [8. с-6]
1.2.
Алгоритм
PAM (partitioning around Medoids)
PAM является модификацией алгоритма k-средних, алгоритмом k-медианы (k-medoids). Алгоритм менее чувствителен к шумам и выбросам данных, чем алгоритм k-means, поскольку медиана меньше подвержена влияниям выбросов. PAM эффективен для небольших баз данных, но его не следует использовать для больших наборов данных.
1.3.
Сложности, возникающие при кластерном анализе
Как и любые другие методы, методы кластерного анализа имеют определенные слабые стороны, т.е. некоторые сложности, проблемы и ограничения.
При проведении кластерного анализа следует учитывать, что результаты кластеризации зависят от критериев разбиения совокупности исходных данных. При понижении размерности данных могут возникнуть определенные искажения, за счет обобщений могут потеряться некоторые индивидуальные характеристики объектов.
Существует ряд сложностей, которые следует продумать перед проведением кластеризации.
1. Сложность выбора характеристик, на основе которых проводится кластеризация. Необдуманный выбор приводит к неадекватному разбиению на кластеры и, как следствие, - к неверному решению задачи.
2. Сложность выбора метода кластеризации. Этот выбор требует неплохого знания методов и предпосылок их использования. Чтобы проверить эффективность конкретного метода в определенной предметной области, целесообразно применить следующую процедуру: рассматривают несколько априори различных между собой групп и перемешивают их представителей между собой случайным образом. Далее проводится кластеризация для восстановления исходного разбиения на кластеры. Доля совпадений объектов в выявленных и исходных группах является показателем эффективности работы метода.
3. Проблема выбора числа кластеров. Если нет никаких сведений относительно возможного числа кластеров, необходимо провести ряд экспериментов и, в результате перебора различного числа кластеров, выбрать оптимальное их число.
4. Проблема интерпретации результатов кластеризации. Форма кластеров в большинстве случаев определяется выбором метода объединения. Однако следует учитывать, что конкретные методы стремятся создавать кластеры определенных форм, даже если в исследуемом наборе данных кластеров на самом деле нет. [5. с-68-73]
1.4. Сравнительный анализ иерархических и неиерархических методов кластеризации
Неиерархические методы
выявляют более высокую устойчивость по отношению к шумам и выбросам, некорректному выбору метрики, включению незначимых переменных в набор, участвующий в кластеризации. Ценой, которую приходится платить за эти достоинства метода, является слово "априори". Аналитик должен заранее определить количество кластеров, количество итераций или правило остановки, а также некоторые другие параметры кластеризации. Это сложно начинающим специалистам.
Если нет предположений относительно числа кластеров, рекомендуют использовать иерархические алгоритмы кластерного анализа. Однако если объем выборки не позволяет это сделать, возможный путь - проведение ряда экспериментов с различным количеством кластеров, например, начать разбиение совокупности данных с двух групп и, постепенно увеличивая их количество, сравнивать результаты. За счет такого "варьирования" результатов достигается достаточно большая гибкость кластеризации.
Иерархические методы
, в отличие от неиерархических, отказываются от определения числа кластеров, а строят полное дерево вложенных кластеров. Сложности иерархических методов кластеризации: ограничение объема набора данных; выбор меры близости; негибкость полученных классификаций. Преимущество этой группы методов в сравнении с неиерархическими методами - их наглядность и возможность получить детальное представление о структуре данных.
Глава 2. Алгоритмы кластерного анализа
В последнее время ведутся активные разработки новых алгоритмов кластеризации, способных обрабатывать сверхбольшие базы данных. В них основное внимание уделяется масштабируемости. К таким алгоритмам относятся обобщенное представление кластеров (summarized cluster representation), а также выборка и использование структур данных, поддерживаемых нижележащими СУБД. Разработаны алгоритмы кластерного анализа, в которых методы иерархической кластеризации интегрированы с другими методами. К таким алгоритмам относятся: BIRCH, CURE, CHAMELEON, ROCK. [5. с-68-73]
2.1.
Алгоритм
BIRCH (Balanced Iterative Reducing and Clustering using Hierarchies)
Алгоритм предложен Тьян Зангом и его коллегами. Благодаря обобщенным представлениям кластеров, скорость кластеризации увеличивается, алгоритм при этом обладает большим масштабированием. В этом алгоритме реализован двухэтапный процесс кластеризации.
В ходе первого этапа формируется предварительный набор кластеров. На втором этапе к выявленным кластерам применяются другие алгоритмы кластерного анализа - пригодные для работы в оперативной памяти.
Если каждый элемент данных представить себе как бусину, лежащую на поверхности стола, то кластеры бусин можно "заменить" теннисными шариками и перейти к более детальному изучению кластеров теннисных шариков. Число бусин может оказаться достаточно велико, однако диаметр теннисных шариков можно подобрать таким образом, чтобы на втором этапе можно было, применив традиционные алгоритмы кластерного анализа, определить действительную сложную форму кластеров.
2.2. Алгоритм WaveCluster
WaveCluster представляет собой алгоритм кластеризации на основе волновых преобразований. В начале работы алгоритма данные обобщаются путем наложения на пространство данных многомерной решетки. На дальнейших шагах алгоритма анализируются не отдельные точки, а обобщенные характеристики точек, попавших в одну ячейку решетки. В результате такого обобщения необходимая информация умещается в оперативной памяти. На последующих шагах для определения кластеров алгоритм применяет волновое преобразование к обобщенным данным.
Особенности WaveCluster:
сложность реализации
алгоритм может обнаруживать кластеры произвольных форм
алгоритм не чувствителен к шумам
алгоритм применим только к данным низкой размерности
2.3. Алгоритмы кластерного анализа Clarans, CURE, DBScan
Алгоритм Clarans (Clustering Large Applications based upon RANdomized Search) формулирует задачу кластеризации как случайный поиск в графе. В результате работы этого алгоритма совокупность узлов графа представляет собой разбиение множества данных на число кластеров, определенное пользователем. "Качество" полученных кластеров определяется при помощи критериальной функции. Алгоритм Clarans сортирует все возможные разбиения множества данных в поисках приемлемого решения. Поиск решения останавливается в том узле, где достигается минимум среди предопределенного числа локальных минимумов.
2.4.
Алгоритм
CLARA (Clustering LARge Applications)
Алгоритм CLARA был разработан Kaufmann и Rousseeuw в 1990 году для кластеризации данных в больших базах данных. Данный алгоритм строится в статистических аналитических пакетах, например, таких как S+.
Изложим кратко суть алгоритма. Алгоритм CLARA извлекает множество образцов из базы данных. Кластеризация применяется к каждому из образцов, на выходе алгоритма предлагается лучшая кластеризация.
Для больших баз данных этот алгоритм эффективнее, чем алгоритм PAM. Эффективность алгоритма зависит от выбранного в качестве образца набора данных. Хорошая кластеризация на выбранном наборе может не дать хорошую кластеризацию на всем множестве данных. [9. с-3].
2.5. Итеративная кластеризация в SPSS
Обычно в статистических пакетах реализован широкий арсенал методов, что позволяет сначала провести сокращение размерности набора данных (например, при помощи факторного анализа), а затем уже собственно кластеризацию (например, методом быстрого кластерного анализа). Рассмотрим этот вариант проведения кластеризации в пакете SPSS.
Выбираем в меню: Analyze (Анализ) / Data Reduction (Преобразование данных) / Factor (Факторный анализ). При помощи кпопки Extraction (Отбор) следует выбрать метод отбора. Мы оставим выбранный по умолчанию анализ главных компонентов, который упоминался выше. Таже следует выбрать метод вращения - выберем один из наиболее популярных - метод варимакса. Для сохранения значений факторов в виде переменных в закладке "Значения" необходимо поставить отметку "Save as variables" (Сохранить как переменные).
В результате этой процедуры пользователь получает отчет "Объясненная суммарная дисперсия", по которой видно число отобранных факторов - это те компоненты, собственные значения которых превосходят единицу.
Полученные значения факторов, которым обычно присваиваются названия fact1_1, fact1_2 и т.д., используем для проведения кластерного анализа методом k-средних. Для проведения быстрого кластерного анализа выберем в меню Analyze (Анализ) / Classify (Классифицировать) / K-Means Cluster: (Кластерный анализ методом k-средних).
В диалоговом окне K Means Cluster Analysis (Кластерный анализ методом k-средних) необходимо поместить факторные переменные fact1_1, fact1_2 и т.д. в поле тестируемых переменных. Здесь же необходимо указать количество кластеров и количество итераций.
В результате этой процедуры получаем отчет с выводом значений центров сформированных кластеров, количестве наблюдений в каждом кластере, а также с дополнительной информацией, заданной пользователем.
Алгоритм k-средних делит совокупность исходных данных на заданное количество кластеров. Для возможности визуализации полученных результатов следует воспользоваться одним из графиков, например, диаграммой рассеивания. Традиционная визуализация возможна для ограниченного количества измерений, ибо, как известно, человек может воспринимать только трехмерное пространство. Если мы анализируем более трех переменных, следует использовать специальные многомерные методы представления информации, о них будет рассказано в одной из последующих лекций курса.
Итеративные методы кластеризации различаются выбором параметров:
1. начальной точки
2. правилом формирования новых кластеров
3. правилом остановки
В пакете SPSS, например, при необходимости работы как с количественными (например, доход), так и с категориальными (например, семейное положение) переменными, а также если объем данных достаточно велик, используется метод Двухэтапного кластерного анализа, который представляет собой масштабируемую процедуру кластерного анализа, позволяющую работать с данными различных типов.
На первом этапе работы записи предварительно кластеризуются в большое количество суб-кластеров. На втором этапе полученные суб-кластеры группируются в необходимое количество. Если это количество неизвестно, процедура сама автоматически определяет его. [5. с-75-77]
В общем случае все этапы кластерного анализа взаимосвязаны, и решения, принятые на одном из них, определяют действия на последующих этапах.
Аналитику следует решить, использовать ли все наблюдения либо же исключить некоторые данные или выборки из набора данных.
По мнению многих специалистов, выбор метода кластеризации является решающим при определении формы и специфики кластеров.
Анализ результатов кластеризации
. Этот этап подразумевает решение таких вопросов: не является ли полученное разбиение на кластеры случайным; является ли разбиение надежным и стабильным на под выборках данных; существует ли взаимосвязь между результатами кластеризации и переменными, которые не участвовали в процессе кластеризации; можно ли интерпретировать полученные результаты кластеризации.
Проверка результатов кластеризации
. Результаты кластеризации также должны быть проверены формальными и неформальными методами. Формальные методы зависят от того метода, который использовался для кластеризации.
Неформально включают следующие процедуры проверки качества кластеризации:
1. анализ результатов кластеризации, полученных на определенных выборках набора данных
2. кросс-проверка
3. проведение кластеризации при изменении порядка наблюдений в наборе данных
4. проведение кластеризации при удалении некоторых наблюдений
5. проведение кластеризации на небольших выборках
Один из вариантов проверки качества кластеризации - использование нескольких методов и сравнение полученных результатов. Отсутствие подобия не будет означать некорректность результатов, но присутствие похожих групп считается признаком качественной кластеризации. [2. с-2-3].
2.6. Кластеризация в Data Mining
Кластеризация в Data Mining приобретает ценность тогда, когда она выступает одним из этапов анализа данных, построения законченного аналитического решения. Аналитику часто легче выделить группы схожих объектов, изучить их особенности и построить для каждой группы отдельную модель, чем создавать одну общую модель на всех данных. Таким приемом постоянно пользуются в маркетинге, выделяя группы клиентов, покупателей, товаров и разрабатывая для каждой их них отдельную стратегию.
Очень часто данные, с которыми сталкивается технология Data Mining, имеют следующие важные особенности:
1. высокая размерность (тысячи полей) и большой объем (сотни тысяч и миллионы записей) таблиц баз данных и хранилищ данных (сверхбольшие базы данных)
2. наборы данных содержат большое количество числовых
и категорийных
атрибутов
Все атрибуты, или признаки объектов делятся на числовые
(numerical) и категорийные
(categorical). Числовые атрибуты – это такие, которые могут быть упорядочены в пространстве, соответственно категорийные – которое не могут быть упорядочены. Например, атрибут "возраст" – числовой, а "цвет" – категорийный. Приписывание атрибутам значений происходит во время измерений выбранным типом шкалы, а это, вообще говоря, представляет собой отдельную задачу.
Большинство алгоритмов кластеризации предполагают сравнение объектов между собой на основе некоторой меры близости (сходства). Мерой близости называется величина, имеющая предел и возрастающая с увеличением близости объектов. Меры сходства "изобретаются" по специальным правилам, а выбор конкретных мер зависит от задачи, а также от шкалы измерений. В качестве меры близости для числовых атрибутов очень часто используется евклидово расстояние
, вычисляемое по формуле
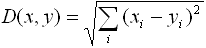
Для категорийных атрибутов распространена мера сходства Чекановского-Серенсена и Жаккара
. Потребность в обработке больших массивов данных в Data Mining привела к формулированию требований, которым должен удовлетворять алгоритм кластеризации:
· Минимально возможное количество проходов по базе данных
· Работа в ограниченном объеме оперативной памяти компьютера
· Работу алгоритма можно прервать с сохранением промежуточных результатов, чтобы продолжить вычисления позже
·Алгоритм должен работать, когда объекты из базы данных могут извлекаться только в режиме однонаправленного курсора
Алгоритм, удовлетворяющий данным требованиям (особенно второму), будем называть масштабируемым
(scalable). Масштабируемость
– важнейшее свойство алгоритма, зависящее от его вычислительной сложности и программной реализации. Алгоритм называют масштабируемым, если при неизменной емкости оперативной памяти с увеличением числа записей в базе данных время его работы растет линейно. На заре становления теории кластерного анализа вопросам масштабируемости алгоритмов внимания практически не уделялось. Предполагалось, что все обрабатываемые данные будут умещаться в оперативной памяти, главный упор всегда делался на улучшение качества кластеризации. Трудно соблюсти баланс между высоким качеством кластеризации и масштабируемостью. Поэтому в идеале в арсенале Data Mining должны присутствовать как эффективные алгоритмы кластеризации микромассивов (microarrays), так и масштабируемые для обработки сверхбольших баз данных (large databases).[10. с-7].
Глава 3. Опрос, посвященный психологическому состоянию личности
Я попросила ответить на предложенные вопросы 40 человек в возрасте от 18 до 60 лет.
Загружаем полученные данные в программу SPSS.
3.1. Факторный анализ
| Мера адекватности и критерий Бартлетта
|
| Мера выборочной адекватности Кайзера-Мейера-Олкина. |
,448 |
| Критерий сферичности Бартлетта |
Прибл. хи-квадрат |
539,764 |
| ст.св. |
190 |
| Знч. |
,000 |
| Матрица повернутых компонентa
|
| Компонента |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
| VAR00007 |
,918 |
| VAR00005 |
,726 |
| VAR00008 |
,706 |
| VAR00004 |
,698 |
| VAR00017 |
,930 |
| VAR00016 |
,792 |
| VAR00011 |
-,527 |
| VAR00014 |
,813 |
| VAR00013 |
,781 |
| VAR00012 |
,687 |
| VAR00015 |
,638 |
| VAR00020 |
,928 |
| VAR00019 |
,901 |
| VAR00018 |
,585 |
,652 |
| VAR00009 |
,811 |
| VAR00010 |
,749 |
| VAR00002 |
,876 |
| VAR00003 |
,779 |
| VAR00001 |
-,757 |
| VAR00006 |
,702 |
Метод выделения: Анализ методом главных компонент.
Метод вращения: Варимакс с нормализацией Кайзера.
|
| a. Вращение сошлось за 9 итераций. |
Из матрицы компонент видно, что вопросы под номерами 11, 10, 9, 18, 19, 17, 16, 20 сочетаются и, когда их обработать, вырисовывается определенная картина моей анкеты. Тоже самое можно сказать про вопросы под номерами 5, 7, 8, 4, 13, 12, 6, 14. Эти группы вопросов ясно вырисовывают нам психологический портрет интервьюера.
Проведенные мною исследования показали, что психологическое состояние личности на прямую зависит от потребностей и привязанностей данной личности.
Люди, выбирающие агрессивные виды спорта, настаивающие только на своем мнении в споре, те, кто не уступает место на дороге и в жизни ведут себя агрессивно и не уступают оппоненту.
Личности же с мягким характером, наоборот выбирают танцы, музыку, готовы уступать оппоненту и прощать обидчиков, пропускать все автомобили, находящиеся вместе с ним на дороге.
Выявился интересный факт: интервьюеры, не удовлетворенные своим социальным положением хотели бы жить вдалеке от людей, и наоборот, люди, находящиеся на вершине успеха, как можно больше времени хотят проводить в обществе.
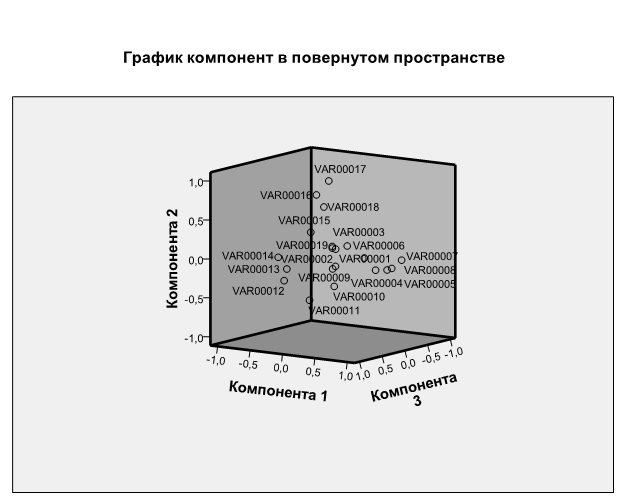
3.2. Быстрый кластерный анализ
| Начальные центры кластеров
|
| Кластер |
| 1 |
2 |
| VAR00001 |
1,00 |
2,00 |
| VAR00002 |
3,00 |
2,00 |
| VAR00003 |
3,00 |
2,00 |
| VAR00004 |
3,00 |
1,00 |
| VAR00005 |
3,00 |
1,00 |
| VAR00006 |
3,00 |
1,00 |
| VAR00007 |
2,00 |
1,00 |
| VAR00008 |
2,00 |
1,00 |
| VAR00009 |
2,00 |
3,00 |
| VAR00010 |
1,00 |
3,00 |
| VAR00011 |
1,00 |
3,00 |
| VAR00012 |
1,00 |
3,00 |
| VAR00013 |
1,00 |
3,00 |
| VAR00014 |
2,00 |
3,00 |
| VAR00015 |
2,00 |
1,00 |
| VAR00016 |
2,00 |
1,00 |
| VAR00017 |
2,00 |
1,00 |
| VAR00018 |
3,00 |
1,00 |
| VAR00019 |
3,00 |
1,00 |
| VAR00020 |
3,00 |
1,00 |
| Конечные центры кластеров
|
| Кластер |
| 1 |
2 |
| VAR00001 |
1,95 |
1,45 |
| VAR00002 |
2,11 |
2,05 |
| VAR00003 |
2,32 |
1,82 |
| VAR00004 |
2,42 |
1,82 |
| VAR00005 |
2,32 |
2,00 |
| VAR00006 |
2,26 |
2,14 |
| VAR00007 |
2,26 |
1,91 |
| VAR00008 |
2,11 |
2,32 |
| VAR00009 |
1,68 |
2,41 |
| VAR00010 |
1,74 |
2,41 |
| VAR00011 |
1,42 |
2,59 |
| VAR00012 |
1,32 |
2,27 |
| VAR00013 |
1,37 |
2,00 |
| VAR00014 |
1,74 |
2,09 |
| VAR00015 |
2,26 |
1,91 |
| VAR00016 |
2,47 |
1,55 |
| VAR00017 |
2,42 |
1,32 |
| VAR00018 |
2,16 |
1,36 |
| VAR00019 |
2,21 |
1,50 |
| VAR00020 |
2,16 |
1,59 |
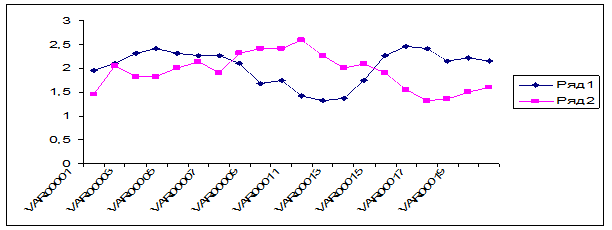
На графике видно, что кластерный анализ дал такие же результаты как и факторный. В результате проведенного анализа выделились две группы людей. Первая группа – спокойные, уравновешенные безконфликтные люди. Вторая – импульсивные и агрессивные личности. Такие же результаты показал и факторный анализ.
| Число наблюдений в каждом кластере
|
| Кластер |
1 |
19,000 |
| 2 |
22,000 |
| Валидные |
41,000 |
Приложение
1. Анкета, с помощью которой я смогу провести факторный анализ
1.
Я бы предпочел жить в доме, который находится:
1) в обжитом городе 2) нечто среднее 3) одиноко в глухих лесах
2. Я бы вполне мог жить один, вдали от людей.
1) да 2) иногда 3) нет
3. Когда я ложусь спать, я:
1) засыпаю быстро 2) нечто среднее 2) засыпаю с трудом
4. Если бы я вел машину по дороге, где много других автомобилей, я предпочел бы:
1) пропустить вперед большинство машин 2) не знаю 3) обогнать все идущие впереди машины
5. Я воздерживаюсь от критики людей и их высказываний:
1) да 2) иногда 3) нет
6. При общении с людьми я:
1) с готовностью вступаю в разговор 2) нечто среднее 3) предпочитаю спокойно оставаться в стороне
7. Я говорю о своих чувствах:
1) только если это необходимо 2) нечто среднее 3) охотно, когда представится возможность
8. После того как меня что-то сильно рассердит, я довольно быстро успокаиваюсь:
1) да 2) нечто среднее 3) нет.
9. Мне трудно говорить или декламировать перед большой группой людей:
1) да 2) нечто среднее 3) нет
10. Если кто-нибудь рассердится на меня, то я:
1) постараюсь его успокоить 2) нечто среднее 3) раздражаюсь
11. Встречаясь с несправедливостью, я скорее склонен забыть об этом, чем реагировать:
1) верно 2) не уверен 3) неверно
12. Бывают времена, когда у меня нет настроения видеть кого бы то ни было:
1) очень редко 2) нечто среднее 3) довольно часто
13. Мне важно, чтобы во всем, что меня окружает, не было беспорядка
1) верно 2) трудно сказать 3) неверно
14. Я бы скорее занимался (лась):
1) фехтованием и танцами 2) затрудняюсь сказать 3) борьбой и баскетболом
15. Меня раздражают люди, которые не могут быстро принимать решения.
1) верно 2) не знаю 3) неверно
16. Мои друзья чаще:
1) советуются со мной 2) дают мне советы 3) делают то и другое поровну
17. Мне бывает трудно признать, что я неправ.
1) да 2) иногда 3) нет
18. Худшее наказание для меня:
1) тяжелая работа 2) не знаю 3) быть запертым в одиночестве
19. Я принимаю решения:
1) быстрее, чем многие люди 2) не знаю 3) медленнее большинства людей
20. На меня большее впечатление производят:
1) мастерство и изящество 2) трудно сказать 3) сила и мощь
В этой таблице сведены все ответы интервьюеров, опрошенных мною.
2. Матрица, которая получилась после набивки анкеты
| 1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
| 1
|
1 |
2 |
3 |
2 |
1 |
3 |
1 |
3 |
2 |
1 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
1 |
1 |
| 2
|
2 |
1 |
3 |
4 |
2 |
1 |
3 |
2 |
1 |
2 |
3 |
1 |
1 |
2 |
3 |
2 |
1 |
2 |
2 |
2 |
| 3
|
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
| 4
|
1 |
1 |
1 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
3 |
1 |
1 |
2 |
1 |
| 5
|
1 |
1 |
2 |
2 |
3 |
1 |
3 |
2 |
2 |
2 |
1 |
1 |
1 |
1 |
3 |
3 |
3 |
1 |
1 |
1 |
| 6
|
3 |
2 |
2 |
1 |
1 |
1 |
2 |
2 |
2 |
3 |
3 |
3 |
3 |
2 |
2 |
2 |
1 |
1 |
1 |
2 |
| 7
|
1 |
2 |
2 |
2 |
2 |
2 |
1 |
1 |
1 |
3 |
3 |
3 |
1 |
2 |
2 |
1 |
1 |
1 |
3 |
3 |
| 8
|
1 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
1 |
1 |
1 |
1 |
| 9
|
1 |
1 |
1 |
2 |
2 |
3 |
3 |
3 |
2 |
2 |
2 |
2 |
2 |
2 |
1 |
1 |
1 |
2 |
3 |
2 |
| 10
|
1 |
1 |
2 |
2 |
2 |
2 |
3 |
3 |
2 |
2 |
2 |
1 |
1 |
1 |
2 |
3 |
3 |
2 |
2 |
2 |
| 11
|
1 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
2 |
2 |
2 |
2 |
2 |
2 |
1 |
1 |
1 |
2 |
2 |
| 12
|
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
2 |
2 |
2 |
1 |
1 |
1 |
1 |
1 |
| 13
|
2 |
2 |
2 |
2 |
2 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
| 14
|
2 |
2 |
2 |
2 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
1 |
1 |
1 |
1 |
1 |
| 15
|
2 |
2 |
2 |
2 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
| 16
|
2 |
2 |
2 |
2 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 17
|
1 |
1 |
1 |
3 |
3 |
3 |
3 |
3 |
2 |
2 |
2 |
2 |
2 |
3 |
3 |
3 |
3 |
1 |
1 |
1 |
| 18
|
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
2 |
2 |
2 |
2 |
2 |
| 19
|
1 |
2 |
2 |
2 |
2 |
3 |
3 |
3 |
1 |
1 |
1 |
1 |
1 |
1 |
3 |
3 |
3 |
3 |
3 |
3 |
| 20
|
2 |
2 |
2 |
1 |
1 |
1 |
1 |
1 |
3 |
3 |
3 |
3 |
3 |
3 |
1 |
1 |
1 |
1 |
1 |
1 |
| 21
|
2 |
2 |
2 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
| 22
|
1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
3 |
3 |
3 |
3 |
3 |
1 |
2 |
1 |
1 |
1 |
1 |
1 |
| 23
|
1 |
2 |
2 |
1 |
2 |
1 |
1 |
2 |
3 |
3 |
3 |
3 |
2 |
2 |
2 |
3 |
3 |
3 |
1 |
1 |
| 24
|
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
| 25
|
3 |
3 |
3 |
3 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
| 26
|
1 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
| 27
|
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
1 |
1 |
1 |
| 28
|
1 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 29
|
3 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
3 |
3 |
3 |
3 |
3 |
3 |
| 30
|
1 |
1 |
1 |
1 |
1 |
3 |
2 |
2 |
3 |
3 |
1 |
1 |
1 |
2 |
1 |
3 |
3 |
2 |
1 |
2 |
| 31
|
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
2 |
2 |
2 |
2 |
1 |
2 |
1 |
1 |
1 |
1 |
1 |
2 |
| 32
|
3 |
3 |
3 |
2 |
2 |
2 |
2 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
3 |
3 |
3 |
3 |
3 |
3 |
| 33
|
1 |
3 |
1 |
3 |
1 |
3 |
1 |
2 |
2 |
2 |
2 |
2 |
2 |
3 |
3 |
3 |
1 |
1 |
2 |
2 |
| 34
|
1 |
3 |
2 |
1 |
2 |
3 |
1 |
2 |
3 |
3 |
3 |
2 |
2 |
2 |
1 |
1 |
1 |
2 |
2 |
2 |
| 35
|
1 |
3 |
3 |
3 |
3 |
3 |
2 |
2 |
2 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
3 |
3 |
| 36
|
1 |
2 |
3 |
3 |
3 |
3 |
3 |
3 |
2 |
2 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
| 37
|
3 |
3 |
3 |
2 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
3 |
2 |
2 |
1 |
| 38
|
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
2 |
2 |
2 |
2 |
2 |
1 |
1 |
1 |
1 |
2 |
| 39
|
3 |
3 |
2 |
2 |
2 |
2 |
2 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
1 |
| 40
|
2 |
3 |
3 |
3 |
3 |
3 |
2 |
2 |
2 |
2 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
3 |
Заключение
Наступивший XXI век стал этапным для проникновения новых информационных технологий и создаваемых на их основе высокопроизводительных компьютерных систем во все сферы человеческой деятельности - управление, производство, науку, образование и т.д.
Кластерный анализ параллельно развивался в нескольких направлениях, таких как биология, психология, др., поэтому у большинства методов существует по два и более названий. Это существенно затрудняет работу при использовании кластерного анализа. Кластеризация служит для объединения больших объемов данных в группы (кластеры), которые характеризуются тем, что элементы внутри каждой группы имеют больше «сходства» между собой, чем между элементами соседних кластеров. В целом, все методы кластеризации можно подразделить на иерархические и неиерархические. Последние чаще всего используются при анализе больших объемов данных, т.к. они обладают большей скоростью. [12.http://www.intuit.ru/department/database/datamining/13/].[1]
Кластерный анализ не требует априорных предположений о наборе данных, не накладывает ограничения на представление исследуемых объектов, позволяет анализировать показатели различных типов данных (интервальным данным, частотам, бинарным данным). При этом нужно помнить, что переменные должны измеряться в сравнимых шкалах.
В ходе курсового проекта я подробно рассмотрела метод кластерный анализ.
Я доказала актуальность своей темы с помощью проведенного анкетирования.
В своем курсовом проекте я подробно рассмотрела алгоритм кластерного анализа, его виды.
Вначале своей работы я ставила ряд задач, которые в ходе работы, по моему мнению, были выполнены.
Кластерный анализ – один из наиболее интересных и действенных способов обработки информации.
Список используемых источников
1
. Статья в Интернет. Пакет статистической обработки. Кластерный анализ при большом количестве наблюдений.http://www.sati.archaeology.nsc.ru/stat/methods_info.php
2
. Итеративная кластеризация в SPSS. http://www.forekc.ru/nr2/index-iterativnaya_klasterizaciya_v_spss_2.htm
3
. Методы кластерного анализа. http://www.intuit.ru/department/database/datamining/13/
4
.Статья из журнала http://www.springerlink.com/content/qj16212n7537n6p3/fulltext.pdf
5
. Алгоритмы кластерного анализа. Статья в Интернет. «Анализ методов автоматического извлечения знаний из реляционных баз данных». Кошелева В. А. http://www.dea-analysis.ru/clustering-5.htm
6
.www.allbect.ru
7. Гаврилова Т.А.. Хорошевский В.Ф. - Базы знаний интеллектуальных систем (2000)
8
. http://www.learnspss.ru/handbooks.htmУчебник по работе с SPSS. Камалов Н. К.
9
. http://ru.wikipedia.org/wiki/Inf.htm. Извлечение информации
10
. http://www.basegroup.ru/library/analysis/clusterization/datamining/ Корчин А. П. Методы кластеризации
[1]
http://www.intuit.ru/department/database/datamining/13/ Методы кластерного анализа
|