МАТЕМАТИЧЕСКАЯ ЭКОНОМИКА
Понятия, результаты, методы М. э. удобно и принято излагать в тесной связи с их экономическим происхождением, интерпретацией и практическими приложениями. Особенно существенна связь с экономической наукой и практикой.
М. э. как часть математики начала развиваться только в 20 в. Ранее были лишь эпизодичные исследования, которые нельзя в строгом смысле отнести к математике.
В экономике присутствуют элементы управляемости и стихийности, жесткой определенности и существенной неоднозначности и свободы выбора, процессы технического характера и социальные процессы, где на первый план выдвигается поведение человека. Разные уровни экономики требуют существенно различного описания. Все это приводит к большой разнородности моделей математического Аппарата, а значит, и экономико-математических моделей задач.
Задача выявления оптимальных способов - одна из важнейших в экономике. Обычно предполагается, и это во многих случаях хорошо согласуется с действительностью, что Z -
выпуклый компакт. С помощью расширения пространства продуктов задача анализа эффективных способов при этом может быть сведена к случаю, когда Z -
выпуклый замкнутый конус.
Типичной задачей выявления эффективного способа является основная задача производственного планирования.
Эффективный рост. Ингредиенты, относящиеся к разным моментам или интервалам времени, формально можно считать различными. Поэтому описание производства в динамике в принципе укладывается в изложенную выше схему, состоящую из объектов {X, Z
, b}
, где X -
пространство ингредиентов, Z -
множество производственных возможностей, b -
задания требований и ограничений на экономику. Однако изучение собственно динамич. аспекта производства требует более специальных форм описания производственных возможностей.
Производственные возможности достаточно общей модели экономич. динамики задаются с помощью точечно-множественного отображения (многозначной функции) 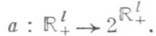 Здесь Здесь 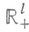 - (фазовое) пространство экономики, - (фазовое) пространство экономики,  интерпретируется как состояние экономики в тот или иной момент времени, где х k
-
количество продукта k, имеющегося в наличии в этот момент. Множество а(х).состоит из всех состояний экономики, в к-рые она может перейти за единичный временной интервал из состояния х.
Будем называть интерпретируется как состояние экономики в тот или иной момент времени, где х k
-
количество продукта k, имеющегося в наличии в этот момент. Множество а(х).состоит из всех состояний экономики, в к-рые она может перейти за единичный временной интервал из состояния х.
Будем называть
Реклама

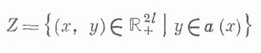
графиком отображения а. Точки ( х, у
).- допустимые производственные процессы.
Рассматриваются различные варианты задания возможных траекторий развития экономики.
С экономической точки зрения интерес представляют траектории, на которых достигается максимально возможный темп роста экономики, который она может выдержать сколь угодно долго. Оказывается, что при неизменных во времени а такие траектории являются стационарными, т. е. имеют вид
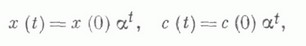
где а - темп роста (расширения) экономики. Стационарные эффективные в том или ином смысле, а также стационарные оптимальные траектории наз. магистралями.
При весьма широких предположениях имеют место теоремы о магистрали, утверждающие, что всякая эффективная траектория, независимо от начального состояния, с течением времени приближается к магистрали. Имеется большое число различных теорем о магистрали, различающихся определением эффективности или оптимальности, способом измерения расстояния до магистрали, типом сходимости, наконец, конечным или бесконечным временным интервалом.
Модель экономической динамики, у которой производственные возможности задаются многогранным выпуклым конусом, наз. моделью Неймана. Частным случаем модели Неймана является замкнутая модель Леонтьева, или (по другой терминологии) замкнутый динамический межотраслевой баланс (термин "замкнутый" используется здесь как характеристика свойства экономики, состоящего в отсутствии невоспроизводимых продуктов), который задается тремя матрицами с неотрицательными элементами Ф, А и В порядка 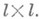
Модель Леонтьева также была сначала сформулирована в непрерывном времени в виде системы дифференциальных уравнений
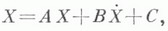
где X -
потоки продуктов, Аи В -
матрицы текущих и капитальных затрат соответственно, С -
потоки конечного потребления.
Эффективные и оптимальные траектории в моделях с непрерывным временем изучаются с помощью методов вариационного исчисления, оптимального управления, математич. программирования в бесконечномерных пространствах.
Математическая экономика имеет тесную связь с вычислительной математикой. Линейное программирование, линейные экономические модели оказали большое влияние на вычислительные методы линейной алгебры. По существу благодаря линейному программированию неравенства в вычислительной математике стали столь же употребительны, как и уравнения.
Реклама

Трудным и многоплановым вопросом является вычисление экономического равновесия. Напр., много работ посвящено условиям сходимости к равновесию системы дифференциальных уравнений

где р -
вектор цен, F -
функция избыточного спроса, т. е. разность функций спроса и предложения. Равновесные цены 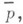 по определению, обеспечивают равенство спроса и предложения: по определению, обеспечивают равенство спроса и предложения: 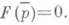
Функция избыточного спроса F задается либо непосредственно, либо через более первичные понятия соответствующей модели равновесия.
Экономическое равновесие, решение игры, решение той или иной экстремальной задачи могут быть определены как неподвижные точки подходящим образом сформулированного точечно-множественного отображения. В рамках исследований по М. э. разрабатываются численные методы поиска неподвижных точек разных классов отображений. Наиболее известен метод Скарфа, который является комбинацией идей леммы Шпернера и симплекс-метода решения задач линейного программирования.
|