Интересные примеры
в метрических пространствах:
1. В n
-
мерном евклидовом пространстве полная ограниченность совпадает с обычной ограниченностью, то есть с возможностью заключить данное множество в достаточно большой куб. Действительно, если такой куб разбить на кубики с ребром e, то вершины этих кубиков будут образовывать конечную 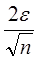 -сеть в исходном кубе, а значит, и подавно, в любом множестве, лежащем внутри этого куба.
1.
Единичная сфера S
в пространстве l
2
дает нам пример ограниченного, но не вполне ограниченного множества. Рассмотрим в S
точки вида:
е
1
=(1, 0, 0, ..., 0, 0, ...),
е
2
=(0, 1, 0, ..., 0, 0, ...),
…………………………,
е
n
=(0, 0, 0, ..., 1, 0, ...),
………………………….
Расстояние между любыми двумя точками е
n
и е
м
(n
¹
m
) равно Ö2. Поэтому последовательность {е
i
} и любая ее подпоследовательность не сходятся. Отсюда в S
не может быть конечной e-сети ни при каком e<Ö2/2.
2. Рассмотрим в l
2
множество П
точек
x=(x1
, x2
, ¼, xn
, ...),
удовлетворяющих условиям:
| x1
|£1, | x2
|£1/2, ¼,| xn
|£1/2n
-1
, ...
Это множество называется фундаментальным параллепипедом («гильбертовым кирпичем») пространства l
2
. Оно представляет собой пример бесконечномерного вполне ограниченного множества. Для доказательства его полной ограниченности поступим следующим образом.
Пусть e>0 задано. Выберем n
так, что 1/2n-1
<e/2. Каждой точке x=(x1
, x2
, ¼, xn
, ...)
из П
сопоставим точку x*=(x1
, x2
, ¼, xn
, 0, 0, ...)
из того же множества. При этом
r(x,x*)=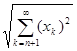 £ 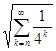<1/2n
-1
<e/2.
Множество П*
точек вида x*=(x1
, x2
, ¼, xn
, 0, 0, ...) из П
вполне ограничено (как ограниченное множество в n
-мерном пространстве). Выберем в П*
конечную e/2-сеть. Она будет в то же время e-сетью во всем П
. Докажем это.
Доказательство
: для "e>0, выберем n
так, что 1/2n
-1
<e/2.
"xÎП
: x=(x1
, x2
, ¼, xn
, ...) сопоставим
x*=(x1
, x2
, ¼, xn
, 0, 0, ...) и x*ÎП
. При этом r(x,x*)<e/2. Из пространства П
выберем x**: r(x*,x**)<e/2.
Тогда: r(x,x**)£r(x,x*)+r(x*,x**)<e/2+e/2=e.
Множество П*
содержит точки вида x*=(x1
, x2
, ¼, xn
, 0, 0, ...), в этом множестве выберем конечную e/2-сеть. Она будет e-сетью в пространстве П
, так какr(x,x**)<e.
|
