Содержание
- Исходные данные.
- Разработка схемы балочной клетки
- Сбор нагрузок на 1 м2
настила
- Расчет балки настила
- Расчет главной балки
- Расчет прикрепления балки настила к главной балке
- Расчет колонны
2. Разработка схемы балочной клетки
Нормальная схема балочной клетки

Разрез 1 - 1

3. Сбор нагрузок на 1 м2
настила
Таблица 1
Нагрузка на 1 м2
настила

4. Расчет балки настила Б1
4.1 Расчетная схема

4.2 Сбор нагрузок
Нагрузка на 1 погонный метр балки:
1.
Нормативная:
Нагрузка от собственного веса 1 погонного метра балки qс.в
= 0,100 т/м.
qн
= gн
* a + qс.в
= 2,60*1,9+0,100 = 5,61 т/м
2.
Расчетная:
Коэффициент надежности по нагрузке γf
= 1,05.
q = g* a + qс.в
* γf
= 3,46*1,9+0,100*1,05 = 6,68 т/м
4.3 Статический расчет
Максимальный расчетный изгибающий момент (в середине пролета)
Мmax
= q * l2
/ 8 =6,68 *5,72
/ 8 = 27,13 т*м
Максимальный нормативный изгибающий момент
Мн
max
= Мmax
* qн
/ q = 27,13*5,61/6,68 = 30,0 т*м
Максимальная расчетная поперечная сила (на опоре)
Qmax
= R = q * l / 2 = 6,68*5,7/2 = 19,04 т
4.4 Выбор материала
По таблице 50* СниП II – 23 – 81* для балок перекрытий, работающих при статических нагрузках, при отсутствии сварных соединений в условиях климатического района II5
выбираем сталь марки С245
(ГОСТ 27772 - 88).
Толщина полки двутавра ориентировочно tf
= 2– 20 мм.
По таблице 51* СниП II – 23 – 81* для стали марки С245 при tf
= 2 – 20 мм расчетное сопротивление по пределу текучести Ry
= 2450 кг/см2
.
4.5 Подбор сечения
Требуемый момент сопротивления
Wx
тр
= Mmax
/ (Ry
*γc
*c1
)
Коэффициент условий работы (таблица 6* СНиП II – 23 – 81*) γc
= 1,0.
Коэффициент, учитывающий развитие пластических деформаций, с1
= с (так как в месте действия Mmax
и в непосредственной близости от него т < 0,5*Rs
).
Отношение площадей сечений полки и стенки ориентировочно Af
/ Aw
= 0,75 => с1
= с = 1,095 (таблица 66 СНиП II – 23 – 81*).
Wx
тр
= 27,1*105
/ (2450*1,0*1,095) = 1011,3 см3
Из условия Wx
≥ Wx
тр
= 1011 см3
принимаем двутавр 40Б3 с параллельными гранями полок по ТУ 14–2–24-72 с моментом сопротивления Wx
= 1020 см3
>Wx
тр
= 1011 см3
.
4.6 Геометрические характеристики сечения
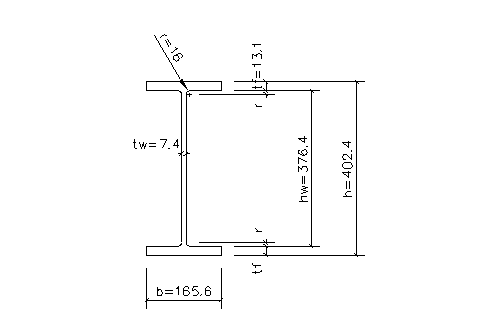 h = 402,4 мм; h = 402,4 мм;
b = 165,6 мм;
tw
= 7,4 мм;
tf
= 13,1 мм;
r = 16 мм;
A = 73,4 см2
;
Масса 1 м длины = 57,6 кг;
Реклама

Ix
= 20480 см4
;
Wx
= 1020 см.
Высота стенки hw
= h – 2*tf
= 402,4-2*13,1 = 376,4 мм;
Расчетная высота стенки hе
f
= hw
– 2*r = 376,4-2*16 = 344,4 мм.
Условная гибкость
Λ
w
= Λw
* √ Ry
/ E
Λw
= hе
f
/ tw
= 344,4/7,4 = 46,54
Λ
w
= 46,54*√ 2450 / (2,1*106
) = 1,59 < 2,2
Af
= tf
* b = 1,31*165,6 = 21,7 см2
Aw
= hw
* tw
= 37,64*0,74 = 27,85 см2
Af
/ Aw
=21,7 / 27,85 = 0,78
4.7 Проверка принятого сечения
1.
По прочности (I группа предельных состояний)
Условное нормальное напряжение при упругой работе балки (в пролете) Wey
= c1
* Wx
c1
= c = 1 + (1 – ξ2
) / (2 + 12* Af
/ Aw
) = 1+(1-0,22
)/(2+12*0,78) = 1,085
Минимальная относительная высота упругой зоны, соответствующая максимальной остаточной деформации, допускаемой нормами СНиП II – 23 – 81* ξ = 2*d / h = 0,2.
σ = Mmax
/ (c1
* Wx
) = 27,1*105
/ (1,085*1020) = 2448 кг/см2
<Ry
* γc
= 2450 кг/см2
→ прочность обеспечена.
Недонапряжение (2450-2448) / 2450 *100% = 0,08%.
а)
Разница между весом 1 м балки (57,6 кг) и его значением, принятым предварительно, составляет 0,87% от полной нагрузки q на балку ((100-57,6) /4850 *100% = 0,87%), поэтому уточнения величины q не производим.
б)
Так как недонапряжение составляет 0,1%< 5%, значит проверка двутавра с меньшей площадью не требуется.
Таким образом, окончательно принимаем двутавр 45Б3
по ТУ 14–2–24-72.
в)
Так как недонапряжение 0.1% < (с1
– 1)*100% = (1,09-1)*100% = 9%, то балка работает в упругопластической стадии.
Относительная высота упругого ядра ξФ
< 1
Максимальное нормальное напряжение (в середине пролета)
Касательное напряжение на опоре при этажном сопряжении
т = Qmax
/ Aw
= 19.04*103
/ 27.85 = 684 кг/см2
< Rs
* γc
= 0,58 * Ry
* γc
= 0,58*2450 = 1420 кг/см2
Касательное напряжение при сопряжении в одном уровне
т = Qmax
/ (0,8*Aw
) = 19*103
/ (0,8*27.85) = 855 кг/см2
< Rs
* γc
= 1420 кг/см2
Коэффициент, учитывающий ослабление болтами при сопряжении балок в одном уровне, 0,8.
2.
Местная устойчивость
Так как Λ
w
= 1,59 < 2,2, местную устойчивость проверять не будем.
3.
Общая устойчивость (I группа предельных состояний)
Обеспечена настилом, так как имеются соответствующие конструктивные элементы, связывающие настил с балкой.
4.
По деформативности при нормальных условиях эксплуатации (II группа предельных состояний)
Реклама

[ f / l ] = 1/250 (по таблице 40 СНиП II – 23 – 81*).
f / l = Mн
max
* l / (10 * E * Ix
) = 22.8*105
*570 / (10*2,1*106
*20480) = 1/331 < [ f / l ] = 1/250
5. Расчет главной балки Б2
5.1 Расчетная схема
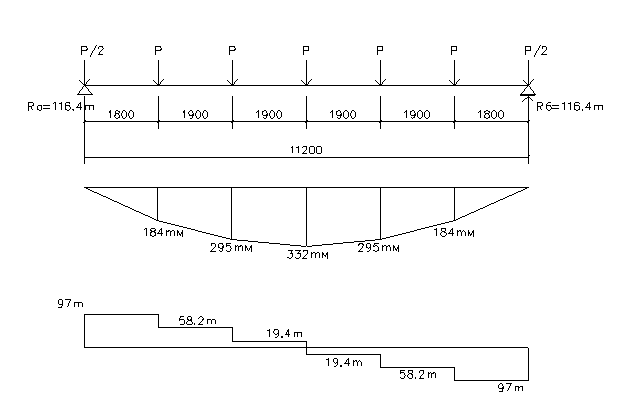
5.2 Сбор нагрузок
Р = Р' * 1,02 = q * l *1,02 = 6.68*5.7*1,02 = 38.8 т
Где коэффициент 1,02 учитывает собственный вес балки.
5.3 Статический расчет
При симметричной нагрузке:
RA
= RB
= ∑P / 2 = 6*P / 2 = 6*38.8/2 =116.4 т
Мx=а
= (RA
– 0,5*Р) * а’ = (116,4-0,5*38,8)*1,8 = 184 т*м
Мx=2*а
= (RA
– 0,5*Р) * (a’+ а) – Р*а = (116,4-0,5*38,8)*(1.8+1,9)-38,8*1,9 = 295 т*м
Мx=3*а
= (RA
– 0,5*Р) * (a’+2 * а) – Р*2*а - Р*а = (116,4-0,5*38,8)*(1.8+2*1,9)-38,8*2*1,9-38,8*1,9 = 332 т*м
Q max
= RA
– 0,5*Р = 116,4 – 0,5*38,8 = 97 т
Проверка величины Мmax
:
При распределенной нагрузке qБ2
= g * (l1
+ l2
) / 2*1,04 = (3,46*(5,7+5,7) / 2)*1,04 = 20,5т/м
Коэффициент, учитывающий собственный вес балки 1,04.
Мmax
' = qБ2
* L1
2
/ 8 = 20,8*11,22
/ 8 = 331 т*м = Мmax
= 332 т*м
5.4 Выбор материала
По таблице 50* СниП II – 23 – 81* для балок перекрытий, работающих при статических нагрузках, при отсутствии сварных соединений в условиях климатического района II5
выбираем сталь марки С235
(ГОСТ 27772 - 88).
Толщина полки двутавра ориентировочно tf
= 2 – 20 мм.
По таблице 51* СниП II – 23 – 81* для стали марки С235 при tf
= 2 – 20 мм расчетное сопротивление материала пояса по пределу текучести Ry
= 2350 кг/см2
.
5.5 Подбор основного сечения
Расчет ведем без учета пластических деформаций.
1.
Требуемый момент сопротивления сечения
Wx
тр
= Mmax
/ (Ry
*γc
) = 332*105
/(2350*1,0) = 13830 см3
2.
Условная гибкость
Λ
w
= Λw
* √ Ry
/ E
Гибкость стенки примем Λw
= hе
f
/ tw
= hw
/ tw
= 130
Λw
= 130*√ 2350 / (2,1*106
) = 4,35
3.
Оптимальная высота балки
hопт
' = 3
√ 1,5 * Wx
тр
* Λw
= 3
√ 1,5*13830*130 = 139,2 cм
Для балки переменного сечения оптимальная высота
hопт
≈ 0,95 * hопт
' = 0,95*139,2 = 132,2 см
Минимальная высота балки
hmin
= L1
* Ry
/ (107
* [f / l]) * qн
/ q = 11200*2350 / (107 *
1/400)*5,61 /6,68 = 88,4 см
[ f / l ] = 1/400 (по таблице 40 СНиП II – 23 – 81*).
Максимальная строительная высота перекрытия
hстр,
mах
= dн
– dб,
min
= 8,4-6,6 = 1,8 м
Максимальная высота при этажном сопряжении главных балок и балок настила
hm
ах
этажн
= hстр,
mах
– (tст
+ tпл
+ hБ1
) = 180-(2,5+10+40,3) = 127,2 см
hm
ах
одн ур
= hm
ах
этажн
+ hб1
= 127,2 +40,3 = 167,5см
Так как hm
ах
этажн
= 127,2 см < hопт
= 132,2 см, то этажное сопряжение не подходит.
Принимаем hб
= hопт
= 132,2 см
Условие hmin
= 88,4 см < hб
= 132,2 см < hm
ах
одн.ур
= 167,5 см выполнено.
Высота стенки hw
≈ 0,98 * hб
= 0,98*132,2 = 130 см
4.
Толщина стенки с учетом принятой гибкости
tw
= hw
/ Λw
= 130/130 = 1 cм
По условиям коррозионной стойкости tw
=1 cм > tw
= 0,6 см → условие выполнено.
По условию прочности в опорном сечении при работе на сдвиг
tw
=1 cм > tw
= 3/2 * Qmax
/ (hw
*Rs
) = 3/2*97*103
/ (130*1360) = 0,82 см → условие выполнено.
Rs
= 0,58 * Ry
= 0,58*2350 = 1360 кг/см2
Так как hw
= 1300 мм >1050 мм, то принимаем стенку из толстолистовой стали толщиной tw
=10 мм.
Площадь сечения стенки
Aw
= hw
* tw
= 130*1 = 130 см2
5.
Требуемая площадь пояса
Af
тр
= Wx
тр
/ hw
- hw
* tw
/ 6 = 13830/130 – 130*1/6 = 84,7 см2
Проверка сечения:
Af
,
min
тр
= 0,5 *( Amin
тр
- Aw
) = 0,5*(298,1-130) = 84,5 см2
Amin
тр
= 3 * Wx
тр
/ hопт
' = 3*15932/145,9 = 327,6 см2
По ГОСТ 82 – 70* принимаем сечение с размерами: tf
= 20 мм;
Требования:
а)
hw
/ 5 ≤ bf
≤ hw
/ 2,5
1300/5 ≤ bf
≤ 1300/2,5
260 мм ≤ bf
= 450 мм ≤ 520 мм → условие выполнено.
б)
При изменении сечения по ширине
bf
≥ 300 мм
bf
= 450 мм ≥ 300 мм → условие выполнено.
При изменении сечения по толщине
bf
≥ 180 мм
bf
= 450 мм ≥ 180 мм → условие выполнено.
в)
При изменении сечения по ширине
bf
≤ 30 * √ 2100 / Ry
* tf
bf
= 450 мм ≤ 30 * √ 2100 / 2350 * 20 = 567 мм → условие выполнено.
г)
tf
≤ 3 * tw
tf
= 20 мм ≤ 3 * 10 = 30 мм → условие выполнено.
д)
tf
= 20 мм → условие выполнено.
Окончательные размеры основного сечения:
стенка
Aw
=
hw
*
tw
= 130*1 = 130 см2
;
пояс
Af
=
tf
*
bf
= 2,0 * 45 = 90,0 см2
>
Af
тр
= 84,7 см2
6.
Геометрические характеристики основного сечения
hб
= hw
+ 2 * tf
= 130+2*2,0 = 134 см;
Af
= 90 см2
;
Aw
= 130 см2
;
А = 2 * Af
+ Aw
= 2*96+148,5 = 310 см2
;
Af
/ Aw
= 90 / 130 = 0,692;
Λ
w
= hw
/ tw
* √ Ry
/ E = 130 / 1*√2350 / (2,1*106
) = 4,35
Момент инерции стенки
Iw
= tw
* hw
3
/ 12 = 1*1303
/ 12 =183 *103
см4
;
Момент инерции поясов
2 * If
= 2*Af
* z2
= 2*90*662
= 784*103
см4
;
z = 0,5 * hw
+ 0,5 * tf
= 0,5*130+0,5*2,0 = 66 см
Момент инерции основного сечения
Iх
= Iw
+ 2 * If
= 183*103
+784*103
= 967 * 103
см4
;
Момент сопротивления сечения
Wx
= Ix
/ (0,5 * hб
) = 967*103
/ (0,5*134) = 14430 см3
> Wx
тр
= 13830 см3
.
5.6 Назначение размеров измененного сечения
Ширина измененного сечения
bf
'
= (0,5 – 0,6) * bf
=(0,5 – 0,6) * 450 = 225 – 270 мм
Принимаем bf
'
= 250 мм
Окончательные размеры измененного сечения:
стенка
Aw
=
hw
*
tw
= 130*1 = 130см2
;
пояс
A’
f
=
tf
*
bf
' = 2,0 * 25 = 50 см2
.
Геометрические характеристики сечения
hб
= hw
+ 2 * tf
= 130+2*2,0 = 134 см;
Af
' = 50 см2
;
Aw
= 130 см2
;
А' = 2 * Af
' + Aw
= 2*50+130 = 230 см2
;
Af
' / Aw
= 50 / 130 = 0,385;
Статический момент пояса
Sf
' = Af
' * z = 50*66 = 3300 cм3
;
Статический момент половины сечения
S0,5
' = Sf
' + S0,5*w
= Sf
' + 0,5 * 0,25 * tw
* hw
2
= 3300+0,5*0,25*1*1302
= 5410 cм3
;
Момент инерции стенки
Iw
= tw
* hw
3
/ 12 = 1*1303
/ 12 = 183 *103
см4
;
Момент инерции поясов
2 * I’f
= 2*Af
'
* z2
= 2*50*662
= 436 *103
см4
;
Момент инерции измененного сечения
Iх
’= Iw
+ 2 * I’f
= 183*103
+436*103
= 619 * 103
см4
;
Момент сопротивления измененного сечения
Wx
= Ix
' / (0,5 * hб
) = 619*103
/ (0,5*134) = 9240 см3
.
Таблица 2
Геометрические характеристики сечений
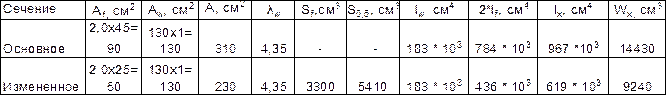
Основное сечение Измененное сечение

5.7 Определение места изменения сечения
Предельный изгибающий момент для измененного сечения в месте стыкового шва пояса
Расчетное сопротивление сварного шва сжатию, растяжению и изгибу по пределу текучести для полуавтоматической сварки и физических методов контроля качества шва Rwy
= Ry
= 2350 кг/см2
(по таблице 3 СНиП II – 23 – 81*).
[M] = Rwy
* Wx
' = 2350*9240 = 217*105
кг*см = 217 т*м
По эпюре изгибающих моментов (пункт 5.1) определяем, что сечения с изгибающим моментом М = 235 т*м находятся во II и V отсеках.
Положение сечений с М = 235 кг*м относительно опор А и В
МI
= ( RA
– 0,5 * P ) * Xлев
- P *( Xлев
– a) = [M] →
→ Xлев
= ( [M] – Ра )/ 1,5 * P = (217- 38,8*1,9)/ (1,5*38,8) = 2,46м
Так как нагрузка симметричная, то Xлев
= Xпр
= 2,46 м.
Сечения отстоят от ближайших ребер на
|2,46 – 1,90|= 0,56 м = 56 см > 10 * tw
= 10*1 = 10 см → прочность обеспечена.
5.8 Проверки принятых сечений
5.8.1.
По I группе предельных состояний
а)
Проверка прочности основного сечения по нормальным напряжениям в месте действия максимального момента
σ = Mmax
/ ( Wx
* γc
) = 332*105
/(14430*1,0) = 2320 кг/см2
< Ry
= 2350 кг/см2
→ прочность обеспечена
б)
Проверка прочности измененного сечения по касательным напряжениям на опоре
τ = 1,5 * Qmax
/ ( tw
* hw
) = 1,5*97*103
/ (1,0*130) = 1119 кг/см2
< Rs
= 1360 кг/см2
→ прочность обеспечена.
в)
Проверка прочности измененного сечения по приведенным напряжениям в месте изменения сечения
σ = M * 0,5 * hw
/ Ix
' = 217*105
* 0,5*130 / (619*103
) = 2280 кг/см2
τ = Qx
= х лев
/ ( tw
* hw
) = 58,2*103
/ (1*130) = 432 кг/см2
σпр
= √ σ2
+ 3 *τ2
= √ 22802
+4322
= 2350 кг/см2
< 1,15 * Ry
* γc
= 1,15*2350*1,0 = 2700 кг/см2
→ → прочность обеспечена
г)
Проверка общей устойчивости балки
Согласно пункту 5.16 СНиП II – 23 – 81* : lef
= a = 190 см;
b = bf
' = 25 см;
t = tf
' = 2 см;
h = 2* z = 2*66 = 132 см.
Расчетное сопротивление материала Ry
= 2350 кг/см2
.
lef
/ b ≤ ( 0,41 + 0,0032*b / t + ( 0,73 – 0,016 * b / t ) * b / h ) * √ Е / Ry
190/25 = 7,6 < (0,41+0,0032*25/2+(0,73-0,016*25/2)*25/132)*√2,1*106
/2350 = 16,4 → общая устойчивость обеспечена
5.8.2.
По II группе предельных состояний по деформативности при нормальных условиях эксплуатации
Коэффициент, учитывающий уменьшение жесткости балки вследствие перемены сечения, 0,9.
f / L = 0,1 *Mн
max
* L / ( 0,9 * E * Ix
) = 0,1 *Mmax
* L / ( 0,9 * E * Ix
) * qн
/ q =
= 0,1*332*105
*11.2*102
/ (0,9*2,1*106
*967*103
) * 5.61/6.68 = 1/588 < [ f / l ] = 1/400 → прочность обеспечена
5.9 Проверки местной устойчивости
5.9.1.
Проверка местной устойчивости пояса
bef
/ tf
≤ 0,5 * √ E / Ry
Величина неокаймленного свеса
bef
= 0,5*(45-1) = 22 см
22 / 2,0 = 11 < 0,5*√ 2,1*106
/ 2350 = 14,9 → устойчивость пояса обеспечена
5.9.2.
Проверка местной устойчивости стенки
а)
Расстановка ребер жесткости
Предусматриваем парные поперечные (вертикальные) ребра в местах опирания балок настила и на опорах.
Так как λw
= 4,35 > 3,2 , то согласно пункту 7.10 СНиП II – 23 – 81*, расстояние между ребрами
а = 190 (180) см < 2 * hef
= 2*130 = 260 см → условие выполнено.
б)
Определение размеров промежуточных ребер по СНиП II – 23 – 81*
Требуемая ширина
bh
тр
= hef
/30 + 40 = 1300/30+40 = 83.3 мм
Принимаем bh
=90 мм > bh
тр
=83.3 мм
Требуемая толщина ребра
ts
тр
= 2 * bh
* √ Ry
/ E = 2*90*√ 2350 / (2,1*106
) = 6,02 мм
Тогда bh
х ts
= 90 х 7 мм
Так как принято сопряжение на одном уровне, то размеры ребра : bh
= 110 мм;
ts
= 10 мм.
Принимаем bh
х ts
= 110 х 10 мм.
в)
Проверка местной устойчивости стенки
Так как λw
= 4,35 > 3,5, то проверяем местную устойчивость.
1. Проверка устойчивости стенки в I отсеке
При а/ hef
=190(180)/130=1.46(1,38)>1 расчётная длина lр
отс
= hef
=130см
Так как во I отсеке сечение балки не меняется, то вычисляем изгибающий момент М и поперечную силу Q на расстоянии Х1
= а – hw
/ 2 = 1,8 – 0,5*1,30 = 1,15м.
Поперечная сила
Qх =
= 97 т
Изгибающий момент
Мх =1,15
= ( RA
– P / 2 ) * Х1
= Qmax
* x1
= 97*1,15 = 111,5 тм
Нормальное напряжение
σ = Mх =1,15
* 0,5 * hw
/ Ix
' = 111,5*105
* 0,5*130 / (619*103
) = 1171 кг/см2
Касательное напряжение
τ = Qx
= 1,155
/ ( tw
* hw
) = 97*103
/ (1,1*130) = 746 кг/см2
Нормальное критическое напряжение для I отсека
Ccr
= 30,0 (по таблице 21 СНиП II – 23 – 81*).
σcr
= Ccr
*Ry
/ λw
2
= 30,0*2350 / 4,352
= 3730 кг/см2
Касательное критическое напряжение для I отсека
Отношение большей стороны отсека к меньшей μ = a / hw
= 180/130 = 1,38.
Меньшая из сторон отсека d = hw
=130 см.
λef
= d / tw
* √ Ry
/ E = 130/1*√2350/(2,1*106
) = 4,35
τс
r
= 10,3 * ( 1 + 0,76 / μ2
) * Rs
/ λef
2
= 10,3*(1+0,76 / 1,382
)*1360 / 4,352
= 1035 кг/см2
Проверка устойчивости
√ ( σ / σcr
)2
+ ( τ / τcr
)2
= √ ( 1171 / 3730)2
+ ( 746 /1035 )2
= 0,786 < γс
= 1 → местная устойчивость в I отсеке обеспечена.
2. Проверка устойчивости стенки во II отсеке
Во II отсеке балка меняет сечение. В месте изменения сечения максимальное нормальное напряжение в стенке.
σ = Mх =2,47
* 0,5 * hw
/ Ix
' = 2044 кг/см2
τ = Qх=2,47
/ ( tw
* hw
) = 448 кг/см2
Так как рассчитываемый отсек имеет те же размеры, что и отсек I, кроме длины, не влияющей на расчет, считаем, что критические напряжения имеют те же значения, тогда:
√ ( 2044 / 3730)2
+ ( 448 / 1035 )2
= 0,55 < γс
= 1
3. Проверка устойчивости стенки в III отсеке
Устойчивость обеспечена, так как касательное напряжение t меньше.
5.10 Расчет поясных швов
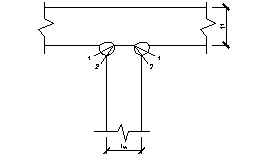
1 – 1 – сечение по металлу шва;
2 – 2 – сечение по металлу границы сплавления.
1.
Расчет по металлу шва.
Катет шва
Согласно пункту 12.8 СНиП II – 23 – 81* катет шва Kf
≤ 1,2 * tw
= 1,2*1 = 1,2 см.
По таблице 38* СНиП II – 23 – 81* для автоматической сварки при 17 мм < tf
= 20 мм < 22мм катет шва Kf
≥ 6 мм.
Принимаем минимально возможное значение Kf
= 6 мм.
По таблице 34* СНиП II – 23 – 81* принимаем автоматическую сварку в «лодочку» при диаметре проволоки d = 1,4 – 2 мм для катета шва Kf
= 6 мм.
Коэффициенты, учитывающие форму поперечного сечения шва βf
= 0,9;
βz
= 1,05.
Коэффициенты условий работы шва γwf
= γwz
= 1,0 (пункт 11.2 СНиП II – 23 – 81*).
По таблице 55* СНиП II – 23 – 81* для района II5
, 2-ой группы конструкций и стали С235 принимаем материалы дла сварки: флюс – АН – 348 – А ( по ГОСТ 9087 – 81*);
сварочная проволока СВ – 08А ( по ГОСТ 2248 – 70*).
Расчетное сопротивление углового шва срезу по металлу шва
Нормативное сопротивление металла шва по временному сопротивлению Rwun
= 4200 кг/см2
( по таблице 4* СНиП II – 23 – 81*).
Коэффициент надежности по металлу шва γwm
= 1,25 ( по таблице 3*, примечание 3, СНиПII–23–81*).
Rwf
= 0,55 * Rwun
/ γwm
= 0,55*4200/1,25 = 1850 кг/см2
Расчетное сопротивление по металлу границы сплавления
Временное сопротивление стали разрыву Run
= 3600 кг/см2
(по таблице 51* СНиП II – 23 – 81*).
Rwz
= 0,45 * Run
= 0,45*3600 = 1620 кг/см2
Условие (*)
1,0 ≤ Rwf
/ Rwz
≤ βz
/ βf
(*)
1,0 < 1848/1620 = 1,14 < 1,05/0,9 = 1,17 → условие выполнено.
Так как условие выполнено, то материал для сварки подобран правильно.
Проверка прочности по металлу шва
Сдвигающее усилие на единицу длины:
T = Qmax
* Sf
' / Ix
' = 97*103
* 3300 / (619*103
) = 517 кг.
τf
= T / (2 * βf
* Kf
) = 517 / (2*0,9*0,6) = 478 кг/см2
< Rwf
* γwf
* γc
= 1850*1,0*1,0 = 1850 кг/см2
→ прочность по металлу шва обеспечена.
2.
Расчет по металлу границы сплавления.
Так как условие (*) выполнено, и прочность по металлу шва обеспечена, то при γwf
= γwz
= 1,0 расчет прочности по металлу границы сплавления даст заведомо положительный результат.
5.11 Расчет опорных ребер
5.11.1.
Конструкция ребер на опорах А и Б.
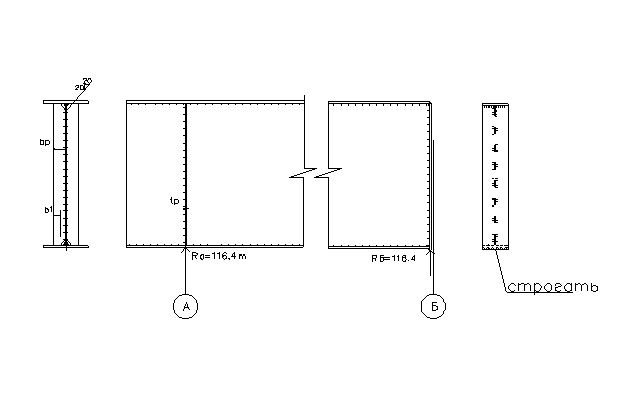
5.11.2.
Определение размеров опорных ребер из условия прочности на смятие.
Требуемая ширина ребра на опоре по оси А
bр
тр
= (bf
' – tw
) / 2 = (25-10) / 2 = 12 см = 120 мм
Принимаем bр
= 120 мм.
Длина площадки смятия ребра
b1
= 1 / 2 *(bf
' – 2 *2,0 - tw
) = 1/2 *(25-2*2,0-1,0) = 10 см
Требуемая толщина ребра по оси А из условия прочности на смятие
Коэффициент надежности по материалу γm
= 1,025 (по таблице 2* СНиП II – 23 – 81*).
Расчетное сопротивление смятию торцевой поверхности при наличии пригонки
Rp
= Run
/ γm
= 3600/1,025 = 3512,2 кг/см2
.
tp
тр
= RA
/ (Rp
* 2 * b1
) = 116*103
/ (3512,2*2*10) = 1,58 см
По ГОСТ 82 – 70* принимаем tp
= 1,6 см > tp
тр
= 1,58 см.
Для ребра по оси Б назначаем такую же толщину tp
= 1,6 см, а ширину bр
= bf
' = 25 см, тогда площадь смятия для этого ребра будет больше, чем по оси А, и прочность на смятие заведомо обеспечена.
5.11.3.
Расчет опорных ребер на устойчивость в плоскости, перпендикулярной стенке.
S = 0,65 * tw
* √ E / Ry
= 0,65*1,0*√2,1*106
/2350 = 19,4 см
Так как расчетное сечение по оси Б имеет меньшую площадь, то проверяем устойчивость ребра по оси Б.
A = S * tw
+ bf
' * tp
= 19,4*1,0+25*1,6 = 59,4 см2
Ix
= tp
* (bf
')3
/12 = 1,6*253
/ 12 = 2083 см4
ix
= √ Ix
/ A = √ 2083 / 59,4 = 5,92 см
λx
= hw
/ ix
= 130/5,92 = 22
φ ≈ 0,956 (по таблице 72* СНиП II – 23 – 81*)
σ = RБ
/ (φ * А) = 116*103
/ (0,956*59,4) = 1960 кг/см2
< Ry
= 2350 кг/см2
→ устойчивость опорных ребер обеспечена.
5.11.4.
Расчет сварного шва, соединяющего спарное ребро по оси Б со стенкой.
По таблице 34* СНиП II – 23 – 81* принимаем полуавтоматическую сварку в углекислом газе проволокой диаметром d < 1,4 мм при нижнем положении шва.
Коэффициенты, учитывающие форму поперечного сечения шва βf
= 0,7;
βz
= 1,0.
Коэффициенты условий работы шва γwf
= γwz
= 1,0 (пункт 11.2 СНиП II – 23 – 81*).
По таблице 55* СНиП II – 23 – 81* для района II5
, 2-ой группы конструкций и стали С235 принимаем сварочную проволоку СВ – 08Г2С ( по ГОСТ 2246 – 70*).
Расчетное сопротивление углового шва срезу по металла шва
Нормативное сопротивление металла шва по временному сопротивлению Rwun
= 5000 кг/см2
(по таблице 4* СНиП II – 23 – 81*).
Коэффициент надежности по металлу шва γwm
= 1,25 ( по таблице 3*, примечание 3 , СНиП II – 23 –81*).
Rwf
= 0,55 * Rwun
/ γwm
= 0,55*5000/1,25 = 2200 кг/см2
Расчетное сопротивление по металлу границы сплавления
Rwz
= 0,45 * Run
= 0,45*3600 = 1620 кг/см2
Условие (*)
1,0 ≤ Rwf
/ Rwz
≤ βz
/ βf
1,0 < 2200/1620 = 1,36 < 1,0/0,7 = 1,43 → условие выполнено.
Требуемая высота катета шва
Kf
тр
= √ RБ
/ (2 * 85 * βf
2
* Rwf
) = √ (116 *103
) / (2*85*0,72
*2200) = 0,775 см
Принимаем Kf
= 0,8 см > Kf
тр
= 0,775 см.
При tp
= 16 мм Kf
= 0,8 см > Kf
,
min
= 0,5 см и Kf
= 0,8 см < Kf
,
mах
= 1,2 * tw
= 1,2*1 = 1,2 см → условие выполнено.
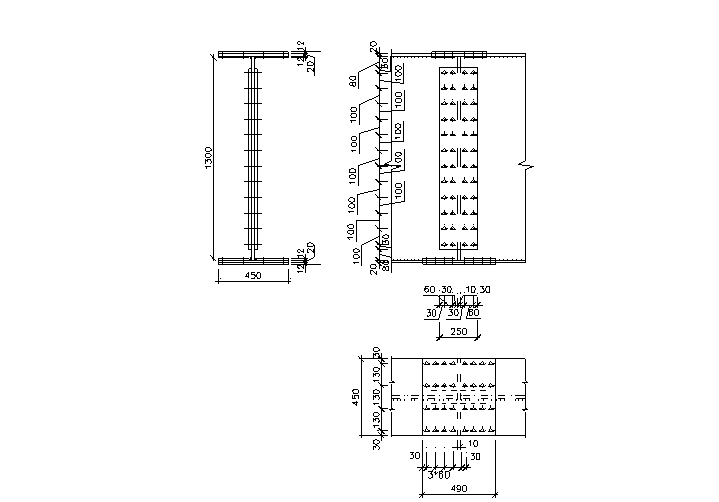
5.12 Расчет монтажного стыка на высокопрочных болтах
5.12.1.
Предварительная разработка конструкции.
Предварительно принимаем диаметр высокопрочных болтов db
= 20 мм.
Площадь сечения нетто болта Abn
= 2,45 см2
.
Диаметр отверстия
d = db
+ 3 = 20+3 = 23 мм.
Из конструктивных соображений принимаем толщину накладки для стенки tн
= tw
=1,0 см.
Зазор между отправочными марками в стыке 10 мм.
Число вертикальных рядов в стенке по одну сторону от стыка n = 2.
Минимальное расстояние между рядами
2,5 * d = 2,5*23 = 57,5 мм ≈ 60 мм.
Расстояние от края стенки или накладки до ближайшего ряда
1,3 * d = 1,3*23 = 29,9 мм ≈ 30 мм.
Шаг болтов по вертикали
/ 4 + 6 / * d = /4 + 6/*23 = 92 + 138 мм.
Шаг болтов принимаем 100 мм.
Расстояние между крайним болтом в вертикальном ряду и внутренней гранью пояса
60 мм < с = 100 < 120 мм.
Толщина накладок в поясе > 0,5 * tf
= 0,5*2,0 = 1,2 см.
Расстояние между внутренними накладками d1
≥ 40 мм.
Для пояса принимаем четырехрядное расположение болтов.
5.12.2.
Определение места стыка.
Момент инерции ослаблений (отверстиями) сечения пояса
If
осл
= Af
осл
* z2
= 4 * d * tf
* z2
= 4*2,3*2,0*66,02
= 80,2 * 103
см4
Момент инерции ослаблений сечения стенки
∑ li
2
= l1
2
+ l2
2
+ l3
2
+ l4
2
+ l5
2
= 102
(12
+32
+52
+72
+92
+112
) = 28600см2
Iw
осл
= 2 * d * tw
* (∑ li
/ 2)2
= d * tw
* ∑ li
2
/ 2 = 2,3*1*28600 / 2 = 32,9 * 103
см4
Момент инерции ослаблений всего сечения
Iосл
= 2 * If
осл
+Iw
осл
= (2*80,2+32,9)*103
= 193 * 103
см4
Момент инерции сечения с учетом ослаблений (нетто)
In
= Ix
– Iосл
= (967-193)*103
= 774 * 103
см4
Так как In
/ Ix
= 774 * 103
/ (967 * 103
) = 0,80 < 0,85, то в соответствии с п. 11.14 [I] условный момент инерции сечения нетто
Iс
= 1,18*In
= 1,18*774 * 103
=913*103
см4
Условный момент сопротивления
Wc
= Ic
/ (0,5 * hб
) = 913*103
/ (0,5*134) = 13630 см3
Предельный изгибающий момент в месте монтажного стыка
[M] = Wc
* Ry
= 13630*2350 = 320 * 105
кг*см = 320 т*м
По эпюре изгибающих моментов определяем, что сечение с изгибающим моментом, равным предельному ([M] = 320 т*м), находится во III и IV отсеках. Принимаем, что стык будет в III отсеке.
Положение стыка
Из уравнения МIII
для III определим положение стыка Xст
МIII
= (RA
– 0,5*Р) Xст
– Р(Xст
-а)- Р(Xст
-2а) = [М]
2,0Р* Xст
–2* Р* Xст
+3*Ра = [М]
Xст
= ([М]- 3*Р*а)/0,5Р = (320-3*38,8*1,9)/0,5*38,8=5,09 м. Расстояние от ближайшего поперечного ребра жёсткости 0,91 м > 0,5 м. Окончательно принимаем стык на расстоянии Xст
= 5,09м.
Внутренние усилия в месте стыка: изгибающий момент Мх=5,09
= 320 т*м;
поперечная сила Qх=5,09
= 19,4 т.
5.12.3.
Расчет стыка стенки.
Момент, воспринимаемый стенкой
Момент инерции стенки с учетом ослаблений (нетто)
Iwn
= Iw
– Iw
осл
= (183-32,9)*103
= 150,1 * 103
см4
Mw
= Мх=5,47
* Iwn
/ In
= 320*150,1*103
/ (774*103
) = 62,0 т*м
Поперечная сила, воспринимаемая стенкой
Qw
= Qх=5,09
= 19,4 т.
Усилие, приходящее0ся на крайний болт вертикального ряда от момента Mw
NM
= Mw
* lmax
/ (n * ∑ li
2
) = 62*105
*110 / (2*28600) = 11920 кг
Усилие, приходящееся на крайний болт вертикального ряда от поперечной силы Qw
Число болтов в вертикальном ряду m = 12 шт.
NQ
= Qw
/ (n * m) = 19,4*103
/ 2*12 = 808кг
Суммарное усилие, приходящееся на крайний болт вертикального ряда
Nb
= √ NM
2
+ NQ
2
= √ 119202
+8082
= 11947 кг = 11,95 т
Предельное усилие многоболтового соединения, приходящееся на один болт
По таблице 61* СНиП II – 23 – 81* для высокопрочных болтов принимаем сталь 40Х «Селект».
Наименьшее временное сопротивление материала болта разрыву Rbun
= 11000 кг/см2
.
Количество плоскостей трения nтр
= 2.
Коэффициент условия работы соединения при количестве болтов ³ 10 γb
= 1,0 (пункт 11.13 СНиП II – 23 – 81*).
Коэффициент трения при газопламенном способе обработки соединяемых поверхностей μ = 0,42 (по таблице 36* СНиП II – 23 – 81*).
Коэффициент условия работы балки в месте стыка на высокопрочных болтах γс
= 1,0 (по таблице 6* СНиП II – 23 – 81*).
Коэффициент надежности при газопламенном способе обработки и регулировании натяжения болтов по моменту закручивания γh
= 1,12 (по таблице 36* СНиП II – 23 – 81*).
[Nb
] = 0,7 * Rbun
* nтр
* γb
* Abn
* μ * γс
* 1/γh
= 0,7*11,0*2*1,0*2,45*0,42*1,0*1/1,12 = 14,14т>Nb
=11,95т → условие выполнено.
(14,14 – 11,95) / 11,95 *100% =18 % » 20 % → условие выполнено.
5.12.4.
Расчет стыка пояса.
а)
Определение числа болтов в стыке пояса.
Момент, воспринимаемый поясами
Mf
= Mx
=5,09
– Mw
= 320-62 = 258 т*м
Продольное усилие в поясе
Nf
= Mf
/ (2 * z) = 258 / (2*0,66) = 196 т
Требуемое число болтов (по одну сторону от стыка)
nb
тр
= Nf
/ [Nb
] = 196/14,14 = 13,86 шт.
Принимаем 14 болтов.
б)
Проверка прочности накладок.
Пусть толщина накладок в поясе tн
= 12 мм > 0,5 * tf
= 0,5*20 = 10 мм.
Ширина наружной накладки bн
= bf
= 450 мм.
Ширина внутренней накладки
bн
' ≤ 0,5 * (bf
- 40) = 0,5*(450-40) = 205 мм
Принимаем bн
' = 200 мм.
Расстояние между внутренними накладками
d1
= bн
– 2 * bн
' = 450-2*200 = 50 мм > 40 мм → условие выполнено.
Площадь сечения накладок
Aн
= tн
* (bн
+2*bн
') = 1,2*(45+2*20) = 102 см2
> Af
= tf
* bf
= 2,0 * 45 = 90 см2
→ прочность накладок обеспечена.
Окончательно принятая конструкция
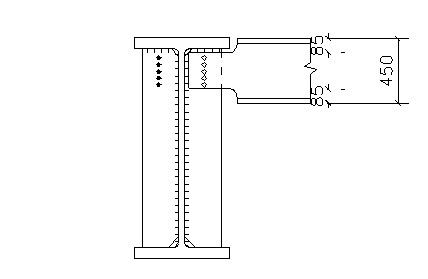
6. Конструкция и расчет прикрепления
балки настила к главной балке.
Принимаем по табл.57, что на балке настила присоединяется к ребру главной балки на болтах грубой точности класса 4.6.
Пусть диаметр болтов db
= 22 мм, а диаметр отверстия d = db
+ 3 = 22 + 3 = 25 мм.
Расчетное усилие, которое может быть воспринято одним болтом на срез, по формуле:
Nbs
= Rbs
*gb
*Ab
*ns
Nbs
= 1500*0.9*3.8*1 = 5130 кг,
Где Rbs
– расчетное сопротивление болтового соединения срезу;
gb
- коэффициент условий работы соединения в расчетах на срез,
Ab
= П*d2
b
/4 = 3.8 см2
– площадь сечения стержня болта брутто,
ns
- число расчетных срезов одного болта.
Расчетное усилие, которое может быть воспринято одним болтом при работе соединения на смятие, по формуле:
Nb
р
= Rb
р
*gb
*db
*Stmin
Nb
р
= 3550*0.9*2.2*0.76 = 5340 кг
Где Rb
р
– расчетное сопротивление болтового соединения смятию;
Stmin
- наименьшая суммарная величина элементов, сминаемых в одном направлении,
Stmin
= tw
= 0.76 см < ts
= 1.0 см, где tw
и ts
–толщина стенки балки настила и промежуточного ребра главной балки соответственно.
Количество болтов
n = 1.2*R/Nmin
= 1.2*18.2*103
/5130 = 4.25,
где R – величина опорной реакции балки настила,
1,2 – коэффициент, учитывающей влияние защемления в соединениях,
Nmin
– меньшее значение из величин Nbs
и Nbp
.
Принимаем 5 болтов. Так как значения a и b соответствуют требованиям, корректировать значение gb
при определении Nbp
не требуется.
Проверка стенки балки настила на срез по ослабленному отверстиями и вырезами сечению:
t = R/An
= 18.2 *103
/ 19.4 = 940 кг/см2
< Rs
*gs
= 1420*1 = 1420 кг/см2
7. Расчет колонны К1
7.1 Расчетная схема, определение нагрузки, статический расчет
Нагрузка на колонну
Коэффициент, учитывающий вес колонны, 1,005.
N = 2 * RБ
* 1,005 = 2*116*1,005 = 232 т
Приближенное значение нагрузки на колонну
Коэффициент, учитывающий вес балок и колонны, 1,04.
N = g * (L1
+ L2
) / 2 * (l1
+ l2
) / 2 * 1,04 = 3,46 * (11,2+11,2)/2 * (5,7+5,7)/2 * 1,04 = 230 т
Отметка верха колонны
Отметка настила (пола) площадки dн
= 8,4 м.
Толщина стяжки tстяжки
= 0,025 м.
Толщина железобетонной плиты tж/б плиты
= 0,10 м.
Высота сечения главной балки hгл.балки
= 1,34 м.
Величина выступа опорного ребра главной балки 0,015 м.
dв.к
= dн
– (tстяжки
+ tж/б плиты
+ hгл.балки
+ hБ1
+ 0,015) = 8,4-(0,025+0,10+1,34+0,015) = 6,92 м
Длина колонны
Отметка низа колонны dн.к
= -0,4 м
lк
= dв.к
– dн.к
= 6,92 – (-0,4) = 7,32 м
Расчетная схема колонны
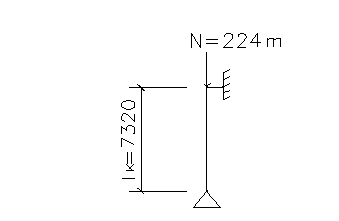
Расчетные длины относительно обеих главных осей
lx
= ly
= lef
= μ * lк
= 1 * 7,32 м
7.2 Подбор сечения и проверка устойчивости колонны
7.2.1.
Определение сечения вервей.
Принимаем сквозную колонну из двух прокатных швеллеров, соединенных планками.
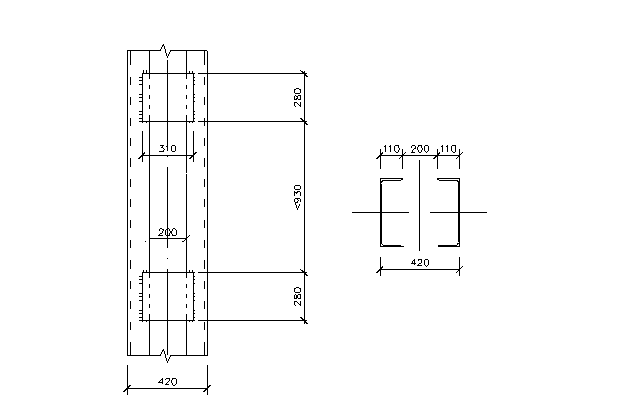
По таблице 50* СниП II – 23 – 81* для колонны К1, относящейся к 3-й группе конструкций, принимаем сталь марки С245
(ГОСТ 27772 - 88).
По таблице 51* СниП II – 23 – 81* для фасонного проката из стали марки С245 при толщине 4 – 20 мм расчетное сопротивление материала пояса по пределу текучести Ry
= 2450 кг/см2
.
Так как ослабления в колонне отсутствуют (Ан
= А), расчет на прочность не требуется; определяющим является расчет на устойчивость
Сечения ветвей из расчета на устойчивость относительно материальной оси Х – Х.
Задаемся гибкостью λх
з
= 60.
Коэффициент продольного изгиба центрально - сжатых элементов φх
з
= 0,805 (таблица 72* СниП II – 23 – 81*).
Требуемый радиус инерции
ix
тр
= lx
/ λх
з
= 732/ 60 = 12,2 см.
АВ
тр
= N / (2 * φх
з
* Ry
* γc
) = 232 * 103
/ (2*0,805*2450*1,0) = 56,8 см2
По сортаменту принимаем швеллер № 36 с площадью поперечного сечения АВ
= 53,4 см2
» АВ
тр
= 56,8 см2
Геометрические характеристики: АВ
= 53,4 см2
;
ix
= 14,2см; bf
= 11,0см; Iy
1
= 513 см4
; iy
1
= 3,1 см4
; z0
= 2,68 см;
tw
= 0,75 см; tf
= 1,26 см.
7.2.2.
Проверка устойчивости колонны относительно материальной оси Х – Х.
Гибкость стержня
Предельная гибкость [λ] = 120 (таблица 19* СниП II – 23 – 81*).
λх
= lx
/ ix
= 732/ 14,2 = 51,5 < [λ] = 120
Коэффициент продольного изгиба центрально-сжатого стержня φх
= 0,86 ( таблица 72*СниП II–23– 81*).
σ = N / (2 * AB
* φx
) = 232*103
/ (2*53,4*0,86) = 2430 кг/см2
< Ry
* γc
= 2450*1,0 = 2450 кг/см2
→ устойчивость колонны относительно материальной оси Х – Х обеспечена.
Недонапряжение (2450-2430) / 2450 *100% = 0,8%.
Окончательно принимаем 2 швеллера № 36
.
7.2.3.
Установление расстояния между ветвями.
Гибкость ветви относительно оси Y – Y.
λв
£λх
/ √2 = 51,5 / √2 = 36,5
Принимаем λв
= 30, тогда λy
тр
= √ λх
2
- λв
2
= √ 51,52
- 302
= 41,1 > λв
= 30
Требуемый радиус инерции
iy
тр
= ly
/ λy
тр
= 732/ 41,1 = 18,1 см.
Требуемое расстояние между центрами тяжести ветвей
стр
= 2 * √ (iy
тр
)2
- iy
1
2
= 2*√ 18,12
– 3,12
= 35,67 см
Требуемая ширина колонны
bк
тр
= cтр
+ 2 * z0
= 35,67+2*2,68 = 41,03 см
Приближенное значение ширины колонны (Коэффициент формы сечения α = 0,44.)
bк
тр
= iy
тр
/ α = 18,1 / 0,44 = 41,1 см
Принимаем bк
= 42 см.
Зазор между ветвями
d = bк
– 2 * bf
= 42 – 2*11 = 20 см > 10 см → условие выполнено.
Так как условие выполнено, оставляем принятый размер bк
= 42 см.
Расстояние между центрами тяжести ветвей
с = bк
– 2 * z0
= 42 – 2*2,68 = 36,67 см
7.2.4.
Проверка устойчивости относительно свободной оси Y – Y.
Iy
= 2 * (Iy
1
+ AВ
* (0,5 * с)2
) = 2 * (513 + 53,4*(0,5*36,7)2
) = 38850 см4
i
y
= √ Iy
/ (2 * AВ
) = √ 3 / (2*53,4) = 19,07 см > iy
тр
= 18,1 см → условие выполнено.
λy
= ly
/ iy
= 732 / 19,07 = 38,4 > λв
= 30 → условие выполнено.
Приведенная гибкость относительно свободной оси Y – Y.
λef
= √ λy
2
+ λв
2
= √ 38,42
+ 302
= 49,7 ≈ λx
= 50,7
Так как λef
= 49,7 < λx
=50,7 то φх
= 0,87 < φy
= 0,871 и устойчивость относительно оси Y – Y можно не проверять.
7.3 Расчет соединительных планок
7.3.1.
Установление размеров планок.
d = (0,5 – 0,75) * bк
= (0,5 – 0,75)*42 = 21 – 32 см
Принимаем d = 25 см.
Длина планки
bS
= d +2 * 4 = 21 + 2*4 = 29 см
Требования:
Принимаем t = 1.
d / t = 25 / 1 = 25 < 30 → условие выполнено.
bS
/ t = 29 / 1 = 29 < 50 → условие выполнено.
Так как условия удовлетворены, то выпучивания быть не должно.
Требуемое расстояние между планками
lВ
тр
= λв
*i
y1
= 30*3,1 = 93 см
Требуемое расстояние между осями планок
lтр
= lВ
тр
+ d = 93 + 25 = 118 см
IS
= t * d3
/ 12 = 1*253
/ 12 = 1300 см4
IВ
= Iy
1
= 513 см4
IS
* l / (IВ
* с) = 1300*118 / (513*37,64) = 7,82 > 5 → условие выполнено.
7.3.2.
Определение усилий в планках.
Фиктивная поперечная сила
Коэффициент β
Так как φх
= 0,87 < φy
= 0,871, то φmin
= φх
= 0,87.
φmin
/ φy
= 0,87 / 0,871 = 0,9999=1
N / (φy
* 2 * AB
* Ry
) = 224 * 103
/ (0,871*2*53,4*2450) = 0,975
Так как φmin
/ φy
= 1 > N / (φy
* 2 * AB
* Ry
) = 224*103
/ (0,871*2*53,4*2450) = 0,975 то β = 0,975.
Qfic
= 7,15 * 10-6
* 2 * AB
* E * β * (2330 * Ry
/ E – 1 ) =
= 7,15 * 10-6
* 2 * 53,4 * 2,1 * 106
* 0,975 * (2330 * 2450 / (2,1 * 106
) – 1) = 2690 кг
Приближенное значение фиктивной поперечной силы (в запас) по методу интерполяции
При Ry
= 2450 кг/см2
Q'fic
= (20 + (30 – 20) / (2600 – 2100) * (2450 – 2100)) * 2 * AB
=
= (20 + (30 – 20) / (2600 – 2100) * (2450 – 2100)) * 2 * 53,4 = 2880 кг
Поперечная сила, действующая в плоскости планок
QS
= Qfic
/ 2 = 2690 / 2 = 1345 кг
Сила, срезывающая одну планку
F = QS
* l / c = 1345*118 / 37,64 = 4220 кг
Момент, изгибающий планку в ее плоскости
М1
= QS
* l / 2 = 1345*118 / 2 = 79300 кг*см
7.3.3.
Проверка прочности приварки планок.
Предусматриваем использование ручной сварки при изготовлении колонны. Принимаем, что планки прикрепляются к полкам швеллеров угловыми швами с высотой катета Kf
= 8 мм < t = 10 мм с заводкой швов за торец на 20 мм.
По таблице 55* СниП II – 23 – 81* для района ll5
и стали марки С245 принимаем электроды марки Э42 (ГОСТ 9467 – 75).
Коэффициенты, учитывающие форму поперечного сечения шва βf
= 0,7; βz
= 1,0.
Коэффициенты условий работы шва γwf
= γwz
= 1,0 (пункт 11.2 СНиП II – 23 – 81*).
Rwf
= 1850 кг/см2
(таблица 56* СниП II – 23 – 81*).
Временное сопротивление для толщины проката 11см < tf
= 12,6 см < 20 мм Run
= 3700 кг/см2
(таблица 51* СниП II – 23 – 81*).
Rwz
= 0,45 * Run
= 0,45*3700 = 1665 кг/см2
1,1 < Rwf
/ Rwz
= 1850 / 1665 = 1,11 < βz
/ βf
= 1,0 / 0,7 = 1,43 → условие выполнено.
Напряжение в шве
τF
= F / (βf
* Kf
*a) = 4220 / (0,7*0,8*25) = 301 кг/см2
τМ
1
= 6 * М1
/ (βf
* Kf
*a2
) = 6*79300 / (0,7*0,8*252
) = 1360 кг/см2
Условие прочности шва
τ = √ τF
2
+ τM
1
2
= √ 3012
+ 13602
= 1390 кг/см2
< Rwf
* γwf
* γc
= 1850 * 1,0 * 1 = 1850 кг/см2
→ прочность шва обеспечена с большим запасом.
Уменьшаем катет шва до Kf
= 6 мм.
τ = 1390 *0,8/0,6 = 1850 кг/см2
< Rwf
* γwf
* γc
= 1850 * 1,0 * 1 = 1850 кг/см2
→ прочность обеспечена.
Прочность планок заведомо обеспечена, так как толщина планки t = 10 мм > Kf
= 6 мм.
7.4 Расчет базы
7.4.1.
Определение размеров плиты в плане.
Расчетное сопротивление смятию бетона фундамента.
Принимаем ξ = 3
√ Аф
/ Апл
= 1,2
Призменная прочность бетона М150 Rс
= 70 кг/см2
Rф
= ξ * Rс
= 1,2*70 = 84 кг/см2
Требуемая площадь плиты
Апл
тр
= N / Rф
= 232*103
/ 84 = 2760 см2
Ширина плиты из конструктивных соображений
Принимаем с = 5 см.
Впл
= hк
+ 2 * tтр
+ 2 * c = 36 + 2*1,0 + 2*5,0 = 48,0 см
Требуемая длина плиты
Lпл
тр
= Апл
тр
/ Впл
= 2760 / 48 = 57,5 см
Требуемая длина плиты из конструктивных соображений
Принимаем а1
= 100 мм (для размещения «плавающей» шайбы под гайки фундаментных болтов).
Lпл
тр
= bк
+ 2 * а1
= 42,0 + 2*10,0 = 62,0 см
Окончательно принимаем Lпл
= 62,0 см.
7.4.2.
Определение толщины плиты.
Плита работает на изгиб как пластинка, опертая на траверсы и торец стержня и нагруженная равномерно распределенным (условно) реактивным давлением фундамента.
q = N / (Впл
* Lпл
) = 232*103
/ (48*62) = 74,9 кг/см2
< Rф
= 84 кг/см2
Максимальные моменты для отдельных участков плиты
I участок (плита работает как пластинка, опертая по контуру)
Коэффициент, зависящий от отношения более длинной части стороны участка «а» к более короткой «b» α
а / b = 42/36 = 1,2 → α = 0,063
Мl
= α * q * b2
= 0,063*74,9*362
= 6115 кг*см
II участок (плита работает как пластинка, опертая по трем сторонам)
Коэффициент, зависящий от отношения закрепленной стороны «а1
» к незакрепленной «b1
» α1
а1
/ b1
= 10 / 36 = 0,28 < 0,5
Так как а1
/ b1
= 0,25 < 0,5, то плита работает как консоль вылетом а1
= 10 см.
Мll
= 0,5 * q * а1
2
= 0,5*74,9*102
= 3745 кг*см
III участок (плита работает как консоль)
Мlll
= 0,5 * q * с2
= 0,5*74,9*5,02
= 935 кг*см
По таблице 50* СниП II – 23 – 81* для плиты принимаем сталь марки ВСт3кп2 (ГОСТ 380 – 71*).
По таблице 51* СниП II – 23 – 81* для проката из стали марки ВСт3кп2 при толщине t = 21 – 40 мм расчетное сопротивление материала по пределу текучести Ry
= 2100 кг/см2
.
Требуемая толщина плиты
tпл
тр
= √ 6 * Mmax
/ (Ry
* γc
) = √ 6*6115 / (2100*1) = 4,18 см, так как толщина плиты превышает 4см введем дополнительное ребро на участке I.
Рассмотрим участок Iа:
а= hк
= 36см. b=0,5 bк
=0,5*42=21см;
a/b= 36/21=1,67; → α = 0,09
Мla
= 0,09 *74,9*212
= 2970 кг*см
Mmax
= Мll
= 3745 кг*см
tпл
тр
= √ 6 * Mmax
/ (Ry
* γc
) = √ 6*3745 / (2100*1) = 3,34 см
Принимаем tпл
= 36 мм > tпл
тр
= 33,4 мм.(ближайший больший стандартный размер)
7
.4.3.
Расчет траверсы.
Требуемая высота траверсы
При Kf
= 1,0 см < 1,2 * tтрав
= 1,2*1,0 = 1,2 см
hтрав
тр
= N / (4 * βf
* Kf
* Rwf
* γc
* γwf
) + 1,0 = 232*103
/(4*0,7*1,0*1850*1*1,0)+1,0 = 44 см
Принимаем hтрав
= 44 см
Приближенная проверка траверсы по прочности
Нагрузка на единицу длины опорного листа траверсы
qтрав
= q * Впл
/ 2 = 74,9*48 / 2 = 1770 кг / см
Изгибающий момент и поперечная сила в места приварки к колонне
Мтрав
= 0,5 * qтрав
*а1
2
= 0,5*1770*102
= 88300 кг*см
Qтрав
= qтрав
*а1
= 1770* 10 = 17650 кг
Момент сопротивления сечения листа
Wтрав
= tтрав
* hтрав
2
/ 6 = 1,0*442
/ 6 = 323 см3
Проверка прочности
σ = Мтрав
/ Wтрав
= 88300 / 323 = 273 кг/см2
< Ry
* γc
= 2100*1,0 = 2100 кг/см2
τ = Qтрав
/(hтрав
*tтрав
) = 17650/(44*1,0) = 400 кг/см2
< RS
*γc
= 0,58*Ry
*γc
= 0,58*2100*1,0 = 1218кг/см2
σпр
= √σ2
+ 3 * τ2
= √ 2732
+ 3*4002
= 742 кг/см2
< Ry
* γc
= 2100*1,0 = 2100 кг/см2
→ прочность траверсы обеспечена.
7
.4.3.
Расчет дополнительного ребра.
Принимаем толщину ребра tр
= 1,0см
Np
= q* bк
/ 2 * hк
=74,9 * 42/2 *36= 57200кг.
Принимаем высоту катета Kf
= 1,0 см
Из условия прочности швов:
hк
тр
= Np
/4* βf
* Kf
* Rwf
* γc
* γwf
)= 57200 / (4*0,7*1,0*1850*1,0*1,0)=11,05 см
Из условий прочности ребра на срез: hр
тр
= Np
/2* tp
* Rs
= 57200/2*1,0*1360 = 21,1 см
Принимаем hр
= 22см >hр
тр
= 21,1см. Во избежании выпучивания hр
/ tp
= 22,0/1,0 = 22<30,
lр
/ tp
= hк
/ tp
= 36/1,0 = 36 < 50.
Принятая конструкция базы
7.5 Расчет оголовка
Конструктивно принимаем t'пл
= 2,0 см и Kf
= 1,0 см.
Высота диафрагмы из условия прочности сварных швов
hд
тр
= N / (4 * βf
* Kf
* Rwf
* γc
* γwf
) + 1,0 = 232*103
/(4*0,7*1,0*1850*1*1,0) + 1,0 = 44 см
Принимаем hд
= 44 см
Требуемая толщина диафрагмы из условия прочности торца на смятие
tд.см
тр
= N / ((bf
' + 2 * tпл
' ) * Rp
) = 232*103
/ ((25 +2*2,0)*3510) = 2,4 см
Требуемая толщина диафрагмы из условия прочности на срез
tд.ср
тр
= N / (2 * hд
* RS
) = 232*103
/ ((2*50*1360) = 1,96 см
Принимаем tд
= 2,4 см > tд.ср
тр
= 1,96 см
Толщина планок, к которым крепится диафрагма
tпл
≥ 0,5 tд
= 0,5*2,4 = 12 мм
Принимаем tпл
= 1,2 см.
Принятая конструкция оголовка
Список литературы
:
1. СНиП П-23-81. Стальные конструкции. Нормы проектирования. М.: Стройиздат, 1982. 96 с.
2. СНиП П-6-74. Нагрузки воздействия. Госстой СССР. М.: Стройиздат, 1976. 54 с.
3. Металлические конструкции: Учебник для вузов / Под ред. Е.И. Беленя. – 6-е изд., перераб./ М.: Стройиздат, 1985. 560стр.
4. Михайлов А.М. Сварные конструкции. И., Стройиздат, 1983. 367 с.
5. Лапшин Б.С. К расчету балок в упругопластической стадии по СНиП П-23-81. – В кн.: Металлические конструкции и испытания сооружений: межвуз. темат. сб. тр. Л.: ЛИСИ, 1984, с. 68-75.
|