| Московский городской институт управления Правительства Москвы
Лабораторные работы
по дисциплине
«Экономико-математические методы и модели»
Подготовила студентка V курса Евдокимова Е. Д.
Преподаватель – Новикова Г. М.
Москва
2004
Содержание
Задание №1……………………………………………………………….3
Задание №2……………………………………………………………….8
Задание №3……………………………………………………………...11
Задание №4……………………………………………………………...14
Задание №5……………………………………………………………...16
Задание №6……………………………………………………………...20
Задание №1
Тема: Сетевое моделирование при планировании
Задача: Разработка, анализ и оптимизация сетевого графика при календарном планировании проекта
Компания «АВС» реализует проекты серийного производства различных видов продукции. Каждый проект обеспечивает получение в неделю 100 тыс. $ дополнительной прибыли. Перечень работ и их характеристики представлены в таблице 1.1.
Таблица 1.1
Перечень работ и их характеристики
| Работы
|
Непосредственно предшествующие работы
|
Продолжительность работы, недель
|
Стоимость работы, тыс. $ при t(i,j)=tHB
(I,j)
|
Коэффициент затрат на ускорение работы
|
| tmin
|
tmax
|
| A
|
-
|
4
|
6
|
110
|
22
|
| B
|
-
|
7
|
9
|
130
|
28
|
| C
|
-
|
8
|
11
|
160
|
18
|
| D
|
A
|
9
|
12
|
190
|
35
|
| E
|
C
|
5
|
8
|
150
|
28
|
| F
|
B, E
|
4
|
6
|
130
|
25
|
| G
|
C
|
11
|
15
|
260
|
55
|
| H
|
F, G
|
4
|
6
|
90
|
15
|
Задание:
1. Изобразить проект с помощью сетевой модели.
2. Определить наиболее вероятную продолжительность каждой работы.
3. Найти все полные пути сетевого графика, определить критический путь, ожидаемую продолжительность выполнения проекта и полную стоимость всех работ.
4. Разработать математическую модель оптимизации процесса реализации проекта.
Сетевой график
   D D
A H
     B F B F
 C E C E
G
Наиболее вероятная продолжительность работ
tНВ
= (2tmin
+ 3tmax
)/5
tНВ
A
= (2*4 + 3*6)/5 = 5,2
tНВ
B
= (2*7 + 3*9)/5 = 8,2
tНВ
C
= (2*8 + 3*11)/5 = 9,8
tНВ
D
= (2*9 + 3*12)/5 = 10,8
tНВ
E
= (2*5 + 3*8)/5 = 6,8
tНВ
F
= (2*4 + 3*6)/5 = 5,2
tНВ
G
= (2*11 + 3*15)/5 = 13,4
tНВ
H
= (2*4 + 3*6)/5 = 5,2
Возможные полные пути
I. 1 – 2 – 5. Длина: tНВ
A
+ tНВ
D
=5,2 + 10,8 = 16
II. 1 – 3 – 6 – 5. Длина: tНВ
B
+ tНВ
F
+ tНВ
H
= 8,2 + 5,2 +5,2 = 18,6
III. 1 – 4 – 6 – 5. Длина: tНВ
C
+ tНВ
G
+ tНВ
H
= 9,8 + 13,4 + 5,2 = 28,4
IV. 1 – 4 – 3 – 6 – 5. Длина: tНВ
C
+ tНВ
E
+ tНВ
F
+ tНВ
H
= 9,8 + 6,8 + 5,2 + 5,2= = 27
Максимальная длина пути, равная 28,4 недели соответствует пути III, на котором лежат работы C, G, H. Следовательно, он является критическим.
Математическая модель
Примем за x1,
x2
, …, x8
продолжительность работ A, B,…, H соответственно.
x1
³ 4 (1)
Реклама

x2
³ 7 (2)
x3
³ 8 (3)
x4
³ 9 (4)
x5
³ 5 (5)
x6
³ 4 (6)
x7
³ 11 (7)
x8
³ 4 (8)
x1
£ 6 (9)
x2
£ 9 (10)
x3
£ 11 (11)
x4
£ 12 (12)
x5
£ 8 (13)
x6
£ 6 (14)
x7
£ 15 (15)
x8
£ 6 (16)
x1
+ x4
+ x9
£ 28,4 (17)
x2
+ x6
+ x8
+ x9
£ 28,4 (18)
x3
+ x7
+ x8
+ x9
£ 28,4 (19)
x3
+ x5
+ x6
+ x8
+ x9
£ 28,4 (20)
 Функция цели: 22x1
+ 28x2
+ 18x3
+ 35x4
+ 28x5
+ 25x6
+ 55x7
+ 15x8
+ 100x9
max Функция цели: 22x1
+ 28x2
+ 18x3
+ 35x4
+ 28x5
+ 25x6
+ 55x7
+ 15x8
+ 100x9
max
Исходная матрица
Таблица 1.2
| №
|
x1
|
x2
|
x3
|
x4
|
x5
|
x6
|
x7
|
x8
|
x9
|
Знак
|
Св. чл.
|
| 1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
³
|
4
|
| 2
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
³
|
7
|
| 3
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
³
|
8
|
| 4
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
³
|
9
|
| 5
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
³
|
5
|
| 6
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
³
|
4
|
| 7
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
³
|
11
|
| 8
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
³
|
4
|
| 9
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
£
|
6
|
| 10
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
£
|
9
|
| 11
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
£
|
11
|
| 12
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
£
|
12
|
| 13
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
£
|
8
|
| 14
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
£
|
6
|
| 15
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
£
|
15
|
| 16
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
£
|
6
|
| 17
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
£
|
28,4
|
| 18
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
£
|
28,4
|
| 19
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
£
|
28,4
|
| 20
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
£
|
28,4
|
| Ф. ц.
|
22
|
28
|
18
|
35
|
28
|
25
|
55
|
15
|
100
|
max
|
Решение
x1
= 6
x2
= 9
x3
= 8
x4
= 12
x5
= 7
x6
= 4
x7
= 11
x8
= 4
x9
= 5,4
Т. к. x9
= 5,4, то длина критического пути уменьшится на эту величину. Проверим это утверждение:
x3
+ x7
+ x8
= 8 + 11 + 4 = 23
Уменьшение времени выполнения работы, как правило, связано с увеличением затрат. В таблице 1.3 определим прирост затрат при уменьшении времени реализации проекта.
Таблица 1.3
Изменение затрат при уменьшении времени реализации проекта
| Работа
|
х
|
tHB
|
D x
|
Куск
|
D затрат
|
Стоимость
|
Итого затрат
|
| A
|
6
|
5,2
|
-0,8
|
22
|
-17,6
|
110
|
92,4
|
| B
|
9
|
8,2
|
-0,8
|
28
|
-22,4
|
130
|
107,6
|
| C
|
8
|
9,8
|
1,8
|
18
|
32,4
|
160
|
192,4
|
| D
|
12
|
10,8
|
-1,2
|
35
|
-42
|
190
|
148
|
| E
|
7
|
6,8
|
-0,2
|
28
|
-5,6
|
150
|
144,4
|
| F
|
4
|
5,2
|
1,2
|
25
|
30
|
130
|
160
|
| G
|
11
|
13,4
|
2,4
|
55
|
132
|
260
|
392
|
| H
|
4
|
5,2
|
1,2
|
15
|
18
|
90
|
108
|
| Всего затрат
|
124,8
|
1220
|
1344,8
|
Таким образом, время выполнения работ A, B, D, E увеличилось по сравнению с наиболее вероятным; продолжительность остальных работ уменьшилась. Затраты на реализацию проекта возросли на 124,8 тыс. $. Увеличение затрат произошло, в основном, из-за работы G, по которой наблюдается наибольшее сокращение времени в сочетании с наивысшим коэффициентом затрат на выполнение работы.
Из-за сокращения критического пути проект будет введен в эксплуатацию на 5,4 недели раньше. Т. к. прибыль за неделю составляет 100 тыс. $, то за этот срок она составит 100 тыс. $ * 5,4 = 540 тыс. $.
В результате дополнительная прибыль с учетом возрастания затрат на проведение работ составит 540 тыс. $ - 124,8 тыс. $ = 415,2 тыс. $
Задание №2
Тема: Графы
Реклама

Задача о коммивояжере
Имеется 4 пункта. Время переезда из пункта I в пункт j представлено в таблице 2.1.
Таблица 2.1
Исходные данные
| Из пункта i
|
В пункт j
|
| 1
|
2
|
3
|
4
|
| 1
|
0
|
8
|
8
|
6
|
| 2
|
4
|
0
|
6
|
12
|
| 3
|
10
|
12
|
0
|
18
|
| 4
|
8
|
10
|
4
|
0
|
График представлен на рисунке.
Требуется найти оптимальный маршрут, вычеркнув из таблицы отсутствующие маршруты.
Математическая модель
Обозначим за x маршруты, приведенные в таблице 2.2.
Таблица 2.2
Обозначения
| xi
|
Пункт отправления
|
Пункт назначения
|
Время переезда
|
| x1
|
1
|
2
|
8
|
| x2
|
1
|
3
|
8
|
Продолжение
|
| x3
|
1
|
4
|
6
|
| x4
|
2
|
1
|
4
|
| x5
|
2
|
3
|
6
|
| x6
|
2
|
4
|
12
|
| x7
|
3
|
1
|
10
|
| x8
|
3
|
2
|
12
|
| x9
|
3
|
4
|
18
|
| x10
|
4
|
1
|
8
|
| x11
|
4
|
2
|
10
|
| x12
|
4
|
3
|
4
|
Сумма входящих и исходящих маршрутов в каждом пункте равна 1. Следовательно, система условий-ограничений выглядит следующим образом:
x1
+ x2
+ x3
= 1 (1)
x4
+ x5
+ x6
= 1 (2)
x7
+ x8
+ x9
= 1 (3)
x10
+ x11
+ x12
= 1 (4)
x4
+ x7
+ x10
= 1 (5)
x1
+ x8
+ x11
= 1 (6)
x2
+ x5
+ x12
= 1 (7)
x3
+ x6
+ x9
= 1 (8)
 Функция цели: 8x1
+ 8x2
+ 6x3
+ 4x4
+ 6x5
+ 12x6
+ 10x7
+ 12x8
+ 18x9
+ 8x10
+ 10x11
+ 4x12
min Функция цели: 8x1
+ 8x2
+ 6x3
+ 4x4
+ 6x5
+ 12x6
+ 10x7
+ 12x8
+ 18x9
+ 8x10
+ 10x11
+ 4x12
min
Исходная матрица условий задачи представлена в таблице 2.3.
Таблица 2.3
| №
|
x1
|
x2
|
x3
|
x4
|
x5
|
x6
|
x7
|
x8
|
x9
|
х10
|
x11
|
x12
|
Св.чл.
|
Зн
|
| 1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
=
|
| 2
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
=
|
| 3
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
=
|
| 4
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
=
|
| 5
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
1
|
=
|
| 6
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
=
|
| 7
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
=
|
| 8
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
=
|
| Фц.
|
8
|
8
|
6
|
4
|
6
|
12
|
10
|
12
|
18
|
8
|
10
|
4
|
min
|
Исходная матрица
Решение
x3
= 1
x5
= 1
x7
= 1
x8
= 0
x11
= 1
    Это означает, что на графике остаются только пути, соответствующие переменным х3
, х5
, х7
, х11
(1 4, 2 3, 3 1, 4 2). Функционал равен 12, т. е. время пути будет равно 12 единицам. График при этом выглядит следующим образом. Это означает, что на графике остаются только пути, соответствующие переменным х3
, х5
, х7
, х11
(1 4, 2 3, 3 1, 4 2). Функционал равен 12, т. е. время пути будет равно 12 единицам. График при этом выглядит следующим образом.
Задание №3
Тема: Графы
Задача о максимальном потоке
Имеется трубопроводная сеть с заданной Sij
пропускной способностью каждого участка из i-го узла в j-й узел и мощностью насосной станции, расположенной в узле. Необходимо рассчитать максимальную пропускную способность сети из начального узла в конечный узел.
a    исток
a исток
a    сток сток

Пропускная способность Sij
, тыс. тонн
S12
= 4
S13
= 7
S14
= 8
S23
= 3
S25
= 5
S34
= 8
S35
= 9
S45
= 9
Математическая модель
Обозначим за х1, 2, …, 8
перевозки по маршрутам 12, 13, 14, 23, 25, 34, 35, 45 соответственно, а за х9
– пропускную способность конечного узла сети.
Сумма входящих в каждый узел потоков равна сумме выходящих, причем интенсивность каждого потока не может превышать пропускную способность своего участка сети. Поэтому система условий-ограничений выглядит следующим образом.
х9
- х1
– х2
– х3
= 0 (1)
х1
– х4
– х5
= 0 (2)
х2
+ х4
– х6
– х7
= 0 (3)
х3
+ х6
– х8
= 0 (4)
х5
+ х7
+ х8
– х9
= 0 (5)
х1
£ 4 (6)
х2
£ 7 (7)
х3
£ 8 (8)
х4
£ 3 (9)
х5
£ 5 (10)
х6
£ 8 (11)
х7
£ 9 (12)
х8
£ 9 (13)
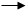 Функция цели: х9
max Функция цели: х9
max
Таблица 3.1
Исходная матрица
| №
|
х1
|
х2
|
х3
|
х4
|
х5
|
х6
|
х7
|
х8
|
х9
|
Знак
|
Св.чл.
|
| 1
|
-1
|
-1
|
-1
|
0
|
0
|
0
|
0
|
0
|
1
|
=
|
0
|
| 2
|
1
|
0
|
0
|
-1
|
-1
|
0
|
0
|
0
|
0
|
=
|
0
|
| 3
|
0
|
1
|
0
|
1
|
0
|
-1
|
-1
|
0
|
0
|
=
|
0
|
| 4
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
-1
|
0
|
=
|
0
|
| 5
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
-1
|
=
|
0
|
| 6
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
£
|
4
|
| 7
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
£
|
7
|
| 8
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
£
|
8
|
| 9
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
£
|
3
|
| 10
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
£
|
5
|
| 11
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
£
|
8
|
| 12
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
£
|
9
|
| 13
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
£
|
9
|
| Ф. ц.
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
max
|
Решение
х1
= 4
х2
= 7
х3
= 8
х5
= 4
х7
= 7
х8
= 8
х9
= 19
Функционал в данной задаче равен –481, что не имеет смысла при заданных условиях. Однако, исходя из математической модели, функционал в данной задаче равен значению х9
. Таким образом, максимальная пропускная способность сети составит 19 тыс. тонн. При этом некоторые маршруты окажутся незадействованными (х4
и х6
). График будет выглядеть следующим образом.
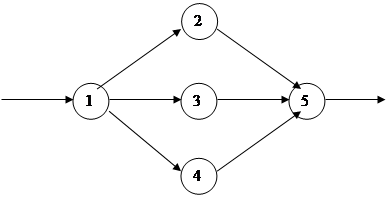
Задание №4
Тема: Системы массового обслуживания
Задача: Рационализация функционирования системы управления аэропортом на базе анализа марковских процессов
Различные аэропорты имеют отделы системы управления, функциональная связь которых и интенсивность потоков информации представлены на рисунке и в таблице 4.1.
Требуется вычислить вероятности состояний в стационарном режиме по значениям интенсивности перехода.
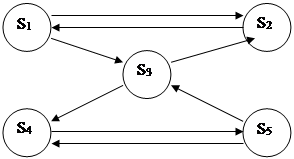
Таблица 4.1
Исходные данные
| Интенсивность потоков (переходов)
|
| l12
|
l13
|
l21
|
l32
|
l34
|
l45
|
l53
|
l54
|
| 3
|
2
|
1
|
3
|
2
|
2
|
3
|
1
|
Математическая модель
Примем за х1
, х2
, …, х5
предельные вероятности состояний в стационарном режиме пунктов S1
, S2
, …, S5
соответственно. Произведение вероятности состояния на интенсивность исходящих из этого пункта потоков равна произведению интенсивностей входящих потоков на вероятность состояния в стационарном режиме пунктов их отправления. Система уравнений Колмогорова для данной задачи в общем виде выглядит следующим образом:
(l13
+ l12
)* х1
= l21
* х2
(1)
l21
* х2
= l12
* х1
+ l32
* х3
(2)
(l32
+ l34
)* х3
= l13
* х1
+ l53
* х5
(3)
l45
* х4
= l34
* х3
+ l54
* х5
(4)
(l54
+ l53
)* х5
= l45
* х4
(5)
Кроме того, сумма всех вероятностей равна 1. При подстановке данных таблицы 4.1 и добавлении переменной х6
получаем:
5 х1
- х2
+ х6
= 0 (1)
х2
- 3х1
- 3х3
+ х6
= 0 (2)
5 х3
- 2х1
- 3х5
+ х6
= 0 (3)
2 х4
- 2х3
– х3
+ х6
= 0 (4)
4 х5
- 2х4
+ х6
= 0 (5)
х1
+ х2
+ х3
+ х4
+ х5
+ х6
= 1 (6)
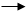 Функция цели: М х6
max Функция цели: М х6
max
Таблица 4.2.
Исходная матрица
| №
|
х1
|
х2
|
х3
|
х4
|
х5
|
х6
|
Св.чл.
|
Знак
|
| 1
|
5
|
-1
|
0
|
0
|
0
|
1
|
0
|
=
|
| 2
|
-3
|
1
|
-3
|
0
|
0
|
1
|
0
|
=
|
| 3
|
-2
|
0
|
5
|
0
|
-3
|
1
|
0
|
=
|
| 4
|
0
|
0
|
-2
|
2
|
-1
|
1
|
0
|
=
|
| 5
|
0
|
0
|
0
|
-2
|
4
|
1
|
0
|
=
|
| 6
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
=
|
| Ф.ц.
|
0
|
0
|
0
|
0
|
0
|
М
|
max
|
Решение
Функционал = -500
х1
= 0,125
х2
= 0,625
х3
= 0,083
х4
= 0,111
х5
= 0,055
Сумма данных вероятностей составляет 0,999, т. е. погрешность, полученная при расчетах, крайне незначительна.
Задание №5
Тема: Имитационное моделирование
Задача: Расчет и анализ графика запуска-выпуска продукции в цехе мелкосерийного производства
В таблице 5.1 представлены технологические маршруты изготовления различных видов продукции, а также директивное время исполнения заказов (в условных единицах) и нормы затрат времени на обработку одной партии продукции на каждом из типов оборудования.
Общая масса заказа по каждому виду продукции разбивается на N партий так, что для каждого вида продукции выполняется условие:
Общая масса заказа = (масса партий)*(число партий)
Нормы затрат времени в каждом эксперименте имитационного моделирования обратно пропорциональны числу партий.
Требуется определить оптимальный маршрут изготовления продукции.
Таблица 5.1
Технологические маршруты изготовления продукции
| Продукция
Оборудование
|
Эксперимент №1
|
Эксперимент №2
|
Эксперимент №3
|
| 1
|
2
|
3
|
4
|
5
|
6
|
1
|
2
|
3
|
4
|
5
|
6
|
1
|
2
|
3
|
4
|
5
|
6
|
| 1
|
1
|
1
|
1
|
1
|
1
|
1
|
2
|
2
|
2
|
2
|
2
|
2
|
4
|
4
|
4
|
4
|
4
|
4
|
| 2
|
6
|
-
|
-
|
-
|
-
|
-
|
12
|
-
|
-
|
-
|
-
|
-
|
24
|
-
|
-
|
-
|
-
|
-
|
| 3
|
-
|
-
|
6
|
-
|
-
|
-
|
-
|
-
|
12
|
-
|
-
|
-
|
-
|
-
|
24
|
-
|
-
|
-
|
| 4
|
-
|
-
|
-
|
-
|
3
|
-
|
-
|
-
|
-
|
-
|
6
|
-
|
-
|
-
|
-
|
-
|
12
|
-
|
| 5
|
-
|
-
|
-
|
-
|
-
|
2
|
-
|
-
|
-
|
-
|
-
|
4
|
-
|
-
|
-
|
-
|
-
|
8
|
| 6
|
1
|
2
|
-
|
2
|
-
|
-
|
2
|
4
|
-
|
6
|
-
|
-
|
4
|
8
|
-
|
12
|
-
|
-
|
| Количество партий
|
4
|
4
|
4
|
4
|
4
|
4
|
2
|
2
|
2
|
2
|
2
|
2
|
1
|
1
|
1
|
1
|
1
|
1
|
Тд
= 27
Решение
В результате применения программы «APOSUM» было получено 3 варианта решения. Время изготовления заказа в каждом из них составляет соответственно 41, 48 и 52 единицы. Ближе всего к нормативному времени находится вариант 1. Количество переналадок при этом равно 19, что больше, чем в других вариантах (10 и 5), однако решающее значение имеет время. Изменяя длительность обработки изделий, можно уменьшить время с 41 до 29 единиц. Измененная длительность обработки изделий представлена в таблице 5.2.
Таблица 5.2.
Длительность обработки изделий
| Ст. 1
|
Ст. 2
|
Ст. 3
|
Ст. 4
|
Ст. 5
|
Ст. 6
|
Объем заказа
|
Длит. обраб.
|
| Изделие 1
|
1
|
6
|
0
|
0
|
0
|
1
|
4
|
26
|
| Изделие 2
|
1
|
0
|
0
|
0
|
0
|
2
|
4
|
14
|
| Изделие 3
|
1
|
0
|
6
|
0
|
0
|
0
|
4
|
25
|
| Изделие 4
|
1
|
0
|
0
|
0
|
0
|
3
|
4
|
12
|
| Изделие 5
|
1
|
0
|
0
|
3
|
0
|
0
|
4
|
25
|
| Изделие 6
|
1
|
0
|
0
|
0
|
2
|
0
|
4
|
24
|
В итоге получился следующий график запуска-выпуска продукции.
Таблица 5.3.
График запуска-выпуска продукции
| № п/п
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
| Продукция
|
4
|
1
|
4
|
3
|
4
|
2
|
1
|
3
|
2
|
4
|
2
|
| Время запуска
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
| Время выпуска
|
4
|
9
|
12
|
10
|
15
|
17
|
18
|
16
|
20
|
23
|
25
|
| Длительность обработки
|
4
|
8
|
10
|
7
|
11
|
12
|
12
|
9
|
12
|
14
|
15
|
| Пролеживание
|
0
|
0
|
6
|
0
|
7
|
9
|
4
|
2
|
9
|
10
|
12
|
Продолжение
| № п/п
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
21
|
22
|
23
|
24
|
| Продукция
|
2
|
1
|
3
|
5
|
5
|
6
|
6
|
1
|
3
|
5
|
6
|
6
|
5
|
| Время запуска
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
21
|
22
|
23
|
| Время выпуска
|
27
|
28
|
22
|
18
|
21
|
19
|
21
|
29
|
28
|
24
|
24
|
26
|
27
|
| Длительность обработки
|
16
|
16
|
9
|
4
|
6
|
3
|
4
|
11
|
9
|
4
|
3
|
4
|
4
|
| Пролеживание
|
13
|
8
|
2
|
0
|
2
|
0
|
1
|
3
|
2
|
0
|
0
|
1
|
0
|
Время и очередность запуска и выпуска каждой партии продукции, последовательность и время использования каждого оборудования проиллюстрированы далее графиком Ганта.
График Ганта
Задание №6
Тема: Матричные модели балансового метода планирования
Задача: Разработка межпродуктового баланса производства и распределения продукции предприятия
В трех цехах приборостроительного завода изготовляются датчики, приборы и их узлы, основная часть которых идет на внутреннее потребление при сборке блоков АСУ, остальная является конечным продуктом и поставляется внешним приборостроительным и машиностроительным организациям, а также в ремонтные мастерские.
Требуется составить межпродуктовый баланс производства и распределения продукции, если известны коэффициенты прямых затрат и конечный продукт (таблица 6.1).
Таблица 6.1.
Исходные данные
| Производящие цехи
|
Потребляющие цехи (коэф. прямых затрат)
|
Конечная продукция
|
| №1
|
№2
|
№3
|
| №1
|
0,15
|
0,10
|
0,30
|
100
|
| №2
|
0,25
|
0,15
|
0,25
|
280
|
| №3
|
0,30
|
0,25
|
0
|
320
|
Математическая модель
х1
= 0,15х1
+ 0,1х2
+ 0,3х3
+ 100
х2
= 0,25х1
+ 0,15х2
+ 0,25х3
+ 280
х3
= 0,3х1
+ 0,25х2
+ 0х3
+ 320
Отсюда, умножив уравнения на –1, получаем следующую систему уравнений ограничений:
0,85х1
- 0,1х2
- 0,3х3
- х4
= 100 (1)
-0,25х1
+ 0,85х2
- 0,25х3
- х4
= 280 (2)
-0,3х1
+ 0,25х2
+ х3
- х4
= +320 (3)
 Функция цели: -Мх4
max Функция цели: -Мх4
max
Исходная матрица условий задачи представлена в таблице 6.2.
Таблица 6.2.
Исходная матрица
| №
|
х1
|
х2
|
х3
|
х4
|
Знак
|
Св. чл.
|
| 1
|
0,85
|
-0,1
|
-0,3
|
-1
|
=
|
100
|
| 2
|
-0,25
|
0,85
|
-0,25
|
-1
|
=
|
280
|
| 3
|
-0,3
|
-0,25
|
1
|
-1
|
=
|
320
|
| Ф. ц.
|
0
|
0
|
0
|
-М
|
max
|
Решение
Функционал = 0
х1
= 401,292
х2
= 622,756
х3
= 596,077
Умножив полученные значения валового продукта на коэффициенты прямых затрат, получим решение, представленное в таблице 6.3.
Таблица 6.3.
Решение
| Производящие цехи
|
Потребляющие цехи
|
Конечный продукт
|
Валовой продукт
|
| 1
|
2
|
3
|
| 1
|
60,15
|
40,1
|
120,3
|
100
|
401
|
| 2
|
155,75
|
93,45
|
155,75
|
280
|
623
|
| 3
|
178,8
|
149,0
|
0
|
320
|
596
|
| Итого
|
В таблице показаны затраты на производство продукции в количественном выражении.
|