| Содержание
Введение…………………………………………………………………………5
1. Основные понятия сетевого планирования и управления…………….…..7
1.1 Основные параметры сетевой модели системы планирования и управления………………………………………………………………….7
1.2 Правила построения сетевых графиков. Характеристики элементов сетевой модели…………………………………………………………......9
2. Методы сетевого планирования…………………………………………..15
2.1 Метод критического пути………………………………………………..15
2.2 Метод оценки и пересмотра планов (ПЕРТ, PERT)……………………..17
2.3 Метод графической оценки и анализа (GERT)…………………………..19
3. Численная реализация задачи сетевого планирования…………………...20
Заключение…………………………………………………………………......26
Список использованной литературы………………………………………….28
Введение
Сетевое планирование и управление (СПУ), система планирования и управления разработкой крупных народно-хозяйственных комплексов, научными исследованиями, конструкторской и технологической подготовкой производства новых видов изделий, строительством и реконструкцией, капитальным ремонтом основных фондов путём применения сетевых графиков. Система СПУ позволяет устанавливать взаимосвязь планируемых работ и получаемых результатов, более точно рассчитывать план, а также своевременно осуществлять его корректировку.
Первоначальные идеи СПУ были разработаны в конце 50-х годов в США и реализованы в виде двух систем сетевого анализа – PERT (Program Evaluation and Review Technique – оценка программ и способов проверки) и CPM (Critical Path Method – метод критического пути).
В России работы по сетевому планированию начались в 60-х годах. Тогда методы СПУ нашли применение в строительстве и научных разработках. В дальнейшем сетевые методы стали широко применяться и в других областях народного хозяйства.
Актуальность выбранной темы обусловлена постоянной работой внутри производственно-хозяйственной системы по ее совершенствованию, для чего необходимо планировать производственный процесс в целом, рассматривая работы во взаимосвязи.
Применение системы сетевого планирования способствует разработке оптимального варианта стратегического плана развития предприятия, который служит основой оперативного управления комплексом работ в ходе его осуществления. Основным плановым документом в этой системе является сетевой график, или просто сеть, представляющий информационно-динамическую модель, в которой отражаются все логические взаимосвязи и результаты выполняемых работ, необходимых для достижения конечной цели стратегического планирования. В сетевом графике с необходимой степенью детализации изображается, какие работы, в какой последовательности и за какое время предстоит выполнить, чтобы обеспечить окончание всех видов деятельности не позже заданного или планируемого периода.
Реклама

При сетевом планировании производства:
- видна цепочка работ, от которых зависит своевременное выполнение проекта,
- есть простые математические зависимости, позволяющие делать расчёты,
- после составления сетевого графика выявляются резервы, которые можно использовать внутри проекта и, следовательно, сократить длительность и стоимость.
Каким бы совершенным ни был производственный процесс, на предприятии всегда найдутся внутрипроизводственные резервы. С течением времени в силу появления новых достижений научно-технического прогресса величина этих резервов будет возрастать.
Методы сетевого моделирования относятся к методам принятия оптимальных решений, что оправдывает рассмотрение этого типа моделей в данной курсовой работе.
1.Основные понятия сетевого планирования и управления.
1.1
Основные параметры сетевой модели системы планирования и управления.
Математический аппарат сетевых моделей базируется на теории графов.
Графом называется совокупность двух конечных множеств:
- множества точек, которые называются вершинами, и множества пар вершин, которые называются ребрами. Если рассматриваемые пары вершин являются упорядоченными, т. е. на каждом ребре задается направление, то граф называется ориентированным; в противном случае — неориентированным. Последовательность неповторяющихся ребер, ведущая от некоторой вершины к другой, образует путь.
Граф называется связным, если для любых двух его вершин существует путь, их соединяющий; в противном случае граф называется несвязным.
В экономике чаще всего используются два вида графов: дерево и сеть.
Дерево представляет собой связный граф без циклов, имеющий исходную вершину (корень) и крайние вершины; пути от исходной вершины к крайним вершинам называются ветвями.
Сеть — это ориентированный конечный связный граф, имеющий начальную вершину (источник) и конечную вершину (сток). Таким образом, сетевая модель представляет собой граф вида «сеть».
Реклама

В экономических исследованиях сетевые модели возникают при моделировании экономических процессов методами сетевого планирования и управления (СПУ).
Объектом управления в системах сетевого планирования и управления являются коллективы исполнителей, располагающих определенными ресурсами и выполняющих определенный комплекс операций, который призван обеспечить достижение намеченной цели, например, разработку нового изделия, строительства объекта и т.п.
Основой сетевого планирования и управления является сетевая модель (СМ), в которой моделируется совокупность взаимосвязанных работ и событий, отображающих процесс достижения определенной цели. Она может быть представлена в виде графика или таблицы.
Основные понятия сетевой модели:
1) событие;
2) работа;
3) путь.
Работа характеризует материальное действие, требующее использования ресурсов, или логическое, требующее лишь взаимосвязи событий. При графическом представлении работа изображается стрелкой, которая соединяет два события. Она обозначается парой заключенных в скобки чисел (i,j
), где i
— номер события, из которого работа выходит, а j — номер события, в которое она входит. Работа не может начаться раньше, чем свершится событие, из которого она выходит. Каждая работа имеет определенную продолжительность t
(i,j
)-Например, запись t (2,5) = 4 означает, что работа (2,5) имеет продолжительность 5 единиц.
На рис. 1 графически представлена сетевая модель, состоящая из 11 событий и 16 работ, продолжительность выполнения которых указана над работами.
«Рисунок 1 – Пример сетевой модели».
Событиями называются результаты выполнения одной или нескольких работ. Они не имеют протяженности во времени. Событие свершается в тот момент, когда оканчивается последняя из работ, входящая в него. События обозначаются одним числом и при графическом представлении сетевая модель изображаются кружком (или иной геометрической фигурой), внутри которого проставляется его порядковый номер (i = 1, 2, ..., n).
В сетевой модели имеется начальное событие (с номером 1), из которого работы только выходят, и конечное событие (с номером N), в которое работы только входят.
Путь — это цепочка следующих друг за другом работ, соединяющих начальную и конечную вершины, например, в приведенной выше модели путями являются L1
= (1, 2, 3, 7, 10, 11), L2
= (1, 2, 4, 6, 11) и др.
Продолжительность пути определяется суммой продолжительностей составляющих его работ. Путь, имеющий максимальную длину, называют критическим и обозначают LKp
, а его продолжительность — tкр. Работы, принадлежащие критическому пути, называются критическими. Их несвоевременное выполнение ведет к срыву сроков всего комплекса работ.
Сетевая модель имеют ряд характеристик, которые позволяют определить степень напряженности выполнения отдельных работ, а также всего их комплекса и принять решение о перераспределении ресурсов.
1.2
Правила построения сетевых графиков. Характеристики элементов сетевой модели.
При построении сетевых графиков необходимо соблюдать следующие правила:
1) в сети не должно быть тупиков, то есть событий, из которых не выходит ни одной работы, если только эти события не являются для данной сети завершающими.
Наличие тупиков в сети, как правило, указывает на то, что либо связь отсутствует ошибочно, либо результат работы или работ, непосредственно предшествующих этому событию, никому из исполнителей данного комплекса операций не нужен. Следовательно, такие работы являются лишними и могут быть аннулированы.
2) в сети не должно быть событий, в которые не входит ни одной работы, если только эти события не являются для данной сети исходными.
3) в сети не должно быть замкнутых контуров, то есть не должно быть путей, соединяющих некоторое событие с ним же самим.
Наличие замкнутых контуров указывает на случайную или логическую ошибку, допущенную при построении сети. При обнаружении подобной ошибки сеть после соответствующей проверки должна быть исправлена.
4) в сети не должно быть работ, имеющих одинаковые шифры, то есть работ с общими начальным и конечным событиями.
Для любого события i сетевая модель позволяет рассчитать наиболее ранний из возможных сроков его свершения tp(i) и наиболее поздний из допустимых сроков его свершения tп(i) (или для кратности: ранний и поздний сроки свершения события i).
Ранний срок свершения любого события i равен суммарной продолжительности работ, лежащих на максимальном из путей, ведущих к данному событию от исходного события сети, то есть на максимальном из предшествующих событию i путей.
Обозначив максимальный предшествующий событию i путь через L(I-i)max, получим
tp(i)=t[L(I-i)max].
(1)
Поздний срок свершения любого события i, то есть tп(i), равен разности между продолжительностью критического пути и суммарной продолжительностью работ, лежащих на максимальном из путей, ведущих от данного события к завершающему событию сети, то есть на максимальном из следующих за событием i путей.
Обозначим максимальный следующий за событием i путь через L(i-C)max, получим
t
п
(i)=t
кр
-t[L(i-C)max].
(2)
Зная tp(i) и tп(i) для всех событий сети, можно для любой работы (i, j) определить:
1) самый ранний из возможных сроков начала работы (i,j), или, кратко, ранний срок начала tр.н(i,j);
2) самый поздний из допустимых сроков начала работы, или поздний срок начала tп.н(i,j);
3) самый ранний из возможных сроков окончания работы, или ранний срок окончания tр.о(i,j);
4) самый поздний из допустимых сроков окончания работы, или поздний срок окончания tп.о(i,j).
Ранние сроки начала работ определяются ранними сроками свершения их начальных событий, а поздние сроки окончания работ – поздними сроками свершения их конечных событий. Поэтому, зная продолжительность работы t(i,j), указанные выше параметры определить по следующим формулам:
t
р
.
н
(i,j) = tp(i),
(3)
t
п
.
н
(i,j) = t
п
(j) – t(i,j),
(4)
tp.o(i,j) = tp(i) + t(i,j),
(5)
t
п.о(
i
,
j
) =
t
п(
j
).
(6)
Для всех работ критического пути
t
р
.
н
(i,j) = t
п
.
н
(i,j)
и
t
р
.
о
(i,j) = t
п
.
о
(i,j),
(7)
так как начальное и конечное события этих работ находятся на критическом пути, а следовательно,
tp(i) = t
п
(i) = t
п
(j) – t(i,j)
и
t
п
(j) = tp(j) = tp(i) + t(i,j).
(8)
Разница между продолжительностью критического пути и любого другого пути сети t(L) называется полным резервом времени пути и обозначается через P(L):
P
(
L
) =
t
кр –
t
(
L
).
(9)
Величина P(L) показывает, насколько в сумме может быть увеличена продолжительность всех работ, принадлежащих пути L, чтобы при этом не изменилась продолжительность критического пути tкр.
Резерв времени события i обозначается через P(i) и определяется как разница между поздним и ранним сроками свершения данного события, то есть:
P
(
i
) =
t
п(
i
) –
tp
(
i
);
(10)
легко показать, что
P
(
i
) =
P
[
L
(
i
)
max
],
(11)
то есть резерв времени свершения события определяется резервом времени у максимального из путей, проходящих через это событие.
Резерв времени показывает, на какой предельно допустимый период времени можно задержать свершение этого события, не вызывая при этом увеличения tкр.
В системах СПУ используются четыре вида резервов времени работ: полный, свободный, и два вида частных резервов времени.
Полным резервом времени работ (i,j) называется резерв времени, равный величине резерва времени максимального из путей, проходящих через данную работу. Обозначается через Pп(i,j).
Для всех работ критического пути Рп(i,j) = 0.
Величина полного резерва времени может быть определена по следующей формуле:
Рп
(i.j) = t
п
(j) – tp(i) – t(i,j).
(12)
Частные резервы времени образуются в местах пересечения путей различной продолжительности у работ, принадлежащих меньшему пути.
Следует различать два вида частных резервов:
1) частный резерв первого вида P’п(i,j) образуется у работ, непосредственно следующих за событием, в котором пересекаются пути различной продолжительности;
2) частный резерв второго вида P”п(i,j) образуется у работ, непосредственно предшествующих событию, в котором пересекаются пути различной продолжительности.
P’
п
(i,j) =
Рп
(i,j) – P(i),
(13)
P”
п
(i,j) = P
п
(i,j) – P(j).
(14)
Свободным резервом времени работы (i,j) называется та часть ее полного резерва, которая сохраняется у нее при условии, что начальное событие данной работы свершится в самый поздний срок tп(i), а конечное – в самый ранний tp(j):
Pc(i.j) = tp(j) – t
п
(i) – t(i,j).
(15)
Величина свободного резерва времени Pc(i,j) показывает, на какой период времени можно увеличить продолжительность данной работы (i,j), чтобы при этом сохранилась возможность свершения ее конечного события в самый поздний срок.
В ряде систем СПУ напряженность сроков выполнения работ измеряется отношением продолжительностей несовпадающих отрезков максимального пути, проходящего через данную работу, и критического пути. Это отношение называется коэффициентом напряженности работы и обозначается через kн(i.j).
k
н
(i.j) = 1 –
Рп
(i,j) / t”
кр
(i,j)max.
(16)
Другими словами, коэффициент напряженности работы характеризует напряженность сроков ее выполнения с помощью относительной, а не абсолютной величины ее полного резерва времени.
Величина коэффициента напряженности у разных работ в сети лежит в пределах 0 ≤ kн(i,j) ≤ 1, причем у работ критического пути kн(i,j) = 1.
В реальных проектах каждая работа характеризуется не только временем, но и стоимостью выполнения. В этом случае полная стоимость проекта будет равна сумме стоимостей всех входящих в него работ.
2.
Методы сетевого планирования.
2.1 Метод критического пути.
Конечным результатом применения метода критического пути (СРМ) будет построение временного графика выполнения проекта. Для этого проводятся специальные вычисления, в результате чего получаем следующую информацию.
1) общая длительность выполнения проекта;
2) разделение множества процессов, составляющих проект, на критические
и некритические.
Процесс является критическим, если он не имеет "зазора" для времени своего начала и завершения. Таким образом, чтобы весь проект завершился без задержек, необходимо, чтобы все критические процессы начинались и заканчивались в строго определенное время. Для некритического процесса возможен некоторый "дрейф" времени его начала, но в определенных границах, когда время его начала не влияет на длительность выполнения всего проекта.
Для проведения необходимых вычислений определим событие как точку на временной оси, где завершается один процесс и начинается другой. В терминах сети, событие – это сетевой узел. Нам понадобятся также следующие определения и обозначения.
□j
— самое раннее возможное время наступления события j,
∆j
самое позднее возможное время наступления события j,
Dij
— длительность процесса (i, j).
Вычисление критического пути включает два этапа (прохода). При проходе вперед вычисляются самые ранние времена наступления событий, а при проходе назад – самые поздние времена наступления тех же событий.
Проход вперед. Вычисления начинаются в узле 1 и заканчиваются в последнем узле n.
Начальный шаг. Полагаем П1
= 0; это указывает на то, что проект начинается в нулевой момент времени.
– Основной шаг j. Для узла j определяем узлы – р, q, ..., v, непосредственно связанные с узлом j процессами (p,j), {q, j), ..., (v, j), для которых уже вычислены самые ранние времена наступления соответствующих событий. Самое раннее время наступления события j вычисляется по формуле
□
j
=
max(□
P
, +Dpj
, □q
+Dqj
, ..., Uv
+Dv
j
)
(17)
Проход вперед завершается, когда будет вычислена величина Оа для узла п. По определению величина Пу равна самому длинному пути (длительности) от начала проекта до узла (события) у.
Проход назад. В этом проходе вычисления начинаются в последнем узле n и заканчиваются в узле 1.
– Начальный шаг. Полагаем ∆n
= □n
это указывает, что самое раннее и самое позднее времена для завершения проекта совпадают.
– Основной шаг j. Для узла j определяем узлы р, q, ..., v, непосредственно связанные с узлом j процессами (j, р), (j, q), ..., (j, v), для которых уже вычислены самые поздние времена наступления соответствующих событий. Самое позднее время наступления события у вычисляется по формуле:
∆
j
= min(∆
P
- Djp
, ∆
q
- Djq
, ..., ∆
v
-
-
Djv
.)
(18)
Проход назад завершается при вычислении величины ∆1
для узла 1. Процесс (i, j) будет критическим, если выполняются три условия.
1) ∆i
= □i
2) ∆j
= □j
3) ∆j
.-∆i
= □j
- □I
= Dij
Если эти условия не выполняются, то процесс некритический.
Критические процессы должны образовывать непрерывный путь через всю сеть от начального события до конечного.
2.2 Метод оценки и пересмотра планов (ПЕРТ, PERT)
Метод оценки и пересмотра планов PERT представляет собой разновидность анализа по методу критического пути с более критичной оценкой продолжительности каждого этапа проекта. При использовании этого метода необходимо оценить наименьшую возможную продолжительность выполнения каждой работы, наиболее вероятную продолжительность и наибольшую продолжительность на тот случай, если продолжительность выполнения этой работы будет больше ожидаемой. Метод ПЕРТ допускает неопределенность продолжительности операций и анализирует влияние этой неопределенности на продолжительность работ по проекту в целом.
Этот метод используется, когда для операции сложно задать и определить точную длительность.
Особенность метода PERT заключается в возможности учета вероятностного характера продолжительностей всех или некоторых работ при расчете параметров времени на сетевой модели. Он позволяет определять вероятности окончания проекта в заданные периоды времени и к заданным срокам.
Метод PERT отличается от СРМ тем, что здесь длительность процессов характеризуется тремя оценками.
1) оптимистичная оценка времени а, когда предполагается, что выполнение
процесса будет происходить максимально быстро.
2) наиболее вероятная оценка времени m, когда предполагается, что выполнение процесса будет происходить нормально.
3) пессимистическая оценка времени b, когда предполагается, что выполнение процесса будет происходить очень медленно.
Любая возможная оценка времени выполнения процесса будет лежать в интервале (а, b). Поэтому оценка времени m также должна лежать в этом интервале. На основе этих оценок среднее время D выполнения процесса и дисперсия v вычисляются пo формулам
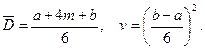 (19)
(19)
Вычисления метода СРМ, выполнимы, если заменить значения длительностей D процессов оценками 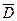 . .
Теперь можно определить вероятность того, что узел j модели будет достигнут в заранее запланированное время Sj
Пусть ej
— время наискорейшего достижения узла j. Поскольку длительности выполнения процессов, которые ведут от начального узла к узлу j, — случайные величины, то ej
также является случайной величиной. Предположив, что все процессы в сети статистически независимы, можно определить среднее (математическое ожидание) М{еj
} и дисперсию var{ej
} следующим образом. Если существует только один путь от начального узла к узлу j, то среднее является суммой ожидаемых длительностей D выполнения всех процессов, входящих в этот путь, а дисперсия равна сумме дисперсий v тех же процессов. С другой стороны, если к узлу j ведет более одного пути, то до того, как будут вычислены среднее и дисперсия, необходимо найти вероятностное распределение длительности выполнения процессов, которые составляют самый длинный путь. Эта задача достаточно сложная, поскольку она эквивалентна задаче, вычисляющей распределение ""максимума нескольких случайных величин. Для упрощения этой задачи среднее М{ej
} и дисперсия var{ej
} вычисляются только для пути, для которого сумма ожидаемой длительности выполнения процессов максимальна. Если несколько путей имеют равные значения среднего, то выбирается тот, для которого дисперсия больше, поскольку этот путь отражен наименее четко, и поэтому будет вычислена более общая оценка вероятностей.
После того как будет вычислено среднее М{ej
} и дисперсия var{ej
), вероятность того, что узелj будет достигнут в запланированное время Sj
, можно вычислить по формуле
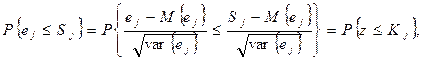 (20) (20)
где z — случайная величина, имеющая стандартное нормальное распределение,
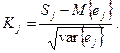 (21) (21)
Случайная величина z имеет среднее 0 и стандартное отклонение 1 .В данном случае использование нормального распределения оправдано тем, что ej
является суммой независимых случайных переменных. Согласно центральной предельной теореме величина еj
приближенно распределена по нормальному закону.
2.3 Метод графической оценки и анализа (GERT)
Метод графической оценки и анализа (метод GERT) применяется в тех случаях организации работ, когда последующие задачи могут начинаться после завершения только некоторого числа из предшествующих задач, причем не все задачи, представленные на сетевой модели, должны быть выполнены для завершения проекта.
Основу применения метода GERT составляет использование альтернативных сетей, называемых в терминах данного метода GERT-cетями.
По существу GERT-сети позволяют более адекватно задавать сложные процессы строительного производства в тех случаях, когда затруднительно или невозможно (по объективным причинам) однозначно определить какие именно работы и в какой последовательности должны быть выполнены для достижения намеченного результата (т.е. существует многовариантность реализации проекта).
Следует отметить, что "ручной" расчет GERT-сетей, моделирующих реальные процессы, чрезвычайно сложен, однако программное обеспечение для вычисления сетевых моделей такого типа в настоящее время, к сожалению, не распространено.
3. Численная реализация задачи сетевого планирования
Каждое событие должно устанавливает завершенность предшествующих действий, например: выбрана цель проекта, обоснованы способы проектирования, рассчитаны показатели конкурентоспособности и т.п. Все события и работы, входящие в заданный комплекс, перечислены в порядке их выполнения.
Сшивание сетевого графика производится на основе приведенного в Таблице 1 перечня выполняемых работ. Построение сети можно начинать как от исходного события, постепенно приближаясь к завершающему, так и, наоборот — от конечного к начальному.
Таблица 1 – Перечень выполняемых проектных работ
| Наименование работ
|
Продолжительность,
Человеко-дней
|
Код
|
| 1 Обоснование цели проекта
|
2
|
0– 1
|
| 2 Проведение маркетинговых
исследований
|
5
|
1– 2
|
| 3 Разработка технических
условий
|
3
|
1– 3
|
| 4 Эскизное проектирование
|
4
|
1 – 4
|
| 5 Выбор поставщиков ресурсов
|
2
|
2 – 5
|
| 6 Фиктивная работа
|
0
|
3 – 9
|
| 7 Техническое проектирование
|
5
|
4 – 6
|
| 8 Расчёт потребности ресурсов
|
2
|
5 – 8
|
| 9 Рабочее проектирование
|
10
|
6 – 7
|
| 10 Закупка производственных
ресурсов
|
10
|
8 – 9
|
| 11 Изготовление деталей
|
8
|
7 – 9
|
| 12 Сертификация деталей
|
2
|
8 – 11
|
Продолжение таблицы 1
| Наименование работ
|
Продолжительность,
Человеко-дней
|
Код
|
| 13 Согласование сроков
поставки
|
3
|
7 – 11
|
| 14 Разработка технологии сборки
|
3
|
9 – 10
|
| 15 Сборка изделия
|
11
|
10 – 11
|
| 16 Отправка продукции
потребителям
|
5
|
11 – 12
|
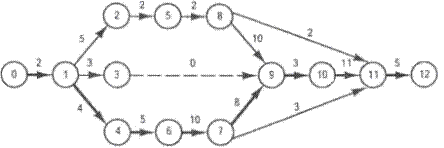
Рисунок 2 - Сетевой график выполнения проекта
На сетевом графике (рисунок 2) критический путь проходит через цепочку событий и работ, обозначенных номерами 0 – 1 – 4 – 6 – 7 – 9 – 10 – 11 – 12, и равен 48 человеко-дням. Он выделен жирной линией.
Расчет ранних сроков выполнения событий ведется от исходного до завершающего таким образом:
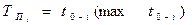 (22) (22)
Расчет ранних сроков свершения событий проводится в прямой последовательности от исходного до конечного.

Ранний срок свершения события 12 соответствует критическому пути сетевого графика: 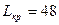 дням. дням.
Остальные полные пути равны:
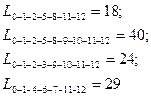
Поздний срок свершения событий определяется разностью между продолжительностью критического пути и максимальной длительностью следующих за данным (i-ым) событием путей к завершающему (С) по следующей формуле:
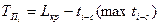 (23) (23)
Расчет поздних сроков свершения событий проводится в обратном порядке от конечного к исходному.
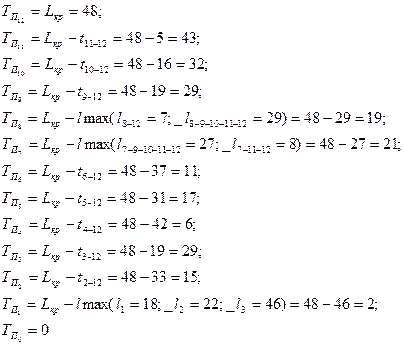
Резервы времени свершения отдельных событий представляют собой разность между поздними и ранними сроками их выполнения,
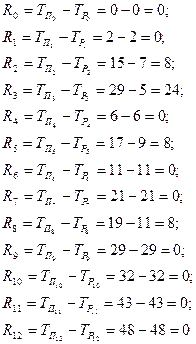
Расчет резервов времени подтверждает, что критический путь проходит в сетевом графике через события 0 – 1 – 4 – 6 – 7 – 9 – 10 – 11 – 12 с нулевыми значениями резервов времени. В таблице 2 приведены основные параметры сетевого графика, характеризующие продолжительность выполняемых работранние и поздние сроки свершения событий, а также имеющиеся в сетевой модели резервы времени (Рисунок 2).
Полный резерв пути показывает, на сколько в сумме может быть увеличена продолжительность всех работ, принадлежащих данному пути. В соответствии с ранее выполненными расчетами полных путей нашего сетевого графика найдем полные резервы времени всех четырех путей.
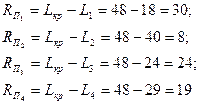
Выполненные расчеты основных параметров сетевых графиков должны быть использованы при анализе и оптимизации сетевых стратегических планов.
| Код работ
|
Продолжительность
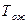
|
№
события
|
Показатели событий
|
| Ранний срок 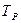
|
Поздний срок 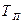
|
Резерв
времени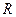
|
| 0-1
|
2
|
0
|
0
|
0
|
0
|
| 1-2
|
5
|
1
|
2
|
2
|
0
|
| 1-3
|
3
|
2
|
7
|
15
|
8
|
| 1-4
|
4
|
3
|
5
|
29
|
24
|
| 2-5
|
2
|
4
|
6
|
6
|
0
|
| 4-6
|
5
|
5
|
9
|
17
|
8
|
| 5-8
|
2
|
6
|
11
|
11
|
0
|
| 6-7
|
10
|
7
|
21
|
21
|
0
|
| 7-9
|
8
|
8
|
11
|
19
|
8
|
| 8-9
|
10
|
9
|
29
|
29
|
0
|
| 9-10
|
3
|
10
|
32
|
32
|
0
|
| 10-11
|
11
|
11
|
43
|
43
|
0
|
| 11-12
|
5
|
12
|
48
|
48
|
0
|
Таблица 2 – Расчётные параметры сетевого графика (в человеко-днях)
Расчет и анализ коэффициентов напряженности сетевых путей наряду с резервами времени позволяет распределить все работы по трем зонам: критическая, подкритическая и резервная. В разработанном нами графике коэффициенты напряженности всех путей будут иметь следующие значения.
Первый путь проходит через события 0 – 1 – 2 – 5 – 8 – 11 – 12, и равен 18 человеко-дням. Коэффициент напряженности этого пути составляет:
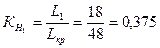 (24) (24)
Второй путь,
проходящий через события 0 – 1 – 2 – 5 – 8 – 9 – 10 – 11 – 12, равен 40 дням, а коэффициент напряженности — 0,833.
Третий путь,
равный 24 дням, пролегает по событиям 0 – 1 – 3 – 9 – 10 – 11 – 12. Коэффициент его напряженности имеет значение 0,5.
Четвертый путь —
это критический путь, коэффициент напряженности которого равен 1,0.
Пятый путь объединяет события 0 – 1 – 4 – 6 – 7 – 11 – 12. Продолжительность этого пути составляет 29 дней, а коэффициент напряженности — 0,604.
Проведенный анализ коэффициентов напряженности путей подтверждает возможность сокращения критического пути почти в три раза при более рациональной загрузке имеющихся трудовых ресурсов. Однако при этом следует иметь в виду, как существующие функциональные формы специализации персонала, так и уровень требуемой квалификации специалистов. Из расчетов следует, что наименее напряженными оказались пути выполнения плановых работ, а наиболее напряженными — проектно-конструкторских. Но в реальных условиях вряд ли имеется возможность совмещения своих функций работниками планово-экономических, и проектно-конструкторских подразделений предприятия. Это означает, что при необходимости сокращения критического пути, например на 24 дня, следует при односменной работе дополнительно привлечь одного конструктора на целый месяц. Возможны и многие иные варианты сокращения критического пути с 48 человеко-дней до необходимого или планируемого значения.
Заключение
Диапазон применения сетевого планирования и управления весьма широк: от задач, касающихся деятельности отдельных лиц, до проектов, в которых участвуют сотни организаций и десятки тысяч людей (например, разработка и создание крупного территориально-промышленного комплекса).
Методы сетевого планирования и управления обеспечивают руководителей и исполнителей на всех участках работы обоснованной информацией, которая необходима им для принятия решений по планированию, организации и управлению. А при использовании вычислительной техники сетевое планирование и управление является уже не просто одним из методов планирования, а автоматизированным методом управления производственным процессом.
Сетевые модели могут быть широко использованы на всех отечественных предприятиях при разработке как долгосрочных, так и текущих планов. Сетевое планирование позволяет не только определять потребность различных производственных ресурсов в будущем, но и координировать их рациональный расход в настоящем. С помощью сетевых графиков можно соединить в единую систему все материальные, трудовые, финансовые и многие другие ресурсы и средства производства и в идеальных (планируемых), и в реальных (существующих) экономических условиях.
После составления сетевого плана производится его оптимизация. Ее цель - так распределить имеющиеся ресурсы, чтобы уменьшить критический путь.
Существуют различные методы сетевого планирования.
Метод критического пути позволяет рассчитать возможные календарные графики выполнения комплекса работ на основе описанной логической структуры сети и оценок продолжительности выполнения каждой работы, определить критический путь для проекта в целом.
Метод PERT - метод событийного сетевого анализа, используемый для определения длительности программы при наличии неопределенности в оценке продолжительностей индивидуальных операций. PERT основан на методе критического пути, длительность операций в котором рассчитывается как взвешенная средняя оптимистического, пессимистического и ожидаемого прогнозов. PERT рассчитывает стандартное отклонение даты завершения от длительности критического пути.
В настоящее время происходит расширение методов и приемов использования сетевых методов.
Список использованных источников
1. Алексинская Т.В. Учебное пособие по решению задач по курсу "Экономико-математические методы и модели". Таганрог: Изд-во ТРТУ, 2002, 153 с.
2. Голенко Д. И. Статистические методы сетевого планирования и управления. Москва: издательство Наука, 1968, 400с.
3. Кофман А., Дебазей Г. Сетевые методы планирования и их применение. Москва: Издательство Прогресс, 1968, 180с.
4. Заболотский В.П., Оводенко А.А., Степанов А.Г. Математические модели в управлении: Учеб. пособие/ СПбГУАП. СПб., 2001, 196с.: ил.
5. Ивасенко А.Г. Управление проектами: учебное пособие/А.Г. Ивасенко, Я.И.Никонова, М.В.Каркавин – Ростов н/Дону:Феникс, 2009. – 330 с. – Высшее образование.
6. Кудрявцев Е.М. Microsoft Project. Методы сетевого планирования и управления проектом. – М.: ДМК Пресс, 2005. – 240 с., ил.
7. Мазур И.И., Шапиро В.Д., Ольдерогге Н.Г. Управление проектами: Ученое пособие/ Под общ. ред. И.И.Мазура. – 3-е изд. – М.: Омега-Л, 2004. – с. 664.
8. Тынкевич М.А. Экономико-математические методы (исследование операций). Изд. 2, испр. и доп. - Кемерово, 2000. -177 c. ISBN 5-89070-043-X
9. Управление проектом. Основы проектного управления: ученик/ кол. авт.: под ред. проф. М.Л.Разу. – М.: КНОРУС, 2006. – 768 с.
10. Метод критического пути. http://ru.wikipedia.org/wiki/Метод_критического_пути
11. Сетевое планирование. http://ru.wikipedia.org/wiki/Сетевое_планирование
12. Ребрин Ю.И.. Основы экономики и управления производством. Сетевое планирование и управление. http://polbu.ru/rebrin_management/ch24_all.html
|