Министерство сельского хозяйства Российской Федерации
Департамент кадровой политики и образования
ФГОУ ВПО Ижевская ГСХА
кафедра высшей математики
Реферат по высшей математике
Функции
нескольких
переменных в
экономических
задачах
Выполнил: студентка 914 группы
Харина Светлана Анатольевна
Проверил: ст. преподаватель
Иванова И.А.
Ижевск 2007
Оглавление
1. Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
2. Справочный материал . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
3. Решение задач . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
4. Литература . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
Введение
Использование функций нескольких переменных —
широко применяемый для экономического анализа математический метод. Базовой задачей экономического анализа является изучение экономических величин, записываемых в виде функций. В каком направлении изменится доход государства при увеличении налогов или при введении импортных пошлин? Увеличится или уменьшится выручка фирмы при повышении цены на ее продукцию? Для решения подобных задач должны быть построены функции связи входящих в них переменных, которые затем изучаются с помощью методов дифференциального исчисления.
В экономике очень часто требуется найти оптимальное значение того или иного показателя: наивысшую производительность труда, максимальную прибыль, максимальный выпуск, минимальные издержки и т.д. Каждый показатель представляет собой функцию одного или нескольких аргументов. Например, выпуск можно рассматривать как функцию затрат труда и капитала (как это делается в производственных функциях). Поскольку экономические показатели обычно зависят от многих факторов, нахождение оптимального значения показателя сводится к нахождению экстремума (максимума или минимума) функции одной или нескольких переменных.
Такие задачи хорошо изучены теорией функций нескольких переменных, использующей методы дифференциального исчисления. Многие задачи включают не только максимизируемую (минимизируемую) функцию, но и ограничения (например, бюджетное ограничение в задаче потребительского выбора).
Реклама

Справочный материал
Рассмотрим некоторые приложения функций нескольких переменных в экономической теории.
Производственной функцией
называется зависимость результата производственной деятельности — выпуска продукции и от обусловивших его факторов — затрат ресурсов x
1
,
x
2
, …,
xn
.
Производственная функция может быть задана как в натуральных, так и в денежных единицах. В последнем случае она представляет собой доход oт использования ресурсов.
Производственная функция К(х, у) = Ах а
у β
называется функцией Ко6ба—Дугласа.
Параметры α
и β
представляют собой частные эластичности выпуска продукции по отношению к затратам труда х
и капитала у
.
Функция полезности
U
(
x
1
, х2
, …, хп
)
задает полезность для потребителя от приобретения х1
единиц 1-го блага, х2
единиц 2-го блага и т.д.
Функция издержек С(х)
определяет затраты, необходимые для производства х
единиц данного продукта. Прибыль Р(х)=
D
(
x
) -
C(x
), где D
(
x
)
— доход от производства х
единиц продукта.
Оптимальным значением
выпуска для производителя является то значение х
единиц продукта, при котором прибыль Р(х)
оказывается наибольшей.
Значительная часть экономических механизмов иллюстрируется на рисунках, изображающих линии уровня функции двух переменных z
=
f
(
x
,
у).
Например, линии уровня производственной функции называются изоквантами.
Пусть х
и у —
два различных фактора производства, а функция z
=
f
(
x
,
у)
характеризует выпуск продукции, который позволяют значения факторов х
и у.
На рис.1 линии уровня f
(
x
,
y
)=
Q
изображены сплошными линиями, а штриховкой выделена так называемая экономическая область,
которая характеризуется тем, что высекаемые ею части изоквант представляют собой графики убывающих функций, т.е. увеличение количества одного факторапозволяет уменьшить количество другого, не меняя размера выпуска, Иными словами, экономическая область — это множество значений факторов, допускающих замещение одного из них другим.
Очевидно, что все "разумные" значения х
и у
принадлежат экономической области.
 
Изокванты позволяют геометрически иллюстрировать решение задачи об оптимальном распределении ресурсов. Пусть z
=
g
(
x
,
y
)
— функция издержек, характеризующая затраты, необходимые для обеспечения значений ресурсов x
и у
(часто можно считать, что функция издержек линейная: g
(
x
,
y
)= рх
х
+ ру
у,
где рх
и ру
-
"цены" факторов х
и у).
Линии уровня этой функции также изображены на рис. 1 Комбинации линий уровня функции f
(
x
)
и g
(
x
)
позволяют делать выводы о предпочтительности того или иного значения факторов х
и у.
Очевидно, например, что пара значений (х1
,у1
)
более предпочтительна, чем пара (х2
,
y
2
),
так как обеспечивает тот же выпуск, но с меньшими затратами. Оптимальными же значениями факторов будут значения (х0
, y
0
) —
координаты точки касания линии уровня функции выпуска и функции издержек.
Реклама

  Линии уровня функции полезности (они называются кривыми безразличия
)
также позволяют рассматривать вопросы замещения одного товара другим и иллюстрировать решение задачи об оптимальном потреблении (потребительского выбора) (см. рис. 2). Линии уровня функции полезности (они называются кривыми безразличия
)
также позволяют рассматривать вопросы замещения одного товара другим и иллюстрировать решение задачи об оптимальном потреблении (потребительского выбора) (см. рис. 2).

Линия уровня затрат на приобретение товаров х
, у
изображены на рис. 2 пунктиром. Оптимальное потребление обеспечивается значением (
х0
, y
0
)
— координатами точки касания кривой безразличия и линии уровня затрат. В этой точке заданная полезность достигается наиболее экономичным образом.
Решение задач
Задача 1.
Найти значения величин используемых ресурсов (х
, у),
при которых фирма-производитель получит максимальную прибыль, если заданы производственная функция К(х, у)
и цены р1
и р2
на единицупервого и второго ресурсов:
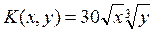 , р1
=4, р2
=1/48 , р1
=4, р2
=1/48
Решение.
Производственная функция в денежном выражении равна доходу от использования ресурсов. Так как функция С(х) = р1
х+р2
у,  С(х) = 4х+1/48у.
Таким образом, функция прибыли равна (П(х)=
D
(
x
) -
C(x
)):
С(х) = 4х+1/48у.
Таким образом, функция прибыли равна (П(х)=
D
(
x
) -
C(x
)):
π
(х,у) =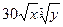 - 4
x
- 1/48
y
. - 4
x
- 1/48
y
.
Требуется найти значения величин используемых ресурсов (х
, у),
при которых фирма-производитель получит максимальную прибыль, т.е. надо исследовать функцию π
(х,у)
на экстремум. Сначала определим стационарные точки функции. Для этого найдем частные производные функции и приравняем их к 0 (по необходимому условию существования экстремума).
π
х
’ =15
y
1/3
x
-1/2
- 4
π
y
’ =10
y
-2/3
x
1/2
– 1/48
Так какπ
х
’=0;
π
y
’=0 
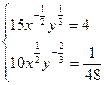 => => 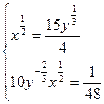
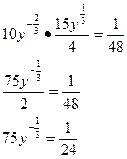
y
=183
•106
;
x
=225•4502
(225•4502
; 183
•106
) – стационарная точка
По достаточному условию существования экстремума чтобы определить существует ли экстремум, надо составить определитель второго порядка 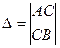 . .
Где А=π
х
x
’’ =-15/2
y
1/3
x
-3/2
В=π
yy
’’ =-20/3
y
-5/3
x
1/2
С=π
xy
’’ =
π
yx
’’= 5
y
-2/3
x
-1/2
Составим определитель: ∆=
π
х
x
’’
π
yy
’’-
(π
xy
’’)2
=
= 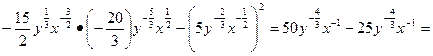 25
x
-1
y
-4/3
>0 25
x
-1
y
-4/3
>0 
экстремум есть. Так как А=-
15/2
y
1/3
x
-3/2
<0
 max max
Таким образом, найденная критическая точка есть точка максимума (по достаточному условию экстремума функции двух переменных)
Ответ: x=225•4502
; y=183
•106
Задача 2.
Заданы производственная функция, цены на единицу первого и второго ресурсов, а также ограничения I
в сумме, которая может быть потрачена на приобретение ресурсов (сумма ≤
I
). Найти значения величин используемых ресурсов (х, у),
при которых фирма-производитель получит наибольшую прибыль:
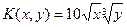 , p1
=2, p2
=4, I=12. , p1
=2, p2
=4, I=12.
Решение.
Следует максимизировать функцию π
(х,у) =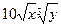 -2
x
-4
y
; -2
x
-4
y
;
(П(х,
y
)=
D
(
x
,
y
)-
C
(
x
,
y
)), но при условии, что C
(
x
,
y
) ≤
I
 2х + 4у ≤ 12. 2х + 4у ≤ 12.
Итак, имеем задачу максимизации функции π
(х,у) =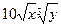 -2
x
-4
y
,
т.е. надо найти глобальный экстремум в области, ограниченной прямой 2х + 4у ≤ 12
, или х≤6-2у
, осью ОХ
и осью ОУ
(так как x>0, y>0). -2
x
-4
y
,
т.е. надо найти глобальный экстремум в области, ограниченной прямой 2х + 4у ≤ 12
, или х≤6-2у
, осью ОХ
и осью ОУ
(так как x>0, y>0).
Построим этот график:
а) Найдем стационарные точки внутри области Д
(найдем π
х
’
и π
y
’
и приравняем к 0):
π
х
’=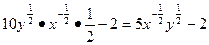
π
y
’
=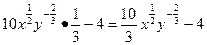
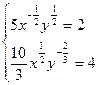 ; ; 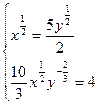 ; ;
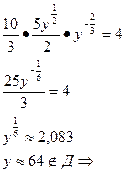
стационарных точек нет.
б) Найдем стационарные точки на границах области:
· x=6-2y
 П= П=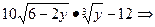
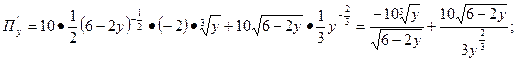
П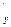 =0 =0

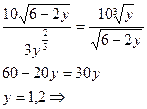
x
=6-2•1,2=3,6 (3,6; 1,2) –
стационарная точка 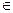 обл. Д
и х=6-2у обл. Д
и х=6-2у
· х=0 (
ось ОУ)
 П=-4
y П=-4
y

П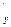 =-4
≠
0
=-4
≠
0
 стационарных точек нет стационарных точек нет
· у=0 (
ось ОХ)
 П=-2х П=-2х

П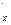 =-2 ≠ 0 =-2 ≠ 0
 стационарных точек нет стационарных точек нет
↓
Найдена одна стационарная точка (3,6;1,2), которая показывает сочетания величин х
и у
(используемых ресурсов), при которых фирма получит наибольшую прибыль. При этом фирма потратит всю выделенную на это сумму – 12.
Ответ: x=3,6, y=1,2.
Задача 3.
Потребитель имеет возможность потратить сумму 1000 ден. ед. на приобретение х
единиц первого товара и у
единиц второго товара. Заданы функция полезности U
(
x
, у)
и цены p
1
,
р2
за единицу соответственно первого и второго товаров. Найти значения (х,
у)
, при которых полезность для потребителя будет наибольшей:
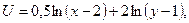 p1
=0,2, p2
=4. p1
=0,2, p2
=4.
Решение.
Рассмотрим линии уровня функции полезности U
(
x
,у)
=С, т.е. 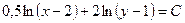 (С=
const
). Используя свойства логарифмов, имеем: (С=
const
). Используя свойства логарифмов, имеем:
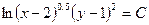 , т.е. , т.е. 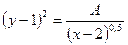 , где , где 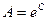
Таким образом, линии уровня представляют собой график функции
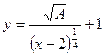 (кривая безразличия) (кривая безразличия)
Легко видеть, что максимальное значение A
, а следовательно, и уровня С
достигается в том случае, если соответствующая кривая безразличия касается прямой (линии уровня затрат) 0,2х+
4у =1000.
Так как градиент в каждой точке перпендикулярен линии уровня, то из этого следует, что условие максимальности прибыли может быть сформулировано следующим образом:
gradU
(
x
,
y
)
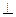 (0,2
x
+4
y
=1000
) (0,2
x
+4
y
=1000
)
Так как у=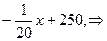
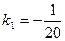 . Угловой коэффициентпрямой, проходящей через gradU
равен . Угловой коэффициентпрямой, проходящей через gradU
равен 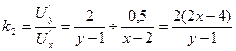 . .
Из условия перпендикулярности прямых имеем  т.е. т.е.
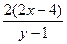 =20
, =20
,  x
-5
y
=-3 x
-5
y
=-3
Следовательно, оптимальное распределение потребления товаров находится как решение системы:
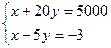 т.е. т.е.
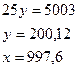
Ответ: x=997,6; Y=200,12 - значения, при которых полезность для потребителя будет наибольшей.
Задача 4.
Прибыль П
автомобильного завода от производства одного автомобиля определяется формулой 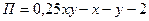 , где x
–
затраты на материалы, млн. руб., (х>0), у –
затраты на оплату рабочей силы, млн. руб., (у>0),2 млн. руб. – постоянные затраты. , где x
–
затраты на материалы, млн. руб., (х>0), у –
затраты на оплату рабочей силы, млн. руб., (у>0),2 млн. руб. – постоянные затраты.
Значения х
и у
, при которых прибыль завода максимальна, а суммарные затраты на один автомобиль не превышают 27 млн. руб. равны…
Решение.
Известно, что 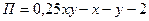 . Так как П(х,
y
)=
D
(
x
,
y
)-
C
(
x
,
y
) . Так как П(х,
y
)=
D
(
x
,
y
)-
C
(
x
,
y
)  С=х+у+2,
но при этом С≤
27 млн. руб. С=х+у+2,
но при этом С≤
27 млн. руб.  Следует максимизировать функцию Следует максимизировать функцию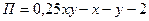 , но при условии, что х+у+2≤ 27. , но при условии, что х+у+2≤ 27.
Итак, имеем задачу максимизации функции, т.е. надо найти глобальный экстремум для П(х,
y
)
в области, ограниченной прямой x
+
y
≤25
, осью ОХ
и ОУ
(так как х>0,
y
>0
). Построим этот график:
а) Найдем стационарные точки внутри области Д.
Для этого найдем π
х
’
и π
y
’
и приравняем к 0:
π
х
’=0,25
y
-1
π
y
’
=0
,
2
5x-1
π
х
’
=0
;
π
y
’=0

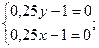 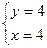 (4;4) – стационарная точка (4;4) – стационарная точка
П(4;4)=0,25•4•4-4-4-2=-6
б) Найдем стационарные точки на границах:
· у
=
25-х
 П= П=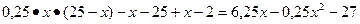
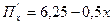 П П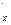 =0 =0

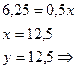
(12,5;12,5) –
стационарная точка 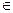 обл. Д
и у=25-х обл. Д
и у=25-х
П(12,5;12,5)=0,25•12,5•12,5-12,5-12,5-2=12,0625
· х=0 (
ось ОУ)
 П=-у-2 П=-у-2

П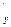 =-
1
≠
0
=-
1
≠
0
 стационарных точек нет стационарных точек нет
· у=0 (
ось ОХ)
 П=-х-2 П=-х-2

П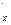 =-1 ≠ 0 =-1 ≠ 0
 стационарных точек нет стационарных точек нет 
П(4;4)<П(12,5;12,5)

П(4;4)=-6 –
минимальное значение функции
П(12,5;12,5)=12
-
максимальное значение функции, при котором прибыль фирмы будет максимальна, и затраты на 1 автомобиль будут составлять27 млн. руб.
Ответ: x=12,5, y=12,5
Задача 5.
Издержки предприятия на изготовление единицы некоторого вида продукции определяются формулой 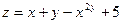 ; где х
– затраты капитала, тыс. руб., (х>0
), у
– расходы на оплату рабочей силы, тыс. руб., (у>0
). При каких значениях х
и у
издержки производства будут минимальными, если затраты х+у
на единицу продукции составляют 3 тыс. руб.? ; где х
– затраты капитала, тыс. руб., (х>0
), у
– расходы на оплату рабочей силы, тыс. руб., (у>0
). При каких значениях х
и у
издержки производства будут минимальными, если затраты х+у
на единицу продукции составляют 3 тыс. руб.?
Решение.
Известно, что 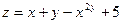 . Имеем задачу минимизации функции при х+у=3
или y
=3-
x
, . Имеем задачу минимизации функции при х+у=3
или y
=3-
x
,
 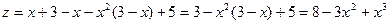
Исследуем функцию на монотонность:
z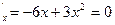
 x=0
и x=2 x=0
и x=2
 y=3-2=1 y=3-2=1
Ответ: х
=2; у
=1
Литература
1. Кремер Н.Ш. Высшая математика для экономистов: Учебник для вузов. – М.: ЮНИТИ, 2003. – 471 с.
2. Кремер Н.Ш. Практикум по высшей математике для экономистов: Учебное пособие для вузов. – М.: ЮНИТИ-ДАНА, 2004. – 423 с.
|