МИНИСТЕРСТВО ОБРАЗОВАНИЯ УКРАИНЫ
Харьковский государственный технический университет радиоэлектроники
Расчетно‑пояснительная записка
к курсовой работе
по курсу «Основы радиоэлектроники»
Тема: Расчёт частотных и временных характеристик линейных цепей
Вариант №34
| Выполнил:
студент группы БЭА‑98‑1
Дмитренко С.Н.
|
Консультант:
доц. Олейников А.Н.
|
2000
СОДЕРЖАНИЕ
| ВВЕДЕНИЕ
|
3
|
| ЗАДАНИЕ
|
4
|
| 1 РАСЧЁТ КОМПЛЕКСНОГО ВХОДНОГО СОПРОТИВЛЕНИЯ ЦЕПИ
|
5
|
| 1.1 Определение комплексного входного сопротивления цепи
|
5
|
| 1.2 Определение активной составляющей комплексного входного сопротивления цепи
|
6
|
| 1.3 Определение реактивной составляющей комплексного входного сопротивления цепи
|
7
|
| 1.4 Определение модуля комплексного входного сопротивления цепи
|
9
|
| 1.5 Определение аргумента комплексного входного сопротивления цепи
|
10
|
| 2 РАСЧЁТ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ЦЕПИ
|
12
|
| 2.1 Определение комплексного коэффициента передачи цепи
|
12
|
| 2.2 Определение амплитудно-частотной характеристики цепи
|
12
|
| 2.3 Определение фазочастотной характеристики цепи
|
14
|
| 3 РАСЧЕТ ВРЕМЕННЫХ ХАРАКТЕРИСТИК ЦЕПИ
|
16
|
| 3.1 Определение переходной характеристики цепи
|
16
|
| 3.2 Определение импульсной характеристики цепи
|
19
|
| 3.3 Расчет отклика цепи на заданное воздействие методом интеграла Дюамеля
|
22
|
| ВЫВОДЫ
|
27
|
| СПИСОК ИСПОЛЬЗОВАНЫХ ИСТОЧНИКОВ
|
28
|
ВВЕДЕНИЕ
Знание фундаментальных базовых дисциплин в подготовке и формировании будущего инженера-конструктора весьма велико.
Дисциплина «Основы радиоэлектроники» (ОРЭ) относится к числу базовых дисциплин. При изучении данного курса приобретаются теоретические знания и практические навыки по использованию этих знаний для расчета конкретных электрических цепей.
Основная цель курсовой работы – закрепление и углубление знаний по следующим разделам курса ОРЭ:
расчет линейных электрических цепей при гармоническом воздействием методом комплексных амплитуд;
частотные характеристики линейных электрических цепей;
временные характеристики цепей;
методы анализа переходных процессов в линейных цепях (классический, интегралы наложения).
Курсовая работа закрепляет знания в соответствующей области, а тем у кого никаких знаний нет предлагается их получить практическим методом – решением поставленных задач.
ЗАДАНИЕ
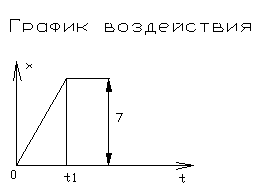 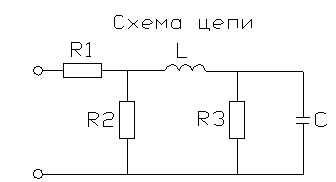
Вариант № 34
| R1, Ом
|
4,5
|
t1, мкс
|
30
|
| R2, Ом
|
1590
|
I1, А
|
7
|
| R3, Ом
|
1100
|
| L, мкГн
|
43
Реклама

|
| C, пФ
|
18,8
|
| Реакция
|
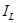
|
Задание:
1. Определить комплексное входное сопротивление цепи.
2. Найти модуль, аргумент, активную и реактивную составляющие комплексного сопротивления цепи.
3. Расчет и построение частотных зависимостей модуля, аргумента, активной и реактивной составляющих комплексного входного сопротивления.
4. Определить комплексный коэффициент передачи цепи, построить графики амплитудно-частотной (АЧХ) и фазочастотной (ФЧХ) характеристик.
5. Определить классическим методом переходную характеристику цепи и построить ее график.
6. Найти импульсную характеристику цепи и построить ее график.
7. Рассчитать отклик цепи на заданное воздействие и построить график отклика.
1 РАСЧЁТ КОМПЛЕКСНОГО ВХОДНОГО СОПРОТИВЛЕНИЯ ЦЕПИ
1.1 Определение комплексного входного сопротивления цепи
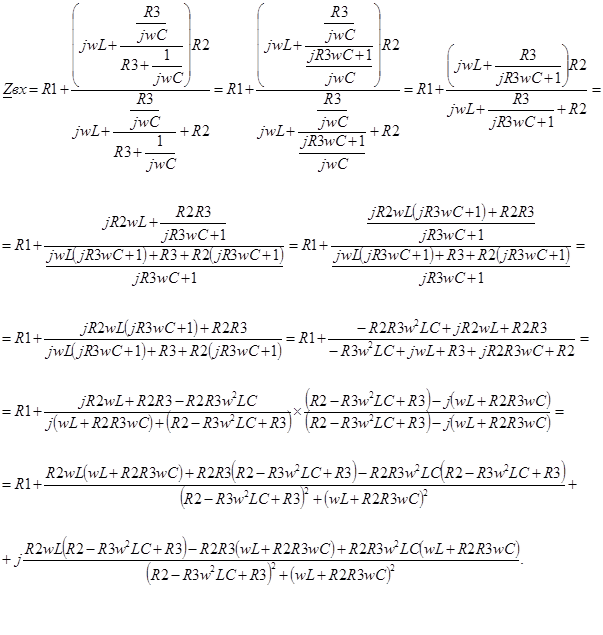 (1) (1)
После подстановки числовых значений получим:
 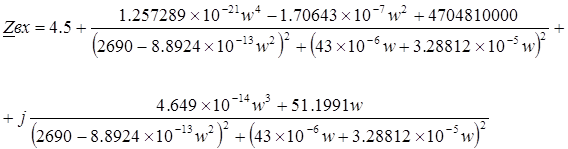 (2) (2)
1.2 Определение активной составляющей комплексного входного сопротивления цепи
Из (2) видно, что активная составляющая комплексного входного сопротивления цепи равна:
| 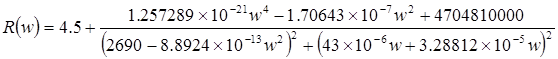
|
(3)
|
Результаты расчётов приведены в таблице 1.1, а кривая, построенная на основании результатов, имеет вид графика изображённого на рисунке 1.1
| Таблица 1.1
|
Зависимость активной составляющей от частоты
|
| w, рад/c
|
R(w), Ом
|
| 0
|
654.6858736
|
| 1*10^7
|
644.7488512
|
| 2*10^7
|
628.547516
|
| 3*10^7
|
640.8052093
|
| 4*10^7
|
711.6552945
|
| 5*10^7
|
835.0124845
|
| 6*10^7
|
975.66653
|
| 7*10^7
|
1103.2978887
|
| 8*10^7
|
1206.27837
|
| 9*10^7
|
1285.1867918
|
| 1*10^8
|
1344.7103773
|
| 1.1*10^8
|
1389.7224921
|
| 1.2*10^8
|
1424.132605
|
| 1.3*10^8
|
1450.8140349
|
| 1.4*10^8
|
1471.8158424
|
| 1.5*10^8
|
1488.5909995
|
| 1.6*10^8
|
1502.175626
|
| 1.7*10^8
|
1513.316686
|
| 1.8*10^8
|
1522.5598201
|
| 1.9*10^8
|
1530.3091743
|
| 2*10^8
|
1536.8682451
|
| 2.1*10^8
|
1542.4679891
|
| 2.2*10^8
|
1547.2863847
|
| 2.3*10^8
|
1551.4622108
|
| 2.4*10^8
|
1555.104878
|
| 2.5*10^8
|
1558.3015308
|
| 2.6*10^8
|
1561.1222429
|
| 2.7*10^8
|
1563.623861
|
| 2.8*10^8
|
1565.8528828
|
| 2.9*10^8
|
1567.8476326
|
| 3*10^8
|
1569.6399241
|
| 3.1*10^8
|
1571.2563425
|
| 3.2*10^8
|
1572.7192423
|
| 3.3*10^8
|
1574.04753
|
| 3.4*10^8
|
1575.2572835
|
| 3.5*10^8
|
1576.3622454
|
| 3.6*10^8
|
1577.3742185
|
| 3.7*10^8
|
1578.3033862
|
| 3.8*10^8
|
1579.1585717
|
| 3.9*10^8
|
1579.9474512
|
| 4*10^8
|
1580.676728
|
| 4.1*10^8
|
1581.3522774
|
| 4.2*10^8
|
1581.9792664
|
| 4.3*10^8
|
1582.5622541
|
| 4.4*10^8
|
1583.1052755
|
| 4.5*10^8
|
1583.6119126
|
| 4.6*10^8
|
1584.0853538
|
| 4.7*10^8
|
1584.5284451
|
| 4.8*10^8
|
1584.9437332
|
| 4.9*10^8
|
1585.3335025
|
| 5*10^8
|
1585.699807
|
| 
|
1594.5
|
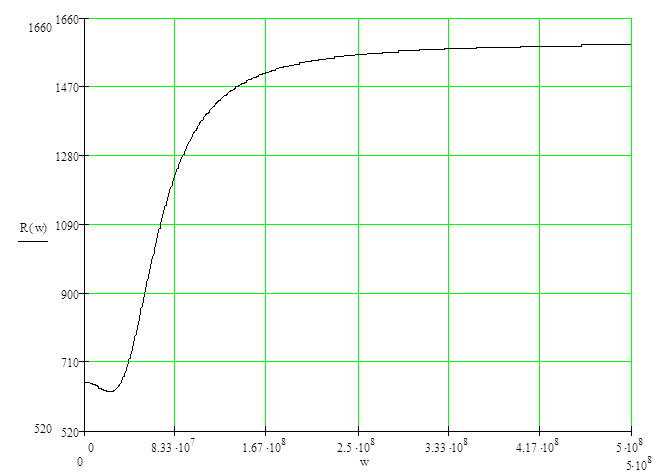
Рисунок 1.1 ‑ Зависимость активной составляющей от частоты; размерность R(w) – Ом, w – рад/с
1.3 Определение реактивной составляющей комплексного входного сопротивления цепи
Из (2) видно, что реактивная составляющая комплексного входного сопротивления цепи равна:
Реклама

| 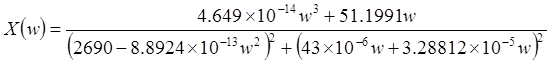
|
(4)
|
Результаты расчётов приведены в таблице 1.2, а кривая, построенная на основании результатов, имеет вид графика изображённого на рисунке 1.2
Таблица 1.2
|
Зависимость реактивной составляющей от частоты
|
| w, рад/с
|
X(w), Ом
|
| 0
|
0
|
| 2.5*10^7
|
246.0721781
|
| 7.5*10^7
|
621.5367231
|
| 1*10^8
|
537.3271164
|
| 1.5*10^8
|
383.2305778
|
| 1.75*10^8
|
331.4740341
|
| 2.25*10^8
|
259.7380449
|
| 2.5*10^8
|
234.1512213
|
| 3*10^8
|
195.4771722
|
| 3.25*10^8
|
180.5329631
|
| 3.5*10^8
|
167.7003466
|
| 3.75*10^8
|
156.564089
|
| 4*10^8
|
146.8103054
|
| 4.5*10^8
|
130.5374047
|
| 4.75*10^8
|
123.6804004
|
| 5*10^8
|
117.5068169
|
| 5.25*10^8
|
111.9195119
|
| 5.75*10^8
|
102.199084
|
| 6*10^8
|
97.9451927
|
| 6.5*10^8
|
90.4174982
|
| 6.75*10^8
|
87.071266
|
| 7.25*10^8
|
81.070308
|
| 7.5*10^8
|
78.3695601
|
| 8*10^8
|
73.4739969
|
| 8.25*10^8
|
71.2485584
|
| 8.75*10^8
|
67.1789125
|
| 9*10^8
|
65.313547
|
| 9.5*10^8
|
61.8771764
|
| 1*10^9
|
58.7842651
|
| 
|
0
|
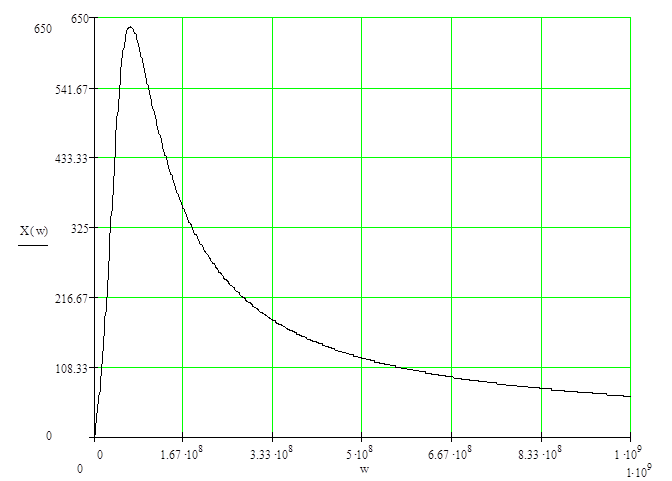
Рисунок 1.2‑ Зависимость реактивной составляющей от частоты; размерность X(w) – Ом, w – рад/с
1.4 Определение модуля комплексного входного сопротивления цепи
Модуль комплексного входного сопротивления цепи:
| 
|
(5)
|
Подставляя выражения (3) и (4) получим:
| 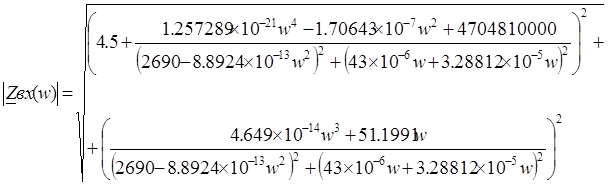
|
(6)
|
Результаты расчётов приведены в таблице 1.3, а кривая, построенная на основании результатов, имеет вид графика изображённого на рисунке 1.3
| Таблица 1.3
|
Зависимость модуля от частоты
|
| w, рад/с
|
ModZ(w), Ом
|
| 0
|
654.6858736
|
| 1*10^7
|
649.2212009
|
| 1.42*10^7
|
647.35766‑min
|
| 3*10^7
|
715.7636509
|
| 4*10^7
|
849.7354647
|
| 6*10^7
|
1158.5565761
|
| 7*10^7
|
1270.5610656
|
| 9*10^7
|
1407.7765634
|
| 1*10^8
|
1448.0906149
|
| 1.2*10^8
|
1498.7078464
|
| 1.3*10^8
|
1514.9060929
|
| 1.5*10^8
|
1537.1300659
|
| 1.6*10^8
|
1544.9118415
|
| 2*10^8
|
1564.25307
|
| 2.1*10^8
|
1567.2999067
|
| 2.3*10^8
|
1572.1477461
|
| 2.4*10^8
|
1574.0946495
|
| 2.6*10^8
|
1577.2894385
|
| 2.7*10^8
|
1578.6096652
|
| 2.9*10^8
|
1580.827954
|
| 3*10^8
|
1581.7650952
|
| 3.2*10^8
|
1583.3693222
|
| 3.3*10^8
|
1584.059005
|
| 3.5*10^8
|
1585.257498
|
| 3.6*10^8
|
1585.7801122
|
| 3.8*10^8
|
1586.699579
|
| 3.9*10^8
|
1587.1052533
|
| 4.1*10^8
|
1587.8264025
|
| 4.2*10^8
|
1588.1477312
|
| 4.4*10^8
|
1588.7239824
|
| 4.5*10^8
|
1588.9829149
|
| 4.6*10^8
|
1589.2246865
|
| 4.7*10^8
|
1589.4507882
|
| 4.8*10^8
|
1589.6625517
|
| 4.9*10^8
|
1589.8611698
|
| 5*10^8
|
1590.0477131
|
| 
|
1594.5
|

Рисунок 1.3 ‑ Зависимость модуля от частоты; размерность ModZ(w) – Ом,
w – рад/с
1.5 Определение аргумента комплексного входного сопротивления цепи
Аргумент комплексного входного сопротивления цепи:
| 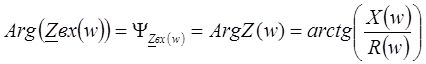
|
(7)
|
Подставляя выражения (3) и (4) получим:
| 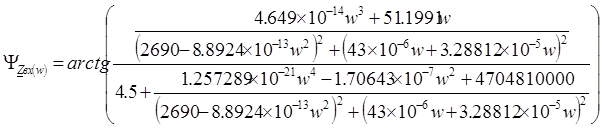
|
(8)
|
Результаты расчётов приведены в таблице 1.4, а кривая, построенная на основании результатов, имеет вид графика изображённого на рисунке 1.4
| Таблица 1.4
|
Зависимость аргумента от частоты
|
| w, рад/c
|
ArgZ(w),рад
|
| 0
|
0
|
| 1*10^7
|
0.1174454
|
| 2*10^7
|
0.2790074
|
| 3*10^7
|
0.4617485
|
| 4*10^7
|
0.5781004
|
| 5*10^7
|
0.6013055
|
| 6*10^7
|
0.5695574
|
| 7*10^7
|
0.5189209
|
| 8*10^7
|
0.4671155
|
| 9*10^7
|
0.4204151
|
| 1*10^8
|
0.3801492
|
| 1.3*10^8
|
0.2919224
|
| 1.4*10^8
|
0.2705269
|
| 1.6*10^8
|
0.2357585
|
| 1.8*10^8
|
0.2088236
|
| 1.9*10^8
|
0.1975292
|
| 2*10^8
|
0.1873925
|
| 2.2*10^8
|
0.1699518
|
| 2.3*10^8
|
0.1623974
|
| 2.4*10^8
|
0.1554881
|
| 2.6*10^8
|
0.1433007
|
| 2.7*10^8
|
0.1378992
|
| 2.8*10^8
|
0.1328918
|
| 3*10^8
|
0.1238984
|
| 3.2*10^8
|
0.1160497
|
| 3.3*10^8
|
0.1124883
|
| 3.4*10^8
|
0.1091398
|
|  
|
0
|
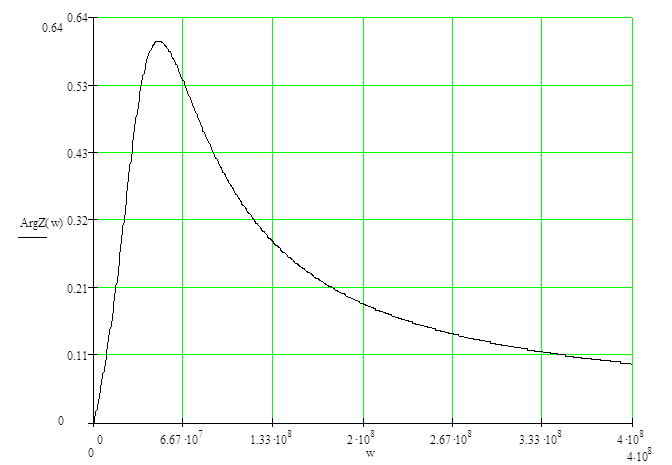
Рисунок 1.3 ‑ Зависимость аргумента от частоты; размерность ArgZ(w) – рад,
w – рад/с
2 РАСЧЁТ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ЦЕПИ
2.1 Определение комплексного коэффициента передачи цепи
Комплексный коэффициент передачи цепи:
| 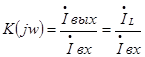
|
(9)
|
Предположим, входной ток есть, тогда:
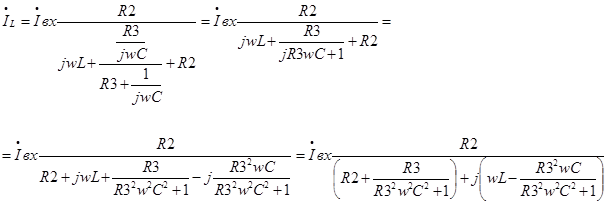 (10) (10)
Подставляя выражение (10) в (9) получим:
| 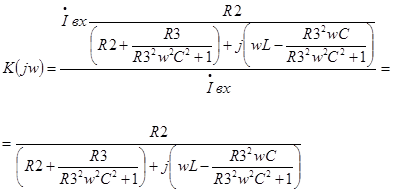
|
(11)
|
2.2 Определение амплитудно-частотной характеристики цепи
Амплитудно-частотная характеристика (АЧХ):
| 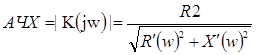 , ,
|
(12)
|
где:
 (13), а (13), а 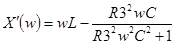 (14) (14)
Подставляя числовые значения в выражения (13) и (14), а затем в (12) получим:
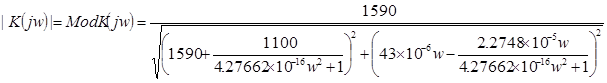 (15) (15)
Результаты расчётов приведены в таблице 2.1, а кривая, построенная на основании результатов, имеет вид графика изображённого на рисунке 2.1
| Таблица 2.1
|
Зависимость ModK(jw) от частоты
|
| w, рад/с
|
ModK(jw)
|
| 0
|
0.5910781
|
| 1*10^7
|
0.5992408
|
| 2*10^7
|
0.6179827
|
| 3*10^7
|
0.6324491
|
| 4*10^7
|
0.6273599
|
| 5*10^7
|
0.5983093
|
| 7*10^7
|
0.5024911
|
| 8*10^7
|
0.4538942
|
| 9*10^7
|
0.4104007
|
| 1*10^8
|
0.3726731
|
| 1.1*10^8
|
0.3403078
|
| 1.3*10^8
|
0.2887096
|
| 1.4*10^8
|
0.2680577
|
| 1.5*10^8
|
0.2500606
|
| 1.6*10^8
|
0.2342674
|
| 1.7*10^8
|
0.2203143
|
| 1.9*10^8
|
0.1968111
|
| 2*10^8
|
0.186831
|
| 2.1*10^8
|
0.1778097
|
| 2.2*10^8
|
0.169617
|
| 2.3*10^8
|
0.1621448
|
| 2.4*10^8
|
0.1553027
|
| 2.5*10^8
|
0.1490146
|
| 2.7*10^8
|
0.1378528
|
| 2.8*10^8
|
0.132877
|
| 3*10^8
|
0.1239321
|
| 3.1*10^8
|
0.1198974
|
| 3.2*10^8
|
0.1161177
|
| 3.3*10^8
|
0.1125694
|
| 3.4*10^8
|
0.109232
|
| 3.5*10^8
|
0.1060873
|
| 3.6*10^8
|
0.1031189
|
| 3.8*10^8
|
0.097655
|
| 3.9*10^8
|
0.0951351
|
| 4*10^8
|
0.0927421
|
| 4.1*10^8
|
0.0904669
|
| 4.2*10^8
|
0.0883008
|
| 4.3*10^8
|
0.0862362
|
| 4.4*10^8
|
0.0842662
|
| 4.6*10^8
|
0.0805848
|
| 4.7*10^8
|
0.0788623
|
| 4.8*10^8
|
0.0772121
|
| 4.9*10^8
|
0.0756296
|
| 5*10^8
|
0.0741108
|
| 5.1*10^8
|
0.0726519
|
| 5.2*10^8
|
0.0712494
|
| 5.4*10^8
|
0.0686011
|
| 5.5*10^8
|
0.0673495
|
| 5.6*10^8
|
0.0661428
|
| 5.7*10^8
|
0.0649787
|
| 5.8*10^8
|
0.0638548
|
| 5.9*10^8
|
0.0627693
|
| 6*10^8
|
0.0617201
|
| 
|
0
|
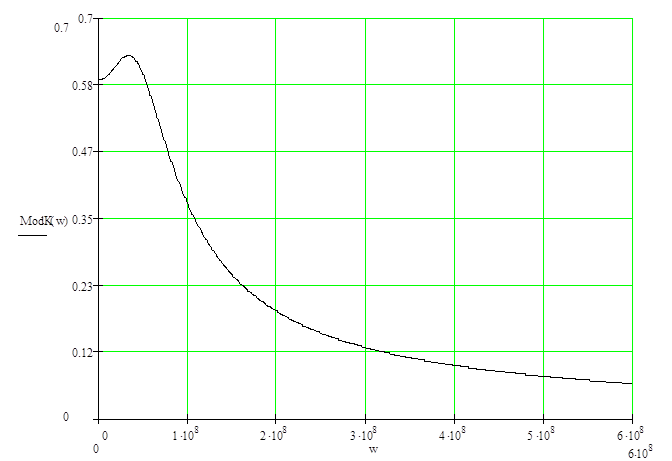
Рисунок 2.1 ‑ АЧХ цепи; размерность w – рад/с, ModK(w) – безразмерная величина
2.3 Определение фазочастотной характеристики цепи
Фазочастотная характеристика цепи (ФЧХ):
| 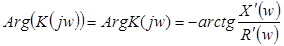
|
(16)
|
Подставляя числовые значения в (16) получим:
| 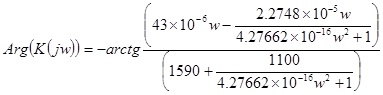
|
(17)
|
Результаты расчётов приведены в таблице 2.2, а кривая, построенная на основании результатов, имеет вид графика изображённого на рисунке 2.2
| Таблица 2.2
|
Зависимость ArgK(jw) от частоты
|
| w, рад/с
|
ArgK(jw), рад
|
| 0
|
0
|
| 1*10^7
|
-0.0799271
|
| 3*10^7
|
-0.3226808
|
| 5*10^7
|
-0.6462386
|
| 7*10^7
|
-0.9086729
|
| 9*10^7
|
-1.0769648
|
| 1.1*10^8
|
-1.1826898
|
| 1.3*10^8
|
-1.2524606
|
| 1.5*10^8
|
-1.3011954
|
| 1.7*10^8
|
-1.3369474
|
| 1.9*10^8
|
-1.3642366
|
| 2.1*10^8
|
-1.3857381
|
| 2.3*10^8
|
-1.4031184
|
| 2.5*10^8
|
-1.4174637
|
| 2.7*10^8
|
-1.42951
|
| 2.9*10^8
|
-1.4397731
|
| 3.1*10^8
|
-1.4486249
|
| 3.3*10^8
|
-1.4563401
|
| 3.5*10^8
|
-1.4631264
|
| 3.7*10^8
|
-1.4691435
|
| 3.9*10^8
|
-1.4745161
|
| 4.1*10^8
|
-1.4793434
|
| 4.3*10^8
|
-1.483705
|
| 4.6*10^8
|
-1.4895127
|
| 4.8*10^8
|
-1.492969
|
| 5*10^8
|
-1.4961411
|
| 5.2*10^8
|
-1.4990628
|
| 5.4*10^8
|
-1.5017629
|
| 5.6*10^8
|
-1.5042658
|
| 5.8*10^8
|
-1.5065924
|
| 6*10^8
|
-1.5087609
|
| 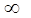
|
-1,5707963
|
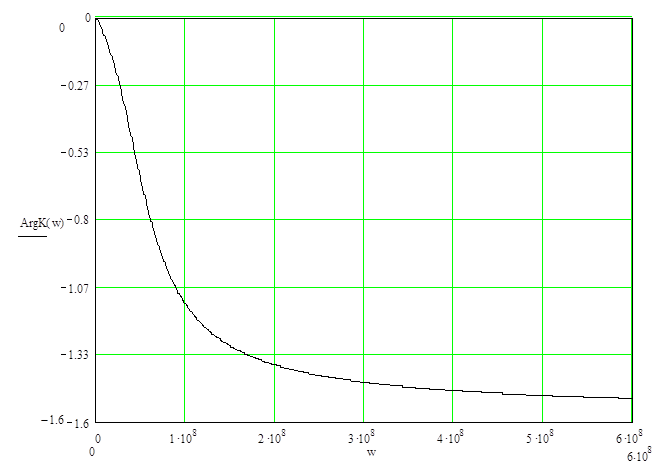
Рисунок 2.2 ‑ ФЧХ цепи; размерность ArgK(w) – рад, w – рад/с
3 РАСЧЕТ ВРЕМЕННЫХ ХАРАКТЕРИСТИК ЦЕПИ
3.1 Определение переходной характеристики цепи
Переходная характеристика цепи:
Т.к. воздействие – ток, а реакция – ток на индуктивности, следует (см. рисунок 3.1):
| 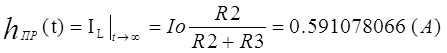 , ,
|
(19)
|
где Io – единичный скачок тока.
Для определения режима переходного процесса запишем входное сопротивление в операторной форме:
Рисунок 3.1‑Эквивалентная схема при t стремящемся к бесконечности
| 
|
(20)
|
Приравнивая знаменатель к нулю, после несложных преобразований получим:
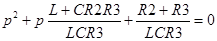 или или 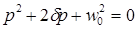 , ,
где:
| 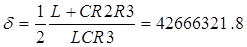 , ,
|
(21)
|
| 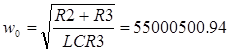 (рад/с) (рад/с)
|
(22)
|
Т.к. 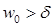 , следует режим колебательный, а значит: , следует режим колебательный, а значит:
|  , ,
|
(23)
|
| где:
 (рад/с) (рад/с)
|
(24)
|
– угловая частота затухающих свободных колебаний в контуре, А и 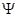 ‑ постоянные интегрирования. ‑ постоянные интегрирования.
Для определения постоянных интегрирования составим два уравнения для начальных значений 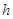 (+0) и (+0) и 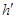 (+0): (+0):
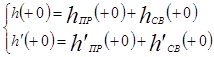 (25), (25), 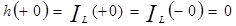 (26) (см. (26) (см.
рисунок 3.2),
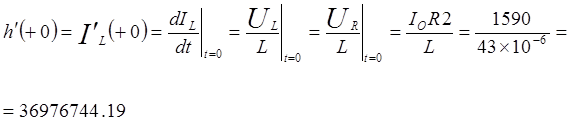 (27), (27),
т.к. в момент комутации напряжение на сопротивлении R2 равно напряжению на индуктивности (см. рисунок 3.2).
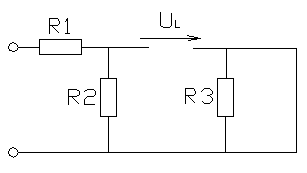
| 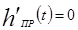
|
(28)
|
| 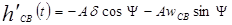
|
(29)
|
Рисунок 3.2 – Эквивалентная схема в момент коммутации
Подставляя выражения (19), (21), (23), (24), (26), (27), (28), (29) в (25) получим:
| 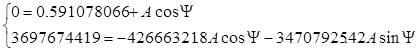
|
(30)
|

|
| 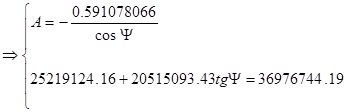
|
(31)
|
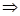
|
| 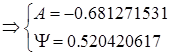
|
(32)
|
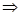
|
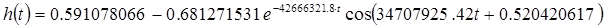 (33) (33)
Результаты расчётов приведены в таблице 3.1, а кривая, построенная на основании результатов, имеет вид графика изображённого на рисунке 3.3
| Таблица 3.1
|
Расчёт переходной характеристики
|
| t, с
|
h(t)
|
| 0
|
0
|
| 1.00e-8
|
0.303504193
|
| 2.00e-8
|
0.489869715
|
| 4.00e-8
|
0.632067650
|
| 5.00e-8
|
0.642131278
|
| 7.00e-8
|
0.624823543
|
| 8.00e-8
|
0.613243233
|
| 1.00e-7
|
0.597388596
|
| 1.10e-7
|
0.593357643
|
| 1.30e-7
|
0.590241988
|
| 1.40e-7
|
0.590004903
|
| 1.70e-7
|
0.590600383
|
| 1.90e-7
|
0.590939689
|
| 2.00e-7
|
0.591026845
|
| 2.20e-7
|
0.591095065
|
| 2.30e-7
|
0.591100606
|
| 2.50e-7
|
0.591093538
|
| 2.60e-7
|
0.591088357
|
| 2.80e-7
|
0.591081098
|
| 3.00e-7
|
0.591078184
|
| 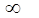
|
0.591078066
|
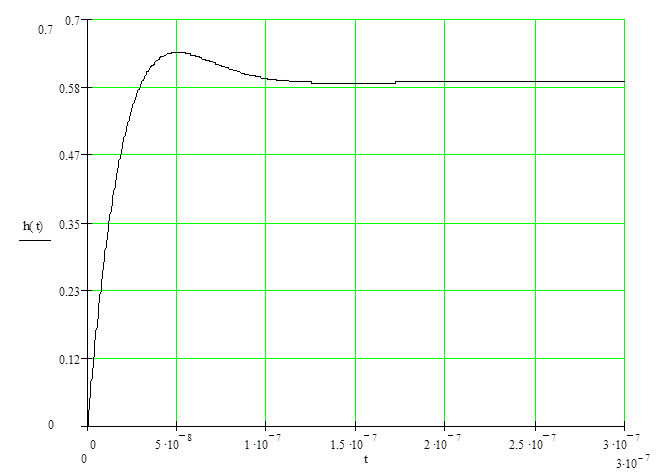
Рисунок 3.3 – Переходная характеристика цепи; размерность t – сек,
h(t) – безразмерная величина
Как видно из рисунка 3.3, свободные колебания затухают достаточно быстро; при таком масштабе рисунка видны колебания в течение, примерно, одного периода свободных колебаний (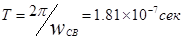 ), однако переходной процесс длится немного дольше, а спустя 0,3 мкс колебаниями можно пренебречь т.к. они достаточно малы (см. таблицу 3.1) и считать переходной процесс завершенным. ), однако переходной процесс длится немного дольше, а спустя 0,3 мкс колебаниями можно пренебречь т.к. они достаточно малы (см. таблицу 3.1) и считать переходной процесс завершенным.
3.2 Определение импульсной характеристики цепи
Импульсная характеристики цепи:
| 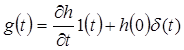
|
(34),
|
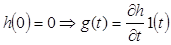
|
(35),
|
где 1(t) – единичная функция.
Подставляя (33) в (35) находим:
| 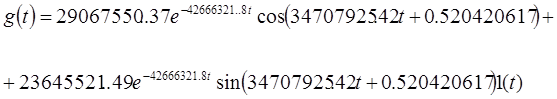
|
(36)
|
Результаты расчётов приведены в таблице 3.2, а кривая, построенная на основании результатов, имеет вид графика изображённого на рисунке 3.4 и 3.5

Рисунок 3.4 – Импульсная характеристика цепи в крупном масштабе; размерность t – сек, g(t) – безразмерная величина
Оба графика имеют одну и ту же шкалу времени, поэтому можно оценить, насколько быстро затухают колебания, и во сколько раз уменьшается их амплитуда за ничтожный промежуток времени.
| Таблица 3.2
|
Расчёт импульсной характеристики
|
| t, c
|
g(t)
|
| 0
|
3.697e7
|
| 4.0e-8
|
2.299e6
|
| 6.0e-8
|
-9.911e5
|
| 8.0e-8
|
-1.066e6
|
| 1.0e-7
|
-5.184e5
|
| 1.2e-7
|
-1.460e5
|
| 1.4e-7
|
-1.503e3
|
| 1.8e-7
|
1.697e4
|
| 2.0e-7
|
6.486e3
|
| 2.2e-7
|
1.167e3
|
| 2.4e-7
|
-412.634
|
| 2.6e-7
|
-482.050
|
| 2.8e-7
|
-240.781
|
| 3.0e-7
|
-70.193
|
| 3.2e-7
|
-2.270
|
| 3.6e-7
|
7.780
|
| 3.8e-7
|
3.053
|
| 4.0e-7
|
0.587
|
| 4.2e-7
|
-0.169
|
| 4.4e-7
|
-0.218
|
| 4.6e-7
|
-0.112
|
| 4.8e-7
|
-0.034
|
| 5.0e-7
|
-1.775e-3
|
| 5.4e-7
|
3.561e-3
|
| 5.6e-7
|
1.434e-3
|
| 5.8e-7
|
2.930e-4
|
| 6.0e-7
|
-6.843e-5
|
| 6.2e-7
|
-9.799e-5
|
| 6.4e-7
|
-5.175e-5
|
| 6.6e-7
|
-1.610e-5
|
| 7.0e-7
|
2.166e-6
|
| 7.4e-7
|
6.730e-7
|
| 7.6e-7
|
1.453e-7
|
| 7.8e-7
|
-2.702e-8
|
| 8.0e-7
|
-4.405e-8
|
| 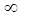
|
0
|
Рисунок 3.5 – Импульсная характеристика в более мелком масштабе
; размерность t – сек, g(t) – безразмерная величина
3.3 Расчет отклика цепи на заданное воздействие методом интеграла Дюамеля
При кусочно-непрерывной форме воздействия отклик необходимо искать для каждого из интервалов времени отдельно.
При применении интеграла Дюамеля с использованием переходной характеристики h(t) отклик:
при 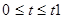
| 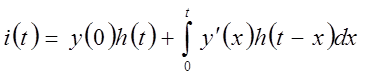 , ,
|
(37)
|
где:
y(x) – аналитическое выражение описывающее воздействие (см. рисунок 3.6)
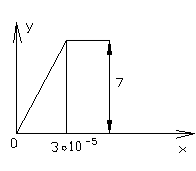
составим аналитическое выражение y(x):
| 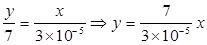
|
(38)
|
| Рисунок 3.6 – График воздействия
|
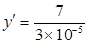
|
(39)
|
Подставляя выражения (33), (39) в(37) и учитывая, что y(0)=0 получим:

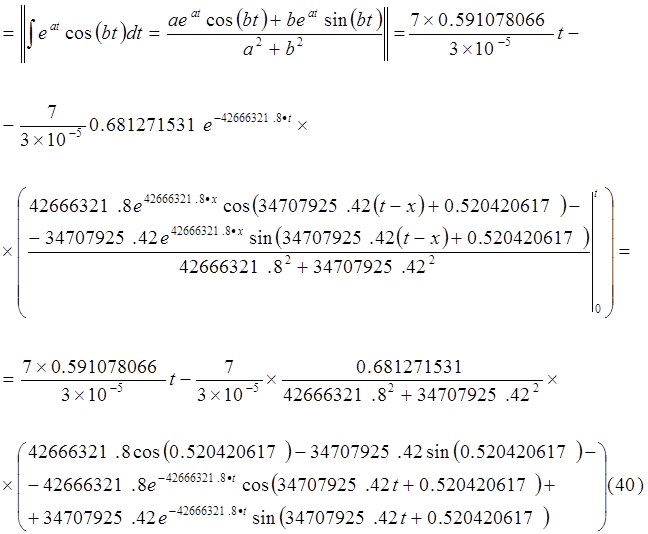
Результаты расчётов приведены в таблице 3.3, а кривая, построенная на основании результатов, имеет вид графика изображённого на рисунке 3.7 и 3.8
| Таблица 3.3
|
Расчёт отклика при 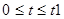
|
| t, c
|
i(t), А
|
| 0
|
0
|
| 1.0e-6
|
0.136879881
|
| 2.0e-6
|
0.274798097
|
| 3.0e-6
|
0.412716312
|
| 5.0e-6
|
0.688552743
|
| 6.0e-6
|
0.826470958
|
| 7.0e-6
|
0.964389174
|
| 9.0e-6
|
1.240225604
|
| 1.0e-5
|
1.378143820
|
| 1.1e-5
|
1.516062035
|
| 1.3e-5
|
1.791898466
|
| 1.4e-5
|
1.929816681
|
| 1.5e-5
|
2.067734897
|
| 1.7e-5
|
2.343571328
|
| 1.8e-5
|
2.481489543
|
| 1.9e-5
|
2.619407758
|
| 2.1e-5
|
2.895244189
|
| 2.2e-5
|
3.033162405
|
| 2.3e-5
|
3.171080620
|
| 2.5e-5
|
3.446917051
|
| 2.6e-5
|
3.584835266
|
| 2.7e-5
|
3.722753482
|
| 2.8e-5
|
3.860671697
|
| 2.9e-5
|
3.998589912
|
| 3.0e-5
|
4.136508126
|
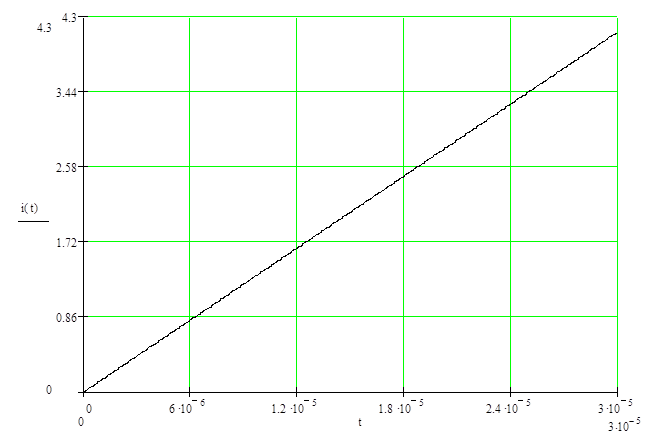
Рисунок 3.7 – Отклик цепи при 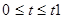 в крупном масштабе; размерность в крупном масштабе; размерность
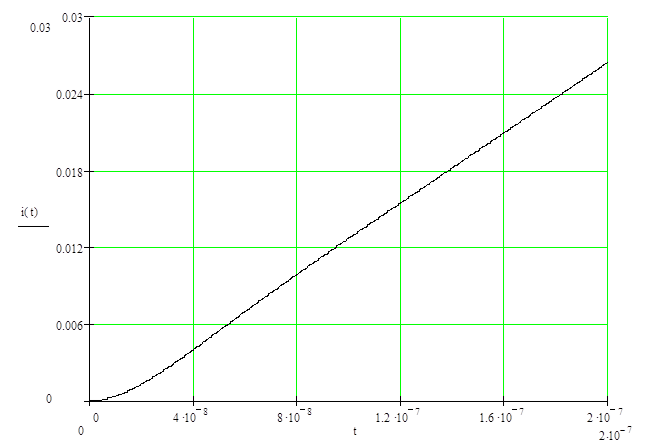
t – сек, i(t) – Ампер
Рисунок 3.8 ‑ Отклик цепи при 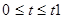 в более мелком масштабе; размерность в более мелком масштабе; размерность
t – сек, i(t) – Ампер
Поскольку данный график содержит ось времени от 0 до t1, да плюс, как мы увидели по переходной характеристике, затухание происходит очень быстро, увидеть в таком масштабе колебания нельзя. На рисунке 3.8 ось времени содержит значения от 0 и до 2*10^-7 секунд, на этом графике хоть и слабо, но все же видно, что нарастание вначале нелинейное.
при 
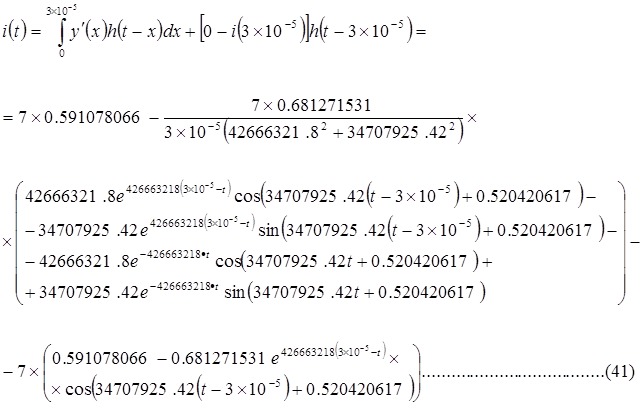
Результаты расчётов приведены в таблице 3.4, а кривая, построенная на основании результатов, имеет вид графика изображённого на рисунке 3.9
| Таблица 3.4
|
Расчёт отклика при 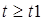
|
| t, c
|
i(t), А
|
| 3.e-5
|
4.136508126
|
| 3.001e-5
|
2.012978646
|
| 3.002e-5
|
0.708853559
|
| 3.004e-5
|
-0.286479932
|
| 3.006e-5
|
-0.316233940
|
| 3.007e-5
|
-0.236089753
|
| 3.009e-5
|
-0.089807225
|
| 3.010e-5
|
-0.044172156
|
| 3.011e-5
|
-0.015965080
|
| 3.012e-5
|
-7.804401718e-4
|
| 3.015e-5
|
6.723438063e-3
|
| 3.016e-5
|
5.056128946e-3
|
| 3.017e-5
|
3.342384970e-3
|
| 3.019e-5
|
9.685895329e-4
|
| 3.020e-5
|
3.587128387e-4
|
| 3.022e-5
|
-1.187888560e-4
|
| 3.024e-5
|
-1.428833579e-4
|
| 3.025e-5
|
-1.082465352e-4
|
| 3.026e-5
|
-7.200797423e-5
|
| 3.028e-5
|
-2.122389760e-5
|
| 3.029e-5
|
-8.042151551e-6
|
| 3.030e-5
|
-8.306802357e-7
|
| 
|
0
|
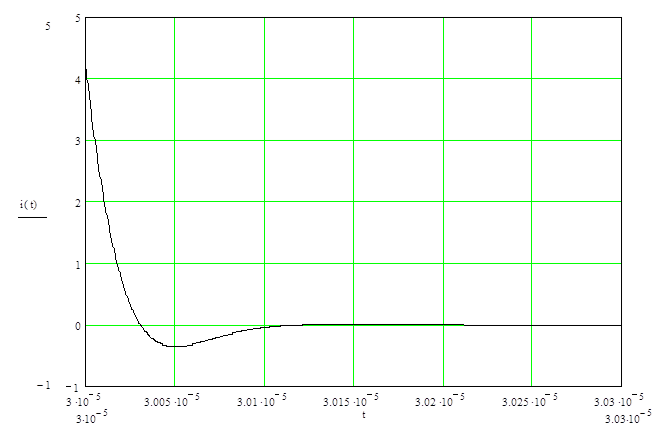
Рисунок 3.9 – Отклик цепи при 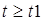 ; размерность t – сек, i(t) – Ампер ; размерность t – сек, i(t) – Ампер

Таким образом, отклик на заданное воздействие имеет вид графика изображенного на рисунке 3.10
Рисунок 3.10 – Отклик цепи; размерность t – сек, i(t) ‑ Ампер
ВЫВОДЫ
В процессе выполнения курсовой работы вопросов появляется больше, чем пунктов в задании. Одними из них является семейство вопросов о размерности коэффициентов и промежуточных величин при расчете переходной характеристики, а также размерность ее производной и т.д.
В план закрепления материала, на мой взгляд, идут только первые четыре задания, поскольку с такого рода задачами мы встречались, а последние три задания представляют особую важность, их приходится не закреплять – в них приходится разбираться.
Достоинством данной курсовой работы является подбор в ней заданий, они не являются нудными и однообразными как, например, курсовые по механике, в которых все одно и тоже и в пять раз больше.
СПИСОК ИСПОЛЬЗОВАНЫХ ИСТОЧНИКОВ
1. В. П. Шинкаренко, П. Ф. Лебедев. Методические указания к курсовой работе по курсу « Теория электрических и магнитных цепей». ‑ Харьков: «ХГТУРЭ», 1993.
2. Т. А. Глазенко, В. А. Прянишников. Электротехника и основы электроники. – М.: «Высшая школа», 1985.
3. Г. И. Атабеков. Теоретические основы электротехники. – М.: «Энергия», 1978.
4. Н. В. Зернов, В. Г. Карпов. Теория радиотехнических цепей. – Л.: «Энергия», 1972.
|