Содержание
1. Введение……………………………………………………………………3
2. Постановка задачи…………………………………………………………4
3. Алгоритм имитации отжига………………………….……………………5
4. Общие схемы метода отжига……………………………………………...7
5. Анализ результатов……………………………………………………….12
6. Литература………………………………………………..……………….17
7. Приложение……………………………………………………………….18
Введение
Метод отжига – это техника оптимизации, использующая упорядоченный случайный поиск на основе аналогии с процессом образования веществом кристаллической структуры с минимальной энергией при охлаждении. В настоящее время метод отжига применяется для решения многих оптимизационных задач – финансовых, компьютерной графики, комбинаторных, в телекоммуникационных сетях, и многих других. Зачастую метод отжига используют для обучения нейронных сетей. Несмотря на такую широкую область применения, скорость сходимости метода отжига все еще мало изучена. История метода отжига начинается с 1953 года. В этом году Н. Метрополисом был разработан алгоритм симуляции установления равновесия в системе с множеством степеней свободы при заданной температуре. В начале 80-х у С. Киркпатрика впервые появилась идея использовать этот алгоритм не только для моделирования физических систем, но и для решения некоторых задач оптимизации. Огромным преимуществом метода отжига является свойство избежать “ловушки” в локальных минимумах оптимизируемой функции, и продолжить поиск глобального минимума. Это достигается за счет принятия не только изменений параметров, приводящих к уменьшению значения функции, но и некоторых изменений, увеличивающих ее значение, в зависимости от т.н. температуры характеристики моделируемого процесса. Чем выше температура, тем больше “ухудшающие” изменения допустимы, и больше их вероятность. Еще одним преимуществом является то, что даже в условиях нехватки вычислительных ресурсов для нахождения глобального минимума, метод отжига, как правило, выдает весьма неплохое решение. Л. Ингбером показано, что метод отжига и его модификации являются одним из наиболее эффективных методов случайного поиска оптимального решения для большого класса задач. К настоящему времени разработано множество различных вариантов метода отжига, как общих так и их специализаций для конкретных задач.
Реклама

Постановка задачи
Задача данной курсовой работы:
1. Применить алгоритм имитационной нормализации к решению оптимизационных задач. Применение рассматривается на примере решения задачи компоновки рюкзака: пусть имеется n
предметов, каждый из которых имеет ценность 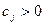 и объем и объем 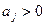 , , 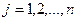 . Имеется ранец (рюкзак), объем которого есть V
, при этом . Имеется ранец (рюкзак), объем которого есть V
, при этом 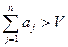 , то есть все предметы в ранец положить невозможно. Необходимо положить в ранец набор предметов с максимальной суммарной ценностью. , то есть все предметы в ранец положить невозможно. Необходимо положить в ранец набор предметов с максимальной суммарной ценностью.
2. Провести сравнительный анализ с другими подходами к решению оптимизационных задач.
Алгоритм имитации отжига
Алгоритм основывается на имитациифизического процесса, который происходит при кристаллизациивещества из жидкого состояния в твёрдое, в том числе при отжигеметаллов. Предполагается, что атомы уже выстроились в кристаллическую решётку, но ещё допустимы переходы отдельных атомов из одной ячейки в другую. Предполагается, что процесс протекает при постепенно понижающейся температуре. Переход атома из одной ячейки в другую происходит с некоторой вероятностью, причём вероятность уменьшается с понижением температуры. Устойчивая кристаллическая решётка соответствует минимумуэнергии атомов, поэтому атом либо переходит в состояние с меньшим уровнем энергии, либо остаётся на месте. (Этот алгоритм также называется алгоритмом Н. Метрополиса, по имени его автора).
При помощи моделирования такого процесса ищется такая точка или множество точек, на котором достигается минимум некоторой числовой функции 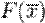 , где , где 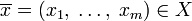 . Вводится последовательность точек . Вводится последовательность точек 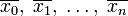 пространства X. Алгоритм последовательно находит следующую точку по предыдущей, начиная с точки пространства X. Алгоритм последовательно находит следующую точку по предыдущей, начиная с точки 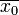 , которая является начальным приближением. Алгоритм останавливается по достижении точки , которая является начальным приближением. Алгоритм останавливается по достижении точки 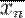 . .
Точка 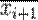 по алгоритму получается на основе текущей точки по алгоритму получается на основе текущей точки 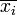 следующим образом. К точке следующим образом. К точке 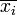 применяется оператор Α, который случайным образом модифицирует соответствующую точку, в результате чего получается новая точка применяется оператор Α, который случайным образом модифицирует соответствующую точку, в результате чего получается новая точка 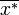 . Точка . Точка 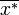 становится точкой становится точкой 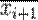 с вероятностью с вероятностью 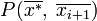 , которая вычисляется в соответствии с распределением Гиббса: , которая вычисляется в соответствии с распределением Гиббса:
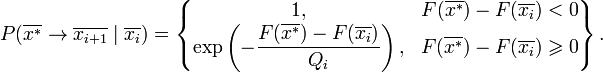
Здесь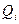 > 0 - элементы произвольной убывающей, сходящейся к нулю положительной последовательности, которая задаёт аналог падающей температуры в кристалле. Скорость убывания и закон убывания могут быть заданы по желанию создателя алгоритма.
> 0 - элементы произвольной убывающей, сходящейся к нулю положительной последовательности, которая задаёт аналог падающей температуры в кристалле. Скорость убывания и закон убывания могут быть заданы по желанию создателя алгоритма.
Алгоритм имитации отжига похож на градиентный спуск, но за счёт случайности выбора промежуточной точки должен будет попадать в локальные минимумы реже, чем градиентный спуск. Алгоритм имитации отжига не гарантирует нахождения минимума функции, однако при правильной политике генерации случайной точки в пространстве X, как правило, происходит улучшение начального приближения.
Реклама

Общие схемы метода отжига
Больцмановский отжиг
Исторически первой схемой метода отжига является схема Больцмановского отжига. Именно эта схема использовалась Н. Метрополисом для вычисления многомерных интегралов пути в задачах статистической физики, а также с Киркпатриком для решения задачи нахождения оптимальной разводки микросхем. В Больцмановском отжиге изменения температуры задается формулой 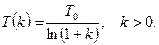
Семейство распределений 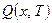 выбирается как семейство нормальных распределений с математическим ожиданием и дисперсией, т.е. задается плотностью выбирается как семейство нормальных распределений с математическим ожиданием и дисперсией, т.е. задается плотностью 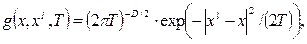
где D - размерность пространства состояний. Пространство состояний предполагается метрическим. Для Больцмановской схемы доказано, что при достаточно больших 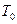 и общем количестве шагов k
, выбор такого семейства распределений гарантирует нахождение глобального минимума. и общем количестве шагов k
, выбор такого семейства распределений гарантирует нахождение глобального минимума.
Отжиг Коши (быстрый отжиг)
Основным недостатком Больцмановского отжига является очень медленное убывание температуры. Например, чтобы понизить исходную температуры в 40 раз, требуется 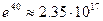 итераций, что уже вряд ли приемлемо при решении каких-либо задач. Ввиду этого Цу и Хартли предложили алгоритм, который позволяет использовать для изменения температуры схему итераций, что уже вряд ли приемлемо при решении каких-либо задач. Ввиду этого Цу и Хартли предложили алгоритм, который позволяет использовать для изменения температуры схему 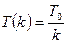 (1) без потери гарантии нахождения глобального минимума. Это достигается за счет использования в качестве Q
распределений Коши с плотностью (1) без потери гарантии нахождения глобального минимума. Это достигается за счет использования в качестве Q
распределений Коши с плотностью
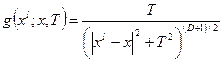
соответствующим образом нормированных. Например, в случае D
= 1 приходим к плотности
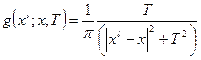 . .
К сожалению, это распределение не очень удобно моделировать в пространстве размерности больше 1. Этого можно избежать, например, с помощью перемножения D
одномерных распределений Коши:
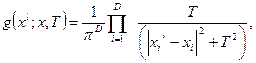
но в этом случае нахождении глобального минимума гарантируется только при законе изменения температуры не быстрее чем:
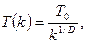 что гораздо медленнее схемы (1). что гораздо медленнее схемы (1).
Сверхбыстрый отжиг
Недостатки двух предыдущих методов привели к тому, что в 1989 году американским исследователем Л. Ингбером был разработан метод сверхбыстрого отжига. В нем пространство S
считается состоящим из D
-мерных векторов 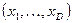 где где  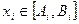 . Кроме этого, температура по каждой из координат может различаться, таким образом, T
также является вектором размерности D
. . Кроме этого, температура по каждой из координат может различаться, таким образом, T
также является вектором размерности D
.
Семейство распределений сроится следующим образом. Вводится функция
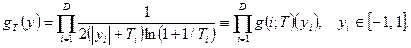
В качестве y
для получения плотности распределений 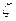 используется используется 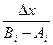 , таким образом, новое значение , таким образом, новое значение 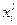 вычисляется по формуле вычисляется по формуле 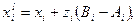 где где 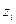 - случайная величина с плотностью - случайная величина с плотностью 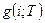 на на 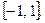
При этом выходящие за границы интервала значения параметра генерируются заново или приравниваются соответствующим границам. Такую случайную величину легко промоделировать:
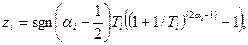 (2) (2)
где 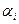 - независимые случайные величины, распределенные равномерно на - независимые случайные величины, распределенные равномерно на 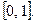
Доказано, что закон изменения температуры 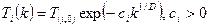 дает статистическую гарантию нахождения глобального минимума. Для вероятности принятия также используется отдельная шкала температуры, изменяющаяся по такому же закону. Как правило, при реализации этого метода дает статистическую гарантию нахождения глобального минимума. Для вероятности принятия также используется отдельная шкала температуры, изменяющаяся по такому же закону. Как правило, при реализации этого метода 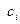 управляется двумя параметрами: управляется двумя параметрами: 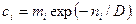
Преимущество такого методы очевидны. Во-первых, экспоненциальное убывание температуры гораздо быстрее достижимого в предыдущих методах. Во-вторых, разделение размерностей может дать большой выигрыш, как и благодаря отдельным температурам, так и благодаря ускорению процесса, в случае, если не нужно менять все координаты одновременно.
Кроме того, в отличие от отжига Коши, сверхбыстрый отжиг, как было показано, допускает очень быстрое моделирование распределения 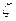 независимо от размерности S
. независимо от размерности S
.
Среди недостатков этого метода можно назвать то, что ввиду большого количества параметров иногда требуется несколько месяцев, чтобы хорошо настроить его для решения конкретной задачи.
Алгоритм Ксин Яо
Алгоритм Ксин Яо был повторным применением идеи предыдущего алгоритма. В качестве 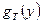 выбирается выбирается
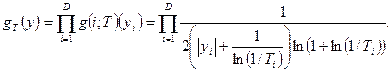
Утверждается, что при изменении температуры по закону
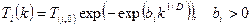
достигается статистическая гарантия нахождения глобального минимума.
Однако, как показано, увеличение скорости убывания температуры вовсе не означает ускорения в решении задачи. Более того, “размазанность” распределения приводит к тому, что метод генерирует огромное число “длинных” переходов, которые отвергаются в силу низкой вероятности их принятия.
Таким образом, несмотря на то. Что этот процесс итерировать до бесконечности, получая законы изменения температуры, ценность таких “улучшений” представляется сомнительной. Более того, легко видеть, что в пределе это приводит к тривиальному методу случайного поиска, которым является метод отжига при T
= 0.
Это в небольшой степени применимо и к методу сверхбыстрого отжига, так что вопрос о скорости сходимости этих методов, а также о других методах, обеспечивающих не такое быстрое убывание температуры, но большую скорость сходимости, остается открытым. Вполне возможны задачи, на которых вторая итерация вышеописанного процесса может давать не плохие результаты.
Метод
“
тушения
”
Далеко не всегда хватает вычислительных ресурсов на поиск глобального минимума. Кроме того, зачастую достаточно достигнуть не глобального оптимального решения задачи, а достаточно близкого к нему. Методы “тушения” не гарантируют нахождения глобального минимума, но, как правило, быстро находят близкое решение, а на практике зачастую и сам оптимум.
Основная идея этих методов заключается в том, чтобы скомбинировать семейство распределений 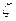 одного из предыдущих четырех методов с более быстрым законом убывания температуры. одного из предыдущих четырех методов с более быстрым законом убывания температуры.
Например, можно рассматривать нормальное распределение 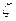 из Больцмановского отжига, но при этом уменьшать температуру по закону из Больцмановского отжига, но при этом уменьшать температуру по закону 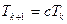 . .
Как правило, в этом случае c
выбирается между 0.7 и 0.99. Такой метод очень быстро сходится, и для конкретных задач может давать весьма неплохое решение, близкое к оптимальному, в условиях реального времени.
Зачастую они основаны либо на нормальном распределении, либо на распределении для сверхбыстрого отжига. Кроме того, встречаются специальные распределения, подобранные опытным путем для решения конкретных задач.
Анализ результатов
Программа была запущенна с разными исходными данными большое количество раз. Результаты эксперимента занесены в таблицу.
N– количество предметов; R– объём рюкзака.
| N |
R |
α |
Стоимость |
Вес предметов |
МДП |
МИО |
| 10 |
10 |
0,1 |
6 5 2 3 4 5 4 8 7 3 |
2 2 2 1 2 2 3 3 1 |
27/0,17с |
27/0,0156с |
| 20 |
10 |
0,1 |
6 5 2 3 4 5 4 8 7 3
6 5 2 3 4 5 4 8 7 3
|
2 2 2 1 2 2 3 3 1
2 2 2 1 2 2 3 3 1
|
29/0,18с |
29/0,0156с |
| 20 |
20 |
0,1
0,5
0,9
|
2 4 10 12 6 8 11 3 4 7 2 4 10 12 6 8 11 3 4 7 |
13 19 8 6 10 8 4 9 8 5 13 19 8 6 10 8 4 9 8 5 |
46/0,21с |
45/0,0156с
45/0,0572с
46/0,109с
|
| 30 |
20 |
0,1
0,5
0,9
|
2 9 1 10 5 7 1 12 3 4 2 9 1 10 5 7 1 12 3 4 2 9 1 10 5 7 1 12 3 4 |
5 6 2 3 7 2 5 12 5 2 2 3 7 2 5 2 5 12 5 2 2 3 7 2 5 6 8 7 3 3 |
66/0,23с |
64,7/0,014с
65,3/0,0218с
66/0,115с
|
| 40 |
10 |
0,1 |
6 5 2 3 4 5 4 8 7 3
6 5 2 3 4 5 4 8 7 3
6 5 2 3 4 5 4 8 7 3
6 5 2 3 4 5 4 8 7 3
|
2 2 2 1 2 2 3 3 1
2 2 2 1 2 2 3 3 1
2 2 2 1 2 2 3 3 1
2 2 2 1 2 2 3 3 1
|
30/0,23с |
30/0,0156 |
| 40 |
20 |
0,1
0,5
0,9
|
1 4 6 8 2 4 3 9 7 10 3 1 2 6 3 7 5 4 5 5 7 1 10 3 2 2 6 8 3 9 1 10 9 5 2 3 6 7 4 2 |
2 6 8 10 12 4 6 6 8 9 2 3 10 4 6 8 2 5 15 2 1 4 2 5 6 7 9 3 2 8 5 6 4 5 2 3 5 7 8 1 |
54/0,23с |
52/0,0156с
52/0,031с
52/0,468с
|
| 50 |
10 |
0,1
0,5
|
3 4 3 5 4 4 2 6 3 1 6 7 5 6 4 3 3 5 6 2 2 7 7 8 5 6 3 2 5 4 6 6 5 4 6 4 5 3 2 4 7 3 2 1 2 3 8 5 6 5 |
2 3 4 1 2 5 4 4 3 1 2 2 2 1 3 2 4 3 3 1 4 2 3 5 4 1 1 2 3 4 2 1 2 2 1 3 2 1 4 3 5 3 4 4 2 2 2 3 3 1 |
49/0,21с |
48,8/0,0652с
49/0,35с
|
| 50 |
20 |
0,1 |
1 4 6 8 2 4 3 9 7 10 3 1 2 6 3 7 5 4 5 5 7 1 10 3 2 2 6 8 3 9 1 10 9 5 2 3 6 7 4 2 1 4 6 8 2 4 3 9 7 10 |
2 6 8 10 12 4 6 6 8 9 2 3 10 4 6 8 2 5 15 2 1 4 2 5 6 7 9 3 2 8 5 6 4 5 2 3 5 7 8 1 1 8 7 5 3 2 5 4 6 5 |
57/0,24с |
57/0,125с |
50
50
|
20
30
|
0,1
0,5
0,9
0,1
|
4 5 4 4 6 3 7 6 5 6 8 7 7 8 6 5 7 3 4 5 6 6 5 4 7 6 6 5 7 4 5 5 6 3 4 5 8 7 6 5 5 6 7 6 5 4 4 5 3 4 |
5 10 2 5 7 12 9 5 2 2 7 1 1 8 2 13 1 1 8 5 6 9 3 1 7 4 8 10 2 9 1 3 1 5 5 5 3 12 5 6 3 2 2 10 11 5 4 7 10 9 |
79/0,23
98/0,21
|
77,8/0,0249с
78/0,0769с
78,8/0,503с
98/0,0156с
|
50
50
|
30
20
|
0,1
0,1
0,5
0,9
|
9 8 7 6 7 5 10 7 5 11 9 3 4 3 3 8 6 12 5 12 11 6 5 3 5 8 10 6 3 3 5 5 15 4 6 7 8 10 9 10 11 7 5 4 5 2 7 8 10 8 |
8 10 8 7 2 5 4 5 7 11 10 9 10 8 7 6 4 15 5 5 3 3 6 10 8 5 3 5 6 11 12 5 12 6 8 3 3 4 3 9 11 5 7 10 5 7 6 7 8 9 |
84/0,21с
59/0,21с
|
84/0,0262с
57/0,0512с
57,8/0,07с
58/0,61с
|
| 50 |
30 |
0,1 |
9 8 7 6 7 5 10 7 5 11 9 3 4 3 3 8 6 12 5 12 11 6 5 3 5 8 10 6 3 3 5 5 15 4 6 7 8 10 9 10 11 7 5 4 5 2 7 8 10 8 |
9 10 8 15 11 20 9 7 7 10 22 9 9 8 10 21 9 8 8 7 8 20 16 17 14 8 5 7 20 10 11 7 17 15 2 5 9 5 10 6 9 10 13 9 10 10 7 8 10 20 |
55/0,20с |
55/0,0124с |
| 50 |
50 |
0,1
0,5
0,9
|
3 4 3 5 4 4 2 6 3 1 6 7 5 6 4 3 3 5 6 2 2 7 7 8 5 6 3 2 5 4 6 6 5 4 6 4 5 3 2 4 7 3 2 1 2 3 8 5 6 5 |
25 21 20 30 21 19 31 32 20 15 23 20 15 23 20 15 21 33 33 21 18 34 20 15 22 16 34 25 20 14 15 30 21 19 31 20 23 15 23 20 14 21 15 30 21 34 18 20 15 16 14 22 25 |
21/0,21с |
18,5/0,017с
19/0,0311с
19,8/0,565с
|
| 50 |
50 |
0,1 |
3 4 3 5 4 4 2 6 3 1 6 7 5 6 4 3 3 5 6 2 2 7 7 8 5 6 3 2 5 4 6 6 5 4 6 4 5 3 2 4 7 3 2 1 2 3 8 5 6 5 |
25 3 20 15 5 23 30 35 6 2 2 29 31 7 31 8 25 3 2 2 30 33 24 20 19 10 15 35 7 1 2 33 34 25 20 21 25 22 2 33 31 15 10 11 10 5 3 30 31 5 |
66/0,20с |
66/0,0156с |
На основе данных, приведенных в таблицах, можно построить следующие графики.
Сравнение по среднему значению целевой функции
α = 0,9
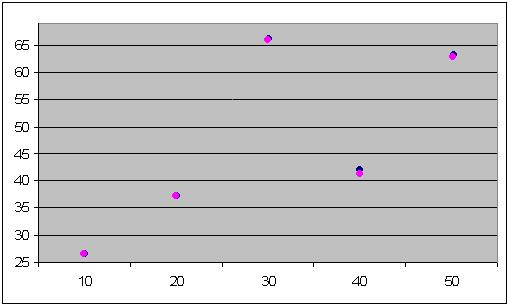
Сравнение по среднему времени работы программы
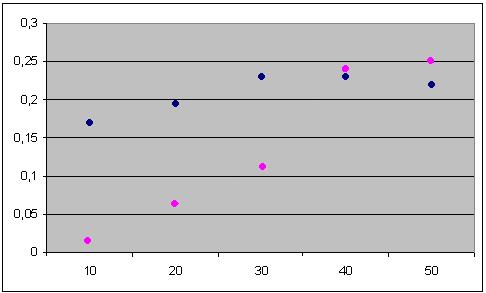
Сравнение по среднему значению целевой функции
α = 0,5
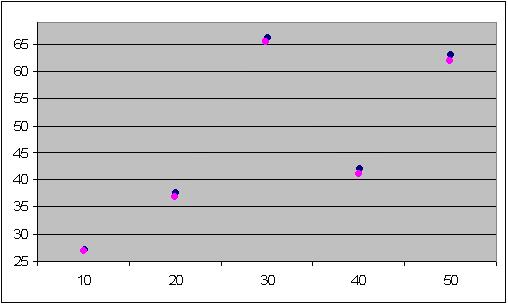
Сравнение по среднему времени работы программы
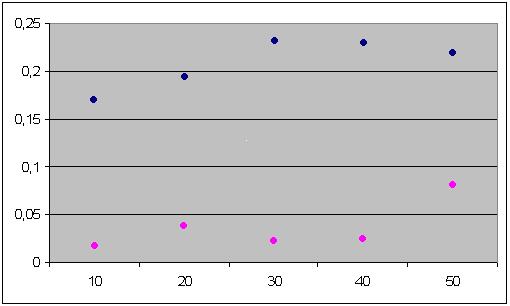
Сравнительный анализ работы алгоритмов
Для решения задачи компоновки рюкзака на плоскости использовались два алгоритма: имитации отжига и метод динамического программирования.
В результате тестирования программы были получены данные, представленные в таблице. По этим данным легко увидеть, что при α = 0,9 алгоритм имитации отжига дает оптимальное решение задачи или достаточно близкого к нему, но время выполнения программы превышает время выполнения метода динамического программирования при большом количестве предметов; при α = 0,5 алгоритм имитации отжига имеет наиболее высокую скорость нахождения решения по сравнению с метод динамического программирования и дает решение, близкое к оптимальному.
Литература
1. Лопатин А.С. Метод отжига: «http://www.math.spbu.ru/user/gran/sb1/lopatin.pdf»
2. Сигал И.Х., Иванова А.П. Введение в прикладное дискретное программирование: модели и вычислительные алгоритмы: Учеб. пособ. – Изд. 2-е, испр. – М.: ФИЗМАЛИТ, 2003. – 240 с.
3. Акулич И.Л., Математическое программирование в примерах и задачах. — М.: Высшая школа, 1986. — 319 с.
4. Габасов Р., Кириллова Ф. М. Основы динамического программирования. — Мн.: Изд-во БГУ, 1975. — 262 с.
Приложение
using System;
using System.Collections.Generic;
using System.Text;
namespace odgig
{
class rukzak
{
publicint[] x; // массивкник (хромосома)
privateint f;
publicdouble q;
public rukzak()
{
x = newint[Constants.N]; //выделяемпамятьдлямассивакниг
f = 0;// целевая функция
q = 0;
}
publicbool check()// проверка на допустимость
{
int sum = 0;
for (int i = 0; i < Constants.N; i++) sum += Program.a[i] * x[i];//сумма объемов предметов, положенных в рюкзак, фитнесс - функция
if (sum > Constants.R) returnfalse;// если сумма больше вместительности рюкзака,не допустимо
returntrue;
}
publicint g()//вычислениецелевойфункции
{
int sum = 0;
for (int i = 0; i < Constants.N; i++) sum += Program.c[i] * x[i];// формуладлявычисленияцелевойфункции
return sum;
}
publicint get_f()//обвертка
{
return f;
}
publicvoid set_f()//обвертка
{
f = g();
}
publicvoid copy(rukzak r)//функциякопирования
{
for (int i = 0; i < r.x.Length; i++) this.x[i] = r.x[i];
this.f = r.f;
}
publicvoid gadnyi()
{
elem[] ruk = new elem[Constants.N];
elem o = new elem();
for (int i = 0; i < Constants.N; i++) ruk[i] = new elem();
for (int i = 0; i < Constants.N; i++)
{
ruk[i].index = i;
}
for (int i = 0; i < Constants.N; i++)
{
if (Program.a[i] > 0)
ruk[i].averge = (double)(Convert.ToDouble(Program.c[i]) / Program.a[i]);
}
Array.Sort(ruk, new ElemMoreComparator());
for (int l = 0; l < Constants.N; l++)
{
this.x[ruk[l].index] = 1;
q = q + Program.a[ruk[l].index] * this.x[ruk[l].index];
if ((q < Constants.R) || (q == Constants.R)) f = f + Program.c[ruk[l].index] * this.x[ruk[l].index];
else
{
q = q - Convert.ToDouble(Program.a[ruk[l].index] * this.x[ruk[l].index]); this.x[ruk[l].index] = 0; break;
}
}
Console.Write("решение:(");
for (int l = 0; l < Constants.N; l++) Console.Write("{0}", this.x[l]);
Console.Write(")");
Console.WriteLine("целеваяфункция:{0}", f);
}
publicvoid Mutation(double Q)//мутация
{
rukzak mut = new rukzak();
mut.copy(this);
while (true)
{
for (int r = 0; r < 3; r++)
{
int border = (int)Program.myu(0, Constants.N - 1);//случайнымобразомвыбираемномермутирующейхромосомы
if (mut.x[border] == 0) mut.x[border] = 1;
else mut.x[border] = 0;
}
mut.set_f();
if (mut.check())
{
if (mut.get_f() > this.get_f())
{
this.copy(mut);
Console.WriteLine("целеваяф-ия:{0}", this.get_f());
break;
}
else
{
Constants.pMutation = Math.Exp(Convert.ToDouble(-(this.get_f() - mut.get_f()) / Q));
if (Program.myu(0, 1) < Constants.pMutation)
{
this.copy(mut);
Console.WriteLine("целеваяф-ия:{0}", this.get_f());
break;
}
else
{
mut.copy(this);
}
}
}
else mut.copy(this);
}
}
}
}
using System;
using System.Collections.Generic;
using System.Text;
using System.IO;
namespace odgig
{
class Program
{
staticpublicint[] c;
staticpublicint[] a;
staticpublicRandom rand = newRandom();
staticpublicdouble myu(double a, double b)
{
if (a > b)
{
Console.WriteLine("Первый параметр больше второго");
System.Environment.Exit(0);
}
double y = rand.NextDouble();
return (a + (b - a) * y);
}
staticvoid Main(string[] args)
{
StreamReader sReader = newStreamReader("inp.txt");
string[] str = sReader.ReadLine().Split(' ');
Constants.N = int.Parse(str[0]);
Constants.R = int.Parse(str[1]);
Program.c = newint[Constants.N];
Program.a = newint[Constants.N];
Console.Write("Цена:");
for (int j = 0; j <Constants.N; j++)
{
Program.c[j] = int.Parse(str[j + 2]);
Console.Write("{0} ", Program.c[j]);
}
Console.WriteLine();
Console.Write("Вес:");
for (int j = 0; j < Constants.N; j++)
{
Program.a[j] = int.Parse(str[j + Constants.N + 2]);
Console.Write("{0} ", Program.a[j]);
}
Console.WriteLine();
sReader.Close();
Console.WriteLine("Числопредметов:{0} Объемранца:{1}", Constants.N, Constants.R);
DateTime t1 = DateTime.Now;
rukzak gruk = new rukzak();
gruk.gadnyi();
double Q = 10;
while(true)
{
double a = 0.9;
Q = Q * a;
gruk.Mutation(Q);
DateTime t2 = DateTime.Now;
TimeSpan tProgram = t2 - t1;
if (Q < 0.5) Console.WriteLine("Время:" + Convert.ToString(tProgram));
}
}
}
}
using System;
using System.Collections.Generic;
using System.Text;
using System.Collections;
namespace odgig
{
class elem
{
publicdouble averge;
publicint index;
}
publicclass ElemMoreComparator : IComparer
{
privateconstdouble EPS = 1e-9;
#region IComparer Members
intIComparer.Compare(object x, object y)
{
elem e1 = (elem)x;
elem e2 = (elem)y;
double delta = e2.averge - e1.averge;
if (System.Math.Abs(delta) <=EPS)
return 0;
return System.Math.Sign(delta);
}
#endregion
}
}
|