СОДЕРЖАНИЕ
ВВЕДЕНИЕ……………………………………………………………………….3
ГЛАВА 1. ПОНЯТИЕ ЭКОНОМЕТРИКИ…………………………………...4
ГЛАВА 2. СУЩНОСТЬ И ПОСЛЕДСТВИЯ ГЕТЕРОСКЕДАСТИЧНОСТИ………………………………………………..6
ГЛАВА 3. ОБНАРУЖЕНИЕ ГЕТЕРОСКЕДАСТИЧНОСТИ……………..9
3.1. Тест ранговой корреляции Спирмена……………………………………9
3.2. Тест Голдфелда – Квандта…………………………………………………9
3.3. Тест Глейзера………………………………………………………………11
АНАЛИЗ ДАННЫХ ПО РАСХОДАМ НА ПРЕДМЕТ НАЛИЧИЯ ГЕТЕРОСКЕДАСТИЧНОСТИ………………………………………………12
ЗАКЛЮЧЕНИЕ………………………………………………………………...26
СПИСОК ЛИТЕРАТУРЫ…………………………………………………….27
ВВЕДЕНИЕ
При проведении регрессионного анализа определяются следующие этапы: определение коэффициентов корреляции и детерминации, средней ошибки отклонения и наилучшей модели, анализ данных на гетероскедастичность и автокорреляцию и т. д. На практике следует обратить серьезное внимание на проблемы, связанные с выполнимостью свойств случайных отклонений моделей. Свойства оценок коэффициентов регрессии напрямую зависят от свойств случайного члена в уравнении регрессии. Для получения качественных оценок необходимо следить за выполнимостью предпосылок МНК (условий Гаусса – Маркова), т. к. при их нарушении МНК может давать оценки с плохими статистическими свойствами. При этом существуют другие методы определения более точных оценок. Одной из ключевых предпосылок МНК является условие постоянства дисперсий случайных отклонений: дисперсия случайных отклонений  постоянна. постоянна.  для любых наблюдений i и j. для любых наблюдений i и j.
Выполнимость данной предпосылки называется гомоскедастичностью (постоянством дисперсии отклонений). Невыполнимость данной предпосылки называется гетероскедастичностью (непостоянством дисперсий отклонений).
В данной курсовой анализируется суть гетероскедастичности, ее причины и последствия, а также приводятся способы ее обнаружения.
ГЛАВА 1. ПОНЯТИЕ ЭКОНОМЕТРИКИ
Постоянно усложняющиеся экономические процессы потребовали создания и совершенствования особых методов изучения и анализа. Широкое распространение получило использование моделирования и количественного анализа. На этом этапе выделилось и сформировалось одно из направлений экономических исследований – эконометрика.
Эконометрика – это наука, в которой на базе реальных статистических данных строятся, анализируются и совершенствуются математические модели реальных экономических явлений. Эконометрика позволяет найти количественное подтверждение либо опровержение того или иного экономического закона либо гипотезы. Одним из важнейших направлений эконометрики является построение прогнозов по различным экономическим показателям.
Реклама

Эконометрика как научная дисциплина зародилась и получила развитие на основе слияния экономической теории, математической экономики, экономической и математической статистик.
Основные результаты экономической теории носят качественный характер, а эконометрика вносит в них эмпирическое содержание. Математическая экономика выражает экономические законы в виде математических соотношений, а эконометрика осуществляет опытную проверку этих законов. Экономическая статистика дает информационное обеспечение исследуемого процесса в виде исходных (обработанных) статистических данных и экономических показателей, а эконометрика, используя традиционные математико-статистические и специально разработанные методы, проводит анализ количественных взаимосвязей между этими показателями.
К основным задачам эконометрики можно отнести следующие:
· Построение эконометрических моделей, т. е. представление экономических моделей в математической форме, удобной для проведения эмпирического анализа.
· Оценка параметров построенной модели, делающих выбранную модель наиболее адекватной реальным данным.
· Проверка качества найденных параметров модели и самой модели в целом.
· Использование построенных моделей для объяснения поведения исследуемых экономических показателей, прогнозирования и предсказания, а также для осмысленного проведения экономической политики.
Развитие компьютерных систем и эконометрических пакетов, совершенствование методов анализа сделали эконометрику мощнейшим инструментом экономических исследований.
ГЛАВА 2. СУЩНОСТЬ И ПОСЛЕДСТВИЯ ГЕТЕРОСКЕДАСТИЧНОСТИ
При рассмотрении выборочных данных требование постоянства дисперсии случайных отклонений может вызвать определенное недоумение в силу того, что при каждом i-м наблюдении имеется единственное значение  . Откуда же появляется разброс? Дело в том, что при рассмотрении выборочных данных имеется дело с конкретными реализациями зависимой переменной . Откуда же появляется разброс? Дело в том, что при рассмотрении выборочных данных имеется дело с конкретными реализациями зависимой переменной  и соответственно с определенными случайными отклонениями и соответственно с определенными случайными отклонениями  Но до осуществления выборки эти показатели априори могли принимать произвольные значения на основе некоторых вероятностных распределений. Одним из требований к этим распределениям является равенство дисперсий. Данное условие подразумевает, что несмотря на то что при каждом конкретном наблюдении случайное отклонение может быть большим либо маленьким, положительным либо отрицательным, не должно быть некой априорной причины, вызывающей большую ошибку (отклонение) при одних наблюдениях и меньшую – при других. Но до осуществления выборки эти показатели априори могли принимать произвольные значения на основе некоторых вероятностных распределений. Одним из требований к этим распределениям является равенство дисперсий. Данное условие подразумевает, что несмотря на то что при каждом конкретном наблюдении случайное отклонение может быть большим либо маленьким, положительным либо отрицательным, не должно быть некой априорной причины, вызывающей большую ошибку (отклонение) при одних наблюдениях и меньшую – при других.
Реклама

Однако на практике гетероскедастичность не так уж и редка. Зачастую есть основания считать, что вероятностные распределения случайных отклонений  при различных наблюдениях будут различными. Это не означает, что случайные отклонения обязательно будут большими при определенных наблюдениях и малыми – при других, но это означает, что априорная вероятность этого велика. Поэтому важно понимать суть этого явления и его последствия. при различных наблюдениях будут различными. Это не означает, что случайные отклонения обязательно будут большими при определенных наблюдениях и малыми – при других, но это означает, что априорная вероятность этого велика. Поэтому важно понимать суть этого явления и его последствия.
Динамика изменения дисперсий (распределений) отклонений проиллюстрирована на рис. 1. При гомоскедастичности дисперсии εi
постоянны, а при гетероскедастичности дисперсии εi
изменяются (на данном рисунке – увеличиваются).

Рис. 1.
Проблема гетероскедастичности в большей степени характерна для перекрестных данных и довольно редко встречается при рассмотрении временных рядов. Это можно объяснить следующим образом. При перекрестных данных учитываются экономические субъекты (потребители, домохозяйства, фирмы, отрасли, страны и т. п.), имеющие различные доходы, размеры, потребности и т. д. Но в этом случае возможны проблемы, связанные с эффектом масштаба. Во временных рядах обычно рассматриваются одни и те же показатели в различные моменты времени (например, ВНП, чистый экспорт, темпы инфляции и т. д. в определенном регионе за определенный период времени). Однако при увеличении (уменьшении) рассматриваемых показателей с течением времени может возникнуть проблема гетероскедастичности.
При рассмотрении классической линейной регрессионной модели МНК дает наилучшие линейные несмещенные оценки лишь при выполнении ряда предпосылок, одной из которых является постоянство дисперсии отклонений (гомоскедастичность):  для всех наблюдений i, i = 1, 2,…, n. для всех наблюдений i, i = 1, 2,…, n.
При невыполнимости данной предпосылки (при гетероскедастичности) последствия применения МНК будут следующими:
1. Оценки коэффициентов по-прежнему остаются несмещенными и линейными.
2. Оценки не будут эффективными (т. е. они не будут иметь наименьшую дисперсию по сравнению с другими оценками данного параметра). Они не будут даже асимптотически эффективными. Увеличение дисперсии оценок снижает вероятность получения максимально точных оценок.
3. Дисперсии оценок будут рассчитываться со смещением.
4. Вследствие вышесказанного все выводы, получаемые на основе соответствующих t- и F-статистик, а также интервальные оценки будут ненадежными. Следовательно, статистические выводы, получаемые при стандартных проверках качества оценок, могут быть ошибочными и приводить к неверным заключениям по построенной модели. Вполне вероятно, что стандартные ошибки коэффициентов будут занижены, а следовательно, t-статистики будут завышены. Это может привести к признанию статистически значимыми коэффициентов, таковыми на самом деле не являющимися.
ГЛАВА 3. ОБНАРУЖЕНИЕ ГЕТЕРОСКЕДАСТИЧНОСТИ
3.1. Тест ранговой корреляции Спирмена
При использовании данного теста предполагается, что дисперсия отклонения будет либо увеличиваться, либо уменьшатся с увеличением значения X. Поэтому для регрессии, построенной по МНК, абсолютные величины отклонений  и значения и значения  будут коррелированы. Значения будут коррелированы. Значения  и и  ранжируются (упорядочиваются по величинам). Затем определяется коэффициент ранговой корреляции: ранжируются (упорядочиваются по величинам). Затем определяется коэффициент ранговой корреляции:

где  —
разность между рангами значений —
разность между рангами значений  и и  ( ( ). ).
Если соответствующий коэффициент корреляции для генеральной совокупности равен нулю, т. е. гетероскедастичность отсутствует, то коэффициент ранговой корреляции имеет нормальное распределение с математическим ожиданием 0 и дисперсией  . .
Соответствующая тестовая статистика равна:

Следовательно, если значение тестовой статистики, вычисленное по вышеприведенной формуле, превышает 1,96 и 2,58 при уровнях значимости в 5% и 1% соответственно (определяемое по таблице критических точек распределения Стьюдента), то необходимо отклонить гипотезу о равенстве нулю коэффициента корреляции, а следовательно, и об отсутствии гетероскедастичности. В противном случае гипотеза об отсутствии гетероскедастичности принимается.
3.2. Тест Голдфелда – Квандта
В данном случае предполагается, что стандартное отклонение  пропорционально значению пропорционально значению  переменной X в этом наблюдении. Предполагается, что переменной X в этом наблюдении. Предполагается, что  имеет нормальное распределение и отсутствует автокорреляция остатков. имеет нормальное распределение и отсутствует автокорреляция остатков.
Тест Голдфелда – Квандта состоит в следующем:
1. Все n наблюдений упорядочиваются по величине X по возрастающей.
2. Вся упорядоченная выборка после этого разбивается на две подвыборки размерностей k, (N – 2k), k соответственно.
3. Оцениваются отдельные регрессии для первой подвыборки (kпервых наблюдений) и для второй подвыборки (k последних наблюдений). Если предположение о пропорциональности дисперсий отклонений значениям X верно, то дисперсия регрессии (сумма квадратов остатков RSS1
) по первой подвыборке будет существенно меньше дисперсии регрессии (суммы квадратов остатков RSS2
) по второй подвыборке.
4. Для сравнения соответствующих дисперсий строится следующая F-статистика:

Здесь (k – m – 1) – число степеней свободы соответствующих выборочных дисперсий (m – количество объясняющих переменных в уравнении регрессии).
5. Если , то гипотеза об отсутствии гетероскедастичности отклоняется.
6. Если , то гипотеза об отсутствии гетероскедастичности принимается.
Естественным является вопрос, какими должны быть размеры подвыборок для принятия обоснованных решений. Для парной регрессии Голдфелд и Квандт предлагают следующие пропорции: n = 30, k = 11; n = 60, k = 22.
Этот же тест может быть использован при предположении об обратной пропорциональности между  и значениями объясняющей переменной. При этом F-статистика примет вид: (если X убывает). и значениями объясняющей переменной. При этом F-статистика примет вид: (если X убывает).
3.3. Тест Глейзера
Тест Глейзера предполагает анализ зависимостей между дисперсиями отклонений  и значениями переменной и значениями переменной  : :

В качестве зависимой переменной для изучения гетероскедастичности выбирается абсолютная величина остатков, т. е. осуществляется регрессия

где  – случайный член. – случайный член.
В качестве функций f обычно выбираются функции вида . Регрессия осуществляется при разных значениях γ, затем выбирается то значение, при котором коэффициент β оказывается наиболее значимым, т. е. имеет наибольшее значение t-статистики. Изменяя значения γ, можно построить различные регрессии. Обычно γ = …, -1, -0.5, 0, 0.5, 1, 1.5, … . Статистическая значимость коэффициента β в каждом конкретном случае фактически означает наличие гетероскедастичности. Если для нескольких регрессий коэффициент β оказывается статистически значимым, то при определении характера зависимости обычно ориентируются на лучшую из них.
АНАЛИЗ ДАННЫХ ПО РАСХОДАМ НА ПРЕДМЕТ НАЛИЧИЯ ГЕТЕРОСКЕДАСТИЧНОСТИ
Задача
Выполнить исследование по приведенным исходным данным, основанным на статистике США за годы с 1959-1983. Проанализировать данные на гетероскедастичность и автокорреляцию. Определить наилучшую модель из 3: линейной, степенной и гиперболической. Сделать выводы о модели.
Данные для расчета необходимо взять из табл. 1:
Таблица 1
| N |
Год |
Текущие расходы по газу (x) |
Совокупные личные расходы (y) |
| 1 |
1959 |
74,9 |
70,6 |
| 2 |
1960 |
79,8 |
71,9 |
| 3 |
1961 |
80,9 |
72,6 |
| 4 |
1962 |
80,8 |
73,7 |
| 5 |
1963 |
80,8 |
74,8 |
| 6 |
1964 |
81,1 |
75,9 |
| 7 |
1965 |
81,4 |
77,2 |
| 8 |
1966 |
81,9 |
79,4 |
| 9 |
1967 |
81,7 |
81,4 |
| 10 |
1968 |
82,5 |
84,6 |
| 11 |
1969 |
84 |
88,4 |
| 12 |
1970 |
88,6 |
92,5 |
| 13 |
1971 |
95 |
96,5 |
| 14 |
1972 |
100 |
100 |
| 15 |
1973 |
104,5 |
105,7 |
| 16 |
1974 |
117,7 |
116,3 |
| 17 |
1975 |
140,9 |
125,2 |
| 18 |
1976 |
164,8 |
131,7 |
| 19 |
1977 |
195,6 |
139,3 |
| 20 |
1978 |
214,9 |
149,1 |
| 21 |
1979 |
249,2 |
162,5 |
| 22 |
1980 |
297 |
179 |
| 23 |
1981 |
336,8 |
194,5 |
| 24 |
1982 |
404,2 |
206 |
| 25 |
1983 |
473,4 |
213,6 |
Решение:
1. Найдем линейную модель в виде  . Оценки для α и β определяем с помощью метода наименьших квадратов по формулам: . Оценки для α и β определяем с помощью метода наименьших квадратов по формулам:


Для этого найдем:
Среднее значение x:

Среднее значение y:

Ковариацию x и y:

Вариацию x:

Вариацию y:

Тогда,


Полученная мною линейная модель имеет вид:

В результате выполнения регрессионного анализа мною получено:
TSS –полная сумма квадратов:

RSS – остаточная сумма квадратов:

ESS – оцененная модель суммы квадратов:

Условия правильности моих вычислений на данном этапе проверим по формуле:
TSS = ESS + RSS
49901,17 = 46820,32 + 3080,849
Вычислим коэффициент корреляции и коэффициент детерминации:


Критерием правильности решения задачи является:

0,94 = 0,94
Данные параметры характеризуют хорошую линейную зависимость между текущими расходами и совокупными личными расходами на имеющихся статистических данных.
Найдем среднюю ошибку аппроксимации:

где 
Для наглядности представим результаты графически.

Примечание. Прямая линия – уравнение регрессии, а точки – статистические данные.
Определим доверительный интервал для параметров α и β:


Здесь  – квантиль t-распределения Стьюдента с (N – p) степенями свободы; p – число параметров, в моем случае он равен 2; – квантиль t-распределения Стьюдента с (N – p) степенями свободы; p – число параметров, в моем случае он равен 2;  и и  – оценки исследуемых параметров, полученные ранее с использованием метода наименьших квадратов; – оценки исследуемых параметров, полученные ранее с использованием метода наименьших квадратов;  и и  – несмещенные оценки для дисперсий случайных величин α и β; γ – уровень значимости. – несмещенные оценки для дисперсий случайных величин α и β; γ – уровень значимости.


Квантиль t–распределения Стьюдента с 23 степенями свободы находим из таблицы:
Для γ = 1%,  = 2,807 = 2,807
Для γ = 5%,  = 2,069 = 2,069
Доверительный интервал для 1% уровня значимости:
42,787 < α < 65,132
0,332 < β < 0,449
Доверительный интервал для 5% уровня значимости:
45,724 < α < 62,195
0,347 < β < 0,434
2. Для построения степенной модели вида необходимо привести ее к линейному виду с помощью следующего преобразования с использованием логарифмической функции: 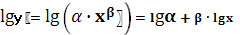 . Производя замены Y = lgy, X = lgx, A = lgα и B = β получим уравнение . Производя замены Y = lgy, X = lgx, A = lgα и B = β получим уравнение  , которое является уже линейным уравнением и его можно решить по аналогии с примером 1. , которое является уже линейным уравнением и его можно решить по аналогии с примером 1.
Вычислим параметры линейной регрессии:
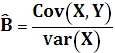

Для этого найдем:
Среднее значение X:
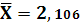
Среднее значение Y:
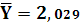
Ковариацию X и Y:
Вариацию X:
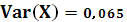
Вариацию Y:
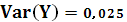
Тогда,
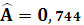
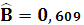
Уравнение линейной регрессии имеет вид:
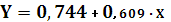 в логарифмах в логарифмах
Для дальнейшего анализа степенной функции необходимо выполнить обратное преобразование, то есть потенцирование полученного уравнения регрессии:

Определим:
TSS– полная сумма квадратов:
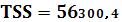
RSS – остаточная сумма квадратов:
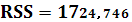
ESS – оцененная модель суммы квадратов:
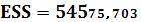
Вычислим коэффициент корреляции и коэффициент детерминации:
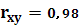
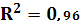
Критерием правильности решения задачи является:

0,96 = 0,96
Найдем среднюю ошибку аппроксимации:
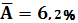
Определим доверительный интервал для параметров α и β:
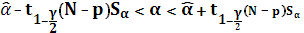
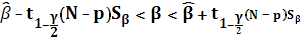
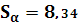
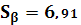
Квантиль t–распределения Стьюдента с 23 степенями свободы находим из таблицы:
Для γ = 1%,  = 2,807 = 2,807
Для γ = 5%,  = 2,069 = 2,069
Доверительный интервал для 1% уровня значимости:
-22,669 < α < 24,158
-18,812 < β < 20,031
Доверительный интервал для 5% уровня значимости:
-16,513 < α < 18,002
-13,706 < β < 14,925
3. Для построения гиперболической модели вида 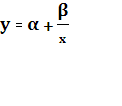 необходимо привести ее к линейному виду с помощью преобразования необходимо привести ее к линейному виду с помощью преобразования 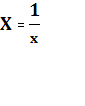 . Производя замены Y = y, X = . Производя замены Y = y, X =  , A = α и B = β получим уравнение , A = α и B = β получим уравнение  , которое является уже линейным уравнением и его можно решить по аналогии с примером 2. , которое является уже линейным уравнением и его можно решить по аналогии с примером 2.
Определяем параметры линейной регрессии:
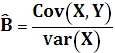

Для этого найдем:
Среднее значение X:
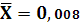
Среднее значение Y:
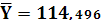
Ковариацию X и Y:
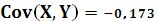
Вариацию X:
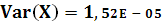
Вариацию Y:
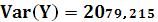
Тогда,
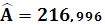
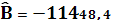
Уравнение линейной регрессии имеет вид:
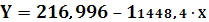
Для дальнейшего анализа гиперболической функции необходимо выполнить обратное преобразование, то есть:
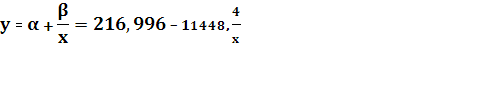
Определим:
TSS – полная сумма квадратов:
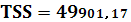
RSS – остаточная сумма квадратов:
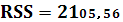
ESS – оцененная модель суммы квадратов:
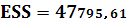
Вычислим коэффициент корреляции и коэффициент детерминации:
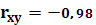

Критерием правильности решения задачи является:

0,96 = 0,96
Найдем среднюю ошибку аппроксимации:
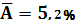
Определим доверительный интервал для параметров α и β:
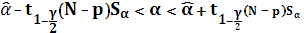
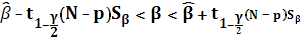
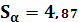
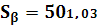
Квантиль t–распределения Стьюдента с 23 степенями свободы находим из таблицы:
Для γ = 1%, 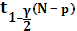 = 2,807 = 2,807
Для γ = 5%, 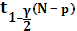 = 2,069 = 2,069
Доверительный интервал для 1% уровня значимости:
203,307 < α < 230,686
-12854,8 < β < -10042
Доверительный интервал для 5% уровня значимости:
206,906 < α < 227,087
-12485,1 < β < -10411,8
При определении средней ошибки аппроксимации, я получила, что у линейной функции  = 9,4%, у степенной функции = 9,4%, у степенной функции  = 6,2%, у гиперболической функции = 6,2%, у гиперболической функции  = 5,2%. Отсюда видно, что наименьшая средняя ошибка аппроксимации равняется = 5,2%. Отсюда видно, что наименьшая средняя ошибка аппроксимации равняется  = 5,2% у гиперболической функции, следовательно наилучшей моделью будет гиперболическая функция. = 5,2% у гиперболической функции, следовательно наилучшей моделью будет гиперболическая функция.
Тест ранговой корреляции Спирмена.
При проверке полученной модели на возможную гетероскедастичность данных воспользуемся тестом ранговой корреляции Спирмена. Значения  и и 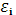 ранжируются (упорядочиваются по величинам). Определяем коэффициент ранговой корреляции: ранжируются (упорядочиваются по величинам). Определяем коэффициент ранговой корреляции:
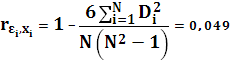
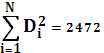
где 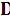 —
разность между рангами значений —
разность между рангами значений  и и 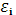 ( (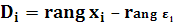 ); а ); а 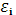 определяется по формуле определяется по формуле 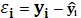 . .
Коэффициент ранговой корреляции имеет нормальное распределение с математическим ожиданием 0 и дисперсией . Тогда соответствующая тестовая статистика равна:
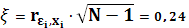
Нулевая гипотеза об отсутствии гетероскедастичности будет отклонена при уровне значимости в 5%, если ξ превысит 1,96, и при уровне значимости в 1%, если ξ превысит 2,58. Тестовая статистика составляет 0,24, что меньше, чем 1,96. Следовательно, нулевая гипотеза об отсутствии гетероскедастичности принимается. Этим я подтверждаю факт наличия у данных свойства гомоскедастичности.
Тест Голдфелда – Квандта.
Все n наблюдений упорядочиваются по величине X по возрастающей. Вся упорядоченная выборка после этого разбивается на две подвыборки размерностей k, (N – 2k). Оцениваются отдельные регрессии для первой подвыборки (k первых наблюдений) и для второй подвыборки (k последних наблюдений).
N = 25
k = 11
Для сравнения соответствующих дисперсий строится следующая F-статистика:
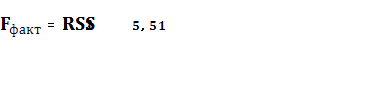
где сумма квадратов остатков RSS1
для первой подвыборки: RSS1
= 428,699; сумма квадратов остатков RSS2
для второй подвыборки: RSS2
= 2361,268.
Fтабл
(1%) = 7,88
Fтабл
(5%) = 4,28
Так как , то данные гомоскедастичны.
Критерий Дарбина – Уотсона.

В моем случае d будет меньше dкр
. Вывод: наличие положительной автокорреляции.
d < dкр
(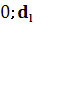 ) )
Для d-статистики найдены верхняя 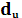 и нижняя и нижняя 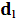 границы: границы:
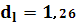
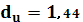
Т. к. статистика Дарбина – Уотсона ниже интервала, то существует положительная автокорреляция.
Процедура Кохрейна – Оркатта.
Указанная процедура заключается в том, чтобы получить оценочное значение параметра 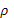 . Далее применяют метод наименьших квадратов к регрессионному уравнению. . Далее применяют метод наименьших квадратов к регрессионному уравнению.
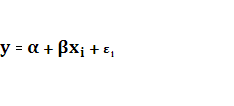 – линейная модель наблюдения – линейная модель наблюдения
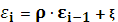
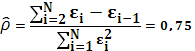
Сделаем замену:
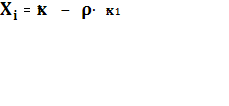
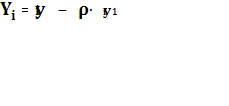
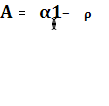

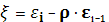
Получаем новую модель наблюдения:
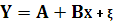
С каждой процедурой наши значения уменьшаются на одно значение (в данной задаче 25 значений, после первой попытки избавиться от автокорреляции у нас стало 24 значения, а со второй попытки уже 23). Эта процедура повторяется вновь и вновь, до тех пор, пока не избавимся от автокорреляции.
В ходе решения были получены:
Среднее значение x:
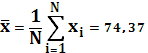
Среднее значение y:
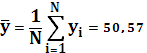
Ковариацию x и y:
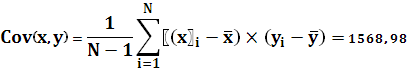
Вариацию x:
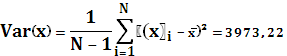
Вариацию y:
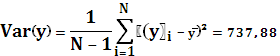
Оценки параметров α и β:
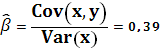
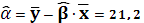
TSS –полная сумма квадратов:
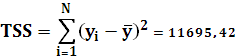
RSS – остаточная сумма квадратов:
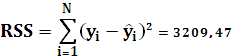
ESS – оцененная модель суммы квадратов:
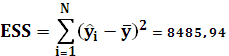
Вычислим коэффициент корреляции и коэффициент детерминации:
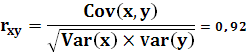
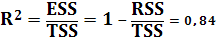
Найдем среднюю ошибку аппроксимации:
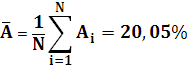
Статистика Дарбина – Уотсона:
d = 0,084
Границы d-статистики:
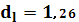
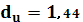
Т. к. статистика Дарбина – Уотсона ниже интервала, то существует положительная автокорреляция.
Данный метод продемонстрировал опасность пренебрежения возможной неадекватностью построенной модели в отношении стандартных предположений об ошибках и необходимость обязательного проведения в процессе подбора подходящей модели связи между теми или иными экономическими факторами анализа ошибок (остатков), полученных при оценивании выбранной модели.
ЗАКЛЮЧЕНИЕ
В ряде случаев на базе знаний характера данных появление проблемы гетероскедастичности можно предвидеть и попытаться устранить этот недостаток еще на этапе спецификации. Однако значительно чаще эту проблему приходится решать после построения уравнения регрессии.
Обнаружение гетероскедастичности в каждом конкретном случае является довольно сложной задачей, т. к. для знания дисперсий отклонений σ2
(εi
) необходимо знать распределение Y, соответствующее выбранному значению xi
. На практике зачастую для каждого конкретного значения xi
определяется единственное значение yi
, что не позволяет оценить дисперсию Y для данного xi
.
В заключение отметим, что наличие гетероскедастичности не позволяет получить эффективные оценки, что зачастую приводит к необоснованным выводам по их качеству. Обнаружение гетероскедастичности – достаточно трудоемкая проблема и для ее решения разработано несколько методов.
Все они используют в качестве нулевой гипотезы H0
гипотезу об отсутствии гетероскедастичности.
В ходе исследований я получила, что наилучшей моделью является гиперболическая функция, т. к. ей соответствует наименьшая средняя ошибка аппроксимации равная  = 5,2%. При проверке полученной модели на возможную гетероскедастичность данных я воспользовалась тестом ранговой корреляции Спирмена и тестом Голдфелда – Квандта. В результате обоих вычислений нулевая гипотеза об отсутствии гетероскедастичности принимается, следовательно мои данные гомоскедастичны. = 5,2%. При проверке полученной модели на возможную гетероскедастичность данных я воспользовалась тестом ранговой корреляции Спирмена и тестом Голдфелда – Квандта. В результате обоих вычислений нулевая гипотеза об отсутствии гетероскедастичности принимается, следовательно мои данные гомоскедастичны.
СПИСОК ЛИТЕРАТУРЫ
1. Бородич С.А. Эконометрика. – Мн.: Новое знание, 2004.
2. Доугерти К. Введение в эконометрику. – М.: ИНФРА-М, 1999.
3. Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов. – М.: ЮНИТИ, 2002.
4. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс. – М.: Дело, 2004.
5. Орлов А.И. Эконометрика. – М.: Экзамен, 2002.
6. Суслов В.И., Ибрагимов Н.М., Талышева Л.П. Эконометрия. – Новосибирск.: СО РАН, 2005.
7. Харин Ю.С., Малюгин В.И., Харин А.Ю. Эконометрическое моделирование. – Мн.: БГУ, 2003.
|