| Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
Вятский государственный гуманитарный университет
Математический факультет
Кафедра алгебры и геометрии
Выпускная квалификационная работа
Топологическая определяемость верхних полурешёток.
Выполнил:
студент V курса математического факультета
Малых Константин Леонидович
Научный руководитель:
кандидат физико-математических наук, доцент кафедры алгебры и геометрии В.В. Чермных
Рецензент:
доктор физико-математических наук, профессор, заведующий кафедрой алгебры и геометрии Е.М. Вечтомов
Допущена к защите в государственной аттестационной комиссии
«___» __________2005 г. Зав. Кафедрой Е.М. Вечтомов
«___»___________2005 г. Декан факультета В.И. Варанкина
Киров 2005
Оглавление.
Введение …………………………………………………………………стр. 3
Глава 1 ……………………………………………………………………стр. 4
1. Упорядоченные множества ………………………………………стр. 4
2. Решётки.……………………………………………………………стр. 5
3. Дистрибутивные решётки ………………………………………..стр. 8
4. Топологические пространства……………………………………стр.10
Глава 2…………………………………………………………………….стр.11
1. Верхние полурешётки…………………………………………….стр.11
2. Стоуново пространство …………………………………………..стр.15
Список литературы……………………………………………………….стр.21
Введение.
Дистрибутивная решётка является одним из основных алгебраических объектов. В данной работе рассматривается частично упорядоченное множество P
(
L
)
простых идеалов. Оно даёт нам много информации о дистрибутивной решётке L
,
но оно не может её полностью охарактеризовать. Поэтому, для того, чтобы множество P
(
L
)
характеризовало решётку L
,
необходимо наделить его более сложной структурой. Стоун [1937] задал на множестве P
(
L
)
топологию.
В этой работе рассматривается этот метод в несколько более общем виде.
Работа состоит из двух глав. В первой главе вводятся начальные понятия, необходимые для изучения данной темы. Во второй главе рассматриваются верхние полурешётки, а также множество простых идеалов с введенной на нём топологией.
Глава 1.
1. Упорядоченные множества.
Определение
:
Упорядоченным множеством
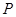 называется непустое множество, на котором определено бинарное отношение называется непустое множество, на котором определено бинарное отношение 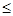 , удовлетворяющее для всех , удовлетворяющее для всех 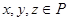 следующим условиям: следующим условиям:
Реклама

1.Рефлексивность: 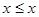 . .
2.Антисимметричность: если 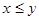 и и 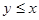 , то , то 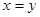 . .
3.Транзитивность: если 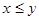 и и 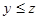 , то , то 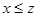 . .
Если 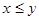 и и 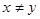 , то говорят, что , то говорят, что 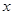 меньше меньше 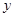 или или 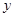 больше больше 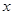 , и пишут , и пишут 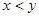 или или 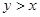 . .
Примеры упорядоченных множеств:
1. Множество целых положительных чисел, а 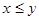 означает, что означает, что 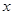 делит делит 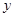 . .
2. Множество всех действительных функций  на отрезке на отрезке 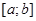 и и
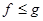 означает, что означает, что 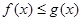 для для 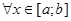 . .
Определение:
Цепью
называется упорядоченное множество, на котором для 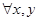 имеет место имеет место 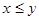 или или 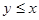 . .
Используя отношение порядка, можно получить графическое представление любого конечного упорядоченного множества 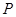 . Изобразим каждый элемент множества . Изобразим каждый элемент множества 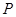 в виде небольшого кружка, располагая в виде небольшого кружка, располагая 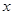 выше выше 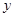 , если , если 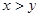 . Соединим . Соединим 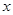 и и 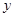 отрезком. Полученная фигура называется диаграммой
упорядоченного множества отрезком. Полученная фигура называется диаграммой
упорядоченного множества 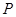 . .
Примеры диаграмм упорядоченных множеств:
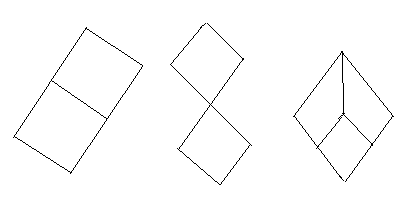
2. Решётки
Определение:
Верхней гранью
подмножества 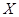 в упорядоченном множестве в упорядоченном множестве 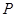 называется элемент называется элемент 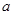 из из 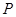 , больший или равный всех , больший или равный всех 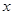 из из 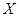 . .
Определение:
Точная верхняя грань
подмножества 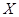 упорядоченного множества упорядоченного множества 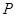 – это такая его верхняя грань, которая меньше любой другой его верхней грани. Обозначается символом – это такая его верхняя грань, которая меньше любой другой его верхней грани. Обозначается символом 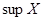 и читается «супремум X». и читается «супремум X».
Согласно аксиоме антисимметричности упорядоченного множества, если точная верхняя грань существует, то она единственна.
Понятия нижней грани и точной нижней грани (которая обозначается 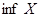 и читается «инфинум») определяются двойственно. Также, согласно аксиоме антисимметричности упорядоченного множества, если точная нижняя грань и читается «инфинум») определяются двойственно. Также, согласно аксиоме антисимметричности упорядоченного множества, если точная нижняя грань 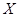 существует, то она единственна. существует, то она единственна.
Определение:
Решёткой
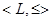 называется упорядоченное множество называется упорядоченное множество 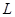 , в котором любые два элемента , в котором любые два элемента 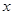 и и 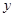 имеют точную нижнюю грань, обозначаемую имеют точную нижнюю грань, обозначаемую 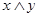 , и точную верхнюю грань, обозначаемую , и точную верхнюю грань, обозначаемую 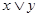 . .
Примеры решёток:
1. Любая цепь является решёткой, т.к. 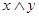 совпадает с меньшим, а совпадает с меньшим, а 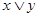 с большим из элементов с большим из элементов 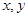 . .
2.
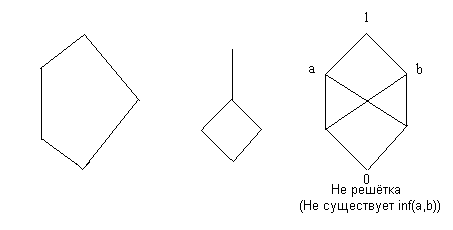
Наибольший элемент, то есть элемент, больший или равный каждого элемента упорядоченного множества, обозначают 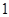 , а наименьший элемент, то есть меньший или равный каждого элемента упорядоченного множества, обозначают , а наименьший элемент, то есть меньший или равный каждого элемента упорядоченного множества, обозначают  . .
На решётке можно рассматривать две бинарные операции:
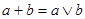 - сложение и - сложение и
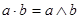 - произведение - произведение
Эти операции обладают следующими свойствами:
1. 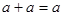 , , 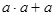 идемпотентность идемпотентность
2. 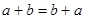 , , 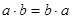 коммутативность коммутативность
3. 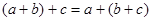 , ,
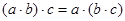 ассоциативность ассоциативность
4. 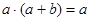 , ,
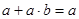 законы поглощения законы поглощения
Теорема
. Пусть
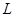 - множество с двумя бинарными операциями
- множество с двумя бинарными операциями 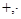 , обладающими свойствами (1) – (4). Тогда отношение , обладающими свойствами (1) – (4). Тогда отношение 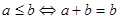 (или (или 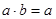 ) является порядком на ) является порядком на
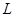 , а возникающее упорядоченное множество оказывается решёткой, причём:
, а возникающее упорядоченное множество оказывается решёткой, причём:
Реклама

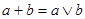
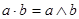
Доказательство.
Рефлексивность отношения 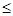 вытекает из свойства (1). Заметим, что оно является следствием свойства (4): вытекает из свойства (1). Заметим, что оно является следствием свойства (4):
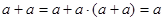
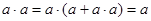
Если 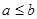 и и 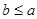 , то есть , то есть 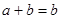 и и 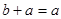 , то в силу свойства (2), получим , то в силу свойства (2), получим 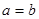 . Это означает, что отношение . Это означает, что отношение 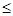 антисимметрично. антисимметрично.
Если 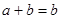 и и 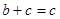 , то применяя свойство (3), получим: , то применяя свойство (3), получим: 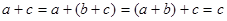 , что доказывает транзитивность отношения , что доказывает транзитивность отношения 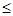 . .
Применяя свойства (3), (1), (2), получим:
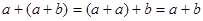 , ,
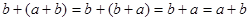 . .
Следовательно, 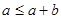 и и 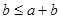
Если 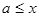 и и 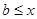 , то используя свойства (1) – (3), имеем: , то используя свойства (1) – (3), имеем:
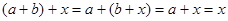 , т.е. , т.е. 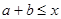
По определению точней верхней грани убедимся, что
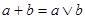
Из свойств (2), (4) вытекает, что 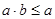 и и 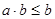
Если 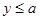 и и 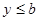 , то по свойствам (3), (4) получим: , то по свойствам (3), (4) получим:
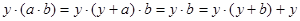
Отсюда по свойствам (2) и (4) следует, что
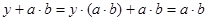 , т.е. , т.е.
Таким образом, 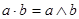 . ■ . ■
Пусть 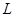 решётка, тогда её наибольший элемент решётка, тогда её наибольший элемент 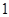 характеризуется одним из свойств: характеризуется одним из свойств:
1.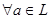 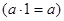
2.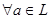 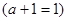 . .
Аналогично характеризуется наименьший элемент 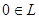 : :
1.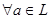 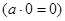
2.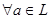 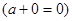 . .
3. Дистрибутивные решётки.
Определение:
Решётка 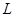 называется дистрибутивной
, если для называется дистрибутивной
, если для 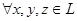 выполняется: выполняется:
1. 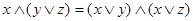
2. 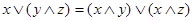
В любой решётке тождества (1) и (2) равносильны. Доказательство этого факта содержится в книге [1], стр. 24.
Теорема:
Решётка 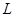 с 0 и 1 является дистрибутивной тогда и только тогда, когда она не содержит подрешёток вида с 0 и 1 является дистрибутивной тогда и только тогда, когда она не содержит подрешёток вида
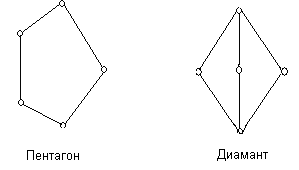
Доказательство этого факта можно найти в книге [2].
Далее под словом “решётка” понимается произвольная дистрибутивная решётка с 0 и 1 (причём 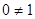 ). ).
Определение:
Непустое множество 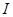 называется идеалом
в решётке называется идеалом
в решётке 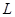 , если выполняются условия: , если выполняются условия:
1. 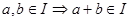
2. 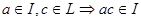
Определение:
Идеал 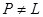 в решётке в решётке 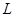 называется простым
, если называется простым
, если
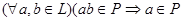 или или 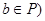 . .
Идеал, порождённый множеством Н
(т.е. наименьший идеал, содержащий H
), будет обозначаться (Н].
Если Н = {
a
}
, то вместо ({
a
}]
будем писать (
a
]
и называть (
a
] главным идеалом.
Обозначим через I
(
L
)
множество всех идеалов решётки L. I
(
L
)
будем называть решёткой идеалов.
Определение:
Решётки 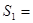 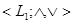 и и 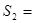 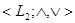 называются изоморфными
(обозначение: называются изоморфными
(обозначение: 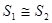 ), если существует взаимно однозначное отображение ), если существует взаимно однозначное отображение 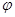 , называемое изоморфизмом,
множества , называемое изоморфизмом,
множества 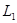 на множество на множество 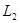 , такое, что , такое, что
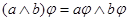 , ,
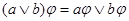 . .
4. Топологические пространства.
Определение:
Топологическое пространство
– это непустое множество 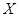 с некоторой системой с некоторой системой 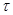 выделенных его подмножеств, которая удовлетворяет аксиомам: выделенных его подмножеств, которая удовлетворяет аксиомам:
1. Пустое множество и само пространство 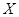 принадлежит системе принадлежит системе 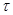 : : 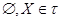 . .
2. Пересечение любого конечного числа множеств из 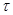 принадлежит принадлежит 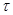 , т.е. , т.е. 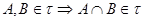 . .
3. Объединение любого семейства множеств из 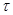 принадлежит принадлежит 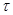 , т.е. , т.е. 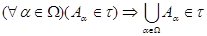 . .
Таким образом, топологическое пространство – это пара <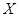 , , 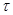 >, где >, где 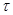 - такое множество подмножеств в - такое множество подмножеств в 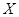 , что , что 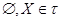 и и 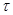 замкнуто относительно конечных пересечений и произвольных объединений. Множества из замкнуто относительно конечных пересечений и произвольных объединений. Множества из 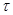 называют открытыми, а их дополнения в называют открытыми, а их дополнения в 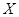 замкнутыми. замкнутыми.
Определение:
Пространство называется компактным
, если в любом его открытом покрытии можно выбрать конечное подпокрытие.
Определение:
Подмножество пространства называется компактным
, если в любом его открытом покрытии можно выбрать конечное подпокрытие.
Определение:
Топологическое пространство называется 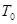 - пространством
, если для любых двух различных его точек существует открытое множество, содержащее ровно одну из этих точек. - пространством
, если для любых двух различных его точек существует открытое множество, содержащее ровно одну из этих точек.
Глава 2.
1. Верхние полурешётки.
Определение:
Ч.у. множество называется верхней полурешёткой
, если sup
{
a
,
b
}
существует для любых элементов a
и b
.
Определение:
Непустое множество I
верхней полурешётки L
называется идеалом
, если для любых 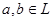 включение включение 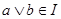 имеет место тогда и только тогда, когда имеет место тогда и только тогда, когда 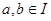 . .
Определение
: Верхняя полурешётка 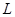 называется дистрибутивной
, если неравенство называется дистрибутивной
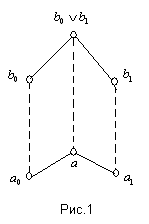
, если неравенство 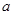 ≤ ≤ 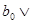 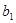 ( (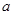 , , 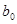 , , 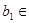 L) влечёт за собой существование элементов L) влечёт за собой существование элементов 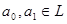 , таких, что , таких, что 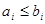 , , 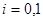 , и , и 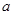 = = 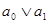 .(рис.1). Заметим, что элементы .(рис.1). Заметим, что элементы 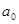 и и 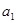 не обязательно единственны. не обязательно единственны.
Некоторые простейшие свойства дистрибутивной верхней полурешётки даёт:
Лемма 1
:
(*). Если <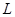 , ,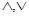 > - произвольная полурешётка, то верхняя полурешётка > - произвольная полурешётка, то верхняя полурешётка 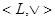 дистрибутивна тогда и только тогда, когда решётка дистрибутивна тогда и только тогда, когда решётка 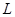 дистрибутивна. дистрибутивна.
(**). Если верхняя полурешётка 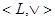 дистрибутивна, то для любых дистрибутивна, то для любых 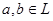 существует элемент существует элемент 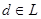 , такой, что , такой, что 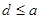 и и 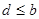 . Следовательно, множество . Следовательно, множество 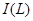 является решёткой. является решёткой.
(***). Верхняя полурешётка 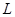 дистрибутивна тогда и только тогда, когда множество дистрибутивна тогда и только тогда, когда множество 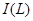 является дистрибутивной решёткой. является дистрибутивной решёткой.
Доказательство.
(*). 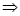 < <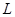 , ,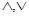 > - дистрибутивна и > - дистрибутивна и 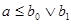 , то для элементов , то для элементов 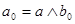 , , 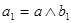 , справедливо равенство , справедливо равенство 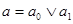 : :
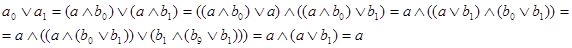
значит, полурешётка <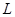 , ,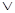 > - дистрибутивна. > - дистрибутивна.
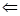  < <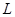 , ,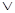 > - дистрибутивна. Пусть решётка > - дистрибутивна. Пусть решётка 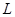 содержит диамант или пентагон (рис.2). содержит диамант или пентагон (рис.2).
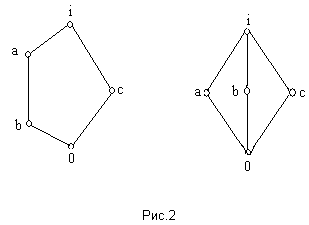
1) Пусть решётка 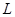 содержит пентагон, содержит пентагон, 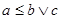 . Нужно найти такие элементы . Нужно найти такие элементы 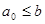 и и 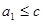 , чтобы выполнялось равенство , чтобы выполнялось равенство 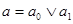 . Но множество элементов меньших b
или c
состоит из элементов {0,
b
,
c
}
и их нижняя граница не даст a
.
Получили противоречие с тем, что < . Но множество элементов меньших b
или c
состоит из элементов {0,
b
,
c
}
и их нижняя граница не даст a
.
Получили противоречие с тем, что <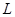 , ,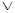 > - дистрибутивна. Значит, наше предположение неверно и решётка > - дистрибутивна. Значит, наше предположение неверно и решётка 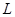 не содержит пентагона. не содержит пентагона.
2) Пусть решётка 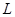 содержит диамант, содержит диамант, 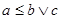 . Аналогично, множество элементов меньших b
или c
состоит из элементов {0,
b
,
c
},
их нижняя граница не даст a
.
Значит, решётка . Аналогично, множество элементов меньших b
или c
состоит из элементов {0,
b
,
c
},
их нижняя граница не даст a
.
Значит, решётка 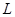 не содержит диаманта. не содержит диаманта.
Можно сделать вывод, что решётка 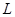 дистрибутивна. дистрибутивна.
(**). Имеем 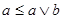 , поэтому , поэтому 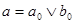 , где , где 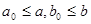 (по определению дистрибутивной полурешётки). Кроме того, (по определению дистрибутивной полурешётки). Кроме того, 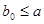 является нижней границей элементов является нижней границей элементов 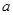 и и 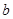 . .
Рассмотрим идеалы, содержащие элемент 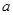 и и 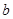 - - 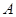 и и 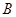 . Тогда . Тогда 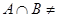 Ø ,т.к. Ø ,т.к. 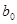 , нижняя граница элементов a
и b
, содержится там. , нижняя граница элементов a
и b
, содержится там.
Покажем, что I
(
L
)
– решётка, т.е. существуют точные нижняя и верхняя грани для любых A
и B
.
Покажем, что 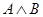 совпадает с пересечением идеалов A
и B
.
Во-первых,
совпадает с пересечением идеалов A
и B
.
Во-первых, 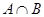 - идеал. Действительно, - идеал. Действительно, 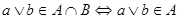 и и 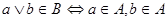 и и 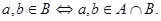 Во-вторых, пусть идеал Во-вторых, пусть идеал 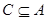 и и 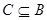 . Тогда . Тогда 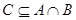 , т.е. , т.е. 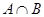 - точная нижняя грань идеалов A
и B
,
т.е. - точная нижняя грань идеалов A
и B
,
т.е. 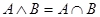 . .
Теперь покажем, что 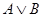 совпадает с пересечением всех идеалов совпадает с пересечением всех идеалов 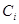 , содержащих A
и B
.
Обозначим , содержащих A
и B
.
Обозначим 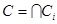 . Поскольку . Поскольку 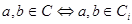 для для 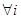 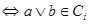 для
для 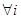 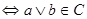 ,
то C
идеал. По определению C
он будет наименьшим идеалом, содержащим A
и B
. ,
то C
идеал. По определению C
он будет наименьшим идеалом, содержащим A
и B
.
(***). 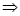 Пусть Пусть 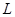 – верхняя дистрибутивная полурешётка. Покажем, что – верхняя дистрибутивная полурешётка. Покажем, что
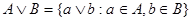 . .
Пусть 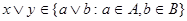 , т.е. , т.е. 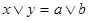 (рис.3), для некоторых (рис.3), для некоторых 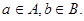
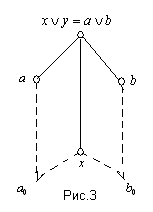
Понятно, что 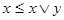 . По дистрибутивности, существуют . По дистрибутивности, существуют 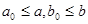 такие, что такие, что 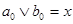 . Т.к. A
– идеал, то . Т.к. A
– идеал, то 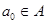 , потому что , потому что 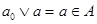 . Аналогично, . Аналогично, 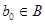 . Т.е. . Т.е. 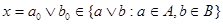 . Точно также, . Точно также, 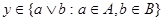 . Если . Если 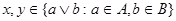 , то легко показать, что , то легко показать, что 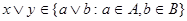 . .
Доказали, что 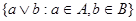 - идеал. Очевидно, он является верхней гранью идеалов A
и B
.
Если C
содержит A
и B
, то C
будет содержать элементы - идеал. Очевидно, он является верхней гранью идеалов A
и B
.
Если C
содержит A
и B
, то C
будет содержать элементы 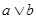 для любых для любых 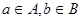 , т.е. , т.е. 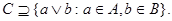 Поэтому Поэтому 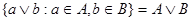 , поскольку , поскольку 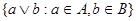 является верхней гранью идеалов A
и B
и содержится в любой верхней грани. является верхней гранью идеалов A
и B
и содержится в любой верхней грани.
Теперь покажем, что выполняется равенство:
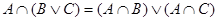 . .
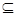 . Пусть . Пусть 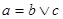 , где , где 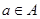 , ,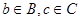 . Т.к. . Т.к. 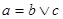 , то , то  , откуда , откуда 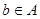 и следовательно и следовательно 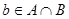 . Аналогично, . Аналогично, 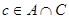 , значит, , значит, 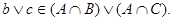
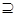 . Пусть . Пусть 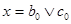 ,где ,где 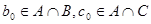 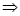 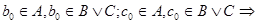 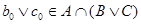 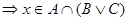 . .
Отсюда следует дистрибутивность решётки 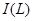 . .
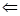 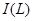 – дистрибутивная решётка, – дистрибутивная решётка, 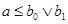 . Теперь рассмотрим идеалы, образованные этими элементами: . Теперь рассмотрим идеалы, образованные этими элементами:
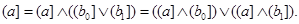
(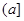 ,будет нижней границей для ,будет нижней границей для 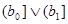 ). Поэтому ). Поэтому 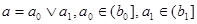 , что и доказывает дистрибутивность полурешётки , что и доказывает дистрибутивность полурешётки 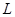 . ■ . ■
2. Стоуново пространство.
Определение
: Подмножество 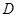 верхней полурешётки верхней полурешётки 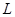 называется коидеалом
, если называется коидеалом
, если 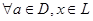 из неравенства из неравенства 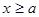 следует следует 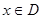 и и 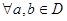 существует нижняя граница существует нижняя граница 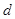 множества множества 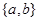 , такая, что , такая, что 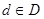 . .
Определение:
Идеал 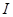 полурешётки полурешётки 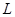 называется простым
, если называется простым
, если 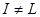 и множество и множество 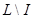 является коидеалом. является коидеалом.
В дальнейшем нам потребуется лемма Цорна, являющаяся эквивалентным утверждением аксиоме выбора.
Лемма Цорна.
Пусть
A
– множество и
X
– непустое подмножество множества
P
(
A
). Предположим, что
X
обладает следующим свойством: если
C
– цепь в <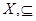 >, то >, то 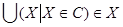 . Тогда
X
обладает максимальным элементом. . Тогда
X
обладает максимальным элементом.
Лемма 2
: Пусть 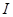 – произвольный идеал и – произвольный идеал и 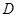 – непустой коидеал дистрибутивной верхней полурешётки – непустой коидеал дистрибутивной верхней полурешётки 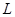 . Если . Если 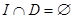 , то в полурешётке , то в полурешётке 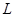 существует простой идеал существует простой идеал 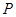 такой, что такой, что 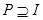 и и 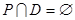 . .
Доказательство.
Пусть X
– множество всех идеалов в L
,
содержащих I
и не пересекающихся с D
. Покажем, что X
удовлетворяет лемме Цорна.
Пусть C
–
произвольная цепь в X
и 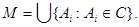 Если Если 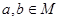 , то , то 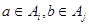 для некоторых для некоторых 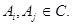 Пусть для определённости Пусть для определённости 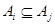 . Тогда . Тогда 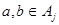 и и 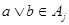 , т.к. , т.к. 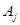 - идеал. Поэтому - идеал. Поэтому 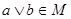 . Обратно, пусть . Обратно, пусть 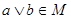 , тогда , тогда 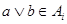 , для некоторого , для некоторого 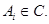 Получаем Получаем 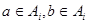 , откуда , откуда 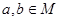 . .
Доказали, что M –
идеал, очевидно, содержащий I
и не пересекающийся с D
, т.е. 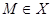 . По лемме Цорна X
обладает максимальным элементом, т.е. максимальным идеалом P
среди содержащих I
и не пересекающихся с D
. . По лемме Цорна X
обладает максимальным элементом, т.е. максимальным идеалом P
среди содержащих I
и не пересекающихся с D
.
Покажем, что P
– простой. Для этого достаточно доказать, что L
\
P
является коидеалом. Пусть 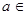 L
\
P
и L
\
P
и 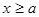 . Поскольку . Поскольку 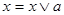 , то , то 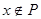 , иначе в противном случае , иначе в противном случае 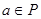 по определению идеала. Следовательно, по определению идеала. Следовательно, 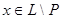 . Если . Если 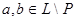 , то , то 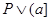 и и 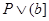 пересекающихся с D
в силу максимальности P
.
Получаем пересекающихся с D
в силу максимальности P
.
Получаем 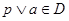 и и 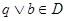 для некоторых элементов для некоторых элементов 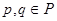 . Существует элемент . Существует элемент 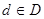 такой, что такой, что 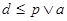 и и 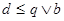 , по определению коидеала, следовательно , по определению коидеала, следовательно 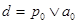 и и 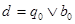 для некоторых для некоторых 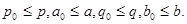 Заметим, что Заметим, что 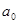 и и 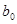 не лежат в P
,
т.к. в противном случае не лежат в P
,
т.к. в противном случае 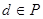 . .
Далее, 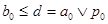 , поэтому , поэтому 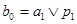 для некоторых для некоторых 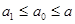 и и  . Как и прежде . Как и прежде 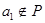 . Кроме того . Кроме того 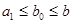 , поэтому , поэтому 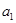 - нижняя грань элементов a
и b
,
не лежащая в P
. ■ - нижняя грань элементов a
и b
,
не лежащая в P
. ■
В дальнейшем, через 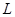 будем обозначать дистрибутивную верхнюю полурешётку с нулём, через будем обозначать дистрибутивную верхнюю полурешётку с нулём, через 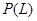 множество всех простых идеалов полурешётки множество всех простых идеалов полурешётки 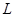 . .
Множества вида 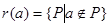 представляют элементы полурешётки представляют элементы полурешётки 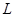 в ч.у. множестве в ч.у. множестве 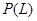 (т.е. (т.е. 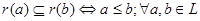 ). Сделаем все такие множества открытыми в некоторой топологии. ). Сделаем все такие множества открытыми в некоторой топологии.
Обозначим через 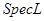 топологическое пространство, определённое на множестве топологическое пространство, определённое на множестве 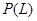 . Пространство SpecL
будем называть стоуновым пространством
полурешётки L
. . Пространство SpecL
будем называть стоуновым пространством
полурешётки L
.
Лемма 3
: Для любого идеала
I
полурешётки
L
положим:
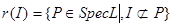
Тогда множества вида 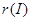 исчерпывают все открытые множества в стоуновом пространстве
SpecL
. исчерпывают все открытые множества в стоуновом пространстве
SpecL
.
Доказательство.
Нужно проверить выполнение аксиом топологического пространства.
1) Рассмотрим идеал, образованный 0. Тогда
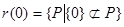 , ,
но 0 лежит в любом идеале, а значит 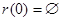 . .
2) Возьмём произвольные идеалы 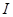 и и 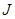 полурешётки полурешётки 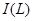 и рассмотрим и рассмотрим
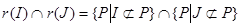 
Пусть 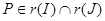 . Тогда существуют элементы a . Тогда существуют элементы a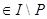 и
и 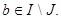 Отсюда следует, что Отсюда следует, что 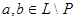 , где L
\
P
– коидеал. По определению коидеала существует элемент d , где L
\
P
– коидеал. По определению коидеала существует элемент d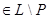 такой, что
такой, что 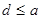 и и 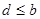 , значит, , значит,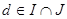 . Т.к. . Т.к. 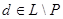 , следовательно, , следовательно, 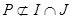 . Получаем, что . Получаем, что 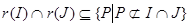 . .
Обратное включение очевидно.
2) Пусть 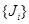 - произвольное семейство идеалов. Через - произвольное семейство идеалов. Через 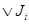 обозначим множество всех точных верхних граней конечного числа элементов, являющихся представителями семейства обозначим множество всех точных верхних граней конечного числа элементов, являющихся представителями семейства 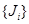 . Покажем, что . Покажем, что 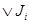 - идеал. Пусть - идеал. Пусть 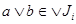 , тогда , тогда 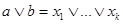 , где , где 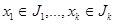 для некоторого идеала для некоторого идеала 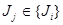 . Тогда . Тогда 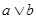 лежит в идеале лежит в идеале 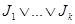 , следовательно, , следовательно, 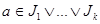 и и 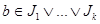 , т.е. , т.е. 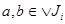 . Обратно очевидно. . Обратно очевидно.
Доказали, что 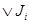 - идеал. Теперь рассмотрим произвольное объединение. - идеал. Теперь рассмотрим произвольное объединение.
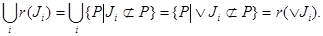 ■ ■
Лемма 4
: Подмножества вида 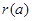 пространства пространства 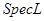 можно охарактеризовать как компактные открытые множества. можно охарактеризовать как компактные открытые множества.
Доказательство.
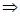 Действительно, если семейство Действительно, если семейство 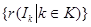 открытых множеств покрывает множество открытых множеств покрывает множество 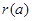 , т.е. , т.е. 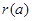 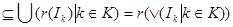 , то , то 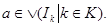 Отсюда следует, что Отсюда следует, что 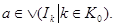 для некоторого конечного подмножества для некоторого конечного подмножества 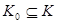 , поэтому , поэтому 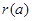 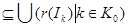 . Таким образом, множество . Таким образом, множество 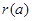 компактно. компактно.
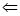 Пусть открытое множество r
(
I
)
компактно, тогда Пусть открытое множество r
(
I
)
компактно, тогда 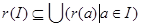 и можно выделить конечное подпокрытие и можно выделить конечное подпокрытие 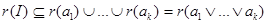 для некоторых для некоторых 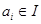 . .
Покажем, что I
порождается элементом 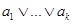 . .
Предположим, что это не так, и в идеале I
найдётся элемент b
не лежащий в 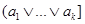 . Тогда [
b
)
– коидеал, не пересекающийся с . Тогда [
b
)
– коидеал, не пересекающийся с 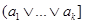 . По лемме 2 найдётся простой идеал P
содержащий . По лемме 2 найдётся простой идеал P
содержащий 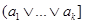 и не пересекающийся с [
b
).
Получаем, и не пересекающийся с [
b
).
Получаем, 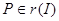 , т.к. , т.к. 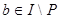 (т.е. (т.е. 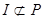 ), но ), но 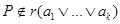 , т.к. , т.к. 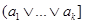 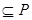 , противоречие. Следовательно, компактным открытым множеством r
(
I
)
будет только в случае, если , противоречие. Следовательно, компактным открытым множеством r
(
I
)
будет только в случае, если 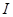 - главный идеал.■ - главный идеал.■
Предложение 5:
Пространство 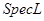 является является 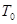 - пространством. - пространством.
Доказательство.
Рассмотрим два различных простых идеала 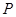 и Q
. Хотя бы один не содержится в другом. Допустим для определённости, что и Q
. Хотя бы один не содержится в другом. Допустим для определённости, что 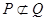 . Тогда r
(
P
)
содержит Q
, но не содержит P
,
т.е. SpecL
является . Тогда r
(
P
)
содержит Q
, но не содержит P
,
т.е. SpecL
является 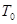 - пространством. ■ - пространством. ■
Теорема 6
: Стоуново пространство 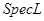 определяет полурешётку определяет полурешётку 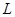 с точностью до изоморфизма. с точностью до изоморфизма.
Доказательство.
Нужно показать, что две полурешётки 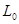 и и 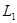 изоморфны тогда и только тогда, когда пространства изоморфны тогда и только тогда, когда пространства 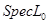 и и  гомеоморфны. гомеоморфны.
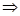 Очевидно, если решётки изоморфны, то пространства, образованные этими полурешётками будут совпадать. Очевидно, если решётки изоморфны, то пространства, образованные этими полурешётками будут совпадать.
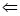 Пусть Пусть 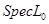 и и 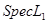 гомеоморфны ( гомеоморфны (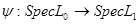 ) и ) и 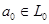 . Тогда a
определяет компактное открытое множество r
(
a
) . Тогда a
определяет компактное открытое множество r
(
a
)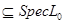 .
Множеству r
(
a
)
соответствует компактное открытое множество .
Множеству r
(
a
)
соответствует компактное открытое множество 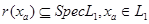 , с однозначно определённым элементом , с однозначно определённым элементом 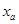 по лемме 4. Таким образом получаем отображение по лемме 4. Таким образом получаем отображение 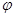 : : 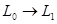 , при котором , при котором 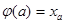 . Покажем, что . Покажем, что 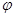 - изоморфизм решёток. Если a
,
b
–
различные элементы из - изоморфизм решёток. Если a
,
b
–
различные элементы из 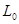 , то , то 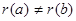 , следовательно, , следовательно, 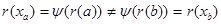 , поэтому , поэтому 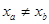 и и 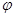 - инъекция. - инъекция.
Для произвольного 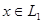 открытому множеству открытому множеству 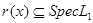 соответствует соответствует 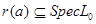 и очевидно и очевидно 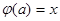 , что показывает сюръективность , что показывает сюръективность 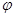 . .
Пусть a
,
b
–
произвольные элементы из 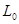 . Заметим, что . Заметим, что 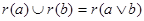 . Открытому множеству . Открытому множеству 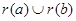 при гомеоморфизме при гомеоморфизме 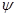 соответствует открытое множество соответствует открытое множество 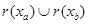 , а , а 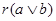 соответствует соответствует 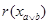 . Следовательно, . Следовательно, 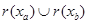 = =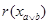 . Поскольку . Поскольку 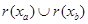 = = , то , то 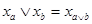 , т.е. , т.е. 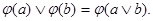 ■ ■
Литература.
1. Биргкоф Г. Теория решёток. – М.:Наука, 1984.
2. Гретцер Г. Общая теория решёток. – М.: Мир, 1982.
3. Чермных В.В. Полукольца. – Киров.: ВГПУ, 1997.
|