Содержание.
Содержание......................................................................................................................................................... 2
1. Оптимальное производственное планирование........................................................ 3
1.1 Линейная задача производственного планирования............................................................. 3
1.2 Двойственная задача линейного программирования............................................................. 4
1.3 Задача о комплектном плане.............................................................................................................. 5
1.4 Оптимальное распределение инвестиций..................................................................................... 6
2. Анализ финансовых операций и инструментов.......................................................... 9
2.1 Принятие решений в условиях неопределенности.................................................................... 9
2.2 Анализ доходности и рискованности финансовых операций......................................... 11
2.3 Статистический анализ денежных потоков............................................................................. 13
2.4 Задача формирования оптимального портфеля ценных бумаг....................................... 17
3. Модели сотрудничества и конкуренции.......................................................................... 19
3.1 Сотрудничество и конкуренция двух фирм на рынке одного товара............................ 19
3.2 Кооперативная биматричная игра как модель сотрудничества и конкуренции двух участников.................................................................................................................................................................................. 20
3.3 Матричная игра как модель конкуренции и сотрудничества............................................ 22
4. Социально-экономическая структура общества.................................................... 24
4.1 Модель распределения богатства в обществе........................................................................... 24
Реклама

4.2 Распределение общества по получаемому доходу............................................................... 26
1. Оптимальное производственное планирование.
48 30 29 10 - удельные прибыли
нормы расхода - 3 2 4 3 198
2 3 1 2 96 - запасы ресурсов
6 5 1 0 228
Обозначим x1,x2,x3,x4 - число единиц 1-й,2-й,3-й,4-й продукции, которые планируем произвести. При этом можно использовать только имеющиеся запасы ресурсов. Целью является получение максимальной прибыли. Получаем следующую математическую модель оптимального планирования:
P(x1,x2,x3,x4) =48*x1+30*x2+29*x3+10*x4 --> max
3*x1+ 2*x2+ 4*x3+ 3*x4<=198
2*x1+ 3*x2+ 1*x3+ 2*x4<= 96
6*x1+ 5*x2+ 1*x3+ 0*x4<=228
x1,x2,x3,x4>=0
Для решения полученной задачи в каждое неравенство добавим неотрицательную переменную. После этого неравенства превратятся в равенства, в силу этого добавляемые переменные называются балансовыми. Получается задача ЛП на максимум, все переменные неотрицательны, все ограничения есть равенства, и есть базисный набор переменных: x5 - в 1-м равенстве, x6 - во 2-м и x7 - в 3-м.
P(x1,x2,x3,x4)=48*x1+30*x2+29*x3+10*x4+ 0*x5+ 0*x6+ 0*x7 -->max
3*x1+ 2*x2+ 4*x3+ 3*x4+ x5 =198
2*x1+ 3*x2+ 1*x3+ 2*x4 + x6 = 96
6*x1+ 5*x2+ 1*x3+ 0*x4 + x7=228
x1,x2,x3,x4,x5,x6,x7>=0
| 48 |
30 |
29 |
10 |
0 |
0 |
0 |
Hi
/qis |
| С |
Б |
Н |
Х1 |
Х2 |
Х3 |
Х4 |
Х5 |
Х6 |
Х7 |
| 0 |
Х5 |
198 |
3 |
2 |
4 |
3 |
1 |
0 |
0 |
66 |
| 0 |
Х6 |
96 |
2 |
3 |
1 |
2 |
0 |
1 |
0 |
48 |
| 0 |
Х7 |
228 |
6 |
5 |
1 |
0 |
0 |
0 |
1 |
38 |
| Р |
0 |
-48 |
-30 |
-29 |
-10 |
0 |
0 |
0 |
| 0 |
Х5 |
84 |
0 |
-0.5 |
3.5 |
3 |
1 |
0 |
-0.5 |
24 |
| 0 |
Х6 |
20 |
0 |
1.33 |
0.67 |
2 |
0 |
1 |
-0.33 |
30 |
| 48 |
Х1 |
38 |
1 |
0.83 |
0.17 |
0 |
0 |
0 |
0.17 |
228 |
| Р |
1824 |
0 |
10 |
-21 |
-10 |
0 |
0 |
8 |
| 29 |
Х3 |
24 |
0 |
-0.14 |
1 |
0.86 |
0.29 |
0 |
-0.14 |
| 0 |
Х6 |
20 |
0 |
1.43 |
0 |
1.43 |
-0.19 |
1 |
-0.24 |
| 48 |
Х1 |
34 |
1 |
0.86 |
0 |
-0.14 |
-0.05 |
0 |
0.19 |
| Р |
2328 |
0 |
7 |
0 |
8 |
6 |
0 |
5 |
Так как все оценочные коэффициенты неотрицательны, то получено оптимальное решение. Оптимальное решение: x1=34, x2=0, x3=24, x4=0, x5=0, x6=20, x7=0. Максимум целевой функции Pmax
= 2328.
Ресурсы 1 и 3 являются «узким местом» производства, так как при выполнении оптимального плана они используются полностью (без остатка).
исходная задача двойственная задача
CX-->max YB-->min
AX<=B, X>=0 YA>=C, Y>=0
P= 48*x1+30*x2+29*x3+10*x4 -->max S= 198*y1+96*y2+228*y3 -->min
3*x1+2*x2+4*x3+3*x4<=198 3*y1+2*y2+6*y3>=48
2*x1+3*x2+1*x3+2*x4<=96 2*y1+3*y2+5*y3>=30
6*x1+5*x2+1*x3+0*x4<=228 4*y1+1*y2+1*y3>=29
x1,x2,x3,x4>=0 3*y1+2*y2+0*y3>=10
y1,y2,y3>=0
Первый способ:
По первой теореме двойственности, оптимальные решения двойственной задачи (y1,y2,y3) равны оценочным коэффициентам при балансовых переменных последней симплекс-таблицы: у1=6, у2=0, у3=5. А экстремум двойственной задачи Smin
=2328.
Второй способ:
По второй теореме двойственности, если какая-то компонента оптимального решения исходной задачи отлична от нуля, то соответствующее ей ограничение двойственной задачи на ее оптимальном решении выполняется как строгое равенство. А если какое-то из ограничений исходной задачи на ее оптимальном решении выполняется как строгое неравенство, то соответствующая компонента оптимального решения двойственной задачи обязательно равна нулю.
Реклама

Так как балансовая переменная второго ограничения (х6) отлична от нуля, следовательно оно выполняется на оптимальном решении как строгое неравенство, а поэтому у2=0. Так как х1 и х3 отличны от нуля, то получаем следующую систему уравнений: 3*у1 +6*у3 = 48
4*у1 + у3 = 29
Решая их, получаем оптимальные решения двойственной задачи: у1=6, у2=0, у3=5.
Имеем соотношения: x3:x1= 1; x4:x2=3 или х3=х1; х4=3*х2. Подставив эти выражения, получим задачу ЛП с двумя переменными.
77*х1 +60*х2 -max
7*х1 +11*х2 ≤ 198
3*х1 + 9*х2 ≤ 96
7*х1 +5*х2 ≤ 228
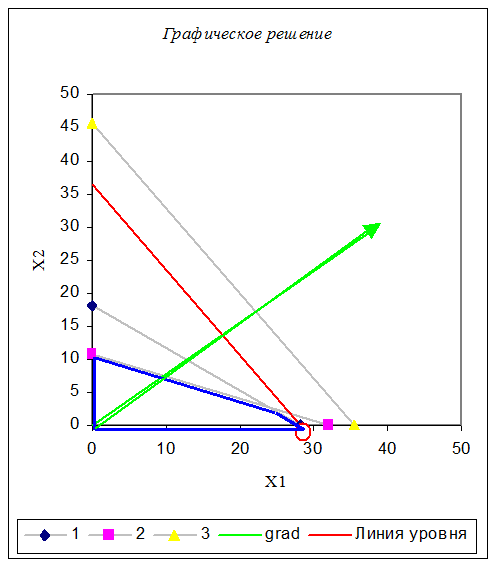
 Наносим эти ограничения на плоскость х1х2 и ищем на допустимом множестве максимум функции. Для этого строим градиент grad(77,60). Искомая точка с координатами х1=0; х2»28.29 и максимум прибыли max»2178. Наносим эти ограничения на плоскость х1х2 и ищем на допустимом множестве максимум функции. Для этого строим градиент grad(77,60). Искомая точка с координатами х1=0; х2»28.29 и максимум прибыли max»2178.
Имеем: 4 фирмы, инвестиции в размере 700 тыс. рублей. По этим 4 фирмам их нужно распределить. Размер инвестиций кратен 100 тыс. рублей. Эффект от направления i-й фирме инвестиций в размере m (сотен тыс. рублей) выражается функцией fi(m). Приходим к задаче:
f1(x1)+f2(x2)+f3(x3)+f4(x4)-->max
x1+x2+x3+x4<=7
x1,x2,x3,x4>=0
где xi - неизвестный размер инвестиций i-й фирме. Эта задача решается методом динамического программирования: последовательно ищется оптимальное распределение для k=2,3 и 4 фирм. Пусть первым двум фирмам выделено m инвестиций, обозначим z2(m) величину инвестиций 2-й фирме, при которой сумма f2(z2(j))+f1(m-z2(j)), 0<=j<=m максимальна, саму эту максимальную величину обозначим F2(m). Далее действуем также: находим функции z3 и F3 и т.д. На k-ом шаге для нахождения Fk(m) используем основное рекуррентное соотношение:
Fk(m)=max{fk(j)+F{k-1}(m-j): 0<=j<=7}
Исходные данные:
Таблица №1.
| x |
0 |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
| f1
(x1
) |
0 |
28 |
45 |
65 |
78 |
90 |
102 |
113 |
| f2
(x2
) |
0 |
25 |
41 |
55 |
65 |
75 |
80 |
85 |
| f3
(x3
) |
0 |
15 |
25 |
40 |
50 |
62 |
73 |
82 |
| f4
(x4
) |
0 |
33 |
33 |
42 |
48 |
53 |
56 |
58 |
Заполняем следующую таблицу. Значения f2
(x2
) складываем со значениями F1
(m-x2
) = f2
(m-x2
) и на каждой северо-восточной диагонали находим наибольшее число, которое отмечаем и указываем соответствующее значение z2
.
Таблица №2.
| m-x2
|
0 |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
| x2
|
f2
(x2
)/ F1
(m-x2
) |
0 |
28 |
45 |
65 |
78 |
90 |
102 |
113 |
| 0 |
0 |
0 |
28 |
45 |
65 |
78 |
90 |
102 |
113 |
| 100 |
25 |
25 |
53 |
70 |
90 |
103 |
115 |
127 |
| 200 |
41 |
41 |
69 |
86 |
106 |
119 |
131 |
| 300 |
55 |
55 |
83 |
100 |
120 |
133 |
| 400 |
65 |
65 |
93 |
110 |
130 |
| 500 |
75 |
75 |
103 |
120 |
| 600 |
80 |
80 |
108 |
| 700 |
85 |
85 |
Голубым цветом обозначен максимальный суммарный эффект от выделения соответствующего размера инвестиций 2-м предприятиям.
Таблица №3.
| m |
0 |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
| F2
(m) |
0 |
28 |
53 |
70 |
90 |
106 |
120 |
133 |
| z2
(m) |
0 |
0 |
100 |
100 |
100 |
200 |
300 |
300 |
Продолжая процесс, табулируем функции F3
(m) и z3
(m).
Таблица №4.
| m-x3
|
0 |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
| x3
|
f3
(x3
)/ F2
(m-x3
) |
0 |
28 |
53 |
70 |
90 |
106 |
120 |
133 |
| 0 |
0 |
0 |
28 |
53 |
70 |
90 |
106 |
120 |
133 |
| 100 |
15 |
15 |
43 |
68 |
85 |
105 |
121 |
135 |
| 200 |
25 |
25 |
53 |
78 |
95 |
115 |
131 |
| 300 |
40 |
40 |
68 |
93 |
110 |
130 |
| 400 |
50 |
50 |
78 |
103 |
120 |
| 500 |
62 |
62 |
90 |
115 |
| 600 |
73 |
73 |
101 |
| 700 |
82 |
82 |
Голубым цветом обозначен максимальный суммарный эффект от выделения соответствующего размера инвестиций 3-м предприятиям.
Таблица №5.
| m |
0 |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
| F3
(m) |
0 |
28 |
53 |
70 |
90 |
106 |
121 |
135 |
| z3
(m) |
0 |
0 |
0 |
0 |
0 |
0 |
100 |
100 |
В следующей таблице заполняем только одну диагональ для значения m = 700.
Таблица №6.
| m-x4
|
0 |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
| x4
|
f4
(x4
)/ F3
(m-x4
) |
0 |
28 |
53 |
70 |
90 |
106 |
121 |
135 |
| 0 |
0 |
0 |
28 |
53 |
70 |
90 |
106 |
121 |
135 |
| 100 |
20 |
20 |
48 |
73 |
90 |
110 |
126 |
141 |
| 200 |
33 |
33 |
61 |
86 |
103 |
123 |
139 |
| 300 |
42 |
42 |
70 |
95 |
112 |
132 |
| 400 |
48 |
48 |
76 |
101 |
118 |
| 500 |
53 |
53 |
81 |
106 |
| 600 |
56 |
56 |
84 |
| 700 |
58 |
58 |
| m |
0 |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
| F4
(m) |
0 |
28 |
53 |
73 |
90 |
110 |
126 |
141 |
| z4
(m) |
0 |
0 |
0 |
0 |
0 |
100 |
100 |
100 |
Сведем результаты в таблицу №7.
| m |
0 |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
| F1(m)=f1
(x1
) |
0 |
28 |
45 |
65 |
78 |
90 |
102 |
113 |
| z1=x1 |
0 |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
| F2
(m) |
0 |
28 |
53 |
70 |
90 |
106 |
120 |
133 |
| z2
(m) |
0 |
0 |
100 |
100 |
100 |
200 |
300 |
300 |
| F3
(m) |
0 |
28 |
53 |
70 |
90 |
106 |
121 |
135 |
| z3
(m) |
0 |
0 |
0 |
0 |
0 |
0 |
100 |
100 |
| F4
(m) |
0 |
28 |
53 |
73 |
90 |
110 |
126 |
141 |
| z4
(m) |
0 |
0 |
0 |
0 |
0 |
100 |
100 |
100 |
Теперь F4
(700)=141 показывает максимальный суммарный эффект по всем 4-м фирмам, а z4
(700)=100 - размер инвестиций в 4-ю фирму для достижения этого максимального эффекта. После этого на долю первых 3-х фирм осталось (700-100) и для достижения максимального суммарного эффекта по первым 3-м фирмам в 3-ю надо вложить 100 и т.д. Голубым цветом отмечены оптимальные значения инвестиций по фирмам и значения эффектов от них.
Таким образом, наилучшим является следующее распределение капитальных вложений по предприятиям: х1
*=300; х2
*=200; х3
*=100; х4
*=100. Оно обеспечивает производственному объединению наибольший возможный прирост прибыли 141 тыс.руб.
2. Анализ финансовых операций и инструментов.
Предположим, что ЛПР (Лицо, Принимающее Решения) обдумывает четыре возможных решения. Но ситуация на рынке неопределенна, она может быть одной из четырех. С помощью экспертов ЛПР составляет матрицу доходов Q. Элемент этой матрицы q[i,j] показывает доход, полученный ЛПР, если им принято i-е решение, а ситуация оказалась j-я. В этой ситуации полной неопределенности могут быть высказаны лишь некоторые соображения о том, какое решение принять. Сначала построим матрицу рисков. Строится эта матрица так: в каждом столбце матрицы доходов находим максимальный элемент d[j] , после чего элементы r[i,j]=d[j]-q[i,j] и образуют матрицу рисков.
Смысл рисков таков: если бы ЛПР знал что в реальности имеет место j-я ситуация, то он выбрал бы решение с наибольшим доходом, но он не знает, поэтому, принимая i-е решение он рискует недобрать d[j]-q[i,j] - что и есть риск.
матрица доходов
| Варианты (ситуации) |
max |
min |
Вальд |
Гурвиц: l*max+ +(1-l)*min; l=1/3 |
| Решения |
0 |
1 |
2 |
8 |
8 |
0 |
2,67 |
| 2 |
3 |
4 |
10 |
10 |
2 |
2 |
4,67 |
| 0 |
4 |
6 |
10 |
10 |
0 |
3,32 |
| 2 |
6 |
8 |
12 |
12 |
2 |
2 |
5,32 |
матрица рисков
| Варианты (ситуации) |
max |
Сэвидж |
| Решения |
2 |
5 |
6 |
4 |
6 |
| 0 |
3 |
4 |
2 |
4 |
| 2 |
2 |
2 |
2 |
2 |
| 0 |
0 |
0 |
0 |
0 |
0 |
Правило Вальда называют правилом крайнего пессимизма: ЛПР уверен, что какое-бы решение он ни принял, ситуация сложится для него самая плохая, так что, принимая i-е решение, он получит минимальный доход q[i]=min{q[i,j]:j=1..4}. Но теперь уже из чисел q[i] ЛПР выбирает максимальное и принимает соответствующее решение.
По правилу Сэвиджа находят в каждой строке матрицы рисков максимальный элемент r[i] и затем из чисел r[i] находят минимальное и принимают соответствующее решение.
По правилу Гурвица для каждой строки матрицы доходов находят величину z[i]=l*max{q[i,j]:j=1..4}+(1-l)*min{q[i,j]:j=1..4}, потом находят из чисел z[i] наибольшее и принимают соответствующее решение. Число l каждый ЛПР выбирает индивидуально - оно отражает его отношение к доходу и риску, при приближении l к 0 правило Гурвица приближается к правилу Вальда, при приближении l к 1 - к правилу розового оптимизма, в нашем случае l равно 1/3.
Итак, по правилу Вальда нам следует принять либо 2-ое, либо 4-ое решение. Сэвидж и Гурвиц нам советуют принять 4-ое решение.
Пусть теперь нам известны вероятности ситуаций - p[j]. Имея матрицу доходов Q теперь можно сказать, что доход от i-го решения есть с.в. Q[i] с доходами q[i,j] и вероятностями этих доходов p[j]. Кроме того, риск i-го решения также есть с.в. R[i] с рисками r[i,j] и вероятностями этих рисков p[j].
Тогда М(Q[i]), М(R[i]) - средний ожидаемый доход и средний ожидаемый риск i-го решения. Принимать решение (проводить операцию) нужно такое, у которого наибольший средний ожидаемый доход, или наименьший средний ожидаемый риск.
| Варианты (ситуации) |
М(Q[i]), М(R[i]) |
| Доходы |
0 |
1 |
2 |
8 |
2 |
| 2 |
3 |
4 |
10 |
4 |
| 0 |
4 |
6 |
10 |
4 |
| 2 |
6 |
8 |
12 |
6 |
| Риски |
2 |
5 |
6 |
4 |
4 |
| 0 |
3 |
4 |
2 |
2 |
| 2 |
2 |
2 |
2 |
2 |
| 0 |
0 |
0 |
0 |
0 |
| p[j] |
1/3 |
1/3 |
1/6 |
1/6 |
М(Q[i])= S(q[i,j]* p[j])М(R[i])= S (r[i,j]* p[j])
Голубым цветом выделен наибольший средний ожидаемый доход (4-ое решение), а красным цветом – наибольший средний ожидаемый риск (4-ое решение). Как видим, они соответствуют одному и тому же решения. Его и следует принять.
Операции: 1-я – (4;2), 2-я – (2;4), 3-я – (2;4), 4-я – (0;6).
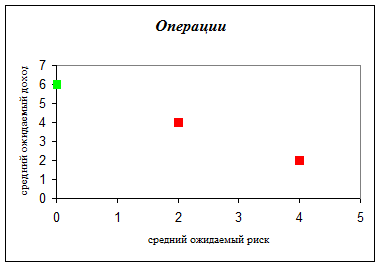
Красным цветом высвечены доминируемые точки (операции), а зеленым – недоминируемые, т.е. оптимальные по Парето. Оптимальной по Парето является 4-я операция.
Была проведена пробная операция, которая значительно сместила распределение вероятностей.
| Варианты (ситуации) |
М(Q[i]), М(R[i]) |
М*(Q[i]), М*(R[i]) |
| Доходы |
0 |
1 |
2 |
8 |
2 |
7,2 |
| 2 |
3 |
4 |
10 |
4 |
9,2 |
| 0 |
4 |
6 |
10 |
4 |
9 |
| 2 |
6 |
8 |
12 |
6 |
11 |
| Риски |
2 |
5 |
6 |
4 |
4 |
3,8 |
| 0 |
3 |
4 |
2 |
2 |
1,8 |
| 2 |
2 |
2 |
2 |
2 |
2 |
| 0 |
0 |
0 |
0 |
0 |
0 |
| p[j] |
1/3 |
1/3 |
1/6 |
1/6 |
| p*[j] |
0,1 |
0 |
0 |
0,9 |
Где p*[j] – вероятности после проведения пробной операции. М*(Q[i]), М*(R[i]) – средний ожидаемый доход и риск после проведения пробной операции.
Максимально оправданная стоимость пробной операции равна М*(Q[i]) - М(Q[i])=11 – 6 = 5.
Теперь выберем какие-нибудь две операции (1-ю и 4-ю), предположим, что они независимы друг от друга и найдем операцию, являющуюся их линейной комбинацией и более хорошую, чем какая-либо из имеющихся.
1-я операция = (4,2); 4-я операция = (0,6)
Результат: нельзя подобрать такой операции, являющейся линейной комбинацией 1-ой и 4-ой операции, которая бы доминировала все имеющиеся операции.
Пусть взвешивающая формула f(Q)=М[Q]/M[R], при M[R] не равным нулю, тогда для 1- 4 операций f1
=0,5; f2
=2; f3
=2; f4
= ¥. Следовательно 4-я операция является самой лучшей (max=¥), а 1-я – самая худшая.
Пусть доход от операции Q есть с.в., которую будем обозначать также как и саму операцию Q. Математическое ожидание M[Q]=S(q[i]*p[i]) называют еще средним ожидаемым доходом, а риск операции r = s=ÖD[Q]=Ö(M[Q2
]-M2
[Q]) отождествляют со средним квадратическим отклонением.
| номер операции |
Доходы (Q) и их вероятности (Р) |
M[Q] |
r |
| 1 |
0 |
1 |
5 |
14 |
4,2 |
5,19 |
| 1/5 |
2/5 |
1/5 |
1/5 |
| 2 |
2 |
4 |
6 |
18 |
6,8 |
5,74 |
| 1/5 |
2/5 |
1/5 |
1/5 |
| 3 |
0 |
8 |
16 |
20 |
8 |
8,72 |
| 1/2 |
1/8 |
1/8 |
1/4 |
| 4 |
2 |
12 |
18 |
22 |
16,25 |
6,12 |
| 1/8 |
1/8 |
1/2 |
1/4 |
Необходимые расчеты:
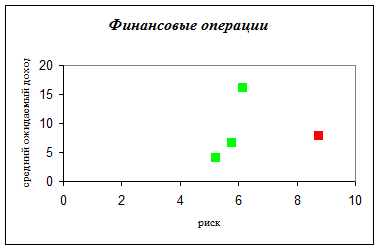
Красным цветом высвечены доминируемые точки (операции), а зеленым – недоминируемые, т.е. оптимальные по Парето. Оптимальными по Парето являются 1-я,2-я и 4-я операции.
Теперь выберем две операции (1-ю: Q1
и 4-ю: Q4
), предположим, что они независимы друг от друга и выясним, нет ли операции, являющейся их линейной комбинацией и более хорошей, чем какая-либо из имеющихся.
Пусть Q1
и Q4
две финансовые операции со средним ожидаемым доходом 4,2 и 16,25 и рисками 5,19 и 6,12 соответственно. Пусть t - какое-нибудь число между 0 и 1 . Тогда операция Qt=(1-t)Q1
+tQ4
называется линейной комбинацией операций Q1
,Q4
. Средний ожидаемый доход операции Qt равен M[Qt] = 4,2* (1-t) + 16,25*t, а риск операции Qt равен rt =Ö(26,94*(1-t)2
+37,44*t2
). Была найдена операция Q*, являющаяся линейной комбинацией исходных операций, со средним ожидаемым доходом 9,14 и риском 3,96, которая превосходит все имеющиеся операции по риску.
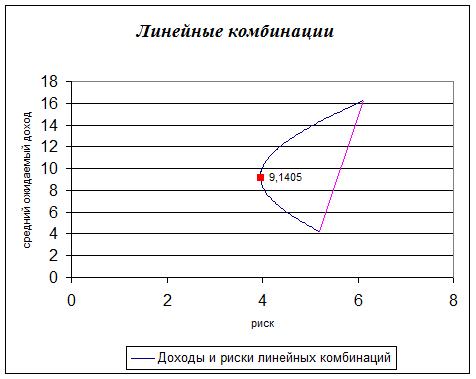
Определить лучшую и худшую операции можно также с помощью взвешивающей формулы f(Q)= 2*M[Q] – r. Имеем: f(Q1
)=3,21; f(Q2
)=7,86; f(Q3
)=7,28; f(Q4
)=26,38. Следовательно, 4-я операция является самой лучшей, а 1-я – самой худшей.
Исходные данные для анализа: ежедневные (суммарные) денежные вклады населения в отделение сбербанка в течение 4-х недель (или аналогичный какой-нибудь денежный поток).
Исходные данные:
| 1-я неделя |
2-я неделя |
3-я неделя |
4-я неделя |
| 1 |
2 |
3 |
4 |
5 |
6 |
1 |
2 |
3 |
4 |
5 |
6 |
1 |
2 |
3 |
4 |
5 |
6 |
1 |
2 |
3 |
4 |
5 |
6 |
| 6 |
5 |
13 |
15 |
14 |
13 |
9 |
9 |
9 |
9 |
9 |
9 |
12 |
12 |
12 |
12 |
12 |
12 |
3 |
1 |
17 |
19 |
5 |
4 |
Денежный поток:
| 6 |
5 |
13 |
15 |
14 |
13 |
9 |
9 |
9 |
9 |
9 |
9 |
12 |
12 |
12 |
12 |
12 |
12 |
3 |
1 |
17 |
19 |
5 |
4 |
Ранжированный ряд:
| 1 |
3 |
4 |
5 |
5 |
6 |
9 |
9 |
9 |
9 |
9 |
9 |
12 |
12 |
12 |
12 |
12 |
12 |
13 |
13 |
14 |
15 |
17 |
19 |
Дискретный вариационный ряд:
| значения |
1 |
3 |
4 |
5 |
6 |
9 |
12 |
13 |
14 |
15 |
17 |
19 |
| частоты |
1 |
1 |
1 |
2 |
1 |
6 |
6 |
2 |
1 |
1 |
1 |
1 |
| частости |
1/24 |
1/24 |
1/24 |
2/24 |
1/24 |
6/24 |
6/24 |
2/24 |
1/24 |
1/24 |
1/24 |
1/24 |
Многоугольник частот:
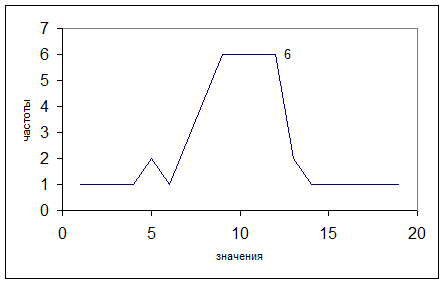
Интервальный вариационный ряд:
| Границы интервалов |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
| Середины интервалов |
1 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
| Частоты |
1 |
1 |
3 |
1 |
6 |
0 |
8 |
2 |
1 |
1 |
| Частости |
1/24 |
1/24 |
3/24 |
1/24 |
6/24 |
1/24 |
8/24 |
2/24 |
1/24 |
1/24 |
Многоугольник частостей:
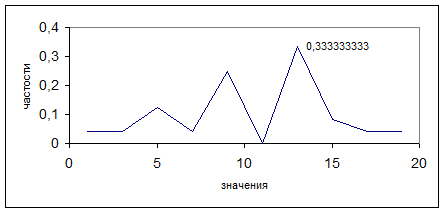
Выборочная функция распределения:
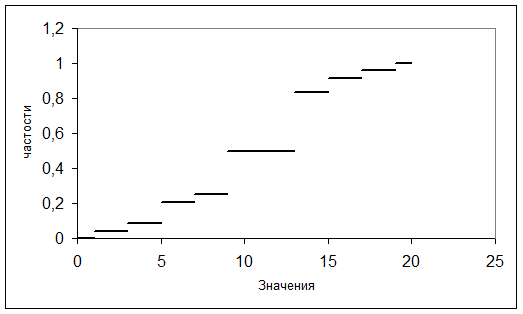
Статистические характеристики:
| По исходному ряду |
По дискретному ряду |
По интервальному ряду |
| Выборочная средняя |
10,4 |
10,4 |
10,42 |
| Выборочная дисперсия |
18,79 |
18,79 |
19,88 |
| Выборочное СКО |
4,33 |
4,33 |
4,46 |
| Несмещенная оценка ген. диспер. |
19,61 |
19,61 |
20,75 |
Необходимые формулы и расчеты:
3. Модели сотрудничества и конкуренции.
Рассмотрим две фирмы, i=1,2, выпускающие один и тот же товар. Пусть затраты i-й фирмы при выпуске x[i] равны a[i]*x[i] (таким образом, a[i] есть себестоимость выпуска одной единицы товара i-й фирмой). Произведенный обеими фирмами товар поступает на общий рынок. Цена на товар линейно падает в зависимости от поступающего на рынок общего его количества: p(x)=c-bx, c,b>0, где x=x[1]+x[2]. Следовательно, прибыль i-ой фирмы равна W[i](x[1],x[2])=x[i]*(c-bx)-a[i]*x[i]=bx[i]*(d[i]-(x[1]+x[2])),где d[i]=(с-a[i])/b. Поведение каждой фирмы определяется ее стремлением максимизировать свою прибыль.
Дано: a[1]=5, a[2]=6, b=9, c=77.
Тогда: p(x)=77-9*x d[1]=(с-a[1])/b=(77-5)/9=8 d[2]=(с-a[2])/b=(77-6)/9=7,89
W[1](x[1],x[2])= bx[1]*(d[1]-(x[1]+x[2]))= 9*x[1]*(8-(x[1]+x[2]))
W[2](x[1],x[2])= bx[2]*(d[2]-(x[1]+x[2]))= 9*x[2]*(7,89-(x[1]+x[2]))
Допустим, что первая фирма узнала стратегию второй, т.е. объем ее выпуска x[2]. Токда она выбрала бы свой выпуск из условия максимизации прибыли:
¶W[1]/ ¶x[1]= b*(d[1]-(x[1]+x[2])) – b* x[1]=0, т.е. x*[1]= (d[1]-x[2])/2=(8-x[2])/2
Аналогично для второй фирмы: x*[2]= (d[2]-x[1])/2=(7,89-x[1])/2
x*[2], x*[1] – оптимальные выпуски 1-ой и 2-ой фирм при условии, что они знают выпуск конкурента.
Теперь предположим, что производственные циклы фирм совпадают, т.е. a[1]=a[2]=5. Пуcть фирмы выбирают свои оптимальные выпуски, зная объем производства своего конкурента за прошлый период. Предположим, что d[1]/2<d[2]<2d[1], тогда эти прямые пересекаются в точке K с координатами x[1]=(2d[1]-d[2])/3, x[2]=(2d[2]-d[1])/3. Эта точка называется точкой Курно. Как видно на риссунке последовательность стратегий фирм сходится к этой точке. Так как а[1]=a[2], то d[1]=d[2]=8, тогда точка Курно K(d/3,d/3), x[i]=d/3, прибыли фирм W[i]=b*d2
/9, цена p=c-2*b*d/3. И еще одно условие x<=c/b<=d .
d[1]/2<d[2]<2d[1] - 8/2<8<2*8 - верно.
Нанесем на плоскость x [1] x[1] прямые-множества стратегий фирм в ответ на известную стратегию другой фирмы x*[1]=(8-x[2])/2 и x*[2]=(8-x[1])/2 и найдем точку их пересечения. x[1],х[2]=d/3=8/3=2,67. Далее определим прибыли фирм W[1], W[2]=b*d2
/9=9*64/9=64, p=c-2*b*d/3=77-2*9*8/3=29.
Теперь посмотрим, как действует модель Курно. Пусть 7,8 и 0,1 – выпуски фирм за прошлый год и каждая фирма знает этот выпуск своего конкурента. Тогда, зная его она применяет свою оптимальную стратегию с целью максимизировать прибыль. Убедимся, что после некоторого количества итераций они окажутся в точке Курно.
| N |
Выпуск |
Цена |
Прибыли |
| 1-я фирма |
2-я фирма |
1-я фирма |
2-я фирма |
| 0 |
7,8 |
0,1 |
| 1 |
3,95 |
0,1 |
40,55 |
140,42 |
3,56 |
| 2 |
2,99 |
2,03 |
31,89 |
80,33 |
54,45 |
| 3 |
2,75 |
2,51 |
29,72 |
64,93 |
62,09 |
Как видно уже при 3-ей операции выпуски и прибыли 1-ой и 2-ой фирмы и цена значительно приблизились к точке Курно. Посмотрим это графически.
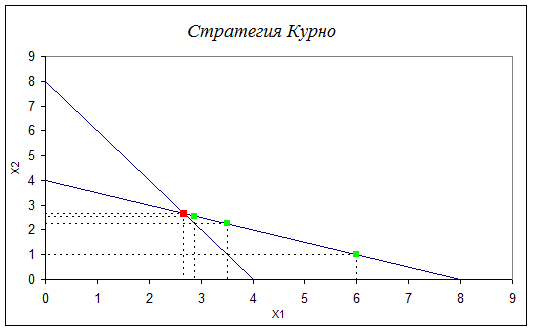
Зеленым цветом обозначены точки последовательных итераций, а красным – точка Курно.
Математической моделью конфликтов с двумя участниками являются биматричные игры. Такая игра 2х2 задается биматрицей (aij,bij) . В кооперативном варианте такой игры игроки могут согласованно выбирать элемент биматрицы. Если они выбрали элемент (a,b), то Первый игрок получает a , а Второй получает b . Цели игроков одинаковы - выиграть как можно больше в расчете на партию в среднем. Пусть (x,y), (a,b) - две точки из CE. Говорят, что (x,y) доминирует (a,b) если x>=a, y>=b и хотя бы одно из этих неравенств строгое. Недоминируемые точки называются оптимальными по Парето, а их множество - множеством оптимальности по Парето. Еще более узкое множество называется переговорным. Оно определяется так: пусть Vk - максимальный выигрыш, который k-й игрок может обеспечить себе при любой стратегии другого игрока, тогда переговорное множество определяется как множество тех точек множества Парето, у которых k-я координата не меньше Vk. Для нахождения Vk на до решить две задачи ЛП:
V1-->max, a11*x+a21*(1-x)>=V1,a11*x+a12*(1-x)>=V1, 0<=x<=1;
V2-->max, a11*y+a12*(1-y)>=V2,a21*y+a22*(1-y)>=V2, 0<=y<=1.
Дано:
биматрица
Нанесем на плоскость элементы биматрицы и начертим выпуклую оболочку.
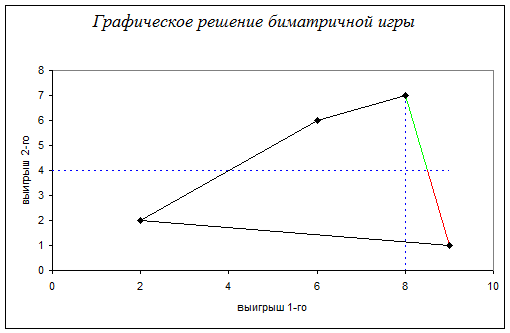
Где красным и зеленым цветом обозначено множество оптимальности по Парето, а зеленым – та его часть, которая является переговорным множеством. V1
=8, V2
=4.
Цена игры первого игрока V1
находится легко, так как в матрице аij
есть седловая точка а[2,1]=8. Основная теорема матричных игр утверждает, что для любой матричной игры max{min{M[P,Q]:Q}:P}=min{max{M[P,Q]:P}:Q}, т.е. во множестве смешанных стратегий есть седловая точка, дающая оптимальное решение игры. Поэтому V1
= а[2,1]=8, а оптимальная стратегия 1-го игрока Р*=(0 1), так как ему выгодно выбирать все время 2-ю строку.
Для того, чтобы найти цену игры и оптимальную стратегию 2-го игрока необходимо решить задачу ЛП. Если все разделить на V2 и сделать замену переменных, то получим:
V2-->max y/V2
=x1 x1 + x2 -min
2*y+6*(1-y)>=V2
, (1-y)/V2
=x2 2*x1 +6*x2>=1
7*y+1*(1-y)>=V2
, 7*x1 +1*x2>=1
0<=y<=1. x1, x2 ≥0
Решая ее находим V2
=4.
Итак, цена игры 2-го игрока V2
=4
4. Социально-экономическая структура общества.
Такой моделью является так называемая «диаграмма или кривая Лоренца».
Рассмотрим функцию распределения богатства в обществе d(z), которая сообщает, что z-я часть самых бедных людей общества владеет d(z)-й частью всего общественного богатства. Далее приведен график функции d(z). Площадь заштрихованной линзы называется коэффициентом Джинни J. Эта величина не более 1/2. Чем она меньше, тем равномернее распределено богатство в обществе. При J>0.2 распределение богатства называется опасно несправедливым - это преддверие социальных волнений. Из функции d(z) можно получить другую функцию w(z) , она сообщает долю общественного богатства, которой владеет z-я часть самых богатых людей (w(z)=1-d(1-z)). Еще одну функцию можно получить из d(z): S(x)=d(1/2+x)-S(1/2-x). Она показывает, что часть общества, которая богаче, чем (½-х) самых бедных, но беднее (½-х) самых богатых, владеет S(x)-й частью всего общественного богатства. График функции S расположен только над отрезком [0, 1/2]. Говорят, что в обществе есть средний класс, если d(3/4)-d(1/4)>=1/2 или, что то же самое S(1/4)>=1/2 .
Дано: d(z)= exp((7/2)*ln(z))
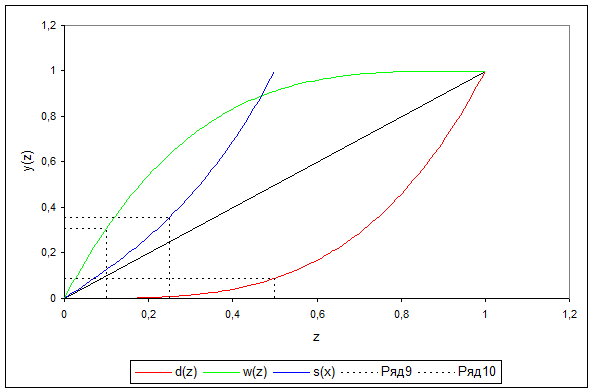
Как видно на графиках d(0,5)=0,09 ,т.е. половина самых бедных членов общества владеет только 9% всего общественного богатства. Вычислим коэффициент Джинни:
½ - J=( 0
∫1
(exp(7/2*ln(z)) dz)=0,22, значит J=0,28. Так как 0,28>0,2, то распределение богатства в обществе опасно несправедливо.
s(x)= exp((7/2)*ln(1/2+х)) - exp((7/2)*ln(1/2-х))
w(z)= 1 - exp((7/2)*ln(1-z))
Так как s(0,25)=0,36 и 0,36<0,5, то можно сделать вывод об отсутствии в данном обществе среднего класса. w(0,1)=0,31 означает, что десятая часть самых богатых владеет 31% всего общественного богатства.
Производные функций d(z) и w(z):
Пусть F(z) есть доля имеющих месячный доход меньше z по отношению ко всем, имеющим какой-нибудь денежный доход (всех таких членов общества назовем налогоплательщиками). Функцию F(z) вполне правильно трактовать как функцию распределения случайной величины I - месячный доход случайного налогоплательщика. С.в. I можно считать непрерывной. Функция F(z) может быть интересна налоговой инспекции. С помощью функции F(z) можно найти несколько интересных характеристик общества. Например, средний доход, который находится как интеграл от 0 до бесконечности функции z*dF(z). Другой подобной характеристикой является коэффициент Рейнбоу, который находится как отношение решений уравнений F(z)=0.9 и F(z)=0.1, т.е. этот коэффициент показывает отношение доходов 10% членов общества с самыми высокими доходами к доходам 10% с самыми низкими доходами. Если это отношение превышает 20, то распределение доходов называется несправедливым, иначе нормальным.
Дано: F(z)= 1 – exp(6*ln(500/(500+z)))
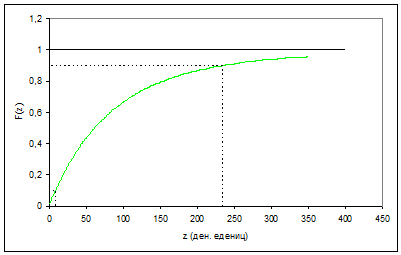
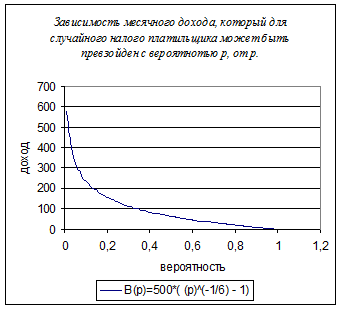
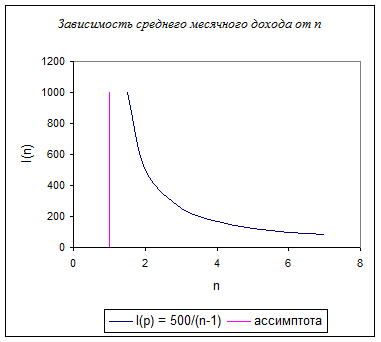
Как видно на графике 1, F(9)=0,1 и F(234)=0,9. Это говорит о том, что 10% низкодоходных членов общества имеют доход не более 9 у.е., а 10% высокодоходных имеют доход более 234 у.е. Если взять эти числа как отношение, то получим Коэффициент Рейнбоу. Так как 234/9=26 и 26>20, то распределение доходов в данном обществе можно считать несправедливым.
|