Криптографические способы защиты
1 Требования к шифрам
К шифрам, предназначенным для закрытия информации в ЭВМ и автоматизированных системах, предъявляется ряд требований, в том числе: достаточная стойкость (надежность закрытия), простота шифрования и расшифрования, независимость шифрования и расшифрования от способа внутримашинного представления информации, нечувствительность к небольшим ошибкам шифрования, возможность внутримашинной обработки зашифрованной информации, незначительная избыточность информации за счет шифрования и ряд других. В той или иной степени этим требованиям отвечают некоторые виды шифров замены, перестановки, гаммирования, а также шифры, основанные на аналитических преобразованиях шифруемых данных. Эти шифры рекомендуются зарубежными специалистами для использования с целью закрытия информации в автоматизированных системах.
2 Методы шифрования
2.1 Шифрование заменой (подстановкой)
В этом, наиболее простом методе символы шифруемого текста заменяются другими символами, взятыми из одного (одно- или моноалфавитная подстановка) или нескольких
(много- или полиалфавитная подстановка) алфавитов. Самой простой разновидностью является прямая замена, когда буквы шифруемого сообщения заменяются другими буквами того же самого или некоторого другого алфавита. Таблица замены может иметь следующий вид (таблица 1).
Таблица 1 - Таблица простой замены
| Символы шифруемого текста |
А
|
Б
|
В
|
Г
|
Д
|
Е
|
Ж
|
З
|
И
|
Й
|
К
|
Л
|
М
|
Н
|
О
|
П
|
| Заменяющие символы |
С |
П |
Х |
Л |
Р |
З |
Э |
М |
А |
Ы |
Я |
Д |
Ю |
Т |
Г |
Ж |
| Символы шифруемого текста |
Р
|
С
|
Т
|
У
|
Ф
|
Х
|
Ц
|
Ч
|
Ш
|
Щ
|
Ь
|
Ы
|
Ъ
|
Э
|
Ю
|
Я
|
| Заменяющие символы |
Н |
Й |
О |
Ц |
Б |
Ф |
У |
К |
Ч |
Ш |
Щ |
Ь |
И |
Ъ |
Е |
В |
Используя эту таблицу зашифруем слово криптография
. Получим: янажоглнсбав
. Однако, такой шифр имеет низкую стойкость. Зашифрованный текст имеет те же статистические характеристики, что и исходный. Поэтому простую замену в настоящее время используют редко и лишь в тех случаях, когда шифруемый текст короток.
Для повышения стойкости шифра используют так называемые полиалфавитные подстановки, в которых для замены символов используются символы нескольких алфавитов, причем смена алфавита осуществляется последовательно и циклически, то есть первый символ шифруемого текста заменяется первым символом соответствующего алфавита, второй - символом второго алфавита и т.д. до тех пор, пока не будут использованы все выбранные алфавиты. После этого использование алфавитов повторяется. Шифрование заменой в чистом его виде никогда не применяется, а всегда употребляется вместе с перестановкой, например, бит внутри байта.
Реклама

2.2 Шифрование методом перестановки
Этот метод заключается в том, что символы шифруемого текста переставляются по определенным правилам внутри шифруемого блока символов. Если после замены символы сообщения превращались во что угодно, но сохраняли в шифровке свое исходное местоположение, после перестановки они там расположены еще и где угодно, что надежно защищает шифровку от атак криптологов.
Простейшим примером перестановки является запись исходного текста по строкам некоторой матрицы, а чтение его по строкам этой матрицы. Последовательность заполнения строк и чтения столбцов может быть любой и задается ключом. Таким образом, для матрицы размерностью 8? 8 (длина блока 64 символа) возможно 1,6? 109
ключей, что позволяет на современных ЭВМ путем перебора расшифровать заданный текст. Однако для матрицы размерность 16? 16 (длина блока 64 символа) имеется 1,4? 1026
ключей и перебор их с помощью современных средств практически неосуществим.
Слабость шифрования простой перестановкой обуславливается тем, что при большой длине шифруемого текста в зашифрованном тексте могут появится закономерности символов ключа. Для устранения этого недостатка можно менять ключ после зашифровки определенного числа знаков. При достаточно частой смене ключа стойкость шифрования можно существенно повысить. При этом, однако, усложняется организация процесса шифрования и расшифрования.
Существуют более сложные методы перестановки. Усложнение перестановки по таблице заключается в том, что для записи символов шифруемого текста используется специальная таблица, в которую введены некоторые усложняющие элементы. Пример такой таблицы приведен на рисунке 1.
| ?
|
М |
Е |
Т |
О |
| Д |
_ |
П |
?
|
Е |
| Р |
?
|
Е |
С |
Т |
| А |
Н |
О |
?
|
В |
| К |
?
|
И |
_ |
_ |
Рисунок 1 Пример усложненной перестановки по таблице
Как следует из рисунка, таблица представляет собой матрицу размерами 5? 5 элементов (размеры могут быть выбраны произвольно), в которую, как и в случае простой перестановки, записываются знаки шифруемого текста. Усложнение состоит в том, что определенное число клеток таблицы не используется (на рисунке показаны знаком ?
). Количество и расположение неиспользуемых элементов является дополнительным ключом шифрования. Варьируя размерами таблицы, последовательностью символов ключа, количеством и расположением неиспользуемых элементов, можно получить требуемую стойкость зашифрованного текста.
Реклама

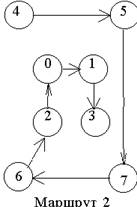
Весьма высокую стойкость шифрования можно обеспечить усложнением перестановок по маршрутам Гамильтона. При этом для записи символов шифруемого текста используются вершины некоторого гиперкуба, а знаки зашифрованного текста считываются по маршрутам Гамильтона, причем используется несколько различных маршрутов, например маршруты показанные на рисунке 2.
Из рассмотренных примеров очевидно, что все процедуры шифрования и расшифровки по методу перестановок являются в достаточной степени формальными и могут быть реализованы алгоритмически.
 Вскрытие случайной перестановки без знания ключа неоднозначно, что не позволяет сколь - нибудь уверенно расшифровать сообщение. Однако по сохранившейся статистике использованных в сообщении символов можно делать более или, скорее, менее уверенные прогнозы о его общем содержании. Вскрытие случайной перестановки без знания ключа неоднозначно, что не позволяет сколь - нибудь уверенно расшифровать сообщение. Однако по сохранившейся статистике использованных в сообщении символов можно делать более или, скорее, менее уверенные прогнозы о его общем содержании.
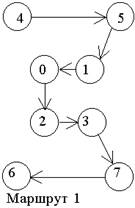 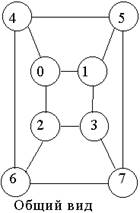
Рисунок 2 - Вариант схемы маршрутов Гамильтона
2.3 Шифрование с помощью датчика псевдослучайных чисел
Принцип зашифрования заключается в генерации гаммы шифра с помощью датчика псевдослучайных чисел (ПСЧ) и наложении полученной гаммы (гаммирование) на открытые данные обратимым образом (например, при использовании логической операции “исключающее ИЛИ”).
Процесс расшифрования данных сводится к повторной генерации гаммы шифра при известном ключе и наложению такой гаммы на зашифрованные данные. Полученный зашифрованный текст является достаточно трудным для раскрытия в том случае, когда гамма шифра не содержит повторяющихся битовых последовательностей. По сути дела гамма шифра должна изменяться случайным образом для каждого шифруемого слова. Фактически период гаммы превышает длину всего зашифрованного текста и неизвестна никакая часть исходного текста, а шифр можно раскрыть только прямым перебором (подбором ключа). В этом случае криптостойкость определяется размером ключа.
2.4 Шифрование аналитическим преобразованием
Смысл данного метода заключается в том, что шифруемый текст преобразуется по некоторому аналитическому правилу (формуле). Можно, например, использовать правило умножения матрицы на вектор, причем умножаемая матрица является ключом шифрования (поэтому ее размер и содержание должны сохраняться в тайне), а символами умножаемого вектора последовательно служат символы шифруемого текста. Расшифрование осуществляется с использованием того же правила умножения матрицы на вектор, только в качестве основы берется матрица, обратная той, с помощью которой осуществляется закрытие, а в качестве вектора - сомножителя - соответствующее количество символов закрытого текста. Данный метод легко реализуется программными средствами.
2.5 Комбинированные методы
Одним из важнейших требований, предъявляемых к системе шифрования, является ее высокая стойкость. Однако повышение стойкости любого метода шифрования приводит, как правило, к существенному усложнению самого процесса шифрования и увеличению затрат ресурсов (времени, аппаратных средств, уменьшению пропускной способности и т.п.).
Достаточно эффективным средством повышения стойкости шифрования является комбинированное использование нескольких различных способов шифрования, т.е. последовательное шифрование исходного текста с помощью двух или более методов. Считается, что при этом стойкость шифрования превышает суммарную стойкость составных шифров .
Вообще говоря, комбинировать можно любые методы шифрования и в любом количестве, однако на практике наибольшее распространение получили следующие комбинации:
1) подстановка + гаммирование;
2) перестановка + гаммирование;
3) гаммирование + гаммирование;
4) подстановка + перестановка.
Типичным примером комбинированного шифра является национальный стандарт США криптографического закрытия данных (DES).
2.5.1 Стандарт DES
Одним из наиболее распространенных криптографических стандартов на шифрование данных, применяемых в США, является DES (Data Encryption Standard). Первоначально метод, лежащий в основе данного стандарта, был разработан фирмой IBM для своих целей. Он был проверен Агентством Национальной Безопасности (АНБ) США, которое не обнаружило в нем статистических или математических изъянов. Это означало, что дешифрование данных, защищенных с помощью DES, не могло быть выполнено статистическими (например, с помощью частотного словаря) или математическими (“прокручиванием” в обратном направлении) методами.
После этого метод фирмы IBM был принят в качестве федерального стандарта. Стандарт DES используется федеральными департаментами и агентствами, для защиты всех достаточно важных данных в компьютерах (исключая некоторые данные, методы защиты которых определяются специальными актами). Его применяют многие негосударственные институты, в том числе большинство банков и служб обращения денег. Оговоренный в стандарте алгоритм криптографической защиты данных опубликован для того, чтобы большинство пользователей могли использовать проверенный и апробированный алгоритм с хорошей криптостойкостью. С одной стороны, публикация алгоритма нежелательна, поскольку может привести к попыткам дешифрования закрытой информации. Но, с другой стороны, это не столь существенно (если стандарт сильный) по сравнению со слабыми методами защиты данных, используемыми государственными институтами. Иначе говоря, потери от публикации алгоритма криптографической защиты намного меньше, чем потеря от применения методов с низкой криптостойкостью. Разумеется, стандартный алгоритм шифрования данных должен обладать такими характеристиками, чтобы его опубликование не сказалось на криптостойкости.
Суть алгоритма (алгоритм разработан для блока данных длиной 64 бит) заключается в преобразовании, которое состоит из серии перестановок (правая половина блока становится левой половиной “следующего” блока), операций запутывания (из правой половины блока длиной 32 бит формируется код длиной 48 бит, а каждый бит ключа размножается и превращается в подключ длиной 48 бит) и логических операций (с помощью функций ИСКЛЮЧАЮЩЕЕ ИЛИ производится обработка кода длиной 48 бит и подключа такой же длины, затем из получившегося сегмента длиной 48 бит выбираются 32 бит и, наконец, с помощью функции ИСКЛЮЧАЮЩЕЕ ИЛИ производится совместная обработка отобранных на втором этапе 32 бит и левой половины блока длиной 32 бит). Этот процесс перестановок в половине блока, повторных операций запутывания и многократных логических операций выполняется 16 раз, так как ключ состоит из 16 бит, каждый из которых генерирует 16 подключей (за счет выполнения операций запутывания).
Недостатки метода в малой длине блока и ключа, что недостаточно для таких задач, как национальная безопасность. Свое развитие DES получил в ГОСТ 281478-89 (отечественный стандарт на шифрование данных), который увеличил длину ключа до 256 бит и допустил произвольные перестановки.
2.6 Шифры с открытым ключом
Наиболее перспективными системами криптографической защиты данных являются системы с открытым ключом. В таких системах для зашифрования данных используется один ключ, а для расшифрования другой. Первый ключ не является секретным и может быть опубликован для использования всеми пользователями системы, которые зашифровывают данные. Расшифрование данных с помощью известного ключа невозможно. Для расшифрования данных получатель зашифрованной информации использует второй ключ, который является секретным. Разумеется, ключ расшифрования не может быть определен из ключа зашифрования. Системы с открытым ключом применяются, главным образом, в системах передачи данных по линиям связи большой протяженности.
2.6.1 Шифр Райвеста - Шамира - Алдемана
Первой и наиболее известной криптографической системой с открытым ключом была предложенная в 1978 году так называемая система RSA. Ее название происходит от первых букв фамилий авторов Rivest, Shamir и Aldeman, которые придумали ее во время совместных исследований в массачусетском технологическом институте в 1977 году. Она основана на трудности разложения очень больших целых чисел на простые сомножители. Международная сеть электронного перечисления платежей SWIFT уже требует от банковских учреждений, пользующихся ее услугами, применения именно этой криптографической системы. Алгоритм ее работает так :
1. Отправитель выбирает два очень больших простых числа P и Q и вычисляет два произведения N=PQ и
M=(P-1)(Q-1).
2. Затем он выбирает случайное целое число D, взаимно простое с М, и вычисляет Е, удовлетворяющее условию
DE=1 MOD M.
3. После этого он публикует D и N как свой открытый ключ шифрования, сохраняя Е как закрытый ключ.
4. Если S - сообщение, длина которого, определяемая по значению выражаемого им целого числа, должна быть в интервале (1,N), то оно превращается в шифровку возведением в степень D по модулю N и отправляется получателю
S’=SD
MOD N.
5. Получатель сообщения расшифровывает его, возводя в степень Е по модулю N, так как
S=S’E
MOD N=SDE
MOD N.
Где под простым числом понимается такое число, которое делится только на 1 и на само себя. Взаимно простые числа - числа, которые не имеют ни одного общего делителя кроме 1.
Результат операции i
mod j
- остаток от целочисленного деления i
на j
.
Таким образом, открытым ключом служит пара чисел N и D, а секретным ключом число Е. Смысл этой системы шифрования становится понятным, если упомянуть про малую теорему Ферма, которая утверждает, что при простом числе Р и любом целом числе К, которое меньше Р, справедливо тождество
KP-1
=1 MOD P.
Эта теорема позволяет определять, является ли какое-либо число простым или же составным.
Например выберем (для простоты малые) простые числа Р=211 и Q=223. В этом случае N=47053 и М=46620. Выберем открытый ключ шифрования D=16813 и вычислим секретный ключ расшифрования Е=19837. Теперь, взяв за сообщение название метода RSA, переведем его в число. Для этого будем считать букву R равной 18, S равной 19, А раной 1 по порядковому номеру их положения в английском алфавите. На представление каждой буквы отведем по 5 бит числа, представляющего открытый текст. В этом случае слову RSA соответствует следующее число:
S=((1*32)+19)*32+18=1650
С помощью открытого ключа получаем шифровку:
S’=SD
MOD N=165016813
MOD 47053=3071
Получатель расшифровывает ее с помощью секретного ключа:
S=S’E
MOD N=307119837
MOD 47053=1650
Криптостойкость системы RSA основана на том, что М не может быть просто вычислена без знания простых сомножителей P и Q , а нахождение этих сомножителей из N считалась трудно разрешимой задачей. Однако недавние работы по разложению больших чисел на сомножители показали, что для этого могут быть использованы разные и даже самые неожиданные средства. Сначала авторы RSA предлагали выбрать простые числа P и Q случайно, по 50 десятичных знаков каждое. Считалось, что такие большие числа очень трудно разложить на простые сомножители при криптоанализе. Райвест полагал, что разложение на простые множители такого числа (около 130 десятичных цифр) потребует более 40 квадриллионов лет машинного времени. Но математики Ленстра из фирмы Bellcore и манасси из фирмы DEC разложили число из 155 десятичных цифр на простые сомножители всего за 6 недель, соединив для этого 1000 ЭВМ, находящихся в разных странах мира.
2.6.2 Шифр ЭльГамаля
Криптографы постоянно вели поиски более эффективных систем открытого шифрования, и в 1985 году ЭльГамаль предложил следующую схему на основе возведения в степень по модулю большого простого числа. Для этого задается большое простое число Р
. Сообщения представляются целыми числами S
из интервала (1, Р). Оригинальный протокол передачи сообщения выглядит в варианте Шамира, одного из авторов RSA, так:
1. Отправитель А
и получатель В
знают лишь Р
. А
генерирует случайное число Х
из интервала (1, Р) и В
тоже генерирует случайное число Y
из того же интервала.
2. А
шифрует сообщение S1
=SX
MOD P и посылает В
.
3. В
шифрует его своим ключом S2
=S1
Y
MOD P и посылает S2
к А
.
4. А
“снимает” свой ключ S3
=S2
-X
MOD P и возвращает S3
к В
.
5. Получатель В
расшифровывает сообщение:
S=S3
-Y
MOD P.
В системе ЭльГамаля большая степень защиты, чем у алгоритма RSA достигается с тем же по размеру N, что позволяет почти на порядок увеличить скорость шифрования и расшифрования. Криптостойкость системы ЭльГамаля основана на том, что можно легко вычислить степень целого числа, то есть произвести умножение его самого на себя любое число раз так же, как и при операциях с обычными числами. Однако трудно найти показатель степени, в которую нужно возвести заданное число, чтобы получить другое тоже заданное. В общем случае эта задача дискретного логарифмирования кажется более трудной, чем разложение больших чисел на простые сомножители, на основании чего можно предполагать, что сложности вскрытия систем RSA и ЭльГамаля будут сходными. С точки зрения практической реализации, как программным, так и аппаратным способом ощутимой разницы между этими двумя стандартами нет. Однако в криптостойкости они заметно различаются. Если рассматривать задачу разложения произвольного целого числа длиной в 512 бит на простые сомножители и задачу логарифмирования целых чисел по 512 бит, вторая задача, по оценкам математиков, несравненно сложнее первой. Однако есть еще одна особенность. Если в системе, построенной с помощью алгоритма RSA, криптоаналитику удалось разложить открытый ключ N одного из абонентов на два простых числа, то возможность злоупотреблений ограничивается только этим конкретным пользователем. В случае же системы, построенной с помощью алгоритма ЭльГамаля, угрозе раскрытия подвергнуты все абоненты криптографической сети.
2.7 Сравнение основных криптографических методов
Метод шифрования с использованием датчика ПСЧ наиболее часто используется в программной реализации системы криптографической защиты данных. Это объясняется тем, что с одной стороны, он достаточно прост для программирования, а с другой стороны позволяет создавать алгоритмы с очень высокой криптостойкостью. Кроме того, эффективность данного метода шифрования достаточно высока. Системы основанные на методе шифрования с использованием датчика ПСЧ, позволяют зашифровать в секунду от нескольких десятков до сотен килобайт данных (здесь и в дальнейшем все характеристики приведены для персональных компьютеров).
Однако простота метода может сыграть злую шутку с разработчиком собственного алгоритма шифрования данных. Очень грозно выглядящий шифр может быть чувствителен к простым воздействиям. Поэтому каждый новый алгоритм шифрования данных перед его применением должен быть подвергнут всестороннему математическому, статистическому и криптографическому анализам. Только после устранения всех слабых сторон алгоритма он может использоваться для шифрования данных. В противном случае, результаты могут быть катастрофическими.
Основным преимуществом метода DES является то, что он является стандартом. Как утверждает Национальное Бюро Стандартов США алгоритм обладает следующими свойствами;
1. высокий уровень защиты данных против дешифрования и возможной модификации данных;
2. простота в понимании;
3. высокая степень сложности, которая делает его раскрытие дороже получаемой при этом прибыли;
4. метод защиты основывается на ключе и не зависит ни от какой “секретности” алгоритма;
5. Экономичен в реализации и эффективен в быстродействии.
Важной характеристикой этого алгоритма является его гибкость при реализации и использовании в различных приложениях обработки данных. Каждый блок данных шифруется независимо от других, что позволяет расшифровать отдельный блок в зашифрованном сообщении и структуре данных. Поэтому можно осуществить независимую передачу блоков данных и произвольный доступ к блокам данных. Ни временная, ни позиционная синхронизация для операций шифрования не нужна.
Алгоритм вырабатывает зашифрованные данные, в которых каждый бит является функцией от всех битов открытых данных и всех битов ключа. Различие лишь в одном бите данных дает в результате равные вероятности изменения для каждого бита зашифрованных данных.
Конечно, эти свойства DES выгодно отличают его от метода шифрования с использованием датчика ПСЧ, поскольку большинство алгоритмов шифрования, построенных на основе датчиков ПСЧ, не характеризуются всеми преимуществами DES. Однако и DES обладает рядом недостатков.
Самым существенным недостатком DES специалисты признают размер ключа, который считается слишком малым. Стандарт в настоящем виде не является неуязвимым, хотя и
очень труден для раскрытия (до сих пор не были зарегистрированы случаи дешифрования информации, зашифрованной с использованием метода DES). Для дешифрования информации методом подбора ключей достаточно выполнить 256
операций расшифрования (т.е. всего около 7? 1016
операций). Хотя в настоящее время нет аппаратуры, которая могла бы выполнить в обозримый период времени подобные вычисления, никто не гарантирует, что она не появится в будущем. Некоторые специалисты предлагают простую модификацию для устранения этого недостатка: исходный текст Р зашифровывается сначала по ключу К1, затем по ключу К2 и, наконец, по ключу К3. В результате время, требующееся для дешифрования, возрастает до 2168
операций (приблизительно, до 1034
операций).
Еще один недостаток метода DES заключается в том, что отдельные блоки, содержащие одинаковые данные (например, пробелы), будут одинаково выглядеть в зашифрованном тексте, что с точки зрения криптоанализа неправильно.
Метод DES может быть реализован программно. В зависимости от быстродействия и типа процессора персонального компьютера программная Среда, шифрующая данные с использованием метода DES, может обрабатывать от нескольких килобайт до десятков килобайт данных в секунду.
Алгоритм криптографического преобразования, являющийся отечественным стандартом и определяемый ГОСТ 28147-89, свободен от недостатков стандарта DES и в то же время обладает всеми его преимуществами. Кроме того, в стандарт уже заложен метод, с помощью которого можно зафиксировать необнаруженную случайную или умышленную модификацию зашифрованной информации.
Однако у алгоритма есть очень существенный недостаток, который заключается в том, что его программная реализация очень сложна и практически лишена всякого смысла из-за крайне низкого быстродействия. По оценкам авторов, за одну секунду на персональном компьютере может быть обработано всего лишь несколько десятков (максимально сотен) байт данных, а подобная производительность вряд ли удовлетворит кого-либо из пользователей. Хотя сейчас уже разработаны аппаратные средства, реализующие данный алгоритм криптографического преобразования данных, которые демонстрируют приемлемую производительность (около 70 Кб/с для IBM PC AT с тактовой частотой 12 Мгц), все же складывается впечатление, что разработчики алгоритма совершенно не заботились об эффективности его программной реализации и о стоимости шифрования данных.
Теперь остановимся на методе RSA. Он является очень перспективным, поскольку для зашифрования информации не требуется передачи ключа другим пользователям. Это выгодно отличает его от всех вышеописанных методов криптографической защиты данных. Но в настоящее время к этому методу относятся с подозрительностью, поскольку в ходе дальнейшего может быть найден эффективный алгоритм определения делителей целых чисел, в результате чего метод шифрования станет абсолютно незащищенным. Кроме того, не существует строгого доказательства, что не существует другого способа определения секретного ключа по известному, кроме как определения делителей целых чисел.
В остальном метод RSA обладает только достоинствами. К числу этих достоинств следует отнести очень высокую криптостойкость, довольно простую аппаратную и программную реализацию. Правда, следует отметить, что использование этого метода для криптографической защиты данных неразрывно связано с очень высоким уровнем развития вычислительной техники.
|