Федеральное агентство по образованию
Государственное образовательное учреждение высшего
профессионального образования
Самарский государственный технический университет
Факультет автоматики и информационных технологий
Кафедра информационно-измерительной техники
Расчетно-пояснительная записка
к курсовой работе Оптимизация прямого поиска для определения минимума функции
n
переменных методом Нелдера-Мида.
по курсуСистемы автоматического проектирования
НормоконтрольПетрова Т. А.
Руководитель работы Хавлин О.В.
Студент Бромберг Е.Е.
Группа 5-АИТ-5
Срок выполнения ____________________________
Работа защищена с оценкой___________
г. Самара 2008
Реферат
Пояснительная записка содержит 16страниц, 5 рисунков и 2 источника.
ЭКСТРЕМУМ ФУНКЦИИ, БАЗИСНАЯ ТОЧКА, СИМПЛЕКС, ОТРАЖЕНИЕ, РАСТЯЖЕНИЕ, СЖАТИЕ, ДЛИНА ШАГА, МЕТОД НЕЛДЕРА-МИДА.
В пояснительной записке изложены основы прямого поиска для определения минимума функции n
переменных. Выбран метод оптимизации поиска Нелдера-Мида. В расчетной части метод Нелдера-Мида реализован программно, в среде TurboPascal, представлены блок схема алгоритма оптимизации, листинг программы.
| СОДЕРЖАНИЕ |
Введение……………………………………………………...
1
Метод Нелдера-Мида…………………………………...
2
Блок –схема алгоритма…………………………………..
3
Листинг программы……………………………………...
4
Список используемой литературы………………………
|
4
5
9
10
16
|
ВВЕДЕНИЕ
На разработку методов прямого поиска для определения минимума функции n
переменных было затрачено много усилий. Методы прямого поиска являются методами, в которых используются только значения функции. Один из наиболее надежных метод Нелдера-Мида, являющийся одним из самых эффективных, если 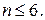
Рассмотрим функцию двух переменных. Ее линии постоянного уровня представлены на рис. 1. Линией постоянного уровня называется кривая в двухмерном сечении пространственных параметров ( в данном случае – в плоскости 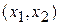 ), значение функции на которой константа. Минимум функции лежит в точке ), значение функции на которой константа. Минимум функции лежит в точке 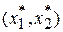 , где , где 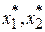 -где ряд значений от 0,1 до 1 с шагом 0,1. -где ряд значений от 0,1 до 1 с шагом 0,1.

1 МЕТОД НЕЛДЕРА-МИДА
Метод Нелдера-Мида является развитием симплексного метода Спендли, Хекста и Химсворта. Множество значений 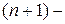 й равноудаленной точки в n
-
мерном пространстве называется регулярным симплексом. Эта конфигурация рассматривается в методе Спендли, Хекста и Химсворта. Следовательно, в двумерном пространстве симплексом является равносторонний треугольник, а в трехмерном пространстве – правильный тетраэдр. й равноудаленной точки в n
-
мерном пространстве называется регулярным симплексом. Эта конфигурация рассматривается в методе Спендли, Хекста и Химсворта. Следовательно, в двумерном пространстве симплексом является равносторонний треугольник, а в трехмерном пространстве – правильный тетраэдр.
Реклама

Идея метода состоит в сравнении значений функции в 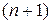 вершинах симплекса и перемещении симплекса в направлении оптимальной точки с помощью итерационной процедуры. В симплексном методе, предложенным первоначально, регулярный симплекс использовался на каждом этапе. Нелдер и Мид предложили несколько модификаций этого метода, допускающих, чтобы симплексы были неправильными. В результате получился очень надежный метод прямого поиска, являющийся одним из самый эффективных, если вершинах симплекса и перемещении симплекса в направлении оптимальной точки с помощью итерационной процедуры. В симплексном методе, предложенным первоначально, регулярный симплекс использовался на каждом этапе. Нелдер и Мид предложили несколько модификаций этого метода, допускающих, чтобы симплексы были неправильными. В результате получился очень надежный метод прямого поиска, являющийся одним из самый эффективных, если 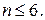
В данном методе симплекс перемещается с помощью трех основных операций: отражение, растяжение и сжатия. Рассмотрим основные шаги процедуры:
А. Найдем значения функции
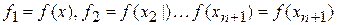
в вершинах симплекса.
Б. Найдем наибольшее значение функции 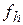 , следующее за набольшим значением функции , следующее за набольшим значением функции 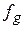 , наименьшее значение функции , наименьшее значение функции 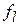 и соответствующие им точки и соответствующие им точки 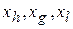 . .
В. Найдем центр тяжести всех точек, за исключением точки 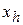 . Пусть центром тяжести будет . Пусть центром тяжести будет
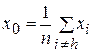
И вычислим 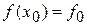 . .
Г. Удобнее всего начать перемещение от точки 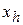 . Отразим точку . Отразим точку 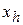 относительно точки относительно точки 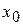 , получим точку , получим точку 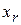 и найдем и найдем 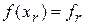 . .
Операция отражения иллюстрируется рис. 1. Если 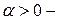 коэффициент отражения, то положение точки коэффициент отражения, то положение точки 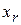 определяется следующим образом: определяется следующим образом:
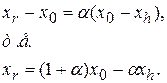

Д. Сравним значения функции 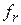 и и 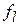 . .
1. Если 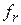 < <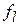 , то мы получим наименьшее значение функции. Направление из точки , то мы получим наименьшее значение функции. Направление из точки 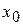 в точку в точку 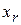 наиболее удобно для перемещения. Таким образом, мы производим растяжение в этом направлении и находим точку наиболее удобно для перемещения. Таким образом, мы производим растяжение в этом направлении и находим точку 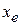 и значение и значение 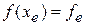 . Рисунок 2 иллюстрирует операцию растяжения симплекса. Коэффициент растяжения . Рисунок 2 иллюстрирует операцию растяжения симплекса. Коэффициент растяжения 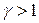 можно найти из следующих соотношений: можно найти из следующих соотношений:

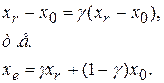
2. Если 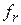 > >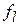 , но , но 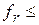 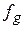 то то 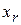 является лучшей точкой по с сравнению с другими двумя точками симплекса и мы заменяем точку является лучшей точкой по с сравнению с другими двумя точками симплекса и мы заменяем точку 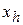 на точку на точку 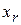 и, если сходимость не достигнута, возвращаемся на шаг Б. и, если сходимость не достигнута, возвращаемся на шаг Б.
3. Если 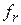 > >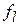 и и 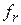 > >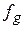 , то перейдите на шаг Е. , то перейдите на шаг Е.
Е. Сравним значения функции 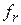 и и 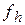 . .
1. Если 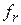 > >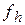 , то переходим непосредственно к шагу Е, 2. , то переходим непосредственно к шагу Е, 2.
Если 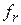 < <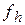 , то замещаем точку , то замещаем точку 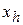 на точку на точку 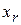 и значение функции и значение функции 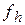 на значение на значение 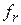 . Запоминаем значение . Запоминаем значение 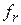 > >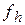 из шага Д,2. приведенного выше. Затем переходим на шаг Е, 2. из шага Д,2. приведенного выше. Затем переходим на шаг Е, 2.
2. В этом случае 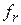 > >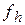 , поэтому ясно, что мы переместились далеко от точки , поэтому ясно, что мы переместились далеко от точки 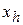 к точке к точке 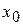 . Попытаемся исправить это, найдя точку . Попытаемся исправить это, найдя точку 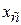 с помощью шага сжатия, показанного на рисунке 3. с помощью шага сжатия, показанного на рисунке 3.
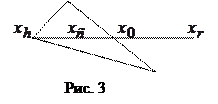
Если 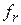 > >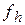 , то сразу переходим к шагу сжатия и находим точку , то сразу переходим к шагу сжатия и находим точку 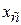 из соотношения: из соотношения:
Реклама

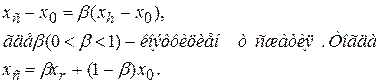
Если 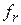 < <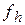 , то сначала заменим точку , то сначала заменим точку 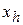 на точку на точку 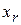 , а затем произведем сжатие. Тогда точку , а затем произведем сжатие. Тогда точку 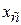 найдем из соотношения (см. рис.4): найдем из соотношения (см. рис.4):
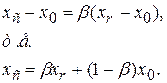
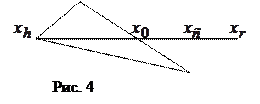
Коэффициенты 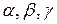 в вышеприведенной процедуре являются соответственно коэффициентами отражения, сжатия и растяжения. Нелдер и Мид рекомендуют брать в вышеприведенной процедуре являются соответственно коэффициентами отражения, сжатия и растяжения. Нелдер и Мид рекомендуют брать 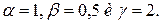
Рекомендация основана на результатах экспериментов с различными комбинациями значений. Эти значения параметров позволяют методу быть эффективным, но работать в различных сложных ситуациях.
В данной программе точка 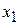 является начальной точкой, затем в программе формируются точки является начальной точкой, затем в программе формируются точки
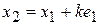
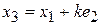
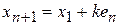
Где 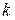 - произвольная длина шага, а - произвольная длина шага, а 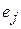 - единичный вектор. - единичный вектор.
Обозначения, используемые в программе, в целом соответствуют обозначениям, приведенным в тексте.
2 БЛОК – СХЕМА АЛГОРИТМА
Шаги этой процедуры представлены в виде блок-схемы алгоритма на рисунке 5.

3 ЛИСТИНГ ПРОГРАММЫ
Program Nidelermid;
Uses Crt;
Var n, i, j, g, h: integer;
S: array[1..10,1..10] of real;
x, xh,xg,xl,xo,xr,xc,xe: array[1..10] of real;
f: array[1..10] of real;
shag, l: integer;
al,be,ga: real;
k, fh, fl,fg,fo,fr,FE,fc,s1,s2,sig: real;
label 620,1520,1700,1920,2060,2200, 1300, 1600, 1440,2220;
function z(x1,x2,x3,x4: REAL): real;
begin
Z:=100*(x2-x1*x1)*(x2-x1*x1)+(1-x1)*(1-x1);
inc(shag);
end;
begin
clrscr;
shag:=0;
g:=1;
h:=1;
l:=1;
Writeln('Simpleksniy method Nidlera mida');
Writeln('Function: F(x)=100(x1-x2^2)^2+(1-x1)^2');
Writeln('Vvedite chislo peremennih');
Readln(n);
Writeln('Vvedite nachalnoe pribligenie');
for j:=1 to n do
readln(s[1,j]);
Writeln('Vvedite dlinny shaga');
Readln(k);
for i:=2 to n+1 do
for j:=1 to n do
if j=i-1 then
s[i,j]:=s[1,j]+k
else s[i,j]:=s[1,j];
Writeln('Vvedite Alfa, beta, gamma');
readln(al, be, ga);
for i:=1 to n+1 do
begin
for j:=1 to n do x[j]:=s[i,j];
f[i]:=z(x[1],x[2],x[3],x[4]);
end;
620:
fh:=-0.00000000000000000001;
fl:=0.00000000000000000001;
for i:=1 to n+1 do
begin
if f[i]>fh then
begin
fh:=f[i];
h:=i;
end;
if f[i]<fl then
begin
fl:=f[i];
l:=i;
end;
end;
fg:=0.00000000000000000001;
for i:=1 to n+1 do
if i<>h then
if f[i]>fg then
begin
fg:=f[i];
g:=i;
end;
for j:=1 to n do
begin
xo[j]:=0;
for i:=1 to n+1 do
if i<>h then xo[j]:=xo[j]+s[i,j];
xo[j]:=xo[j]/n;
xh[j]:=s[h,j];
xg[j]:=s[g,j];
xl[j]:=s[l,j];
end;
for j:=1 to n do x[j]:=xo[j];
fo:=z(x[1],x[2],x[3],x[4]);
writeln('Vichisliaem centr tiagest 1120');
for j:=1 to n do
begin
xr[j]:=xo[j]+al*(xo[j]-xh[j]);
x[j]:=xr[j];
end;
fr:=z(x[1],x[2],x[3],x[4]);
writeln('Vipolniaetsia otragenie 1220', z(x[1],x[2],x[3],x[4]):3:5);
if fr<fl then goto 1300;
if fr>fg then goto 1600;
goto 1520;
1300:
for j:=1 to n do
begin
xe[j]:=ga*xr[j]+(1-ga)*xo[j];
x[j]:=xe[j];
end;
fe:=z(x[1],x[2],x[3],x[4]);
if fe<fl then goto 1440;
goto 1520;
1440:
for j:=1 to n do s[h,j]:=xe[j];
f[h]:=fe;
Writeln('Vipolnite rastiagenie 1480', z(x[1],x[2],x[3],x[4]):3:5);
goto 2060;
1520:
for j:=1 to n do s[h,j]:=xr[j];
f[h]:=fr;
writeln('Vipolnenie otragenia 1560');
goto 2060;
1600:
if fr>fh then goto 1700;
for j:=1 to n do xh[j]:=xr[j];
f[h]:=fr;
1700:
for j:=1 to n do
begin
xc[j]:=be*xh[j]+(1-be)*xo[j];
x[j]:=xc[j];
end;
fc:=z(x[1], x[2],x[3],x[4]);
if fc>fh then goto 1920;
for j:=1 to n do s[h,j]:=xc[j];
f[h]:=fc;
writeln('Vipolnenie sjatia 1880', fc:3:5);
goto 2060;
1920:
for i:=1 to n+1 do
begin
for j:=1 to n do
begin
s[i,j]:=(s[i,j]+xl[j])/2;
x[j]:=s[i,j];
end;
f[i]:=z(x[1], x[2],x[3],x[4]);
end;
Writeln('Vipolnenie redikcii 2040');
2060:
s1:=0;
s2:=0;
for i:=1 to n+1 do
begin
s1:=s1+f[i];
s2:=s2+f[i]*f[i];
end;
sig:=s2-s1*s1/(n+1);
sig:=sig/(n+1);
if sig<0.000000001 then goto 2220;
2200:
goto 620;
2220:
Writeln('Minimum naiden v tochke f=', z(x[1],x[2],x[3],x[4]):3:5);
for j:=1 to n do Writeln('x',j,' =',xl[j]:3:5);
Writeln('Kolichestvo vichisleniy ravno ', shag);
readln;
end.
4 СПИСОКИСПОЛЬЗОВАННОЙЛИТЕРАТУРЫ
1. M.J. Box, D.Davies and W.H.Swann, “Non-linear Optimization Techniques
,” ICI Ltd Monograph No 5, Oliver and Boyd, 1969.
2. R.Hooke and T.A. Jeeves, “Direct search solution of numerical and statistical problem
”, 212-219, 1961.
|