Задания на контрольную работу.
1. Произвести моделирование случайной величины в ЕХСЕ
L
по варианту методом Монте-Карло.
1.1. С помощью функции c
лчи
c
заполнить таблицу требуемым количеством случайных величин, равномерно распределенных в интервале (0, 1).
1.2. В соответствии с заданным законом распределения рассчитать значения исследуемого показателя.
1.3. Скопировать значения исследуемого показателя как числа.
1.4. Упорядочить полученную статистику по возрастанию.
2. Произвести обработку статистических данных.
2.1. Оценивание методом моментов.
2.1.1. Рассчитать числовые характеристики: математическое ожидание, дисперсию, среднее квадратическое отклонение (стандартное отклонение), коэффициент вариации.
2.1.2. Рассчитать границы доверительного интервала для математического ожидания.
2.1.3. Рассчитать параметры закона распределения и сравнить их с заданными значениями, оценить относительную погрешность.
2.2. Сглаживание статистических данных.
2.2.1. Рассчитать и построить на одном графике эмпирическую и теоретическую функции распределения.
2.2.2. Сгруппировать статистические данные.
2.2.3. Рассчитать эмпирическую плотность распределения (гистограмму), теоретическую плотность распределения построить их на одном графике.
2.3. Проверка статистической гипотезы о законе распределения.
2.3.1. Проверить по критерию Колмогорова гипотезу о том, что закон распределения не противоречит статистическим данным.
2.3.2. Проверить по критерию Пирсона гипотезу о том, что законраспределения не противоречит статистическим данным.
3. Проанализировать полученные результаты и сделать выводы.
Таблица 1. Исходные данные по варианту.
| № вари-анта
|
Исследуемый показатель
|
Закон распределения
|
Параметры
закона распр.
|
Число
реализаций
|
| 18 |
Наработка между отказами контактной сети переменного тока межподстанционной зоны(ч) |
Вейбулла |
a=12800ч
b=3,4
|
180 |
1. Моделирование случайной величины в ЕХСЕ
L
методом Монте-Карло.
1.1. Заполнение таблицы требуемым количеством случайных величин (180), равномерно распределенных в интервале (0, 1).
Моделирование наработки между отказами контактной сети переменного тока межподстанционной зоны будем осуществлять с использованием генератора случайных чисел. Запускаем ЕХСЕ
L
, генерируем случайную величину в ячейке В2 с помощью мастера функций:
- левым щелчком мыши активируем ячейку В2;
- нажатием кнопки fx
вызываем мастера функций;
Реклама

- в категории «Математические» выбираем функцию СЛЧИС()

Рис.1 Выбор функции СЛЧИС().
- создаем массив значений (180 в соответствии с заданием) копированием формулы в другие ячейки массива, воспользовавшись автозаполнением:
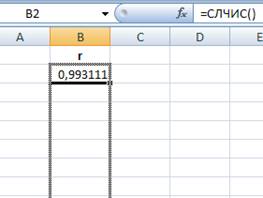
Рис. 2 Копирование формулы в ячейкиВ3:В182.
1.2. В соответствии с законом распределения Вейбулла рассчитаем значения исследуемого показателя - наработки между отказами контактной сети переменного тока межподстанционной зоны.
- активируем левым щелчком мыши ячейку С2;
- вводим формулу =
12800*(-LN(1-B2)^(1/3,4)
:

Рис. 3. Ввод формулы для расчета значений исследуемой величины.
- распространяем формулу в остальные ячейки, воспользовавшись автозаменой..
1.3. Копирование значений исследуемого показателя как числа.
Для дальнейшей обработки полученных значений необходимо освободиться от формул, т.е. получить массив числовых значений.
- выделяем полученный массив – ячейки С2:С182;
- с помощью кнопки «Копирование», отправляем значения массива в буфер обмена;
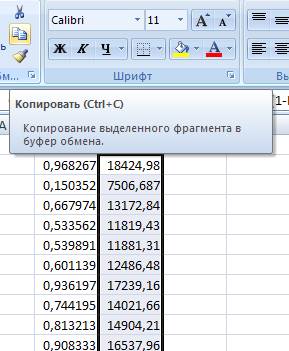
Рис. 4. Копирование массива в буфер обмена.
- активируем ячейку D2;
- правым щелчком мыши вызываем контекстное меню и выбираем команду «Специальная вставка»:
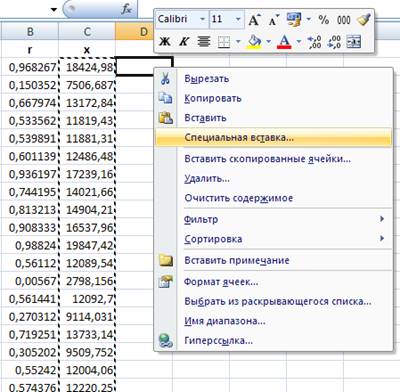
Рис. 5. Вызов контекстного меню и выбор команды «Специальная вставка».
- в появившемся диалоговом окне выбираем пункт «значения»:
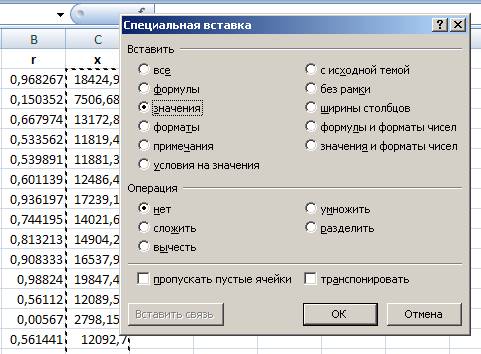
Рис. 6. Выбор вставки значения.
1.4. Упорядочение полученной статистики по возрастанию
.
Отсортируем полученный массив по возрастанию:
- выделяем диапазон D2:D182;
- выберем пункт меню ДАННЫЕ – СОРТИРОВКА, в появившемся окне включим радиокнопку «сортировать в пределах указанного выделения» и нажимаем кнопку «Сортировка…»:
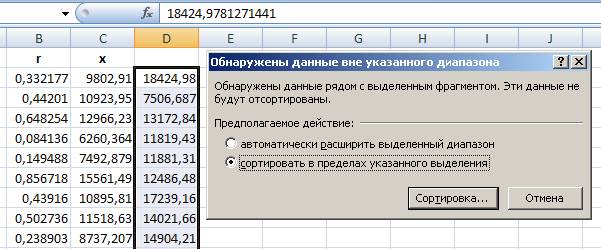
Рис. 7. Выбор диапазона для сортировки.
- в появившемся окне выберем сортировку по столбцу D и по возрастанию:
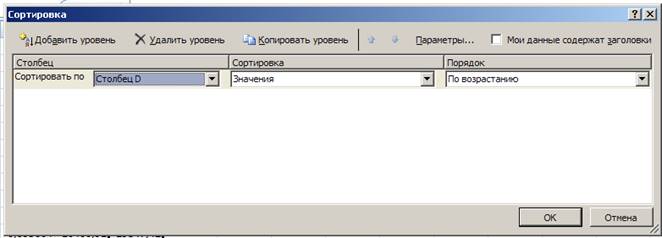
Рис. 8. Сортировка данных по возрастанию.
Получили статистику из 180 наблюдений – статистику длительности времени между наступлениями отказа контактной сети переменного тока межподстанционной зоны, отсортированную по возрастанию.
2. Обработка статистических данных.
Для выполнения следующих заданий скопируем полученные данные на ЛИСТ 2 в ячейки В4:В184.
2.1. Оценивание методом моментов.
2.1.1. Рассчитаем числовые характеристики:
- математическое ожидание,
- дисперсию,-
- среднее квадратическое отклонение (стандартное отклонение),
-коэффициент вариации.
Математическое ожиданиеопределим как среднее арифметическое
В ячейку С4 введем формулу:
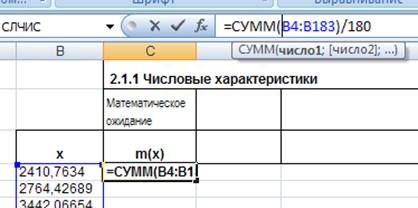
Рис. 9. Ввод формулы для расчета математического ожидания .
Реклама

Полученное значение m(x) = 11588,0159 говорит о том, что при 180 наблюдениях за наработкой на отказ контактной сети отказ её наступает в среднем после наработки примерно 11588 часов.
Оценим рассеяние случайной длительности наработки между отказами вокруг своего математического ожидания, т.е. найдем дисперсию. Для её расчета найдем сначала дисперсию отдельных слагаемыхпо формуле:
(х - m(x))^2
, для чего в ячейку D4 введем = (B4-$C$4)^2
, и распространим её для всего ряда, воспользовавшись автозаполнением:
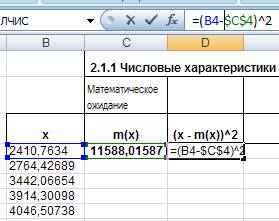
Рис. 10. Ввод формулы
Теперь вычислим дисперсию по формуле: σ2
=(∑(х - m(x))^2)/(n-1).
Для этого в ячейку Е4 введем формулу = СУММ(D4:D183)/(180-1):
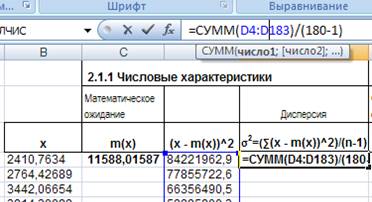
Рис. 11. Ввод формулы для расчета дисперсии.
Полученный результат σ2
= 13856179,2
используем для расчета среднего квадратичного отклонения (стандартного отклонения), которое равно корню квадратному дисперсии. В ячейку F4 вводим формулу = E4^(1/2):
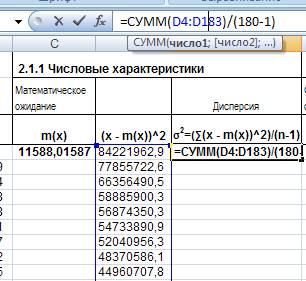
Рис. 12. Ввод формулы для расчета среднего квадратичного отклонения.
Коэффициент вариации случайной величины — мера относительного разброса случайной величины; показывает, какую долю среднего значения этой величины составляет ее средний разброс. Для её нахождения введём в ячейку G4 формулу =
F4/C4
(установим формат ячейки процентный):
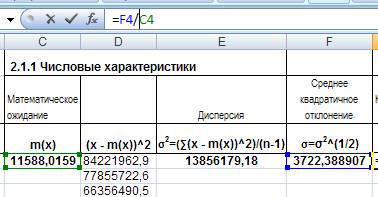
Рис. 13. Расчет коэффициента вариации.
Полученный коэффициент вариации показывает, что стандартное отклонение от среднего значения наработки на отказ контактной сети составляет 32,12%.
Результаты расчетов внесем в таблицу 2.1.
Таблица 2.1. Числовые характеристики
| Математическое ожидание |
Дисперсия |
Среднее квадратичное отклонение |
Коэффициент вариации |
| 11588,02 |
13856179,18 |
3722,39 |
32,12% |
2.1.2. Расчет границы доверительного интервала для математического ожидания.
Зная среднее квадратичное отклонение, для расчета доверительного интервала для математического ожидания воспользуемся встроенной функцией ExcelДоверит().
Примем доверительную вероятность 0,95. Активируем произвольно выбранную ячейку I4 для вставки функции. Вызовем Мастера функций, выполнив последовательность щелчков: Вставка®Формулы®Вставить функцию. В появившемся окне Мастера функций в окне «Поиск функции» введем «доверит» и щелкнем «Найти»:
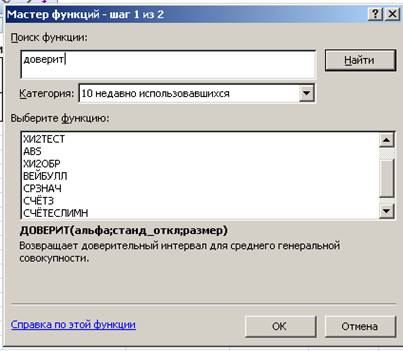
Рис. 14. Поиск функции Доверит().
Функция найдена и Мастер функции предложит ввести аргументы:
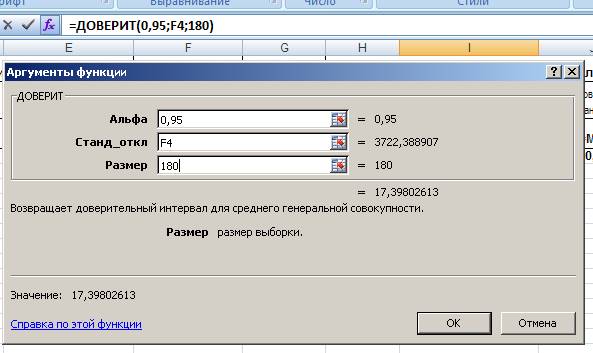
Рис. 15. Вставка функции Доверит().
Получили доверительный интервал для математического ожидания. Теперь рассчитаем нижнюю и верхнюю границы доверительного интервала по формулам: НДГ=
m
(х)-R
и ВДГ=
m
(х)+R
, где НДГ, ВДГ – соответственно нижняя и верхняя границы доверительного интервала, m(х) – математическое ожидание, R – доверительный интервал. Введем соответствующие формулы в ячейки J4 и K4:
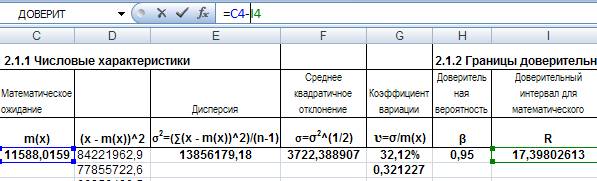
Рис. 16. Ввод формулы для расчета НДГ математического ожидания.
Аналогично введем формулу для расчета ВДГ в ячейку J4. Полученные результаты расчетов представлены в таблице 2.2.
Таблица 2.2. Границы доверительного интервала
для математического ожидания.
| Доверительный интервал для математического ожидания: |
Нижняя доверительная граница |
Верхняя доверительная граница |
| 17,39802613
|
11570,61785
|
11605,4139
|
2.1.3. Расчет параметров закона распределения, оценка относительной погрешности.
Для расчета параметров закона распределения будем использовать ранее вычисленное значение коэффициента вариации. Параметры найдем по формулам:
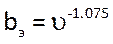 , ,
где: bэ
– эмпирический параметр b, υ – коэффициент вариации. Формулу введём в ячейку N4:
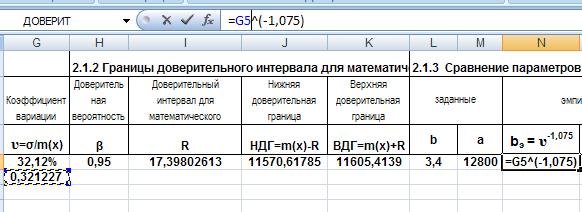
Рис. 17. Ввод формулы для расчета параметра
b
.
Параметр а находим по формуле:
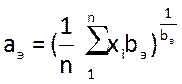 , ,
где: аэ
– эмпирический параметр а, n= 180 – объём выборки, xi
– случайное число (наработка на отказ). Для этого сначала в столбце Р рассчитаем произведения xi
∙bэ
: в ячейку Р4 введём формулу =B4^$N$4
, и распространим её на весь диапазон В4:В183
.
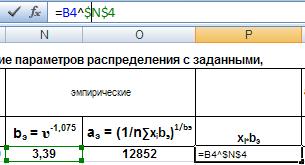
Рис. 18. Ввод формулы.
Теперь в ячейку О4 введем расчетную формулу для параметра а: =(СУММ(P4:P183)/180)^(1/N4)
:
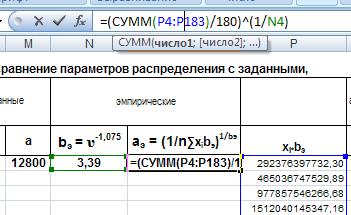
Рис. 19. Ввод формулы для расчета параметра а.
Переходим к оценке погрешностей. Сначала рассчитаем абсолютные погрешности:
аэ
– а
– для параметра а
, и bэ
– b
– для параметра b
.
Затем вычислим относительные погрешности по формулам:
(аэ
- а)/а
– для параметра а
, и (bэ
- b)/b
– для параметра b
.
Для этого в ячейки Q4, R4, S4,T4 соответственно введем формулы: =O4-M4, =L4-N4, =Q4/M4, =R4/L4
.
Для ячеек S4,T4 установим формат ячейки процентный: Формат ®Формат ячеек®Число®Процентный.
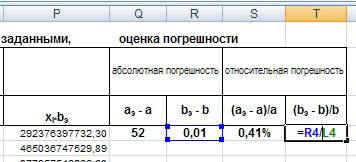
Рис. 20. Ввод формулы для расчета относительной погрешности
b
.
Результаты расчетов в сравнении с заданными сведем в таблицу 2.3.
Таблица 2.3.
Сравнение параметров распределения с заданными, оценка погрешности
| Заданные параметры |
Эмпирические параметры |
Абсолютная погрешность |
Относительная погрешность |
| а |
b |
аэ |
bэ |
а |
b |
а |
b |
| 3,4 |
12800 |
3,39 |
12852 |
52 |
0,01 |
0,41% |
0,29% |
2.2. Сглаживание статистических данных.
2.2.1. Расчет и построение графиков эмпирической и теоретической функции распределения.
Перейдем на ЛИСТ 3, для чего скопируем диапазон данных В4:В183 на ЛИСТ 3 в А4:А183.
На диапазоне ячеек В4:В183 расположим значения эмпирической функции распределения, а для теоретической – выделим диапазон С4:С183. Для расчета значений эмпирической функции распределения в ячейку В4 введем формулу =1/180
, а в ячейку В5 - =B4+1/180
, и распространим ее копированием на остальные ячейки выделенного диапазона.
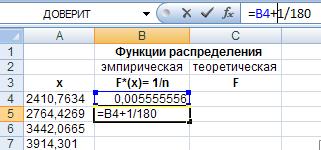
Рис. 21. Ввод формулы для расчета эмпирической функции распределения.
Для расчета теоретической функции распределения воспользуемся встроенной функцией ВЕЙБУЛЛ(). Для чего в ячейке С4 вызовем Мастера функций, найдем аналогично п.2.1.2 функцию ВЕЙБУЛЛ(). В появившемся окне введем аргументы функции:
- аргумент Х – случайное число (наработка на отказ),
- аргумент Альфа – параметр b = 3.4,
- аргумент Бета – параметр а = 12800,
- последний аргумент выбираем «интегральная», так как на данном этапе мы должны получить функцию распределения Вейбулла, а не Функцию плотности распределения Вейбулла.
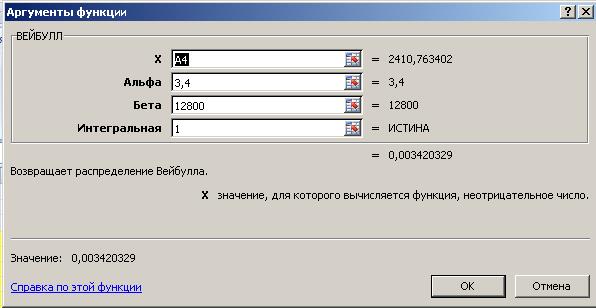
Рис. 22. Ввод аргументов функции ВЕЙБУЛЛ().
Распространим эту формулу на остальные ячейки выделенного диапазона автозаполнением.
Переходим к построению графиков функций. Выполним последовательность команд:
Вставка®Гистограмма®Все типы диаграмм®Точечная®Точечная с гладкими кривыми®ОК. Далее нажать «Выбрать данные», в появившемся диалоговом окне ввести:
- диапазон данных для диаграммы – диапазоны, которые мы выделили для функций распределения;
- Ряд1 ®Изменить эмпирическая;
- Ряд2® Изменить теоретическая, нажать ОК.
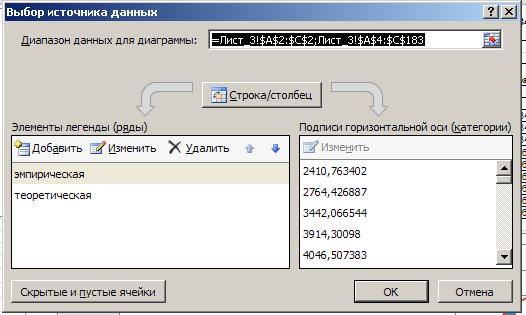
Рис. 23. Выбор источника данных для диаграммы.
Получим график, представленный на рисунке 24.
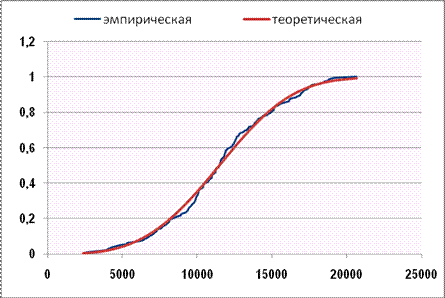
Рис. 24. Графики эмпирической и теоретической функций распределения.
2.2.2. Группировка статистических данных.
Сначала определим необходимое число групп (интервалов) по формуле Стерджесса:
k = 1+3,3222*lgn
k = 1+3,3222*lg180 = 8,492466316. Округляем до целого, т.е. k = 9.
Находим максимальное и минимальное значения случайной величины. Воспользуемся функциями МАКС() и МИН().
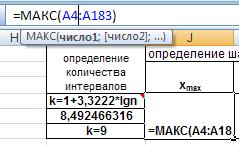 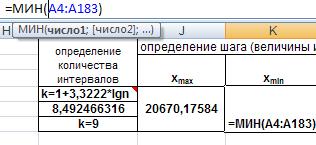
Рис. 25. Ввод функций МАКС() и МИН().
Теперь определяем шаг интервала по формуле:
h = (xmax
-xmin
)/k
.
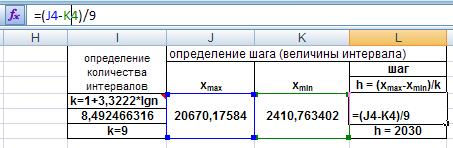
Рис. 26. Ввод формулы для расчета шага интервала.
Полученное значение округляем до целого: h = 2030.
Готовим таблицу для занесения группированных данных.Нижнюю и верхнюю границы каждого интервала найдем так. Нижняя граница первого интервала равна минимальному значению выборки. Добавим к ней шаг интервала и получим верхнюю границу интервала. Она же будет нижней границей второго интервала, верхнюю границу второго интервала получим так же, как и для первого. Так находим все границы. Записываем формулы в ячейки: K13, J14, K14 соответственно: =J13+2030, =K13, =J14+2030:
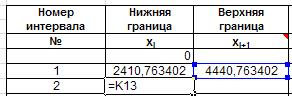 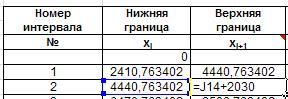
Рис. 27. Ввод формул для расчета границ интервалов
.
Распространяем формулы с ячеек K14 и J14 на остальные ячейки автозаполнением. Получим сгруппированные данные в таблице 2.4.
Таблица 2.4.
Сгруппированные статистические данные о наработке между отказами контактной сети.
| Номер интервала
|
Нижняя граница
|
Верхняя граница
|
| №
|
хi
|
хi+1
|
| 1 |
2410,763402 |
4440,763402 |
| 2 |
4440,763402 |
6470,763402 |
| 3 |
6470,763402 |
8500,763402 |
| 4 |
8500,763402 |
10530,7634 |
| 5 |
10530,7634 |
12560,7634 |
| 6 |
12560,7634 |
14590,7634 |
| 7 |
14590,7634 |
16620,7634 |
| 8 |
16620,7634 |
18650,7634 |
| 9 |
18650,7634 |
20679,58701 |
2.2.3. Расчет эмпирической плотности распределения (гистограммы), теоретической плотности распределения, построение графика.
Для нахождения эмпирической и теоретической плотностей распределения сначала рассчитаем частоты. Частота в каждой группе – это число отказов, имеющих значение меньше верхней границы, но не меньше нижней границы интервала. Исходя из этого, вводим формулы для расчета частот. На рисунке 28а и 28б показаны формулы для двух ячеек.
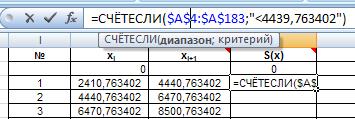
Рис. 28а. Ввод формулы для расчета частоты попадания СВ в первый интервал.
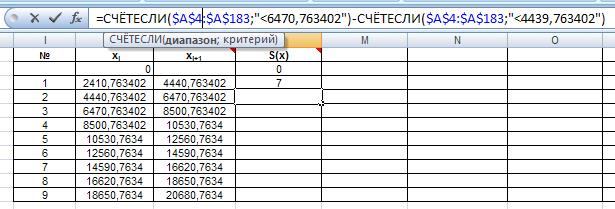
Рис. 28б. Ввод формулы для расчета частоты попадания СВ во второй интервал.
Аналогично вводим формулы для остальных интервалов. В сумме получим 180, значит формулы введены верно.
Определи частости по формуле:
Wi
(x)=S(x)/n
,
где S(x) – частоты каждого интервала. Введем формулу в ячейку М13 и распространим на остальные ячейки столбца автозаполнением (рис. 29).
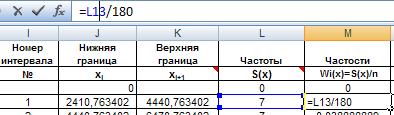
Рис. 29. Ввод формулы для расчета частости.
Частость – это вероятность попадания СВ в заданный интервал, поэтому мы получили, что сумма частостей равна 1.
Найдем середины интервалов как полусумму нижней и верхней границ интервалов:
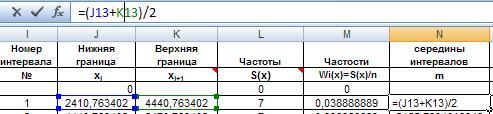
Рис. 30. Ввод формулы для определения середины интервала.
Находим эмпирическую плотность распределения по формуле:
f
*
=
S
(
x
)
/
(
n
*
h
)
?
где f
*
- эмпирическая плотность распределения, S
(
x
)
– частота, n
= 180, h
= 2030 – шаг интервала.
Введем формулу в ячейку О13 и распространим на остальные ячейки столбца.
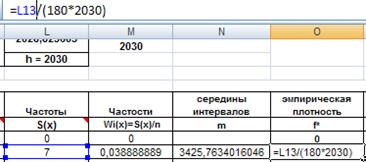
Рис. 31. Ввод формулы для расчета эмпирической плотности распределения.
Теоретическую плотность распределения найдем, воспользовавшись встроенной функцией ВЕЙБУЛЛ(). Аргументы вводим так же, как когда находили плотность распределения, только первым аргументом теперь будет середина интервала (ячейки столбца M), а последний – «дифференциальная»:
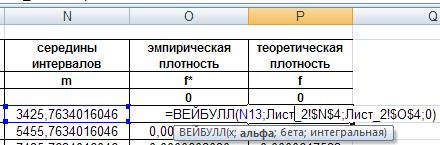
Рис. 32. Ввод функции ВЕЙБУЛЛ().
Полученные расчеты представлены в таблице 2.5.
Таблица 2.5.
Результаты расчета эмпирической и теоретической плотности распределения.
| Номер интервала |
Нижняя граница |
Верхняя граница |
Частоты |
Частости |
середины интервалов |
эмпирическая плотность |
теоретическая плотность |
| № |
хi
|
хi+1
|
S(х) |
Wi(x)=S(x)/n |
m |
f* |
f |
| 0 |
2410,763402 |
0 |
0 |
0 |
0 |
| 1 |
2410,763402 |
4440,763402 |
7 |
0,038888889 |
3425,76340160 |
0,0000191571 |
0,0000110622 |
| 2 |
4440,763402 |
6470,763402 |
7 |
0,038888889 |
5455,76340160 |
0,0000191571 |
0,0000322115 |
| 3 |
6470,763402 |
8500,763402 |
22 |
0,122222222 |
7485,76340160 |
0,0000602080 |
0,0000617523 |
| 4 |
8500,763402 |
10530,7634 |
35 |
0,194444444 |
9515,76340160 |
0,0000957854 |
0,0000896313 |
| 5 |
10530,7634 |
12560,7634 |
43 |
0,238888889 |
11545,7634016 |
0,0001176793 |
0,0001018574 |
| 6 |
12560,7634 |
14590,7634 |
26 |
0,144444444 |
13575,7634016 |
0,0000711549 |
0,0000901968 |
| 7 |
14590,7634 |
16620,7634 |
18 |
0,1 |
15605,7634016 |
0,0000492611 |
0,0000608259 |
| 8 |
16620,7634 |
18650,7634 |
17 |
0,094444444 |
17635,7634016 |
0,0000465244 |
0,0000302135 |
| 9 |
18650,7634 |
20680,7634 |
5 |
0,027777778 |
19665,7634016 |
0,0000136836 |
0,0000106194 |
| сумма |
180
|
1
|
Строим гистограмму эмпирической плотности распределения и график теоретической функции распределения на одном графике. Выполним последовательность команд:
Вставка®Гистограмма ®ОК. Далее нажать «Выбрать данные», в появившемся диалоговом окне ввести данные как показано на рисунке 33.
- Ряд1 ®Изменить на Эмпирическая;
- Ряд2® Изменить на Теоретическая;
- Подписи по горизонтальной оси выбрать верхние границы интервалов;
, нажать ОК.
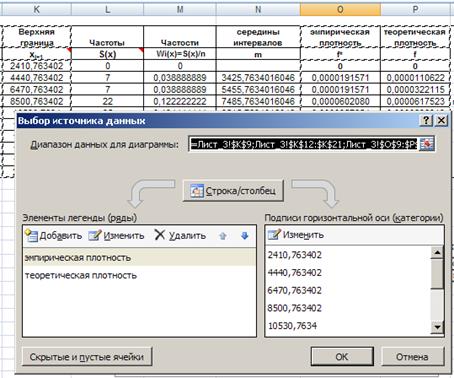
Рис. 33. Ввод данных для гистограммы.
Получим гистограмму, которая представлена на рисунке 34.
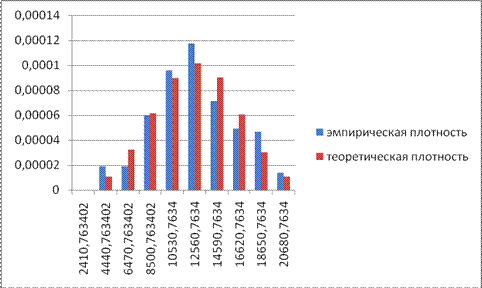
Рис. 34. Гистограмма плотностей распределения.
Чтобы получить график плотности теоретической распределения из гистограммы, щелкнем на гистограмме ряд с данными теоретической плотности распределения, вызвать контекстное меню и выбрать пункт «Изменить тип диаграммы для ряда»:
Рис. 35. Выбор изменения типа диаграммы для ряда.
Выбрать тип диаграммы «Точечная с гладкими кривыми». Далее выбрать Формат подписи данных по горизонтальной оси, и формат числа с числом десятичных знаков 0. Формат Легенду расположить в верхней части диаграммы. После этих преобразований получим график, как на рисунке 36.
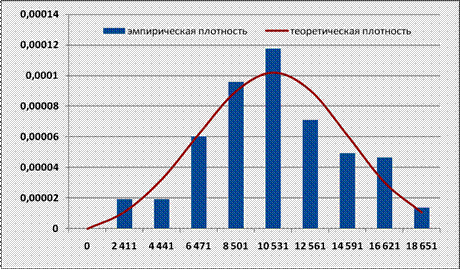
Рис. 36. Гистограмма эмпирической плотности распределения и график теоретической плотности распределения.
2.3. Проверка статистической гипотезы о законе распределения.
Гипотеза. Распределение исходных данных о наработке между отказами соответствует закону Вейбулла.
2.3.1.
Проверка по критерию Колмогорова гипотезы о том, что закон
распределения не противоречит статистическим данным.
Находим наибольшую разницу между эмпирической f*
(x
) и теоретической F
(x
) фyнкциями распределения:
D = max|F(xi
) – F*
(xi
)|, (i=1,2,…,k).
Для этого введем в ячейку D4 формулу для абсолютной разности f* и F, распространим на весь диапазон D4:D183. Затем в ячейке D184 найдем максимальную разность.
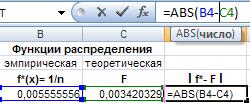 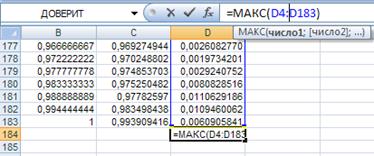
Рис. 37. Ввод формул для расчета наибольшей разности между эмпирической и теоретической функция ми распределения.
Получим: D =0,0494875066.
Находим статистику Колмогорова - величину 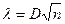 = 0,049499*√180= 0,66395. = 0,049499*√180= 0,66395.
Примем уровень значимости α = 0,05. В соответствии с правилом (параметрический критерий Колмогорова) проверяем, не превышает ли полученная статистика процентную точку распределения Колмогорова 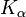 , при данном уровне значимости. , при данном уровне значимости.
Пользуемся таблицей 2.6. Как видно из этой таблицы λ < 1,3581. Таким образом, гипотеза о том, что закон распределения не противоречит статистическим данным, принимается на уровне значимости 0,05.
Таблица 2.6.
Процентные точки распределения статистики Колмогорова при проверке простой гипотезы
[1]
| Функция распределения |
Верхние процентные точки |
| 0,15 |
0,1 |
0,05
|
0,025 |
0,01 |
| K(S)
|
1,1379 |
1,2238 |
1,3581
|
1,4802 |
1,6276 |
2.3.1.
Проверка по критерию Пирсона гипотезы о том, что закон
распределения не противоречит статистическим данным.
Критерий согласия Пирсона хи-квадрат (χ2
) представляет собой сумму квадратов отклонений опытных и теоретических частот в каждом интервале статистического ряда информации и определяется по формуле:
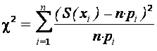 , ,
где S
(
xi
)
– эмпирическая частота в i-том интервале, n
∙
pi
- теоретическая частота в i-том интервале; n
= 180
, pi
=
F
(
xi
н
) -
F
(
xi
в
)
– разность значений функции распределения в начале i‑того интервала, и значения функции распределения в конце i‑того интервала.
Для расчетов в Excelcначала в ячейку S12 введем встроенную функцию ВЕЙБУЛЛ(). Аргументом Х возьмем нижнюю границу интервала, в качестве аргументов параметров функции распределения выберем найденные ранее значения из ЛИСТА2:
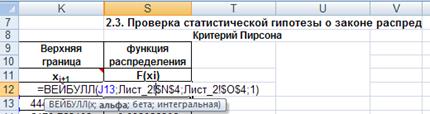
Рис. 38а. Ввод функции ВЕЙБУЛЛ().
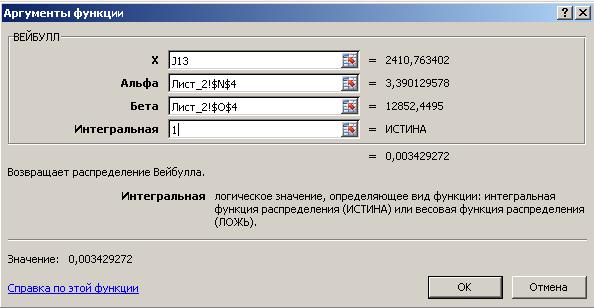
Рис. 38б. Ввод аргументов функции ВЕЙБУЛЛ().
Распространим формулу на остальные интервалы автозаполнением. В следующем столбце, в ячейку S13 введём формулу для расчета разности значений функции распределения в начале и конце интервала (рис.39). И распространим её на все интервалы.
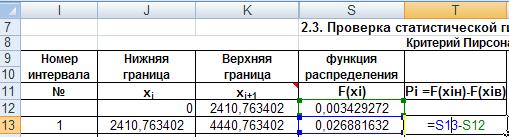
Рис. 39. Ввод формулы разности значений функции распределения в начале и конце интервала.
В следующем столбце рассчитываем теоретические частоты n*pi, для чего введем в ячейку U13 формулу=ОКРУГЛ(T13*180;0).
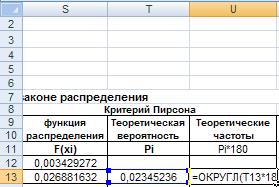
Рис. 40. Ввод формулы для расчета теоретической частоты.
Распространим формулу на другие интервалы. Так как на первом и последнем интервалах получили теоретические частоты ниже пяти, т.е. по 4, надо объединить 1-й и 2-й, 8-й и 9-й интервалы. Те же интервалы объединим в столбце эмпирических частот. Получим укрупненный статистический ряд с числом интервалов 7.
Введем в ячейку Х14 формулу =(W14-V14)^2/V14:
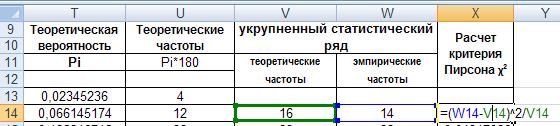
Рис. 41. Ввод формулы.
Распространим формулу на все интервалы. Далее в ячейке Х22 просуммируем полученные результаты столбца, получим значение критерия Пирсона.

Рис. 42. Ввод функции СУММ().
Получили значение критерия согласия Пирсона, равное 6,866. Далее для определения вероятности принятия гипотезы о распределении Вейбулла воспользуемся функцией Х2ОБР(). Для ввода функции нужно найти число степеней свободы (R). Число степеней свободы определяется по формуле:
R = k – z,
где k = 7 – число интервалов укрупнённого статистического ряда;
z – число обязательных связей. Для закона распределения Вейбулла число обязательных связей равно трем: две связи – 2 параметра распределения, третья связь – условие Sр = 1,0. Таким образом, R = 4.
Выбираем уровень значимости 0,05. И в ячейку Х23 вводим функцию Х2ОБР() с аргументами: Вероятность 0,05, Степень свободы 4.
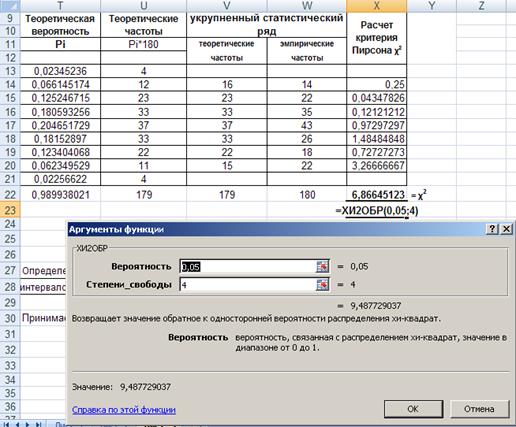
Рис. 43. Ввод функции Х2ОБР().
Получено значение χ2
кр
= 9,487. Результаты расчета и укрупненный статистический ряд показаны в таблице 2.7.
Таблица 2.7. Укрупненный статистический ряд.
| укрупненный статистический ряд
|
Расчет критерия Пирсона χ2
|
| теоретические частоты
|
эмпирические частоты
|
| 16 |
14 |
0,25 |
| 23 |
22 |
0,04347826 |
| 33 |
35 |
0,12121212 |
| 37 |
43 |
0,97297297 |
| 33 |
26 |
1,48484848 |
| 22 |
18 |
0,72727273 |
| 15 |
22 |
3,26666667 |
| 179 |
180 |
6,86645123
|
= χ2
|
| 9,48772904
|
= χкр2
|
Сравнение вычисленного значения 6,866 и найденного функцией – 9,487 показывает, что вычисленное значение ниже критического. Это позволяет сделать вывод о том, что распределение отказов в анализируемой выборки наработки между отказами с уровнем значимости 0,05 соответствует закону Вейбулла.
3. Анализ полученных результатов. Выводы.
Распределение наработок между отказами контактной сети переменного тока межподстанционной зоны может быть представлено законом Вейбулла с параметром формы b = 3.39 и параметром масштаба - а = 12852 при доверительной вероятности g = 0,95.
Среднее время безотказной работы – среднее значение наработки до первого отказа контактной сети с доверительной вероятностью 0,95 лежит в пределах 11571 <m(x) <11605 часов.
Литература
.
Прикладная математическая статистика. Кобзарь А.И_2006 -816с.
[1]
Таблицы предельных распределений статистик непараметрических критериев согласия при проверке простых и сложных гипотезhttp://fpmi.ami.nstu.ru/~headrd/seminar/nonparametric/table_B2.htm
|