ЗАДАНИЕ
Известны следующие данные о доходности капитала компании, уровне дивидендов и ценах акции:
| № |
Уровень дивидендов, % |
Доходность капитала, % |
Цена акции, д.е./шт. |
| 1 |
2,1 |
20,4 |
31 |
| 2 |
4,2 |
27,3 |
40 |
| 3 |
3,2 |
32,6 |
30 |
| 4 |
6,2 |
25,6 |
68 |
| 5 |
5,0 |
15,8 |
43 |
| 6 |
6,8 |
29,2 |
66 |
| 7 |
5,8 |
30,8 |
56 |
| 8 |
6,6 |
24,6 |
40 |
| 9 |
4,8 |
26,7 |
46 |
| 10 |
4,8 |
25,4 |
48 |
| 11 |
5,2 |
30,6 |
51 |
| 12 |
5,6 |
30,4 |
53 |
| 13 |
5,4 |
24,0 |
52 |
| 14 |
3,8 |
30,6 |
40 |
| 15 |
3,8 |
27,8 |
40 |
| 16 |
7,2 |
46,6 |
56 |
| 17 |
4,9 |
31,2 |
43 |
| 18 |
6,0 |
30,0 |
42 |
| 19 |
6,2 |
22,4 |
52 |
| 20 |
4,3 |
24,5 |
25 |
Требуется:
1. Построить линейное уравнение множественной регрессии и пояснить экономический смысл его параметров.
2. Рассчитать частные коэффициенты эластичности.
3. Определить стандартизованные коэффициенты регрессии.
4. сделать вывод о силе связи результативного показателя с каждым из факторов.
5. Определить парные и частные коэффициенты корреляции, а также множественный коэффициент корреляции.
6. Построить поля корреляции результативного показателя и факторов.
По результатам анализа пунктов 1. – 5, выбрать более значимый фактор и для него:
1. Определить параметры а и b уравнения парной линейной регрессии:
2. Линейный коэффициент корреляции.
3. Найти индекс корреляции.
4. На основании полученных двух моделей найти два значения результативного показателя при ожидаемых в среднем значениях х1
= 7%, х2
= 32,0%.
7. Сделать выводы.
Задание 1. Построить линейное уравнение множественной регрессии и пояснить экономический смысл его параметров
Модель множественной линейной регрессии:
y=a+b1*x1+b2*x2
Коэффициенты уравнения регрессии находятся из системы по МНК:
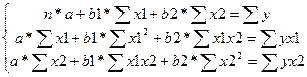
Расчетная таблица
| № |
Уровень дивидендов, %, х1 |
Доходность капитала, %, х2 |
Цена акции, д.е./шт., у |
х1*х1
|
х2*х2
|
у*у
|
х1*у
|
х2*у
|
х1*х2
|
| 1 |
2,1 |
20,4 |
31 |
4,41 |
416,16 |
961 |
65,1 |
632,4 |
42,84 |
| 2 |
4,2 |
27,3 |
40 |
17,64 |
745,29 |
1600 |
168 |
1092 |
114,66 |
| 3 |
3,2 |
32,6 |
30 |
10,24 |
1062,76 |
900 |
96 |
978 |
104,32 |
| 4 |
6,2 |
25,6 |
68 |
38,44 |
655,36 |
4624 |
421,6 |
1740,8 |
158,72 |
| 5 |
5 |
15,8 |
43 |
25 |
249,64 |
1849 |
215 |
679,4 |
79 |
| 6 |
6,8 |
29,2 |
66 |
46,24 |
852,64 |
4356 |
448,8 |
1927,2 |
198,56 |
| 7 |
5,8 |
30,8 |
56 |
33,64 |
948,64 |
3136 |
324,8 |
1724,8 |
178,64 |
| 8 |
6,6 |
24,6 |
40 |
43,56 |
605,16 |
1600 |
264 |
984 |
162,36 |
| 9 |
4,8 |
26,7 |
46 |
23,04 |
712,89 |
2116 |
220,8 |
1228,2 |
128,16 |
| 10 |
4,8 |
25,4 |
48 |
23,04 |
645,16 |
2304 |
230,4 |
1219,2 |
121,92 |
| 11 |
5,2 |
30,6 |
51 |
27,04 |
936,36 |
2601 |
265,2 |
1560,6 |
159,12 |
| 12 |
5,6 |
30,4 |
53 |
31,36 |
924,16 |
2809 |
296,8 |
1611,2 |
170,24 |
| 13 |
5,4 |
24 |
52 |
29,16 |
576 |
2704 |
280,8 |
1248 |
129,6 |
| 14 |
3,8 |
30,6 |
40 |
14,44 |
936,36 |
1600 |
152 |
1224 |
116,28 |
| 15 |
3,8 |
27,8 |
40 |
14,44 |
772,84 |
1600 |
152 |
1112 |
105,64 |
| 16 |
7,2 |
46,6 |
56 |
51,84 |
2171,56 |
3136 |
403,2 |
2609,6 |
335,52 |
| 17 |
4,9 |
31,2 |
43 |
24,01 |
973,44 |
1849 |
210,7 |
1341,6 |
152,88 |
| 18 |
6 |
30 |
42 |
36 |
900 |
1764 |
252 |
1260 |
180 |
| 19 |
6,2 |
22,4 |
52 |
38,44 |
501,76 |
2704 |
322,4 |
1164,8 |
138,88 |
| 20 |
4,3 |
24,5 |
25 |
18,49 |
600,25 |
625 |
107,5 |
612,5 |
105,35 |
| Итого
|
101,9
|
556,5
|
922
|
550,47
|
16186,4
|
44838
|
4897,1
|
25950,3
|
2882,69
|
| Среднее
|
5,095
|
27,825
|
46,1
|
27,5235
|
809,322
|
2241,9
|
244,855
|
1297,52
|
144,135
|
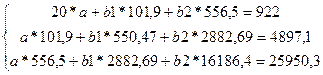
a=13,807
b1=6,391
b2=-0,01
y=13,807+6,391*х1-0,01*x2
При уровня дивидендов на 1 % цена 1 акции увеличивается на 6,391 д.е. При увеличении доходности капитала на 1 % цена 1 акции уменьшается на 0,01 д.е.
Задание 2. Рассчитать частные коэффициенты эластичности
Э(х1)=b1 * 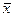 / / =6,391*5,095/46,1=0.706 =6,391*5,095/46,1=0.706
Э(х2)=b2 * 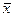 / /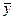 =-0,01*27,825/46,1=-0,006 =-0,01*27,825/46,1=-0,006
Задание 3. Определите стандартизованные коэффициенты регрессии
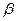 = b* = b*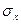 / /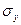
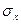 - стандартное отклонение факторного признака (х); - стандартное отклонение факторного признака (х);
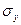 - стандартное отклонение результативного признака (у). - стандартное отклонение результативного признака (у).
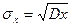 , , 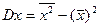
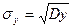 , , 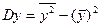
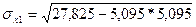 =1.251 =1.251
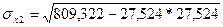 =7,194 =7,194
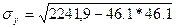 =10,802 =10,802
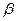 (х1)= b1* (х1)= b1*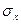 / /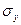 =6,391*1,251/10,802=0.74 =6,391*1,251/10,802=0.74
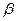 (х2)= b2* (х2)= b2*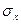 / /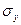 =-0,01*7,194/10,802=-0,007 =-0,01*7,194/10,802=-0,007
Задание 4. Сделайте вывод о силе связи результативного показателя с каждым из факторов
При неизменной доходности капитала при увеличении уровня дивидендов на 1 процентный пункт (п. п.) ее среднего значения цена акции увеличивается на 0,706 % ее среднего значения; при увеличении уровня дивидендов на 1 сигму цена акции увеличивается на 0,74 сигм.
При неизменном уровне дивидендов при увеличении доходности капитала на 1 п. п. его среднего значения цена акции уменьшается на 0,006 % ее среднего значения; при увеличении доходности капитала на 1 сигму цена акции уменьшается на 0,007 сигм.
Реклама

Задание 5. Определите парные и частные коэффициенты корреляции, а также множественный коэффициент корреляции
Парные коэффициенты корреляции:
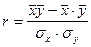
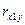 =(244,855-5,095*46,1)/(1,251*10,802) = 0,738 =(244,855-5,095*46,1)/(1,251*10,802) = 0,738
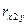 =(1297,52-27,825*46,1)/(7,194*10,802)= 0,19 =(1297,52-27,825*46,1)/(7,194*10,802)= 0,19
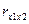 =(144,135-5,095*27,825)/(1,251*7,194)=0,263 =(144,135-5,095*27,825)/(1,251*7,194)=0,263
Частные коэффициенты корреляции:
- чистое влияние на цену акции фактора х1 – уровень дивидендов)
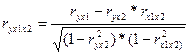
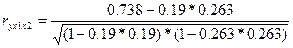 =0.726 =0.726
-чистое влияние на цену акции фактора х2 – доходности капитала
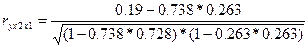 =-0,006 =-0,006
Коэффициент множественной корреляции:
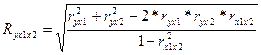
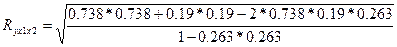 = 0.738 = 0.738
Задание 6. Построить поля корреляции результативного показателя и факторов
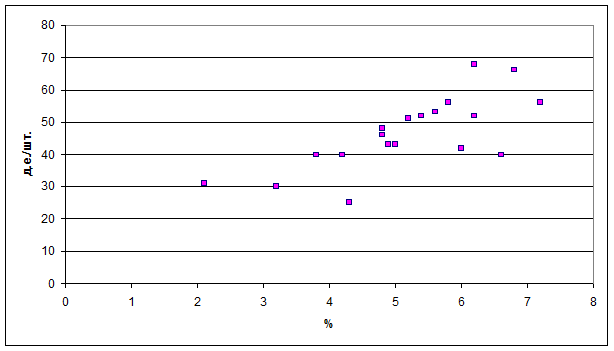
Поле корреляции фактора х1 (уровень дивидендов) и цены акции
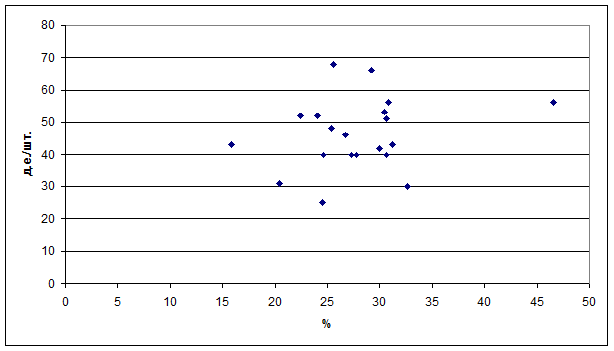
Поле корреляции фактора х2 (доходность капитала) и цены акции
По результатам анализа п. 1-5 выбрать наиболее значимый фактор и для него:
1)
определить параметры
a
и
b
уравнения парной регрессии
Наиболее значимый фактор х1 ( уровень дивидендов)
Линейная функция: yх3
=a + b*х1. Параметры а и b определяются по способу наименьшим квадратов путем решением следующей системы нормальных уравнений:
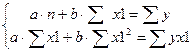 , ,
Расчетная таблица
| №
|
Уровень дивидендов, %, х1
|
Цена акции, д.е./шт., у
|
х1*х1
|
у*у
|
х1*у
|
у(х) |
(у(х)-у)^2 |
(y-cp y)^2 |
| 1 |
2,1 |
31 |
4,41 |
961 |
65,1 |
27,0026 |
15,9792 |
228,01 |
| 2 |
4,2 |
40 |
17,64 |
1600 |
168 |
40,3922 |
0,15382 |
37,21 |
| 3 |
3,2 |
30 |
10,24 |
900 |
96 |
34,0162 |
16,1299 |
259,21 |
| 4 |
6,2 |
68 |
38,44 |
4624 |
421,6 |
53,1442 |
220,695 |
479,61 |
| 5 |
5 |
43 |
25 |
1849 |
215 |
45,493 |
6,21505 |
9,61 |
| 6 |
6,8 |
66 |
46,24 |
4356 |
448,8 |
56,9698 |
81,5445 |
396,01 |
| 7 |
5,8 |
56 |
33,64 |
3136 |
324,8 |
50,5938 |
29,227 |
98,01 |
| 8 |
6,6 |
40 |
43,56 |
1600 |
264 |
55,6946 |
246,32 |
37,21 |
| 9 |
4,8 |
46 |
23,04 |
2116 |
220,8 |
44,2178 |
3,17624 |
0,01 |
| 10 |
4,8 |
48 |
23,04 |
2304 |
230,4 |
44,2178 |
14,305 |
3,61 |
| 11 |
5,2 |
51 |
27,04 |
2601 |
265,2 |
46,7682 |
17,9081 |
24,01 |
| 12 |
5,6 |
53 |
31,36 |
2809 |
296,8 |
49,3186 |
13,5527 |
47,61 |
| 13 |
5,4 |
52 |
29,16 |
2704 |
280,8 |
48,0434 |
15,6547 |
34,81 |
| 14 |
3,8 |
40 |
14,44 |
1600 |
152 |
37,8418 |
4,65783 |
37,21 |
| 15 |
3,8 |
40 |
14,44 |
1600 |
152 |
37,8418 |
4,65783 |
37,21 |
| 16 |
7,2 |
56 |
51,84 |
3136 |
403,2 |
59,5202 |
12,3918 |
98,01 |
| 17 |
4,9 |
43 |
24,01 |
1849 |
210,7 |
44,8554 |
3,44251 |
9,61 |
| 18 |
6 |
42 |
36 |
1764 |
252 |
51,869 |
97,3972 |
16,81 |
| 19 |
6,2 |
52 |
38,44 |
2704 |
322,4 |
53,1442 |
1,30919 |
34,81 |
| 20 |
4,3 |
25 |
18,49 |
625 |
107,5 |
41,0298 |
256,954 |
445,21 |
| Итого
|
101,9
|
922
|
550,47
|
44838
|
4897,1
|
921,974
|
1061,67
|
2333,8
|
| Среднее
|
5,095
|
46,1
|
27,5235
|
2241,9
|
244,855
|
-
|
-
|
-
|
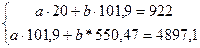
а=13,613
b=6,376
y(x1)=13,613+6,376*x1
2)
линейный коэффициент корреляции
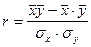
 =(244,855-5,095*46,1)/(1,251*10,802) = 0,738 =(244,855-5,095*46,1)/(1,251*10,802) = 0,738
3)
найти индекс корреляции
Индекс корреляции:
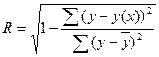
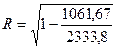 =0,738 =0,738
4)
на основании полученных двух моделей найти два значения результативного показателя при ожидаемых в среднем значениях х1=7%, х2=32%.
Y(х1, х2)=13,807+6,391*х1-0,01*x2
y(7;32)= 13,807+6,391*7-0,01*32 = 58,224 д.е. за штуку
y(x1)=13,613+6,376*x1
y(7)=13,613+6,376*7=58,245 д.е. за штуку
7. Сделать выводы
Цена акции зависит от уровня дивидендов и доходности капитала. Как показали расчеты связь между уровнем дивидендов и ценой акции умеренно-сильная, прямая. Связь между доходностью капитала и ценой акции слабая обратная. Совместное влияние двух факторов может быть оценено как достаточно сильное.
При ожидаемых в среднем значениях уровня дивидендов (7%) и доходности капитала (32%) цена акции будет находится в интервале от 52,22 до 52,25 д.е. за штуку.
|