Теоретический вопрос: Организация выборочных наблюдений и обеспечение репрезентативности выборки
Выборочное статистическое наблюдение является наиболее широко применяемым видом не сплошного наблюдения. При выборочном методе обследованию подвергается сравнительно набольшая часть всей изучаемой совокупности (обычно до 5-10 %, реже до 15-20 %). При этом подлежащая изучению статистическая совокупность, из которой производится отбор части единиц, называется генеральной совокупностью. Отобранная из генеральной совокупности некоторая часть единиц, подвергающаяся обследованию, называется выборочной совокупностью или выборкой. Значение выборочного метода состоит в том, что при минимальной численности обследуемых единиц проведение исследования осуществляется в более короткие сроки и с минимальными затратами труда и средств. Это повышает оперативность статистической информации, уменьшает ошибки регистрации.
Под выборочным понимается метод статистического исследования, при котором обобщающие показатели изучаемой совокупности устанавливаются по некоторой ее части, организованной по принципу случайного отбора.
При случайном отборе каждой единице изучаемого объекта (массового явления, генеральной совокупности) обеспечивается определенная (обычно равная) вероятность попасть в количество обследуемых единиц (в выборку) и тем самым исключается субъективность, тенденциозность и односторонность в подборе этих единиц.
При строгом соблюдении принятых правил отбора выборочное наблюдение репрезентативно в широком смысле слова: при нем обеспечивается близкое соответствие состава охваченной наблюдением выборки и состава генеральной совокупности. Благодаря этому по данных выборочного наблюдения можно определить с желательной степенью приближения интересующие исследователей характеристики изучаемого явления.
Выборочный метод при проведении ряда исследований является единственно возможным, например, при контроле качества продукции (товара).
Выборочный метод иногда применяется для проверки данных даже сплошного учета. Минимальная численность обследуемых единиц позволяет провести исследование более тщательно и квалифицированно. Так, при переписи населения практикуются выборочные контрольные обходы для проверки правильности записей сплошного наблюдения.
Реклама

Проведение выборочного наблюдения складывается из ряда последовательных этапов:
1) обоснование целесообразности проведения выборочного метода в соответствии с задачами исследования;
2) составление программы проведения статистического исследования выборочным методом;
3) решение организационных вопросов сбора исходной информации;
4) установление доли выборки, т.е. части подлежащих обследованию единиц генеральной совокупности;
5) обоснование способов формирования выборочной совокупности;
6) осуществление отбора единиц из генеральной совокупности для их обследования;
7) фиксация в отобранных единицах выборки значений изучаемых признаков;
статистическая обработка полученной в выборке информации с определением обобщающих характеристик изучаемых признаков;
9) определение количественной оценки ошибки выборки;
10) распространение обобщающих выборочных характеристик на генеральную совокупность.
В зависимости от способа организации выборочного наблюдения и применяемых способов отбора различают также виды выборочного наблюдения:
1) простая случайная выборка (собственно-случайная);
2) механическая случайная выборка;
3) типическая случайная выборка;
4) серийная (гнездовая) выборка;
5) многоступенчатая (многостепенная или комбинационная) выборка.
Выборку можно производить из конечной (ограниченной) и неограниченной генеральной совокупности. Поэтому целесообразно различать выборочный метод и по этому признаку. Иногда различают также большие, охватывающие значительное число обследуемых единиц, выборки и малые выборки.
Каждый из указанных основных способов отбора может реализоваться по схеме повторного (когда зафиксированная в выборке единица возвращается в генеральную совокупность) или бесповоротного отбора (когда зафиксированная единица исключается из дальнейшего просмотра и может попасть в выборку только один раз). Целесообразно различать выборки и по этому признаку.
Большую актуальность приобретает выборочный метод в условиях перехода к рыночной экономике. Развитие различных форм собственности, изменения в характере экономических отношений, как указывалось в предыдущих лекциях, обусловливают изменения функций учета и статистики, сокращение и упрощение статистической отчетности.
По сравнению с другими методами, применяющими не сплошное наблюдение, выборочный метод имеет существенное преимущество. При соблюдении правил научной организации выборочного наблюдения появляется возможность количественной оценки ошибки репрезентативности (представительности).
Реклама

Репрезентативность означает, что с некоторой наперед заданной или определенной статистически погрешностью можно считать, что представленное в выборочной совокупности распределение изучаемых признаков соответствует их реальному распределению. Для обеспечения репрезентативности выборки данных необходимо учесть ряд обязательных для любого исследования условий. Среди них важнейшими являются следующие:
- каждая единица генеральной совокупности должна иметь равную вероятность попадания в выборку
- выборка переменных производится независимо от изучаемого признака
- отбор производится из однородных совокупностей
- число единиц в выборке должно быть достаточно большим
- выборка и генеральная совокупность должны быть по возможности статистически однородны.
Задача 1
Вычислить индексы сезонности и построить сезонную волну за полугодие.
| год |
| 1 |
2 |
3 |
| январь |
26,2 |
27,5 |
27,2 |
| февраль |
25,8 |
27,1 |
26,8 |
| март |
25,6 |
26,9 |
26,5 |
| апрель |
25,4 |
26,6 |
26,3 |
| май |
26,5 |
27,9 |
27,5 |
| июнь |
26,8 |
28,2 |
27,8 |
Решение
Решение сведем в таблицу:
| год |
Всего за три года |
В среднем за три года |
Индекс сезонности |
| 1 |
2 |
3 |
| 1 |
2 |
3 |
4 |
5=2+3+4 |
6=5/3 |
7 |
| январь |
26,2 |
27,5 |
27,2 |
80,9 |
26,97 |
16,56% |
| февраль |
25,8 |
27,1 |
26,8 |
79,7 |
26,57 |
16,31% |
| март |
25,6 |
26,9 |
26,5 |
79 |
26,33 |
16,17% |
| апрель |
25,4 |
26,6 |
26,3 |
78,3 |
26,10 |
16,03% |
| май |
26,5 |
27,9 |
27,5 |
81,9 |
27,30 |
16,76% |
| июнь |
26,8 |
28,2 |
27,8 |
82,8 |
27,60 |
16,95% |
| Итого |
157,3 |
166,2 |
165,1 |
488,6 |
162,87 |
Построим волну сезонности:

Вывод:
В динамике показателей явно прослеживается наличие сезонной компоненты. Наибольшим средним значением характеризуется месяц июнь (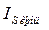 =16,95%), а наименьшее среднее значение приходится на апрель ( =16,95%), а наименьшее среднее значение приходится на апрель ( =16,03%). График сезонной волны наглядно демонстрирует наличие сезонной компоненты в изучаемом показателе. =16,03%). График сезонной волны наглядно демонстрирует наличие сезонной компоненты в изучаемом показателе.
Задача 2.
Имеются данные о 23 рабочих-сдельщиках, представленные в следующей таблице:
| Номер рабочих |
Стаж работы, лет |
Месячная выработка продукции, у.е. |
| 1 |
14 |
285 |
| 2 |
19,5 |
375 |
| 3 |
22,5 |
392 |
| 4 |
17,5 |
340 |
| 5 |
19 |
345 |
| 6 |
15,5 |
318 |
| 7 |
15,7 |
310 |
| 8 |
29 |
405 |
| 9 |
26,2 |
377 |
| 10 |
27 |
417 |
| 11 |
24 |
390 |
| 12 |
25 |
373 |
| 13 |
23,5 |
371 |
| 14 |
14 |
317 |
| 15 |
22 |
355 |
| 16 |
18 |
330 |
| 17 |
19 |
347 |
| 18 |
23,2 |
353 |
| 19 |
18 |
305 |
| 20 |
18,4 |
335 |
| 21 |
20,5 |
343 |
| 22 |
21,5 |
353 |
| 23 |
21 |
360 |
Для изучения зависимости между приведенными показателями произвести группировку рабочих по стажу работы, выделив 5 групп с равными интервалами. По каждой из них и в совокупности подсчитать количество рабочих (абсолютное и в процентах к итогу), средний стаж работы, среднемесячную выработку продукции. Результаты представить в таблице, сделать краткие выводы.
Решение
Определяем величину интервала: 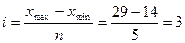
Разбиваем на группы: [14; 17), [17; 20), [20; 23), [23; 26), [26, 29].
Строим вспомогательную таблицу для рассчитанных интервалов:
| Размер интервала |
Номер рабочих |
Стаж работы, лет |
Месячная выработка продукции, у.е. |
| [14; 17) |
1 |
14 |
285 |
| 6 |
15,5 |
318 |
| 7 |
15,7 |
310 |
| 14 |
14 |
317 |
| Итого |
4 |
59,2 |
1230 |
| [17; 20) |
2 |
19,5 |
375 |
| 4 |
17,5 |
340 |
| 5 |
19 |
345 |
| 16 |
18 |
330 |
| 17 |
19 |
347 |
| 19 |
18 |
305 |
| 20 |
18,4 |
335 |
| Итого |
7 |
129,4 |
2377 |
| [20; 23) |
3 |
22,5 |
392 |
| 15 |
22 |
355 |
| 21 |
20,5 |
343 |
| 22 |
21,5 |
353 |
| 23 |
21 |
360 |
| Итого |
5 |
107,5 |
1803 |
| [23; 26) |
11 |
24 |
390 |
| 12 |
25 |
373 |
| 13 |
23,5 |
371 |
| 18 |
23,2 |
353 |
| Итого |
4 |
95,7 |
1487 |
| [26, 29] |
8 |
29 |
405 |
| 9 |
26,2 |
377 |
| 10 |
27 |
417 |
| Итого |
3 |
82,2 |
1199 |
Стоим итоговую таблицу:
Группировка рабочих по стажу работы за … год
| Группы рабочих по стажу работы, лет |
Число рабочих |
Стаж работы, лет |
Месячная выработка продукции, у.е. |
| абсолютное |
в % к итогу |
всего |
на 1 чел. |
всего |
на 1 чел |
| 1 |
2 |
3 |
4 |
5=4/2 |
6 |
7=6/2 |
| [14; 17) |
4,0 |
17,4 |
59,2 |
14,8 |
1230 |
307,5 |
| [17; 20) |
7,0 |
30,4 |
129,4 |
18,5 |
2377 |
339,6 |
| [20; 23) |
5,0 |
21,7 |
107,5 |
21,5 |
1803 |
360,6 |
| [23; 26) |
4,0 |
17,4 |
95,7 |
23,9 |
1487 |
371,8 |
| [26, 29] |
3,0 |
13,0 |
82,2 |
27,4 |
1199 |
399,7 |
| Итого: |
23,0 |
100,0 |
474,0 |
20,6 |
8096,0 |
352,0 |
Вывод: для всех групп рабочих характерна следующая тенденция: с увеличением стажа работы растет месячная выработка продукции 1 человеком. Также можно отметить тот факт, что больше всего рабочих имеют стаж от 7 до 10 лет, а затем количество рабочих с ростом стажа начинает снижаться.
Задача 3.
1. Построить прогноз методом среднего абсолютного прироста. Обосновать метод выбора прогнозирования, предварительно проверив предпосылки его реализации.
2. Построить прогноз методом среднего темпа роста, предварительно проверив предпосылки его реализации.
3. Построить прогноз методом экстраполяции трендовых моделей.
4. Произвести оценку точности прогнозов, полученных методом экстраполяции трендовых моделей на основе:
- средней квадратической ошибки
- коэффициента несоответствия.
Сделать выводы.
Исходные данные:
Динамика числа семей, состоявших на учете на получение жилья в одном из регионов Республики Беларусь за январь-октябрь 2009 года
| Месяц |
Число семей, состоявших на учете на получение жилья, тыс.ед., yi
|
| Январь |
175,60 |
| Февраль |
177,20 |
| Март |
199,30 |
| Апрель |
202,10 |
| Май |
222,90 |
| Июнь |
244,00 |
| Июль |
257,30 |
| Август |
227,90 |
| Сентябрь |
251,10 |
| Октябрь |
295,00 |
Решение
Прогноз методом среднего абсолютного прироста
| Месяц |
Число семей, состоявших на учете на получение жилья, тыс.ед., yi
|
yi
2
|
∆i
|
∆i
2
|
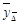
|
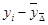
|
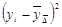
|
| Январь |
175,60 |
30835,36 |
- |
- |
175,600 |
0,000 |
0,000 |
| Февраль |
177,20 |
31399,84 |
1,60 |
2,56 |
188,867 |
-11,667 |
136,111 |
| Март |
199,30 |
39720,49 |
22,10 |
488,41 |
202,133 |
-2,833 |
8,028 |
| Апрель |
202,10 |
40844,41 |
2,80 |
7,84 |
215,400 |
-13,300 |
176,890 |
| Май |
222,90 |
49684,41 |
20,80 |
432,64 |
228,667 |
-5,767 |
33,254 |
| Июнь |
244,00 |
59536,00 |
21,10 |
445,21 |
241,933 |
2,067 |
4,271 |
| Июль |
257,30 |
66203,29 |
13,30 |
176,89 |
255,200 |
2,100 |
4,410 |
| Август |
227,90 |
51938,41 |
-29,40 |
864,36 |
268,467 |
-40,567 |
1645,654 |
| Сентябрь |
251,10 |
63051,21 |
23,20 |
538,24 |
281,733 |
-30,633 |
938,401 |
| Октябрь |
295,00 |
87025,00 |
43,90 |
1927,21 |
295,000 |
0,000 |
0,000 |
| Итого |
2252,40 |
520238,42 |
119,40 |
4883,36 |
2353,000 |
-100,600 |
2947,020 |
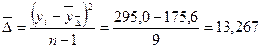
Для осуществления прогноза должна выполняться предпосылка:
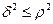
Проверим:
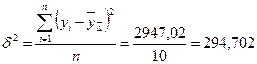
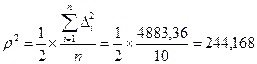
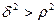
Условие не выполняется, следовательно, прогноз построить нельзя.
Прогноз методом среднего темпа роста
| Месяц |
Число семей, состоявших на учете на получение жилья, тыс.ед., yi
|
Тр |
уТр
|
| Январь |
175,60 |
- |
175,60 |
| Февраль |
177,20 |
1,009 |
186,022 |
| Март |
199,30 |
1,125 |
197,062 |
| Апрель |
202,10 |
1,014 |
208,758 |
| Май |
222,90 |
1,103 |
221,148 |
| Июнь |
244,00 |
1,095 |
234,273 |
| Июль |
257,30 |
1,055 |
248,177 |
| Август |
227,90 |
0,886 |
262,906 |
| Сентябрь |
251,10 |
1,102 |
278,510 |
| Октябрь |
295,00 |
1,175 |
295,039 |
| Итого |
2252,40 |
9,56 |
2307,49 |
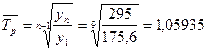
Проверим предпосылки осуществления прогноза:
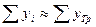
2252,40 < 2307,49
Так как предпосылки не выполняются, прогноз методом среднего темпа роста построить невозможно.
Прогноз методом экстраполяции трендовых моделей.
Модель прямой.
| Месяц |
Число семей, состоявших на учете на получение жилья, тыс.ед., yi
|
Номер месяца, t |
t2
|
yi
xt |
yt
|
(yi
-yt
)2
|
yi
2
|
| Январь |
175,6 |
1 |
1 |
175,6 |
172,8327 |
7,657798 |
30835,36 |
| Февраль |
177,2 |
2 |
4 |
354,4 |
184,4788 |
52,98075 |
31399,84 |
| Март |
199,3 |
3 |
9 |
597,9 |
196,1248 |
10,08159 |
39720,49 |
| Апрель |
202,1 |
4 |
16 |
808,4 |
207,7709 |
32,15921 |
40844,41 |
| Май |
222,9 |
5 |
25 |
1114,5 |
219,417 |
12,1315 |
49684,41 |
| Июнь |
244 |
6 |
36 |
1464 |
231,063 |
167,3652 |
59536 |
| Июль |
257,3 |
7 |
49 |
1801,1 |
242,7091 |
212,8946 |
66203,29 |
| Август |
227,9 |
8 |
64 |
1823,2 |
254,3552 |
699,875 |
51938,41 |
| Сентябрь |
251,1 |
9 |
81 |
2259,9 |
266,0012 |
222,0461 |
63051,21 |
| Октябрь |
295 |
10 |
100 |
2950 |
277,6473 |
301,1171 |
87025 |
| Итого |
2252,4 |
55 |
385 |
13349 |
2252,4 |
1718,309 |
520238,42 |
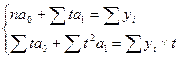
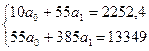

Yt = 161,57+11,65t
Построим прогноз:
| Номер месяца, t |
yt
|
| 11 |
289,2933 |
| 12 |
300,9394 |
| 13 |
312,5855 |
Оценка точности прогноза:
Среднеквадратическая ошибка:
 13,11 13,11
Коффициент несоответствия:
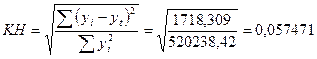
Модель параболы
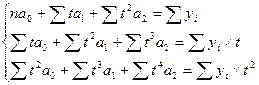


Yt = 161,7867 + 11,34606t + 0,027273t2
Построим прогноз:
| Номер месяца, t |
yt
|
| 11 |
289,8933 |
| 12 |
301,8667 |
| 13 |
313,8945 |
| Месяц |
Число семей, состоявших на учете на получение жилья, тыс.ед., yi
|
Номер месяца, t |
t2
|
t3
|
t4
|
yi
xt |
yi
xt2
|
yt
|
(yi
-yt
)2
|
yi
2
|
| Январь |
175,6 |
1 |
1 |
1 |
1 |
175,6 |
175,6 |
173,16 |
5,9536 |
30835,36 |
| Февраль |
177,2 |
2 |
4 |
8 |
16 |
354,4 |
708,8 |
184,5879 |
54,58075 |
31399,84 |
| Март |
199,3 |
3 |
9 |
27 |
81 |
597,9 |
1793,7 |
196,0703 |
10,43094 |
39720,49 |
| Апрель |
202,1 |
4 |
16 |
64 |
256 |
808,4 |
3233,6 |
207,6073 |
30,33005 |
40844,41 |
| Май |
222,9 |
5 |
25 |
125 |
625 |
1114,5 |
5572,5 |
219,1988 |
13,69897 |
49684,41 |
| Июнь |
244 |
6 |
36 |
216 |
1296 |
1464 |
8784 |
230,8448 |
173,058 |
59536 |
| Июль |
257,3 |
7 |
49 |
343 |
2401 |
1801,1 |
12607,7 |
242,5455 |
217,6966 |
66203,29 |
| Август |
227,9 |
8 |
64 |
512 |
4096 |
1823,2 |
14585,6 |
254,3006 |
696,992 |
51938,41 |
| Сентябрь |
251,1 |
9 |
81 |
729 |
6561 |
2259,9 |
20339,1 |
266,1103 |
225,3092 |
63051,21 |
| Октябрь |
295 |
10 |
100 |
1000 |
10000 |
2950 |
29500 |
277,9745 |
289,8661 |
87025 |
| Итого |
2252,4 |
55 |
385 |
3025 |
25333 |
13349 |
97300,6 |
2252,4 |
1717,916 |
520238,4 |
Оценка точности прогноза:
Среднеквадратическая ошибка:
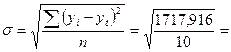 13,10693 13,10693
Коффициент несоответствия:
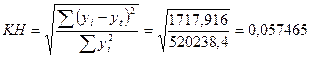
Выводы:
Таккак коэффициенты несоответствия при построении модели прямой и модели параболы близки к нулю, можно сказать, что прогноз будет довольно точен. Однако значение среднеквадратического отклонения (не близкое к нулю) и в первом, и во втором случае указывает на то, что прогноз не будет совершенным. Исходя из того, что значения показателей оценки точности прогноза в случае построения модели параболы ниже, чем при построении модели прямой, для расчета прогнозируемых значений следует воспользоваться моделью параболы. Получаем, что в ноябре 2009 года число семей, состоящих на учете на получение жилья, составит 289,9 тыс., в декабре – 301,87 тыс., в январе 2010 года – 313,89 тыс.
|