СТАТИСТИКА
Контрольная работа
Задание 1
По данным таблицы 1.1, путем прибавления к исходным данным трехзначной цифры, соответствующей трем последним цифрам зачетной книжки (308), рассчитать уровни каждого ряда.
Таблица 1.1
Исходные данные
| Месяц
|
Выпуск продукции, тыс.руб.
|
Численность рабочих (на конец месяца), чел.
|
Фонд заработной платы, тыс.руб.
|
| Январь |
678308 |
11268 |
225308 |
| Февраль |
679208 |
11408 |
237508 |
| Март |
679308 |
11408 |
237308 |
| Апрель |
679508 |
11908 |
238308 |
| Май |
679908 |
11958 |
240508 |
| Июнь |
679408 |
11908 |
240308 |
| Июль |
685608 |
12128 |
241708 |
| Август |
686208 |
12308 |
243808 |
| Сентябрь |
685508 |
12208 |
242308 |
| Октябрь |
686408 |
12808 |
244608 |
| Ноябрь |
684608 |
12828 |
246008 |
| Декабрь |
699508 |
13058 |
246608 |
средний уровень ряда 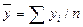 |
683624,6667 |
12099,66667 |
240358 |
| сумма ряда |
8203496 |
145196 |
2884296 |
Задание 2
Методом укрупнения интервалов исходные данные привести к квартальным
уровням и составить таблицу 2.1. Проанализировать тенденцию.
Таблица 2.1
Квартальные уровни
| Квартал
|
Первый
|
Второй
|
Третий
|
Четвертый
|
| Выпуск продукции,тыс.руб. |
2036824
|
2038824
|
2057324
|
2070524
|
| Численность, чел. |
34084
|
35774
|
36644
|
38694
|
| Фонд заработной платы, тыс.руб. |
700124
|
719124
|
727824
|
737224 |
Таким образом, одну и ту же тенденцию: рост величины показателя с течением времени.
Задание 3
По данным таблицы 2.1 определить все виды возможных относительных величин. Составить соответствующие таблицы. Проанализировать тенденцию их изменения.

Все уровни имеют одинаковый удельный вес в структуре выпуска. Наибольший базисный коэффициент роста наблюдается в 4 квартале, а цепной в третьем квартале. Наибольшие темпы роста и темпы прироста дают базисные показатели, причем наибольшее увеличении этих темпов происходит к 4 кварталу, тогда как в цепных после 3 квартала величина показателей темпов роста снижается.

Наибольший дельный вес в общей структуре имеет показатель 4 квартала 0,26,а наименьший в первом. Показатели темпов роста увеличиваются с течением времени в большей степени. Базисные стабильно растут с каждым кварталом, а вот цепные снижают темпы рост в 3 квартале, но уже к 4 вновь начинают расти.

Базисные показатели растут в меньшей степени, чем численность, но в большей степени чем выпуск

Задание 4
Рассчитать средние показатели для первого и второго ряда динамики.
| выпуск |
численность |
| Январь |
678308 |
11268 |
| Февраль |
679208 |
11408 |
| Март |
679308 |
11408 |
| Апрель |
679508 |
11908 |
| Май |
679908 |
11958 |
| Июнь |
679408 |
11908 |
| Июль |
685608 |
12128 |
| Август |
686208 |
12308 |
| Сентябрь |
685508 |
12208 |
| Октябрь |
686408 |
12808 |
| Ноябрь |
684608 |
12828 |
| Декабрь |
699508 |
13058 |
| общая средняя |
683624,6667 |
12099,66667 |
| средний абсолютный прирост |
1927,272727 |
162,7272727 |
| средний коэффициент роста |
1,002801421 |
1,013413104 |
| средний % темп роста |
100,2801421 |
101,3413104 |
| средний % темп прироста |
0,2801421 |
1,3413104 |
Задание 5
По показателю выпущенной продукции (данные таблицы 1.1) рассчитать и
проанализировать все показатели вариации.
| Хi |
линейное отклонение |
(Xi-Xsrednee)^2 |
| Январь |
678308 |
443,0555556 |
28266944,44 |
| Февраль |
679208 |
368,0555556 |
19506944,44 |
| Март |
679308 |
359,7222222 |
18633611,11 |
| Апрель |
679508 |
343,0555556 |
16946944,44 |
| Май |
679908 |
309,7222222 |
13813611,11 |
| Июнь |
679408 |
351,3888889 |
17780277,78 |
| Июль |
685608 |
165,2777778 |
3933611,111 |
| Август |
686208 |
215,2777778 |
6673611,111 |
| Сентябрь |
685508 |
156,9444444 |
3546944,444 |
| Октябрь |
686408 |
231,9444444 |
7746944,444 |
| Ноябрь |
684608 |
81,94444444 |
966944,4444 |
| Декабрь |
699508 |
1323,611111 |
252280277,8 |
| среднее линейное отклонение |
4350 |
| общая средняя |
683624,6667 |
| дисперсия |
32508055,56 |
| среднее квадратическое отклонение |
5701,583601 |
| коэффициент оссиляции,% |
3,10111689 |
| относительное линейное отклонение,% |
0,636314079 |
| коэффициент вариации,% |
0,83402251 |
Чем меньше дисперсия и среднее квадратическое отклонение, тем надежнее средняя величина, в нашем случае показатели достаточно велики, что говорит о несколько низкой надежности общей средней. По коэффициенту оссиляции можно сказать, что колеблемость крайних значений вокруг средней составляет примерно 3,1%. А по относительному линейному отклонению доля усредненного значения признака абсолютных отклонений от средней величины составляет 0,64%. Коэффициент вариации также имеет небольшую величину, что говорит о типичности общей средней, а совокупность можно в целом характеризовать как однородную.
Реклама

Задание 6
По показателю численности рабочих (данные таблицы 1.1) определить темпы
роста, абсолютные приросты, темпы прироста, абсолютную величину 1% прироста.
Вычислить также средние показатели динамики. Сделать выводы.
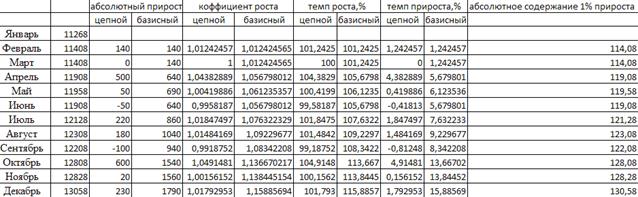
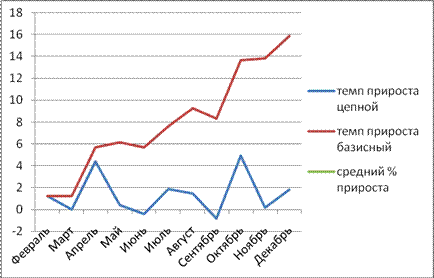
Абсолютные показатели не позволяют адекватно оценить данные. Если характеризовать совокупность по приросту, то мы видим, что существует вполне закономерная тенденция к росту, хотя в частности по месяцам показатели могут колебаться.
Задание 7
Изучить методы сглаживания рядов динамики скользящей средней и аналитического выравнивания. По показателю фонда заработной платы (данные таблицы 1.1) выполнить подробные вспомогательные и основные расчеты. Теоретически обосновать расчеты и полученные результаты.
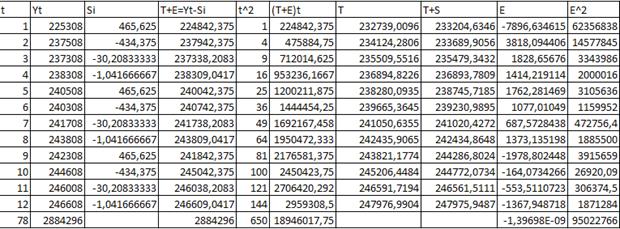
Метод аналитического выравнивания

С помощью МНК найдем оценка параметров уравнения.
Yteor=240358+1446,363636xi
Найдем расчетное значения F-критерия как отношение общей дисперсии к остаточной, получается 28,466. Табличное значении при уровне значимости 5 % составляет 4,96. Следовательно, наблюдаемое значение больше теоретического, тогда полученное уравнение значимо и оно адекватно отражает сложившуюся в исследуемом ряду динамики тенденцию.
Метод скользящей средней
| итого за квартал |
СС за квартал |
ЦСС |
оценка СК |
| 1 |
225308 |
| 2 |
237508 |
| 3 |
237308 |
938432 |
234608 |
236508 |
800 |
| 4 |
238308 |
953632 |
238408 |
238758 |
-450 |
| 5 |
240508 |
956432 |
239108 |
239658 |
850 |
| 6 |
240308 |
960832 |
240208 |
240895,5 |
-587,5 |
| 7 |
241708 |
966332 |
241583 |
241808 |
-100 |
| 8 |
243808 |
968132 |
242033 |
242570,5 |
1237,5 |
| 9 |
242308 |
972432 |
243108 |
243645,5 |
-1337,5 |
| 10 |
244608 |
976732 |
244183 |
244533 |
75 |
| 11 |
246008 |
979532 |
244883 |
| 12 |
246608 |
СС - скользящая средняя
ЦСС – центрированная скользящая средняя
СК – сезонная компонента
| номер кваратала |
| I |
II |
III |
IV |
| 1 |
800 |
-450 |
| 2 |
850 |
-587,5 |
-100 |
1237,5 |
| 3 |
1337,5 |
75 |
| итого за I квартал |
2187,5 |
-512,5 |
700 |
787,5 |
| средняя оценка |
729,1666667 |
-170,8333333 |
233,333333 |
262,5 |
| скорректированная оценка |
465,625 |
-434,375 |
-30,208333 |
-1,04166667 |
| к |
263,5416667 |
Методом Мнк найдем оценки параметров сглаживающего уравнения:
| d |
12 |
78 |
1716 |
| 78 |
650 |
| da |
2884296 |
78 |
397003015,5 |
| 18946018 |
650 |
| db |
12 |
2884296 |
2377125 |
| 78 |
18946017,75 |
| a |
231353,7 |
| b |
1385,271 |
Yteor=231353,7+1385,271xi
Задание 8
Индексным методом определить влияние на изменение фонда заработной платы в декабре по сравнению с январем средней заработной платы на одного рабочего и их численности.

В абсолютном изменении величина фонда выросла. Средний уровень заработной платы отрицательно влияет на абсолютное изменение фондов, а вот рост среднесписочной численности оказывает положительное влияние. Общее изменение по обоим показателям совпадает с абсолютным изменением фонда.
Задание 9
С помощью корреляционно-регрессионного анализа изучить связь между первым и вторым признаками. Для этого:
а) построить эмпирическую линию регрессии;
б) оценить тесноту связи между признаками;
в) найти уравнение связи, график которого представить в той же системе координат, что и эмпирическая линия регрессии.
г) сделать выводы.
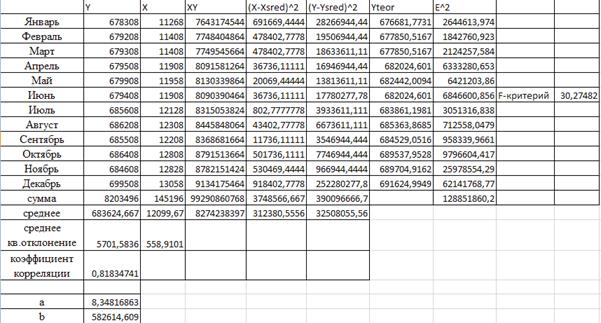
Судя по коэффициенту корреляции связь между признаками сильная, прямая, то есть с ростом численности растет величина выпускаемой продукции.
Yteor=8,34816863+582614,609xi
Табличное значения критерия Фишера при 5-ти процентном уровне значимости 4,75, что меньше наблюдаемого, следовательно, полученное уравнение значимо.
Реклама

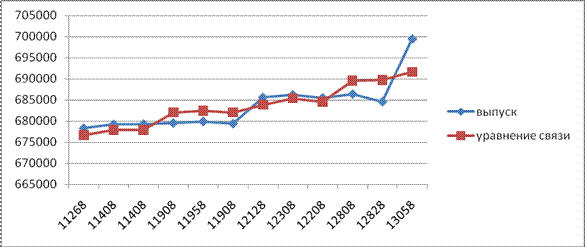
Задание 10
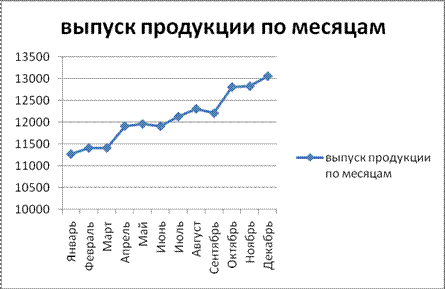
По показателю численности рабочих (данные таблицы 1.1) построить точечные и круговые диаграммы, полигоны, гистограммы, кумулятивные огивы.
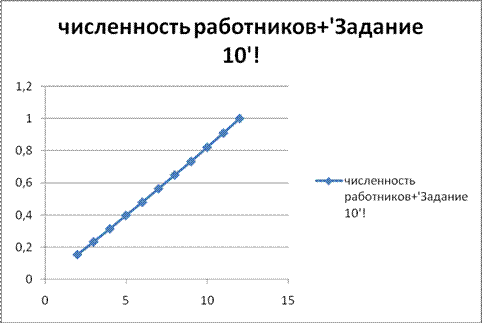
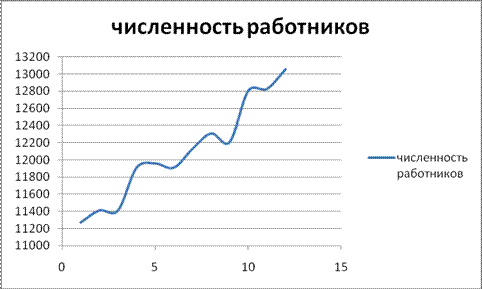
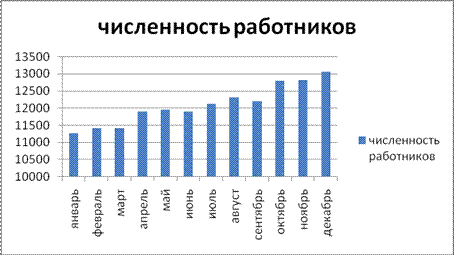
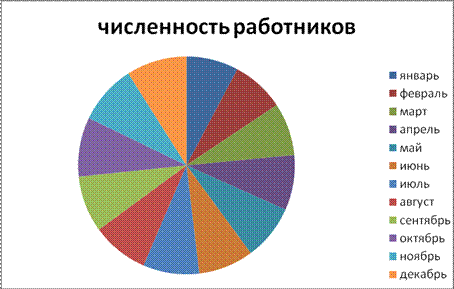
Таким образом, на графиках сразу заметна тенденция к росту численности рабочей силы.
Задание 11 (выводы)
Исследовав показатели выпуска продукции, численности рабочей силы и фондов заработной платы, получилось, что все эти три показателя безусловно связаны достаточно сильной прямой зависимостью. На данном производстве рост выпуска продукции сопровождается ростом численности работников, а раз расширяется штат сотрудников, следовательно, растут фонды заработной платы, но как отмечалось ранее рост каждого показателя проявляется по разному. Возможно это связано с законом уменьшающейся отдачи, то есть каждый дополнительный вовлекаемый в производство работник приносит меньшую полезность предприятию, этим явлением можно объяснить разные темпы роста численности и заработной платы.
|