| 10. Что характеризует средний ресурс? Метод расчета среднего ресурса при малом объеме выборки и больших объемах.
Средний ресурс – показатель долговечности машин одного типа.
Средний ресурс до ремонта – средний ресурс от начала эксплуатации объекта до его первого ремонта.
Средний ресурс между ремонтами - средний ресурс между смежными ремонтами объекта.
Средний ресурс до списания – средний ресурс объекта от начала эксплуатации до его списания, обусловленного предельным состоянием.
Среднее значение ресурса по результатам испытаний находится по формуле
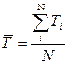
Где Тi
– ресурс i-го объекта (i=1,2,3…)
N - число объектов, взятых под наблюдение.
Задача I-1
Таблица 1
Интервальный статистический ряд эмпирического распределения наработки двигателей СМД-14М до капитального ремонта.
| Границы интервалов, мотто-ч
|
1500-2200
|
2200-2900
|
2900-3600
|
3600-4300
|
4300-5000
|
5000-5700
|
| Частоты 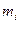 
|
1
|
6
|
17
|
19
|
5
|
2
|
| Частости 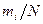
|
0,02
|
0,12
|
0,34
|
0,38
|
0,1
|
0,04
|
| Накопленные частости 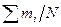
|
0,02
|
0,14
|
0,48
|
0,86
|
0,96
|
1
|
Закон распределения ресурса характеризует связь между его значениями и соответствующими им вероятностями. Наглядное представление о распределение ресурса по отдельным интервальным значениям дает его графическое изображение в виде гистограммы (рис. 1).
На этом же рисунке показан график опытного распределения ресурса, построенный с учетом значений накопленных частостей к концу каждого интервала наработки.
По виду гистограммы и графика значений накопленных частостей можно заключить, что наиболее вероятная наработка двигателей СМД-14М до капитального ремонта находится в интервале значений от 2900 до 4300 мото-ч.
Числовые значения распределения ресурса следующие: среднее значение 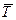 , среднее квадратическое отклонение , среднее квадратическое отклонение 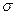 и коэффициент вариации V. Они подсчитываются по следующим выражениям и коэффициент вариации V. Они подсчитываются по следующим выражениям
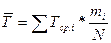
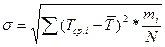
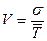
Где 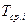 - среднее значение наработки в i-ом интервале, мотто-ч. - среднее значение наработки в i-ом интервале, мотто-ч.
Результаты расчетов:
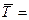 1850*0,02+2550*0,12+3250*0,34+3950*0,38+4650*0,1+5350*0,04=3628 мото-ч 1850*0,02+2550*0,12+3250*0,34+3950*0,38+4650*0,1+5350*0,04=3628 мото-ч
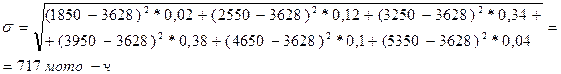
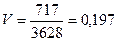
Безразмерный коэффициент вариации V используется не только как относительная характеристика степени рассеивания значения ресурса двигателя СМД-14М относительно среднего значения, но и для выбора его теоретического закона распределения. При этом, если коэффициент вариации V<0.33, то наиболее вероятно нормальное распределение ресурса; если V=0.33…2.0, то может быть распределение Вейбула, если V=1, то вероятным является экспоненциальное распределение.
Реклама

В данной задаче V<0.33, поэтому следует ожидать, что ресурс двигателяСМД-14М распределен по нормальному закону с параметрами 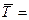 3628 мото-ч и 3628 мото-ч и 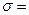 717 мотто-ч. В этом случае вероятность появления ресурсного отказа F(T) – вероятность того, что при наработке от нуля до Т двигатель потребует отправки в капитальный ремонт, равна 717 мотто-ч. В этом случае вероятность появления ресурсного отказа F(T) – вероятность того, что при наработке от нуля до Т двигатель потребует отправки в капитальный ремонт, равна
Вычислим значения F(T) для граничных значений каждого из шести интервалов наработки и по ним построим график теоретического распределения ресурса двигателя СМД-14М.
Таблица 2
Результаты расчета значений вероятности того, что за наработку Т двигатель потребует отправки в капитальный ремонт
| Значение наработки Т, мотто-ч
|
1500
|
2200
|
2900
|
3600
|
4300
|
5000
|
5700
|
| Значения
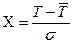
|
-2,969
|
-1,992
|
-1,016
|
-0,039
|
0,938
|
1,914
|
2,891
|
| Значения F(T)
|
0,0017
|
0,028
|
0,158
|
0,344
|
0,828
|
0,971
|
0,998
|
График теоретического распределения ресурса двигателя приведен на рис. 2
На этом же рисунке показано графическое определение 80-ти процентного ресурса двигателя – это наработка, до которой дорабатывают и остаются в работоспособном состоянии 80% двигателей СМД-14М. при этой же наработке 20% двигателей уже достигли предельного состояния, т.е. 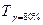 определяется для значения F(T)=0.2. определяется для значения F(T)=0.2.
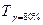 можно установить теоретически, имея в виду, что можно установить теоретически, имея в виду, что
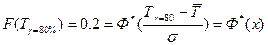
При 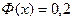 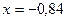
Следовательно,
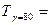 3628-0.84*717=3026 мото-ч 3628-0.84*717=3026 мото-ч
Имея сведения о значениях функции F(T) для граничных значений каждого из шести интервалов наработки (табл. 2), по ним определяется вероятность попадания ресурса в каждый из этих интервалов Pi
и путем деления этой вероятности на ширину интервала устанавливаются значения средней плотности распределения ресурса по каждому интервалу – fi
(T)
Последнее позволяет построить график дифференциальной функции распределения ресурса двигателя – f
(T). При этом полученные среднее значения плотности распределения ресурса fi
(T) на графике откладываются на середине каждого интервала. Данные для построения этого графика приведены в табл. 3, график - на рис. 3.
Таблица 3
Расчет значения средней плотности распределения ресурса двигателя СМД-14М по рассматриваемым интервалам.
| № интервала
|
Граница интервала
|
F(ТВ
)
|
F(TН
)
|
Pi
= F(ТВ
)- F(TН
)
|
fi
(Т)=Pi
/700*10-4
|
Середина интервала (TН
+ТВ
)/2
|
| ТН
|
ТВ
|
| 1
|
1500
|
2200
|
0,028
|
0,0017
|
0,0263
|
0,376
|
1850
|
| 2
|
2200
|
2900
|
0,158
|
0,028
|
0,13
|
1,857
|
2550
|
| 3
|
2900
|
3600
|
0,344
|
0,158
|
0,186
|
2,657
|
3250
|
| 4
|
3600
|
4300
|
0,828
|
0,344
|
0,484
|
6,914
|
3950
|
| 5
|
4300
|
5000
|
0,971
|
0,828
|
0,143
|
2,043
|
4650
|
| 6
|
5000
|
5700
Реклама

|
0,998
|
0,971
|
0,027
|
0,386
|
5350
|
По виду полученного графика можно заключить, что, также как и по гистограмме рис. 1, наиболее вероятная наработка двигателя до предельного состояния находится в интервале от 2550 до 4650 мото-ч.
Таким образом, в данной задаче получены следующие значения показателей долговечности двигателя СМД-14:
Средний ресурс между капитальными ремонтами - 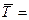 3628 мото-ч 3628 мото-ч
80-процентный гамма-ресурс - 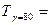 3026 мото-ч 3026 мото-ч
|