|
Метод найменших квадратів
У процесі вивчення різних питань природознавства, економіки і техніки, соціології, педагогіки доводиться на основі великої кількості дослідних даних виявляти суттєві фактори, які впливають на досліджуваний об’єкт, а також встановлювати форму зв’язку між різними зв’язаними одна з одною величинами (ознаками).
Нехай у результаті досліджень дістали таку таблицю деякої функціональної залежності:
Таблиця 1
| x
|
x1
|
x2
|
…
|
xn
|
| y
|
y1
|
y2
|
…
|
yn
|
Треба знайти аналітичний вигляд функції 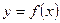 , яка добре відображала б цю таблицю дослідних даних. Функцію , яка добре відображала б цю таблицю дослідних даних. Функцію 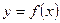 можна шукати у вигляді інтерполяційного поліному. Але інтерполяційні поліноми не завжди добре відображають характер поведінки таблично заданої функції. До того ж значення можна шукати у вигляді інтерполяційного поліному. Але інтерполяційні поліноми не завжди добре відображають характер поведінки таблично заданої функції. До того ж значення 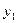 дістають у результаті експерименту, а вони, як правило, сумнівні. У цьому разі задача інтерполювання табличної функції втрачає сенс. Тому шукають таку функцію дістають у результаті експерименту, а вони, як правило, сумнівні. У цьому разі задача інтерполювання табличної функції втрачає сенс. Тому шукають таку функцію 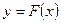 , значення якої при , значення якої при 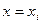 досить близькі до табличних значень досить близькі до табличних значень 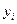 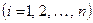 . Формулу . Формулу 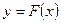 називають емпіричною
, або рівнянням регресії називають емпіричною
, або рівнянням регресії 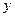 на
на 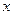 . Емпіричні формули мають велике практичне значення, вдало підібрана емпірична формула дає змогу не тільки апроксимувати сукупність експериментальних даних, «згладжуючи» значення величини . Емпіричні формули мають велике практичне значення, вдало підібрана емпірична формула дає змогу не тільки апроксимувати сукупність експериментальних даних, «згладжуючи» значення величини 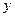 , а й екстраполювати знайдену залежність на інші проміжки значень , а й екстраполювати знайдену залежність на інші проміжки значень 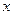 . .
Процес побудови емпіричних формул складається з двох етапів: встановлення загального виду цієї формули і визначення найкращих її параметрів.
Щоб встановити вигляд емпіричної формули, на площині будують точки з координатами 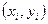 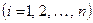 . Деякі з цих точок сполучають плавною кривою, яку проводять так, щоб вона проходила якомога ближче до всіх даних точок. Після цього візуально визначають, графік якої з відомих нам функцій найкраще підходить до побудованої кривої. Звичайно, намагаються підібрати найпростіші функції: лінійну, квадратичну, дробово-раціональну, степеневу, показникову, логарифмічну. . Деякі з цих точок сполучають плавною кривою, яку проводять так, щоб вона проходила якомога ближче до всіх даних точок. Після цього візуально визначають, графік якої з відомих нам функцій найкраще підходить до побудованої кривої. Звичайно, намагаються підібрати найпростіші функції: лінійну, квадратичну, дробово-раціональну, степеневу, показникову, логарифмічну.
Встановивши вигляд емпіричної формули, треба знайти її параметри (коефіцієнти). Найточніші значення коефіцієнтів емпіричної формули визначають методом найменших квадратів
. Цей метод запропонували відомі математики К. Гаусс і А. Лежандр.
Розглянемо суть методу найменших квадратів.
Реклама

Нехай емпірична формула має вигляд
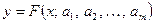 , (1) , (1)
де 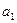 , , 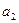 , …, , …, 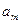 - невідомі коефіцієнти. Треба знайти такі значення коефіцієнтів - невідомі коефіцієнти. Треба знайти такі значення коефіцієнтів 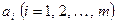 , за яких крива (1) якомога ближче проходитиме до всіх , за яких крива (1) якомога ближче проходитиме до всіх 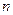 точок точок 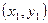 , , 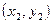 , …, , …, 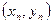 , знайдених експериментально. Зрозуміло, що жодна з експериментальних точок не задовольняє точно рівняння (1). Відхилення від підстановки координат , знайдених експериментально. Зрозуміло, що жодна з експериментальних точок не задовольняє точно рівняння (1). Відхилення від підстановки координат 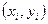 у рівняння (1) дорівнюватимуть величинам у рівняння (1) дорівнюватимуть величинам 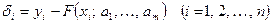 . .
За методом найменших квадратів найкращі значення коефіцієнтів 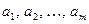 ті, для яких сума квадратів відхилень ті, для яких сума квадратів відхилень
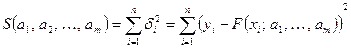 (2) (2)
дослідних даних 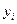 від обчислених за емпіричною формулою (1) найменша. Звідси випливає, що величина (2), яка є функцією від коефіцієнтів від обчислених за емпіричною формулою (1) найменша. Звідси випливає, що величина (2), яка є функцією від коефіцієнтів 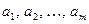 , повинна мати мінімум. Необхідна умов мінімуму функції багатьох змінних ─ її частинні похідні мають дорівнювати нулю, тобто , повинна мати мінімум. Необхідна умов мінімуму функції багатьох змінних ─ її частинні похідні мають дорівнювати нулю, тобто
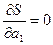 , , 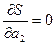 , …, , …, 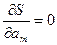 . .
Диференціюючи вираз (2) по невідомих параметрах 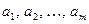 , матимемо відносно них систему рівнянь: , матимемо відносно них систему рівнянь:
 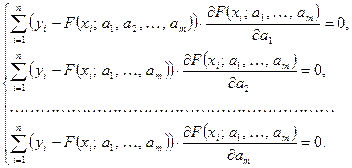
Система (3) називається нормальною
. Якщо вона має розв’язок, то він єдиний, і буде шуканим.
Якщо емпірична функція (1) лінійна відносно параметрів 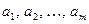 , то нормальна система (3) буде системою з , то нормальна система (3) буде системою з 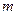 лінійних рівнянь відносно шуканих параметрів. лінійних рівнянь відносно шуканих параметрів.
Будуючи емпіричні формули, припускатимемо, що експериментальні дані 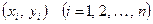 додатні. додатні.
Якщо серед значень 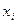 і і 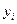 є від’ємні, то завжди можна знайти такі додатні числа є від’ємні, то завжди можна знайти такі додатні числа 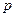 і і 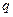 , що , що 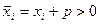 і і 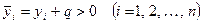 . .
Тому розв’язування поставленої задачі завжди можна звести до побудови емпіричної формули для додатних значень 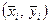 . .
Побудова лінійної емпіричної формули.
Нехай між даними 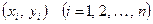 існує лінійна залежність. Шукатимемо емпіричну формулу у вигляді існує лінійна залежність. Шукатимемо емпіричну формулу у вигляді
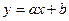 , (4) , (4)
де коефіцієнти 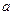 і і 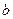 невідомі. невідомі.
Знайдемо значення 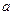 і і 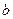 , за яких функція , за яких функція 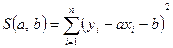 матиме мінімальне значення. Щоб знайти ці значення, прирівняємо до нуля частинні похідні функції матиме мінімальне значення. Щоб знайти ці значення, прирівняємо до нуля частинні похідні функції 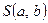
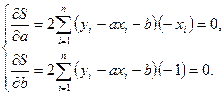
Звідси, врахувавши, що 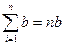 , маємо , маємо
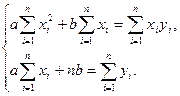 (5) (5)
Розв’язавши відносно 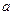 і і 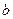 останню систему, знайдемо останню систему, знайдемо
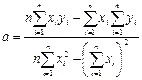 , (6) , (6)
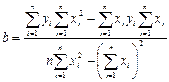 . (7) . (7)
Зазначимо, що, крім графічного, є ще й аналітичний критерій виявлення лінійної залежності між значеннями 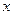 і і 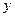 . .
Покладемо 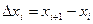 , , 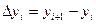 , , 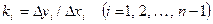 . .
Якщо  , то залежність між , то залежність між 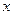 і і 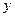 лінійна, бо точки лінійна, бо точки 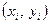 лежатимуть на одній прямій. Якщо лежатимуть на одній прямій. Якщо 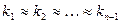 , то між , то між 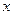 і і 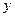 існує майже лінійна залежність, оскільки точки існує майже лінійна залежність, оскільки точки 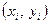 лежатимуть близько до деякої прямої. лежатимуть близько до деякої прямої.
Побудова квадратичної емпіричної залежності.
Нехай функціональна залежність між 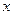 та та 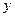 - квадратична. Шукатимемо емпіричну формулу у вигляді - квадратична. Шукатимемо емпіричну формулу у вигляді
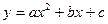 . (8) . (8)
Тоді формулу (2) запишемо наступним чином
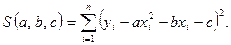
Для знаходження коефіцієнтів 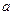 , , 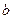 , , 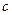 , за яких функція , за яких функція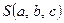 мінімальна, обчислимо частинні похідні мінімальна, обчислимо частинні похідні  , , 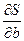 , , 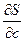 і прирівняємо їх до нуля. В результаті дістанемо систему рівнянь і прирівняємо їх до нуля. В результаті дістанемо систему рівнянь
Реклама

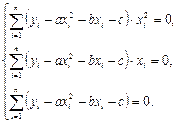
Після рівносильних перетворень маємо систему
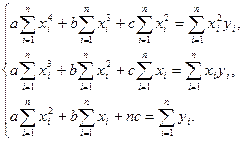 (9) (9)
Розв’язок цієї системи і визначає єдину параболу, яка краще від усіх інших парабол (8) подає на розглядуваному проміжку задану таблично функціональну залежність.
Сформулюємо аналітичний критерій для квадратичної залежності. Для цього введемо поділені різниці першого і другого порядку 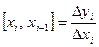
і 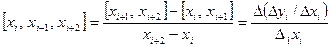 , де , де 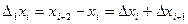 . .
Точки 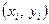 розміщені на параболі (8) тоді і тільки тоді, коли всі поділені різниці другого порядку зберігають сталі значення. розміщені на параболі (8) тоді і тільки тоді, коли всі поділені різниці другого порядку зберігають сталі значення.
Якщо точки 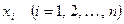 рівновіддалені, тобто рівновіддалені, тобто 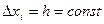 , то для існування квадратичної залежності (8) необхідно і достатньо, щоб була сталою скінчена різниця другого порядку , то для існування квадратичної залежності (8) необхідно і достатньо, щоб була сталою скінчена різниця другого порядку 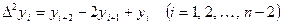 , причому , причому 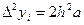 . .
Побудова емпіричних формул найпростіших нелінійних залежностей.
Нехай у системі координат 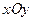 маємо нелінійну залежність маємо нелінійну залежність 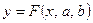 , неперервну і монотонну на відрізку , неперервну і монотонну на відрізку 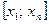 . .
Введемо змінні 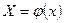 , , 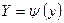 так, щоб у новій системі координат так, щоб у новій системі координат 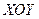 задана емпірична нелінійна залежність стала лінійною задана емпірична нелінійна залежність стала лінійною
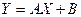 . (10) . (10)
Тоді точки з координатами 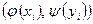 в площині в площині 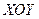 лежатимуть на прямій лінії. лежатимуть на прямій лінії.
Покажемо, як від нелінійних залежностей
 , 2) , 2) 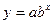 , 3) , 3) 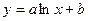 , ,
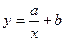 , 5) , 5) 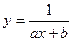 , 6) , 6) 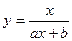
перейти до лінійних.
1) Розглянемо степеневу залежність  , де , де 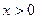 , , 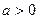 , , 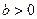 . .
Логарифмуючи її, знаходимо 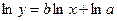 . Звідси, поклавши . Звідси, поклавши 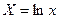 , , 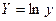 , , 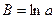 , , 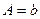 , маємо , маємо 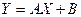 . .
2) Логарифмуючи показникову залежність 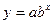 , маємо , маємо 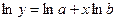 . Поклавши . Поклавши 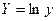 , , 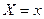 , , 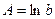 , , 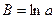 в системі координат в системі координат 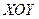 дістанемо залежність (10). дістанемо залежність (10).
Зазначимо, що замість показникової залежності 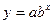 часто шукають залежність часто шукають залежність 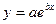 . Остання перетвориться в лінійну, якщо позначити . Остання перетвориться в лінійну, якщо позначити 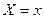 , , 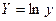 , , 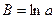 , , 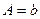 . .
3) Щоб перейти від логарифмічної залежності 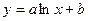 до лінійної до лінійної 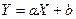 , досить зробити підстановку , досить зробити підстановку 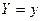 , , 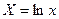 . .
4) У гіперболічній залежності замінимо змінні 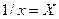 , , 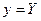 . Тоді гіперболічна залежність перетвориться в лінійну (10), в якій . Тоді гіперболічна залежність перетвориться в лінійну (10), в якій 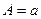 , , 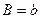 . .
5) Розглянемо дробово-лінійну функцію 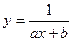 . Знайдемо обернену функцію . Знайдемо обернену функцію 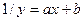 . Тоді ввівши нові координати . Тоді ввівши нові координати 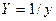 , , 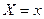 , дістанемо лінійну залежність (10), де , дістанемо лінійну залежність (10), де 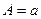 , , 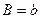 . .
6) Нехай маємо дробово-раціональну залежність 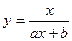 . Оберненою до неї буде залежність . Оберненою до неї буде залежність  . Ввівши нові змінні . Ввівши нові змінні 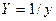 , , 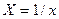 , дістанемо лінійну залежність (10) з коефіцієнтами , дістанемо лінійну залежність (10) з коефіцієнтами 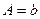 , , 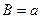 . .
Отже, для побудови будь-якої з емпіричних формул 1)-6) треба:
а) за вихідною таблицею даних 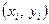 побудувати нову таблицю побудувати нову таблицю 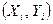 , використавши відповідні формули переходу до нових координат; , використавши відповідні формули переходу до нових координат;
б) за новою таблицею даних знайти методом найменших квадратів коефіцієнти 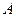 і і 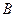 лінійної функції (10); лінійної функції (10);
в) за відповідними формулами знайти коефіцієнти 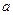 і і 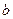 даної нелінійної залежності. даної нелінійної залежності.
Вибрати емпіричну формулу для нелінійних залежностей графічним методом часто буває важко. Тоді вдаються до перевірки аналітичних критеріїв існування певної залежності. Для цього зводять її до лінійної і перевіряють виконання критерію лінійної залежності між перетвореними вихідними даними 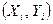 . Але є й власні аналітичні критерії наявності кожної з розглянутих вище нелінійних залежностей. Найпростіші необхідні умови їх наявності подано в табл. 2. . Але є й власні аналітичні критерії наявності кожної з розглянутих вище нелінійних залежностей. Найпростіші необхідні умови їх наявності подано в табл. 2.
Таблиця 2
| № пор.
|
Емпірична формула
|
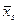
|
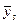
|
Спосіб вирівнювання
|
| 1
|
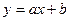
|
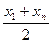
|
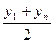
|
|
| 2
|
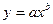
|
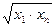
|
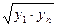
|
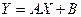 , де , де 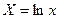 , , 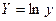 , , 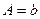 , , 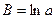
|
| 3
|
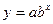
|
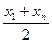
|
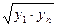
|
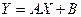 , де , де 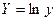 , , 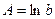 , , 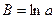
|
| 4
|
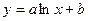
|
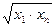
|
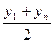
|
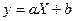 , де , де 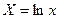
|
| 5
|
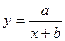
|
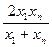
|
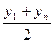
|
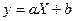 , де , де 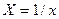
|
| 6
|
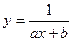
|
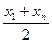
|
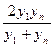
|
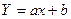 , де , де 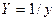
|
| 7
|
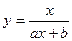
|
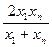
|
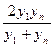
|
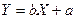 , де , де  , , 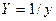
|
Умови перевіряють у такий спосіб. На заданому відрізку зміни незалежної змінної 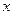 вибирають дві точки, досить надійні і розміщені якомога далі одна від одної. Нехай, наприклад, це будуть точки вибирають дві точки, досить надійні і розміщені якомога далі одна від одної. Нехай, наприклад, це будуть точки 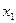 , , 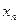 . Потім, залежно від типу емпіричної формули, що перевіряється, обчислюють значення . Потім, залежно від типу емпіричної формули, що перевіряється, обчислюють значення 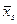 , яке є або середнім арифметичним, або середнім геометричним, або середнім гармонічним значень , яке є або середнім арифметичним, або середнім геометричним, або середнім гармонічним значень 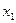 , , 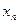 . Маючи значення . Маючи значення 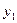 і і 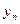 аналогічно обчислюють і відповідне значення аналогічно обчислюють і відповідне значення 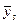 . Далі, користуючись даною таблицею значень . Далі, користуючись даною таблицею значень 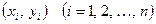 , для значення , для значення 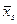 знаходять відповідне йому значення знаходять відповідне йому значення 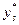 . Якщо . Якщо 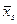 немає в таблиці, то немає в таблиці, то 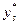 знаходять наближено з побудованого графіка даної залежності або за допомогою лінійної інтерполяції знаходять наближено з побудованого графіка даної залежності або за допомогою лінійної інтерполяції 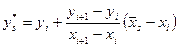 , де , де 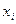 і і 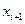 ─ проміжні значення, між якими лежить ─ проміжні значення, між якими лежить  . Обчисливши . Обчисливши 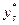 , знаходять величину , знаходять величину  . Якщо ця величина велика, то відповідна емпірична формула не придатна для апроксимації заданих табличних даних. З кількох придатних емпіричних формул перевагу надають тій, для якої відхилення . Якщо ця величина велика, то відповідна емпірична формула не придатна для апроксимації заданих табличних даних. З кількох придатних емпіричних формул перевагу надають тій, для якої відхилення  якомога менше. якомога менше.
|