| ОЦЕНКА ТОЧНОСТИ И НАДЕЖНОСТИ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
Цель работы: по данным результатов измерений найти предварительные значения показателей вариации, оценить пределы возможных ошибок и после исключения ошибочных результатов найти точные показатели вариации, определить величину доверительных интервалов для заданных значений доверительных вероятностей. Сделать выводы.
Исходные данные: варианты заданий приведены в таблице 2.
При проведении измерений, опытов, экспериментов возникают ошибки двух видов: систематические и случайные.
Систематические ошибки связаны с погрешностями измерительных приборов при измерениях.
Случайные ошибки не связаны с измерениями и обусловлены случайными внешними причинами (сбои, отказы аппаратуры, скачки напряжений в сети питания, сейсмические сотрясения, отвлечение внимания оператора, описки в записях и мн. др.)
При однократном измерении ошибка может быть обнаружена только путем логического анализа или сопоставлением результата с априорным представлением о нем. Установив и устранив причину ошибки, измерение можно повторить.
При многократном измерении одной и той же величины ошибки проявляются в том, что результаты отдельных измерений значительно отличаются от остальных. Иногда это отличие настолько большое, что ошибка очевидна, поэтому данный результат можно отбросить как заведомо неверный. Если отличие небольшое, то оно может быть следствием как ошибки, так и рассеяния отсчета. Определить возможность исключения сомнительного результата измерения позволяет «правило трех сигм», которое гласит:
если при многократном измерении одной и той же величины постоянного размера сомнительное значение результата отличается от среднего значения хср
больше, чем на 3σ, то с вероятностью 0,997 оно является ошибочным и его следует отбросить.
При построении вариационных рядов каждый вариант или интервал имеет определенную частость, которая при большом количестве измерений стремится к вероятности попадания значения в данный интервал.
Одной из наиболее распространенных форм распределения случайной величины является нормальное распределение (распределение Гаусса).
С ним приходится сталкиваться при анализе производственных погрешностей, контроле технологических процессов и режимов и т.д.
Реклама

Если весь массив экспериментальных данных подчиняется закону нормального распределения, то все значения измеряемой величины должны группироваться вокруг среднего значения, и выпадение какого-либо отдельного значения результата из этого массива позволяет предположить, что он ошибочный.
Чтобы дать представление о точности и надежности оценки результата пользуются доверительными интервалами и доверительными вероятностями.
Доверительный интервал определяет, на какую величину может отличаться отдельное значение результата измерения при нормальном распределении от своего среднего значения.
Неравенство
P(хср
– ε < x0
< хср
+ε) (1)
означает, что с вероятностью P значение измеряемого параметра x0
попадает в интервал
Ip
= (хср
- ε, хср
+ ε)
Например, известно, что с вероятностью P = 0,5 измеряемое значение при нормальном распределении попадет в интервал
(хср
± 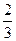 σ); σ);
с P = 0,68 в интервал (хср
± σ)
с P = 0,95 в интервал (хср
± 2σ)
с P = 0,99 в интервал (хср
± 2,6σ)
с P = 0,997 в интервал (хср
± 3σ)
Эта вероятность называется доверительной вероятностью, а интервал – доверительным интервалом.
Доверительный интервал измеряемого параметра x0
приближенно находится по формуле
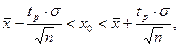 (2) (2)
где tр
определяет число средних квадратичных отклонений, которое нужно отложить вправо и влево от центра рассеивания для того, чтобы вероятность попадания x0
в полученный интервал была равна P;
n – общее количество измерений.
При выборе доверительной вероятности необходимо учитывать ответственность поставленной задачи: чем более ответственна задача, тем с большей доверительной вероятностью (надежностью) должны быть оценены полученные параметры статистического анализа. Обычно для технических расчетов их принимают равными от 0,90 до 0,99, т.е. от 90 до 99%.
доверительный вероятность интервал вариация
Порядок выполнения работы
1. По данным пробной выборки рассчитываем предварительные значения показателей вариации
размах вариации
R = Xmax
– Xmin
. (3)
Средняя арифметическая
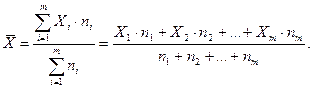 (4) (4)
Дисперсия может быть рассчитана по ранее изученной формуле или по упрощенной формуле, наиболее часто применяемой на практике
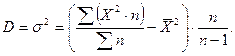 (5) (5)
Среднеквадратическая погрешность
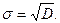 (5) (5)
Коэффициент вариации
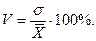 (6) (6)
2. Определяем пределы возможных ошибок. Для этого используем правило «трех сигм». Интервал нахождения истинных значений будет равен
Реклама

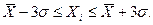 (7) (7)
Найти в ряду значения, которые не попадают в полученный интервал. Эти значения и являются ошибочными, поэтому должны быть отброшены.
3. После удаления из ряда измерений случайных величин производим пересчет показателей вариации. По правилу «трех сигм» определяем пределы возможных ошибок
4. Повторяем п. 3) до тех пор, пока не исключим все ошибки. т.е. все значения будут находиться в интервале (7)
5. После исключения случайных ошибок для каждой заданной доверительной вероятности находим доверительный интервал по формуле
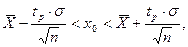 (8) (8)
Параметр tp следует определять по табл. 1 в зависимости от величины заданной доверительной вероятности.
Таблица 1 - Значения коэффициента доверия
| p
|
tp
|
p
|
tp
|
p
|
tp
|
| 0,80
|
1,282
|
0,88
|
1,554
|
0,96
|
2,053
|
| 0,81
|
1,310
|
0,89
|
1,597
|
0,97
|
2,169
|
| 0,82
|
1,340
|
0,90
|
1,643
|
0,98
|
2,325
|
| 0,83
|
1,371
|
0,91
|
1,694
|
0,99
|
2,576
|
| 0,84
|
1,404
|
0,92
|
1,750
|
0,995
|
2,807
|
| 0,85
|
1,439
|
0,93
|
1,810
|
0,997
|
3,290
|
| 0,86
|
1,475
|
0,94
|
1,880
|
|
|
| 0,87
|
1,513
|
0,95
|
1,960
|
|
|
6. Сделать выводы
– какие значения массива экспериментальных данных являются случайными ошибками, и с помощью какого правила определялось наличие ошибок;
– как изменяются показатели вариации после исключения случайных ошибок;
– как изменяется доверительный интервал при изменении доверительной вероятности.
Исходные данные для выполнения задания
| Вариант
|
Задание
|
| 1
|
8,5 7,7 8,4 7,3 8,4 8,4 8,3 7,6 8,7 8,4 8,4 6,1 6,2 7,3 8,4 8,3 7,8 8,3 7,5 2,1 11,2 18,1 8,2 8,7 9,9
Доверительные вероятности: p1
=0,85 p2
=0,95 p3
=0,995
|
| 2
|
22 24 28 22 24 24 24 33 24 25 24 25 24 24 25 27 26 24 25 25 27 12 34
Доверительные вероятности: p1
=0,8 p2
=0,9 p3
=0,99.
|
| 3
|
1,3 1,2 1,2 0,9 0,9 0,8 1,2 1,1 1,2 1,5 0,3 1,2 1,3 1,2 1,2 1,2 1,1 1,2 1,2 1,1 2,1 1,2 1,3
Доверительные вероятности: p1
=0,88 p2
=0,98 p3
=0,997.
|
| 4
|
40 45 44 45 35 46 47 48 43 50 45 47 38 45 44 73 41 44 40 46 44 15 43
Доверительные вероятности: p1
=0,85 p2
=0,99 p3
=0,997.
|
| 5
|
2 11 10 10 9 10 11 10 9 10 10 10 11 10 9 10 11 10 10 11 10 11 19
Доверительные вероятности: p1
=0,8 p2
=0,85 p3
=0,95.
|
| 6
|
8,5 8,3 8,4 8,4 8,4 8,4 8,3 8,5 8,6 8,4 1,8 8,4 8,4 7,4 6,2 8,4 8,4 8,3 14,7 8,3 8,3 8,4 8,3
Доверительные вероятности: p1
=0,95 p2
=0,99 p3
=0,997.
|
| 7
|
8,5 7,7 8,4 1,1 8,4 8,3 7,6 8,7 8,4 7,2 8,4 8,4 6,1 14,5 8,4 8,4 8,3 7,8 8,3 7,5 8,3 7,7 8,8
Доверительные вероятности: p1
=0,86 p2
=0,95 p3
=0,995.
|
| 8
|
8,5 4,2 8,4 8,3 8,4 8,4 8,3 8,6 8,7 8,4 8,2 8,4 8,4 12,3 9,2 8,3 8,4 8,3 8,4 8,3 8,8 8,8 8,5 8,9
Доверительные вероятности: p1
=0,85 p2
=0,99 p3
=0,997.
|
| 9
|
12,5 12,8 13,3 12,8 12,7 13,1 12,6 12,9 13 13,8 14,6 12,9 13 13,1 13,3 12,9 13,3 11,4 12,8 2,1 12,2 22,4 13,3 7,8
Доверительные вероятности: p1
=0,95 p2
=0,99 p3
=0,997.
|
| 10
|
22 24 22 29 24 24 24 24 41 24 25 24 25 24 25 24 25 22 26 24 25 25 8 24
Доверительные вероятности: p1
=0,8 p2
=0,85 p3
=0,9.
|
| 11
|
1,3 1,2 1,1 1,3 1,3 2,4 1,2 1,3 1,2 1,4 0,1 1,2 1,3 1,1 1,2 1,1 1,2 1,3 1,2 1,2 1,2 1,3 1,2 1,2
Доверительные вероятности: p1
=0,83 p2
=0,88 p3
=0,92.
|
| 12
|
2,3 2,2 2,1 2,2 3,8 1,8 2,20 2,2 2,2 2,3 0,8 2,2 2,3 2,2 2,3 2,2 2,3 2,2 2,4 2,5 2,5 2,2 2,3 2,8
Доверительные вероятности: p1
=0,8 p2
=0,9 p3
=0,99.
|
| 13
|
5,3 5,2 5 5,1 4,8 8,8 5,20 5,5 5,2 5,3 5,2 5,5 5,1 5,2 5,3 5,2 2,1 5,5 5,2 5,2 5,5 5,5 5,2 5,3
Доверительные вероятности: p1
=0,9 p2
=0,99 p3
=0,997.
|
| 14
|
10,3 10,2 13,3 10,9 10,9 10,8 10,20 10,1 10,2 10,5 10,2 10,3 10,2 10,2 10,1 10,2 10,2 10,1 10,1 10,2 10,3 7,1 10,4
Доверительные вероятности: p1
=0,8 p2
=0,92 p3
=0,98.
|
| 15
|
23 25 26 21 24 25 23,00 35 24 25 24 25 24 22 25 27 26 22 25 25 21 23 27 11 26 22
Доверительные вероятности: p1
=0,83 p2
=0,88 p3
=0,99.
|
| 16
|
11 12 10 12 10 11 13 22 12 11 14 11 11 13 11 13 14 13 12 10 12 11 12 11 2 17 12
Доверительные вероятности: p1
=0,85 p2
=0,91 p3
=0,98.
|
| 17
|
12 13,8 13,1 11,8 10,7 11,1 12,20 12,1 13,6 12,8 21,1 10,9 13,1 13,3 13,8 11,9 13,3 3,5 11,1 12,3 11 11,3 12,1 11,9
Доверительные вероятности: p1
=0,82 p2
=0,9 p3
=0,96.
|
| 18
|
2,1 2,3 2 2,2 2,5 2,3 2,10 2,3 2,2 2,1 2,3 5,2 2,5 2,1 2,1 2,2 2,2 2,2 2,2 2,2 1,9 5,1 2,1 2,3
Доверительные вероятности: p1
=0,81 p2
=0,91 p3
=0,997.
|
| 19
|
1,1 1,3 1,2 0,95 0,99 1,3 1,10 1,4 1,1 1,7 0,1 1,5 1,2 1,2 1,1 1,2 1,3 1,2 1,2 1,1 1,15 1,2 1,5 2,2
Доверительные вероятности: p1
=0,89 p2
=0,95 p3
=0,97.
|
| 20
|
22,5 22,8 23,3 22,8 22,7 11,5 22,60 22,9 23,1 23,8 24,6 22,9 23 23,1 22,9 23,3 35,5 23,1 25,5 27,1 23,1 22,1 22,3 23,3
Доверительные вероятности: p1
=0,92 p2
=0,98 p3
=0,995.
|
|