| ГЛАВА 2. ВЕКТОРНАЯ АЛГЕБРА.
§1. Основные определения.
При изучении различных физических процессов и явлений нам приходится иметь дело с объектами разной природы. Некоторые величины в физике, механике и технике полностью описываются заданием их числовых
значений. Такими величинами, например, являются длина, объём тела, его масса, температура, электрический заряд и другие.
Эти величины называются скалярными
или просто скалярами.
Однако, чтобы задать такие величины как скорость, ускорение, силу, напряженность магнитного поля и так далее, необходимо указать не только численное значение этой величины, но и её направление в пространстве.
Определение 1.
Величина, для которой указаны ее численное значение и направление
, называется векторной или вектором.
Векторы изображаются направленными прямолинейными отрезками и обозначаются 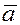 или или 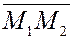 , где точки , где точки 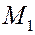 и и 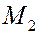 – начало и конец вектора соответственно. Так фиксируется его направление. – начало и конец вектора соответственно. Так фиксируется его направление.
Численное значение векторной величины называется длиной или модулем
вектора и обозначается 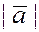 или или 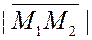 (длина отрезка). (длина отрезка).
Если 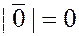 , то , то 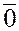 – нулевой вектор; направление нулевого вектора – нулевой вектор; направление нулевого вектора
не определено, т. е. его можно считать произвольным.
Определение 2.
Если задан ненулевой вектор 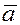 , то единичный вектор того же направления , то единичный вектор того же направления 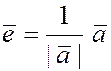 называется ортом
вектора называется ортом
вектора 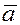 . .
Определение 3.
Два вектора 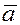 и и  называются коллинеарными
, если они параллельны одной прямой. Это обычно обозначают так называются коллинеарными
, если они параллельны одной прямой. Это обычно обозначают так 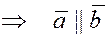 . Нулевой вектор считается коллинеарным любому вектору. . Нулевой вектор считается коллинеарным любому вектору.
Определение 4.
Три вектора называются компланарными
, если они параллельны одной плоскости. Нулевой вектор считается компланарным любой системе компланарных между собой векторов.
Определение 5.
Два вектора равны
, т.е. 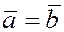 , если выполнены три условия: , если выполнены три условия:
1. модули их равны 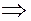 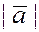 = =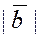 ; ;
2. они параллельны друг другу 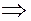 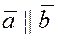 ; ;
3. вектора 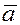 и и  одинаково направлены. одинаково направлены.
Из определения равенства векторов следует, что параллельное перемещение не меняет вектора
. Этим свойством можно пользоваться, чтобы приводить векторы к общему началу, т. е. откладывать их из одной точки. Такие вектора называют свободными
.
§2. Линейные операции над векторами.
Операции сложения
, вычитания векторов и умножения
вектора на скаляр
называются линейными.
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение
Сложение и вычитание векторов.
Сумму двух векторов  и и  можно найти по правилу параллелограмма
. можно найти по правилу параллелограмма
.
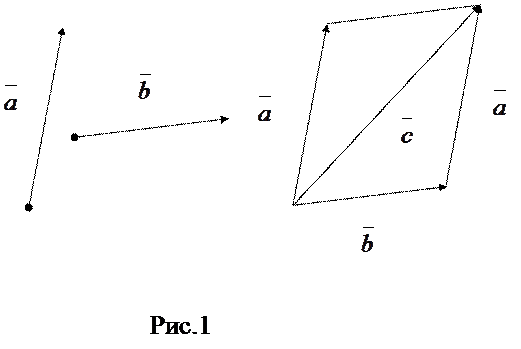
Для этого надо привести их к общему началу и построить на этих векторах параллелограмм
как на сторонах. Тогда диагональ параллелограмма, исходящая из общего начала векторов  и и  и будет их суммой (рис.1). и будет их суммой (рис.1).
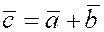 . .
Вычитание
векторов можно выполнять
как сложение вектора 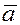 и и 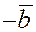 , т.е. , т.е. 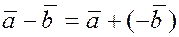 . .
Тогда вторая
диагональ параллелограмма, исходящая из конца вектора  даст нам вектор даст нам вектор 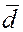 , представляющий собой разность
векторов , представляющий собой разность
векторов 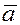 и и  : : 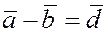 . .
Так как противоположные стороны параллелограмма равны и параллельны, то, учитывая определение равенства двух векторов, сумму векторов 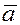 и и  можно представить как третий вектор можно представить как третий вектор 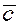 , начало которого совпадает с началом вектора , начало которого совпадает с началом вектора 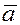 , а конец –
с концом вектора , а конец –
с концом вектора  . .
Такой способ построения суммы
векторов называют правилом треугольника
.
Для этого начало вектора  надо совместить с концом вектора надо совместить с концом вектора 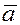 , а затем соединить начало вектора , а затем соединить начало вектора 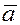 с концом вектора с концом вектора 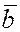 . .
Тогда, как видно из рис.1, получим вектор 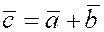 . .
Для нахождения разности векторов приведём
их к общему началу. Соединив их концы, построим треугольник. Тогда имеем 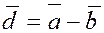 . .
Отсюда легко можно получить правило для нахождения суммы большего числа векторов.
Сумму
нескольких
векторов можно найти по правилу многоугольника: чтобы найти
вектор, представляющий собой сумму
заданных векторов, нужно последовательно совместить
начало следующего вектора-слагаемого с концом
предыдущего, тогда вектор, начало которого совпадает с началом первого вектора, а конец – с концом последнего, будет суммой заданных векторов.
Например, вектор  есть сумма
заданных векторов есть сумма
заданных векторов 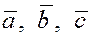 и и  : :
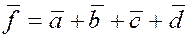 . . Свойства
сложения векторов:
1) 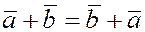 –
переместительное св-во (коммутативность); –
переместительное св-во (коммутативность);
2) 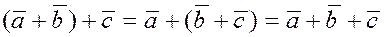 –
сочетательное св-во (ассоциативность). Оба свойства операции сложения векторов следуют непосредственно из определения операции. –
сочетательное св-во (ассоциативность). Оба свойства операции сложения векторов следуют непосредственно из определения операции.
Для любых двух векторов 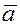 и и 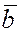 справедливо неравенство треугольника: справедливо неравенство треугольника: 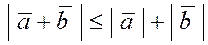 (если векторы (если векторы 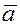 и и 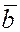 неколлинеарны, то сумма длин двух его сторон больше длины третьей стороны). Очевидно, что это неравенство выполняется и для любого числа векторов, т.е. неколлинеарны, то сумма длин двух его сторон больше длины третьей стороны). Очевидно, что это неравенство выполняется и для любого числа векторов, т.е. 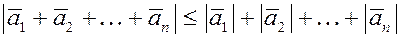 . .
Умножение вектора на скаляр
.
Пусть 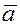 – ненулевой вектор, – ненулевой вектор, 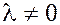 – скаляр. – скаляр.
Произведением
вектора 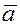 на скаляр на скаляр 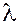 называется вектор называется вектор 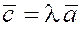 , обладающий следующими свойствами: , обладающий следующими свойствами:
а) 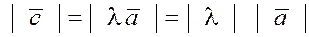 , ,  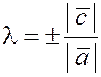 ; ;
б) 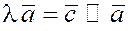 , т.е. они коллинеарны; , т.е. они коллинеарны;
в) 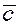 сонаправлен вектору сонаправлен вектору 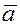 (т.е. направлен одинаково с ним), если (т.е. направлен одинаково с ним), если 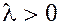 , и направлен в противоположную сторону, если , и направлен в противоположную сторону, если 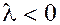 . .
Замечание.
Из определения следует, что
Сервис онлайн-записи на собственном Telegram-боте
Попробуйте сервис онлайн-записи VisitTime на основе вашего собственного Telegram-бота:
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно.
Зарегистрироваться в сервисе
1. вектор 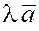 нулевой
, если один из его сомножителей равен нулю; нулевой
, если один из его сомножителей равен нулю;
2. критерий коллинеарности двух векторов:
если 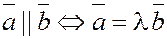 , при , при 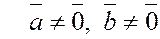 (существует такое (существует такое 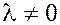 ). ).
Свойства
умножения вектора на скаляр:
1. Перестановочное (или коммутативное) 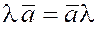
2. Сочетательное (или ассоциативное): 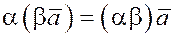 , где , где 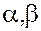 - скаляры. - скаляры.
3. Распределительное (дистрибутивное):
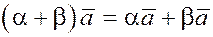 , где , где 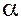 и и 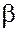 - скаляры; - скаляры;
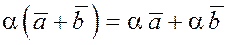 . .
Доказательства этих свойств непосредственно вытекают из определения равенства векторов и сложения векторов.
3.
Линейная зависимость
и независимость векторов
.
Пусть даны векторы 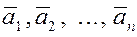 и скаляры и скаляры 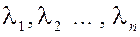 . .
Определение
1.
Вектор
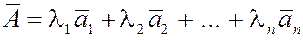 называется линейной
комбинацией
векторов называется линейной
комбинацией
векторов 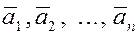 . .
Определение
2.
Векторы 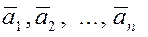 называются линейно независимыми
, если равенство называются линейно независимыми
, если равенство
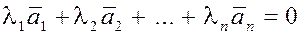
выполняется только
при условии, что 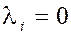 при всех при всех 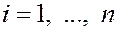
(только при нулевом наборе коэффициентов 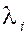 ). ).
Определение
3.
Векторы называются линейно
зависимыми
, если их линейная комбинация обращается в ноль при условии, что хоть один
из скаляров 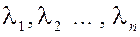 отличен от нуля. отличен от нуля.
Это значит, что среди всех наборов коэффициентов 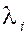 , при которых линейная комбинация обращается в ноль, есть хоть один ненулево
й. , при которых линейная комбинация обращается в ноль, есть хоть один ненулево
й.
Замечание.
Пусть 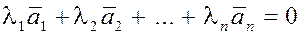 , а какой-то , а какой-то 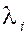 отличен от нуля. Например, пусть отличен от нуля. Например, пусть 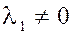 . Тогда имеем . Тогда имеем
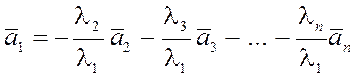 . .
Следовательно, если система векторов 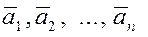 линейно зависима, то, по крайней мере, один из векторов этой системы есть линейная комбинация остальных векторов. линейно зависима, то, по крайней мере, один из векторов этой системы есть линейная комбинация остальных векторов.
Поэтому любые два коллинеарных вектора (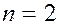 ) линейно зависимы, и любые три компланарных вектора ( ) линейно зависимы, и любые три компланарных вектора (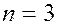 ) тоже линейно зависимы. ) тоже линейно зависимы.
Справедливы и обратные
утверждения: любые два неколлинеарных вектора на плоскости линейно независимы и любые три некомпланарных вектора в пространстве линейно независимы.
Действительно,
если ненулевые векторы 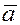 и и 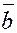 неколлинеарны, то из неколлинеарны, то из 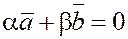 следует следует 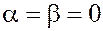 . Иначе есть ненулевой набор коэффициентов . Иначе есть ненулевой набор коэффициентов 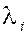 , что противоречит предположению о неколлинеарности. , что противоречит предположению о неколлинеарности.
Если
же
три ненулевых вектора 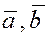 и и 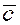 некомпланарны (два вектора всегда компланарны), то из равенства некомпланарны (два вектора всегда компланарны), то из равенства 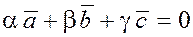 следует, что следует, что 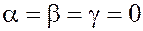 . Иначе опять придём к противоречию: . Иначе опять придём к противоречию:
если, например, 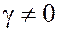 , то , то 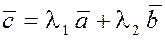 и по определению операции сложения векторов данные вектора и по определению операции сложения векторов данные вектора 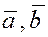 и и 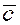 образуют треугольник, через который можно провести плоскость. образуют треугольник, через который можно провести плоскость.
Определение
4.
Любая пара неколлинеарных векторов на плоскости и любая тройка векторов в пространстве называется базисом
множества всех векторов, расположенных соответственно на плоскости или в пространстве.
Сами эти векторы называют базисными векторами
.
Из замечания следует, что, если два компланарных
вектора 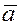 и и 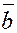 не коллинеарны
, то любой третий вектор не коллинеарны
, то любой третий вектор 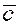 , компланарный с ними, можно представить в виде , компланарный с ними, можно представить в виде 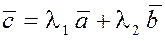 , т.е., как говорят, можно разложить по базису ( , т.е., как говорят, можно разложить по базису (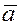 , , 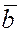 ). Числа ). Числа  и и 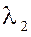 в этом случае называются координатами вектора в этом случае называются координатами вектора
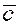 в базисе ( в базисе (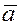 , , 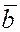 ). . Разложение вектора ). . Разложение вектора 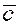 по базису ( по базису (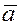 , , 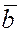 ) единственно, т.е. координаты ) единственно, т.е. координаты  и и 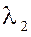 можно найти единственным образом. Покажем это. можно найти единственным образом. Покажем это.
Действительно
.Пусть заданы векторы 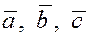 , причем , причем 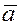 и и 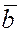 неколлинеарны. Если вектор неколлинеарны. Если вектор 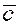 коллинеарен одному из векторов, например, вектору коллинеарен одному из векторов, например, вектору 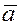 , тогда , тогда 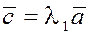 или или 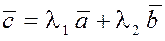 , где , где 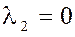 . .
Если вектор 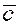 неколлинеарен ни одному из векторов неколлинеарен ни одному из векторов 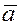 и и 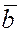 , то приведём вектора , то приведём вектора 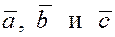 к одному началу к одному началу  . Продолжим прямые, на которых лежат вектора . Продолжим прямые, на которых лежат вектора 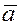 и и 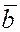 , а затем проведем прямые, параллельные векторам , а затем проведем прямые, параллельные векторам 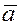 и и 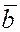 через конец вектора через конец вектора 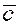 , достроив таким образом параллелограмм OPQR
.
. Вектор , достроив таким образом параллелограмм OPQR
.
. Вектор 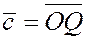 является диагональю параллелограмма. Тогда по правилу параллелограмма имеем является диагональю параллелограмма. Тогда по правилу параллелограмма имеем 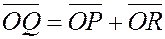 , но , но
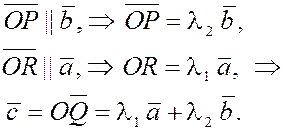
Из построения следует и единственность
такого разложения вектора по базису 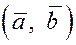 . Количество базисных векторов называется размерностью
векторного пространства: так плоскость называется двумерным пространством и обозначается . Количество базисных векторов называется размерностью
векторного пространства: так плоскость называется двумерным пространством и обозначается 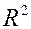 . .
Любые три некомпланарных
вектора 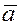 , , 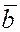 , , 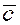 в пространстве линейно независимы и образуют базис трехмерного пространства в пространстве линейно независимы и образуют базис трехмерного пространства 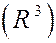 ; всякий
четвертый
вектор ; всякий
четвертый
вектор 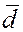 этого пространства можно единственным
образом разложить по базису ( этого пространства можно единственным
образом разложить по базису (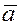 , , 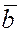 , , 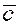 ), т.е. представить в виде ), т.е. представить в виде 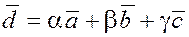 , где a, b, g – координаты вектора , где a, b, g – координаты вектора 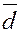 в базисе ( в базисе (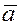 , , 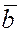 , , 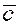 ),. ),.
Доказательство
можно провести аналогично предыдущим рассуждениям.
Определение 5.
Три некомпланарных вектора 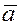 , , 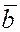 , , 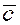 называются правой
тройкой векторов, если из конца третьего
вектора ( называются правой
тройкой векторов, если из конца третьего
вектора (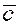 ) кратчайший поворот от первого
вектора ( ) кратчайший поворот от первого
вектора (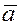 ) ко второму
вектору ( ) ко второму
вектору (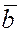 ) виден происходящим ) виден происходящим
в положительном направлении (против часовой стрелки).
И, соответственно, – левой
тройкой, если по часовой стрелке.
§
4. Проекция вектора на ось.
Проекцией
точки
А
на заданную ось называется точка, которая является основание перпендикуляра
, опущенного из точки А
на ось.
Проекцию точки на ось можно также определить как точку пересечения оси с проектирующей
плоскостью, т. е. с плоскостью, проведённой через данную точку перпендикулярно оси.
Пусть в пространстве заданы два вектора 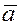 и и 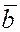 . .
Приведём их к общему началу. Углом между векторами 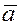 и и 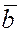 называется наименьший угол, на который надо повернуть один из векторов, называется наименьший угол, на который надо повернуть один из векторов,
чтобы его направление совпало с направлением другого вектора. Из этого определения следует, что 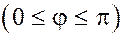 . .
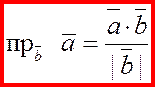
Пусть дан вектор  и некоторая ось и некоторая ось 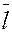 . Опустим из точек . Опустим из точек 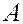 и и 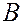 перпендикуляры на ось перпендикуляры на ось 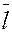 и обозначим проекции этих точек на ось и обозначим проекции этих точек на ось 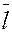 через через 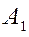 и и 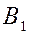 , соотвественно. Получим вспомогательный вектор , соотвественно. Получим вспомогательный вектор 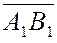 . . Определение 1.
Проекцией вектора  на ось на ось 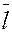 называется длина отрезка называется длина отрезка 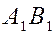 , взятая со знаком плюс
, если вектор , взятая со знаком плюс
, если вектор 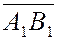 и ось и ось 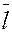 одинаково направлены, и со знаком минус, если они направлены в разные стороны. одинаково направлены, и со знаком минус, если они направлены в разные стороны.
Проекцию вектора 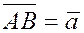 на ось на ось 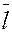 будем обозначать следующим образом: будем обозначать следующим образом: 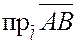 или или 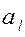 . .
Очевидно, что 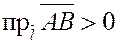 , если угол между векторами , если угол между векторами  и и 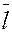 острый, и острый, и 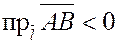 , если угол между векторами , если угол между векторами  и и 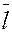 – тупой. – тупой.
Проекцию можно вычислить по формуле
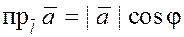 , ,
где 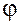 – угол наклона вектора – угол наклона вектора 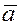 к оси к оси 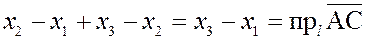 . .
Теорема 1
.
Проекция суммы двух векторов на ось равна сумме проекций слагаемых векторов на ту же ось.
Доказательство
.
Пусть 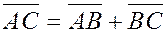 . Обозначим через . Обозначим через 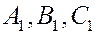 проекции на ось проекции на ось 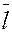 точек A
,
B
и C
соответственно. Пусть точки точек A
,
B
и C
соответственно. Пусть точки 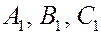 имеют по оси имеют по оси 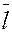 соответственно координаты соответственно координаты 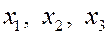 . Тогда . Тогда
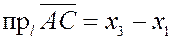 , , 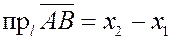 и и 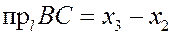
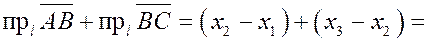 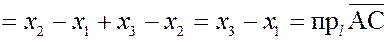 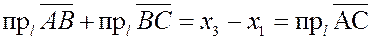 , ,
что и требовалось доказать.
Эта теорема легко обобщается на случай любого числа слагаемых.
Теорема 2
.
Если вектор 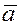 умножить на число умножить на число 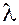 , то и его проекция на ось умножится на число , то и его проекция на ось умножится на число 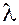 . .
Доказательство
.
Заметим, что если 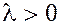 , то вектор , то вектор 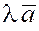 направлен в ту же сторону, что и вектор направлен в ту же сторону, что и вектор 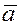 и составляет с осью и составляет с осью 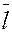 тот же угол тот же угол 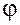 , что вектор , что вектор 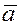 . Если . Если 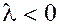 , то вектор , то вектор 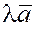 направлен противоположно вектору направлен противоположно вектору 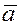 и составляет с осью и составляет с осью 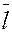 угол ( угол (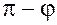 ). ).
1). Пусть 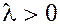 , тогда по формуле , тогда по формуле
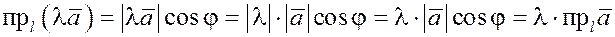 . .
2)пусть 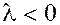 , тогда по формуле , тогда по формуле
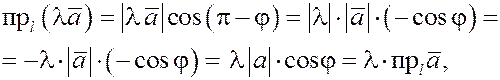
что и требовалось доказать.
Следствие
.
Проекция разности двух векторов на ось 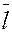 равна разности проекций этих векторов на ту же ось. равна разности проекций этих векторов на ту же ось.
Произведение проекции вектора 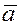 на ось на ось 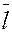 на единичный вектор этой оси (его называют ортом
) называется составляющей вектора
по оси на единичный вектор этой оси (его называют ортом
) называется составляющей вектора
по оси 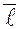 . .
§5. Координаты вектора в декартовом базисе
Определение
1.
Три некомпланарных вектора 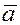 , , 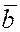 , , 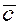 называются правой
тройкой векторов, если из конца третьего
вектора ( называются правой
тройкой векторов, если из конца третьего
вектора (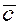 ) кратчайший поворот от первого
вектора ( ) кратчайший поворот от первого
вектора (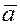 ) ко второму
вектору ( ) ко второму
вектору (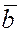 ) виден происходящим в положительном направлении (против часовой стрелки) и левой
тройкой в противном случае. ) виден происходящим в положительном направлении (против часовой стрелки) и левой
тройкой в противном случае.
Мы уже говорили, что ортом
ненулевого вектора 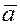 называется единичный вектор называется единичный вектор 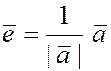 , направленный одинаково
с вектором , направленный одинаково
с вектором 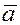 . .
Выберем в пространстве произвольную точку 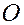 и проведём через неё три взаимно перпендикулярные оси. Перенумеруем их. Ось с выбранным на ней началом отсчёта и единицей длины называется координатной
осью. и проведём через неё три взаимно перпендикулярные оси. Перенумеруем их. Ось с выбранным на ней началом отсчёта и единицей длины называется координатной
осью.
Упорядоченная система (т.е. перенумерованная система) трёх взаимно перпендикулярных координатных осей с общим началом отсчёта и общей единицей длины называется прямоугольной
системой координат в пространстве (её называют также декартовой
системой координат или ортогональной
системой координат).
В этой системе координат первую ось будем называть осью абсцисс
(или осью 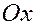 ), вторую – осью ординат
(или осью ), вторую – осью ординат
(или осью 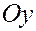 ), третью – осью аппликат
(или осью ), третью – осью аппликат
(или осью 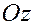 ). ).
Плоскости, содержащие любые две координатные оси будем называть координатными плоскостями:
плоскостью 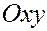 или или 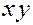 , если она содержит оси , если она содержит оси 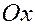 и и 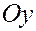 , ,
плоскостью 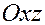 или или 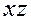 , если она содержит оси , если она содержит оси 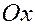 и и 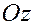 , ,
плоскостью 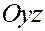 или или 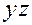 , если она содержит оси , если она содержит оси 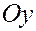 и и 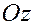 . .
Эти плоскости будут перпендикулярны координатным осям 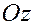 , , 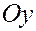 и и 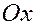 соответственно. соответственно.
Введём единичные векторы 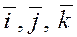 , направления которых совпадают с положительным направлением соответственно осей , направления которых совпадают с положительным направлением соответственно осей 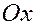 , , 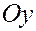 , , 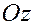 , т.е. , т.е.
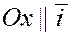 , , 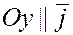 , , 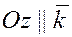 . .
Векторы 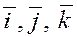 в дальнейшем будем называть ортами
осей прямоугольной или декартовой системы координат. в дальнейшем будем называть ортами
осей прямоугольной или декартовой системы координат.
Различают правую и левую координатные системы. В дальнейшем будем использовать правую систему координат.
Векторы 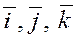 некомпланарны и, следовательно, образуют базис трёхмерного пространства. Эти векторы взаимно перпендикулярны и модули их равны единице некомпланарны и, следовательно, образуют базис трёхмерного пространства. Эти векторы взаимно перпендикулярны и модули их равны единице
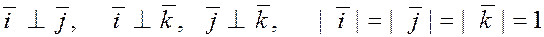 . .
Такая система базисных векторов называется ортогональной
и нормированной
.
Иногда говорят, что правая тройка взаимно ортогональных ортов 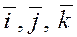 образует декартов базис. образует декартов базис.
Рассмотрим произвольный вектор 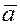 и найдем проекции этого вектора на оси координат. Эти проекции будем называть координатами
вектора и найдем проекции этого вектора на оси координат. Эти проекции будем называть координатами
вектора 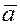 в декартовом базисе в декартовом базисе 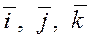 . .
Поместим начало вектора 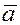 в точку O
. Тогда в точку O
. Тогда  . .
Проведем через конец вектора OM
плоскости, параллельные координатным плоскостям. Они отсекут на координатных осях отрезки, которые представляют собой проекции вектора OM
на соответствующие координатные оси. В результате такого построения получим прямоугольный параллелепипед, одной из диагоналей которого является вектор  . .
По правилу сложения векторов 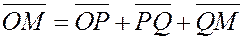 , ,
но 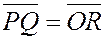 , , 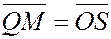 . .
Следовательно,
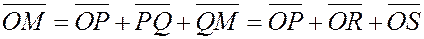 . . Рис.4
В правой части стоят составляющие вектора 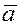 по осям координат: по осям координат:
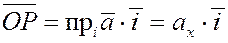 , , 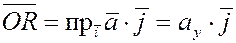 , ,
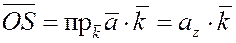 , ,
Тогда разложение вектора 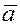 по ортам декартовой системы координат запишется в виде по ортам декартовой системы координат запишется в виде
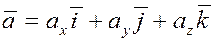 . .
Часто используется более короткое обозначение 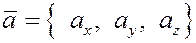 . .
Зная проекции вектора 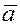 на координатные оси, можно легко найти на координатные оси, можно легко найти 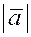 . Действительно
, так как квадрат диагонали прямоугольного параллелепипеда равен сумме
квадратов его сторон, то . Действительно
, так как квадрат диагонали прямоугольного параллелепипеда равен сумме
квадратов его сторон, то 
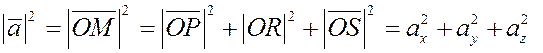 
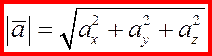 . .
Вектор 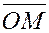 ( (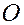 – начало координат) называется радиус-вектором точки M
. Координатами – начало координат) называется радиус-вектором точки M
. Координатами 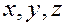 точки точки 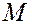 в пространстве называются проекции её радиуса-вектора в пространстве называются проекции её радиуса-вектора 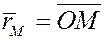 на координатные оси , т.е. координаты вектора на координатные оси , т.е. координаты вектора 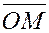 совпадают с координатами точки M совпадают с координатами точки M
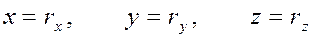 . .
Заметим, что радиус-вектор точки является связанным
вектором, так как его начало всегда
совпадает с началом координат.
Пусть 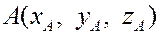 и и 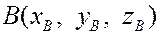 – точки пространства. Найдем координаты вектора – точки пространства. Найдем координаты вектора 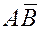 . По правилу сложения векторов имеем . По правилу сложения векторов имеем
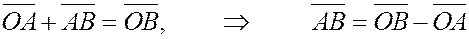 , ,

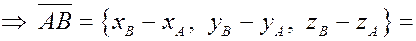
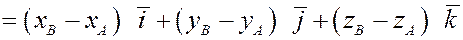 . .
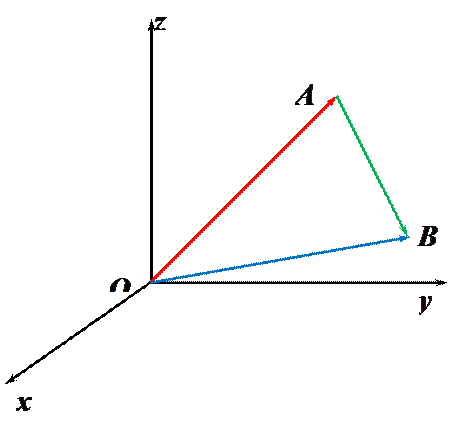
Рис. 5
Таким образом, проекции вектора на координатные оси равны разностям
соответствующих координат конца
и начала
вектора.
Теперь мы можем определить расстояние между двумя точками
пространства как длину соответствующего вектора
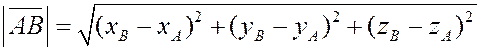
Вспомним основные теоремы о проекциях. Пусть даны два вектора 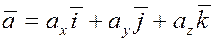 , , 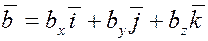 и скаляр и скаляр 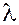 . Тогда из свойств проекций вектора на ось следует . Тогда из свойств проекций вектора на ось следует
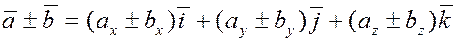
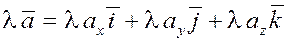
Пусть 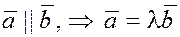 . Проектируя это равенство на оси координат, получим . Проектируя это равенство на оси координат, получим 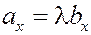 , , 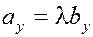 , , 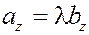 . Следовательно, одноимённые координаты у этих векторов пропорциональны . Следовательно, одноимённые координаты у этих векторов пропорциональны
 . .
Это условие коллинеарности
векторов в координатной форме.
Косинусы углов, которые вектор 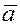 образует с осями координат, называются направляющими косинусами
вектора образует с осями координат, называются направляющими косинусами
вектора 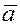 . .
 , ,
где 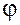 – угол между вектором – угол между вектором 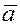 и осью и осью 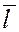 . .
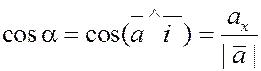 ; ; 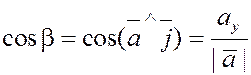 ; ; 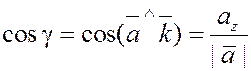 , ,
где 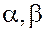 и и 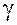 – углы между вектором – углы между вектором 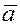 и осями и осями 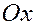 , , 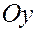 и и 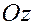 соответственно. соответственно.
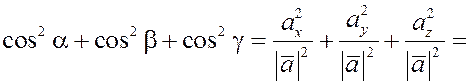
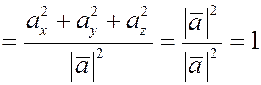 , ,
таким образом,
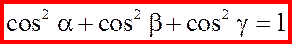 . .
§6. Скалярное произведение двух векторов
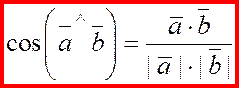
Определение.
Скалярным произведением
двух векторов 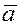 и и 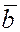 называется произведение их модулей на косинус угла между ними (т.е. число или скаляр): называется произведение их модулей на косинус угла между ними (т.е. число или скаляр):
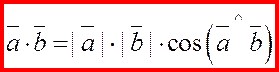 . .
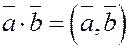
Свойства
скалярного произведения двух векторов:
1) Из определения следует переместительное свойство
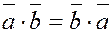 ; ;
2) Скалярное произведение равно нулю, т.е.
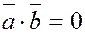 или или 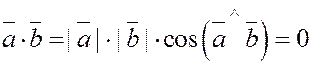
в двух следующих случаях:
а) 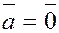 или или 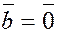
б) 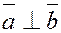 (ортогональны) (ортогональны)
Таким образом, равенство нулю скалярного произведения двух векторов является необходимым
и достаточным
условием
их перпендикулярности
(или ортогональности) 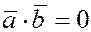 . .
3) Рассмотрим скалярное произведение двух коллинеарных векторов.
Если 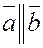 , то , то 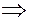  . Если же . Если же 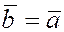 , то мы имеем скалярное произведение вектора , то мы имеем скалярное произведение вектора 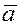 самого на себя самого на себя 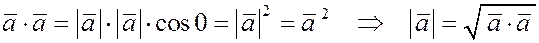 . .
Скалярное произведение вектора самого на себя называется скалярным квадратом и обозначается 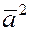 . .
4) Распределительное свойство
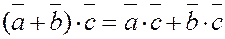 . .
Действительно, заметим, что
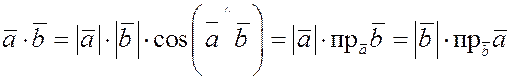 . .
Тогда
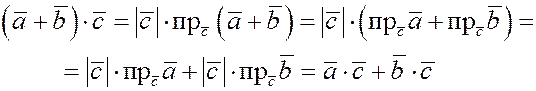
5) Если 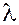 – скаляр, то – скаляр, то 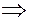 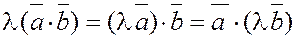 . .
6) Непосредственно из определения операции скалярного умножения векторов следуют формулы
 ; ;  , ,
7) Для базисных векторов 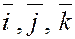 справедливы равенства: справедливы равенства:
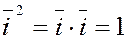 ; ; 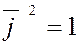 ; ; 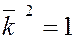 ; ; 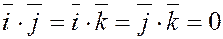 . .
8) Найдём теперь выражение для скалярного произведения в координатной форме.
Пусть 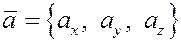 , , 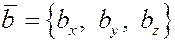 . Скалярное произведение . Скалярное произведение
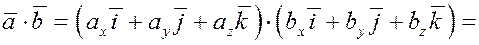
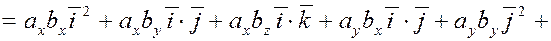
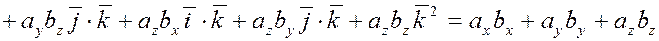 Таким образом, Таким образом,
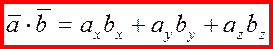 . .
Условие ортогональности векторов в координатной форме:
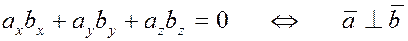 . .
Замечание.
Выясним механический смысл скалярного произведения.
Пусть под действием постоянной силы 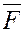 точка перемещается по прямой из положения точка перемещается по прямой из положения  в положение в положение 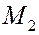 . Сила . Сила 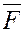 образует с прямой образует с прямой 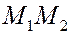 угол угол 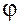 . Работа силы . Работа силы 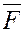 на этом перемещении равна на этом перемещении равна
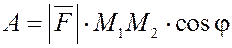 . .
Если ввести вектор перемещения 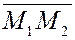 , то выражение для работы можно переписать в виде , то выражение для работы можно переписать в виде
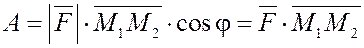 . .
Следовательно, работа силы 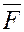 равна скалярному произведению вектора силы на вектор перемещения. равна скалярному произведению вектора силы на вектор перемещения.
§7. Векторное произведение векторов
Векторным произведением вектора  на вектор на вектор 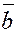 называется вектор называется вектор 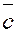 , который определяется следующим образом: , который определяется следующим образом:
а)  , ,
т.е. 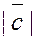 численно равен площади параллелограмма, построенного на перемножаемых векторах как на сторонах; численно равен площади параллелограмма, построенного на перемножаемых векторах как на сторонах;
б) 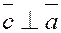 и и 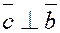 , т.е. он перпендикулярен плоскости, в которой лежат перемножаемые векторы; , т.е. он перпендикулярен плоскости, в которой лежат перемножаемые векторы;
в) 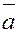 , , 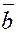 , , 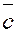 образуют правую
тройку векторов, то есть, если из конца вектора ( образуют правую
тройку векторов, то есть, если из конца вектора (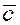 ) кратчайший поворот от вектора ( ) кратчайший поворот от вектора (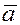 ) к вектору ( ) к вектору (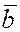 ) виден происходящим против хода часовой стрелки. ) виден происходящим против хода часовой стрелки.
Векторное произведение
векторов 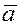 и и 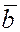 обозначается обозначается
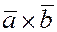 или или 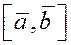 . .
Рис. 6.
Свойства векторного умножения векторов
1.  . .
Т.к. 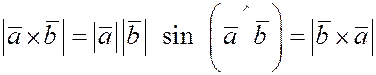 , ,
причем векторы 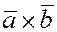 и и 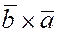 коллинеарны, но направлены противоположно. коллинеарны, но направлены противоположно.
2. 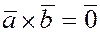 , если , если 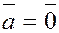 или или 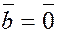 или или 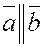 . .
Действительно, если оба вектора ненулевые, то при
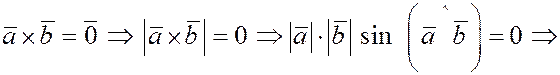
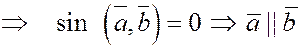 . .
В частности 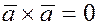 для любого вектора для любого вектора  . .
Таким образом, для коллинеарности двух ненулевых векторов необходимо и достаточно, чтобы их векторное произведение было бы равно нулю.
3. Ассоциативность (или сочетательность) относительно скалярного множителя: если 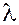 – скаляр, то справедливо равенство – скаляр, то справедливо равенство
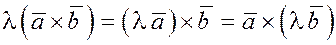 . .
Действительно.
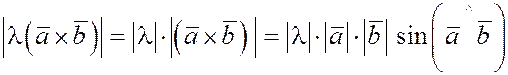
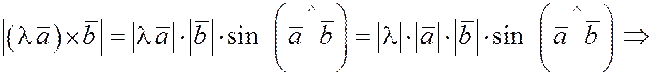
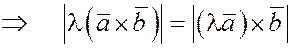 . .
Пары векторов 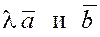 и и 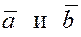 лежат в одной плоскости, лежат в одной плоскости, 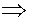  . Также легко можно убедиться в справедливости и второй части равенства. . Также легко можно убедиться в справедливости и второй части равенства.
4. Дистрибутивность относительно сложения векторов:
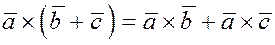 . .
5. Векторные произведения координатных ортов.
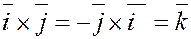 , , 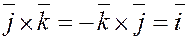 , , 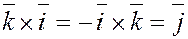 ; ;
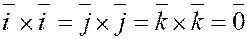 , ,
где 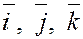 – координатные орты; – координатные орты;
6. Найдем теперь координаты векторного произведения векторов в декартовом базисе 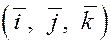 . .
Пусть 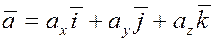 и и 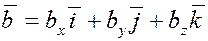 . .
Используя уже рассмотренные свойства, получим
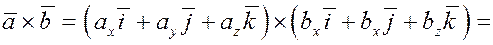
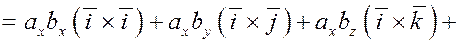
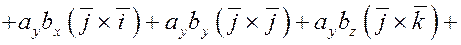
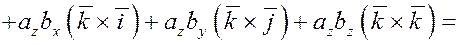
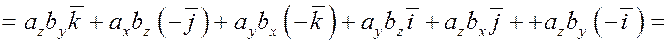
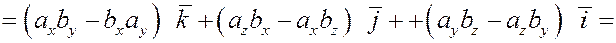
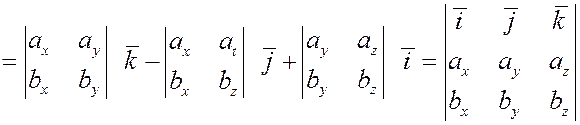
Итак, если 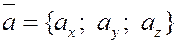 и и 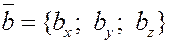 , то , то
 . .
§8.
Смешанное произведение трех векторов.
Если взять вектор 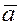 и умножить его векторно на вектор и умножить его векторно на вектор 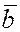 , а затем полученный вектор скалярно умножить на третий вектор , а затем полученный вектор скалярно умножить на третий вектор 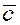 , то получим векторно-скалярное или смешанное произведение трёх векторов. , то получим векторно-скалярное или смешанное произведение трёх векторов.
Определение.
Смешанным
произведением трех векторов 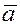 , , 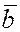 и и 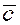 называется скалярное произведение вектора называется скалярное произведение вектора 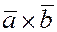 на вектор на вектор 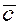 . Смешанное произведение векторов обозначается так . Смешанное произведение векторов обозначается так 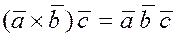 . .
Свойства
смешанного произведения.
1. 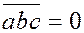 , тогда и только тогда, когда векторы компланарны. , тогда и только тогда, когда векторы компланарны.
2. Выясним геометрический смысл
смешанного произведения. Смешанное произведение
некомпланарных отличных от нуля векторов 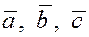 по абсолютной величине равно объему параллелепипеда, построенного на векторах по абсолютной величине равно объему параллелепипеда, построенного на векторах 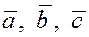 . .
Покажем это. Приведём все три вектора к одному началу и построим на них параллелепипед. Пусть основанием параллелепипеда является параллелограмм, построенный на векторах 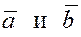 . Площадь этого параллелограмма . Площадь этого параллелограмма 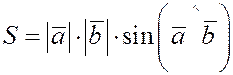 . Обозначим через . Обозначим через 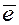 единичный вектор, перпендикулярный плоскости основания нашего параллелепипеда, а через единичный вектор, перпендикулярный плоскости основания нашего параллелепипеда, а через 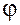 – угол между векторами – угол между векторами 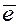 и и 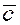 . Тогда . Тогда 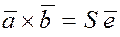 . Скалярное произведение векторов . Скалярное произведение векторов 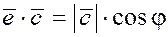 , взятое по абсолютной величине, равно высоте h
нашего параллелепипеда (если тройка векторов правая, то , взятое по абсолютной величине, равно высоте h
нашего параллелепипеда (если тройка векторов правая, то 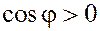 , а если вектора , а если вектора  , ,  и и 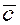 образуют левую тройку векторов, то образуют левую тройку векторов, то 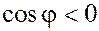 ). ).
Объем параллелепипеда
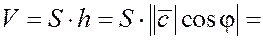
=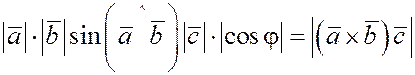 . .
Очевидно, что правая и левая части этого равенства равны по абсолютной величине и имеют одинаковые знаки.
Таким образом, смешанное произведение трёх векторов есть число, модуль которого равен объёму параллелепипеда, построенного на данных векторах. Это число положительное, если векторы образуют правую тройку векторов и отрицательное в противном случае.
3. Круговая перестановка сомножителей в смешанном произведении не меняет его величины, так как при круговой перестановке векторов правая тройка векторов остаётся правой, а левая – левой, т. е. 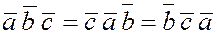 . .
4. Из определения смешанного произведения и векторного произведения следует, что при перестановке местами двух соседних сомножителей смешанного произведения оно меняет знак, так как при такой перестановке векторов правая тройка становится левой, а левая – правой, то есть
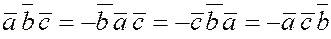 . .
5. Найдем смешанное произведение трех векторов, заданных разложениями в декартовом базисе.
Пусть
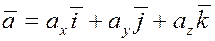 , , 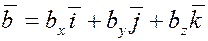 и и 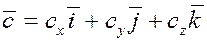 . .
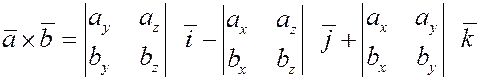 . .
Следовательно,
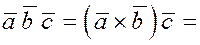
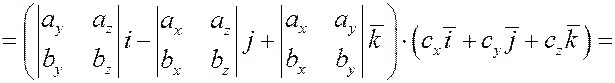
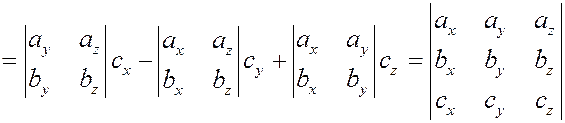 . .
Итак, 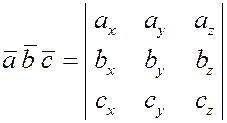 . .
|