| Оглавление
Введение
. 2
1 Магнитная цепь двигателя. Размеры, конфигурация, материал
.. 3
1.1 Главные размеры.. 3
1.2 Сердечник статора. 5
1.3 Сердечник ротора. 6
2. Обмотка статора
. 7
2.1 Параметры, общие для любой обмотки. 7
2.2 Обмотка статора с трапецеидальными полузакрытыми пазами. 9
3. Обмотка короткозамкнутого ротора
. 13
4. Расчёт магнитной цепи.
15
4.1 МДС для воздушного зазора. 15
4.2 МДС при прямоугольных полуоткрытых пазах статора. 15
4.2 МДС при бутылочных пазах ротора.
16
4.3 МДС для спинки статора. 17
4.5 Параметры магнитной цепи. 18
5. Активные и индуктивные сопротивления обмоток
. 20
5.1 Сопротивление обмотки статора. 20
5.2 Сопротивление обмотки короткозамкнутого ротора. 22
5.3 Сопротивление обмоток преобразованной схемы замещения двигателя (с вынесенным на зажимы намагничивающим контуром). 25
7. Круговая диаграмма и рабочие характеристики.
31
Результаты расчёта рабочих характеристик двигателя.
34
Выполнение двухслойной обмотки
.. 35
ПРИЛОЖЕНИЕ А: схема двухслойной обмотки
ПРИЛОЖЕНИЕ Б: круговая диаграмма
ПРИЛОЖЕНИЕ В
:
рабочие характеристики
Введение
Электромашиностроение прошло большой путь развития, начиная от простейших моделей, созданных полтора века назад, до современных электродвигателей и генераторов.
Начиная с середины двадцатых годов, советские электромашиностроители приступили к созданию новых отечественных конструкций, а также к разработке теоретических вопросов и проведению исследований, связанных с проектированием машин. К середине тридцатых годов был создан и внедрён в производство ряд серий асинхронных двигателей, синхронных машин и машин постоянного тока. Развившиеся и окрепшие к этому периоду электромашиностроительные заводы выпускали разные серии машин, с несовпадающими техническими данными, конструкцией и технико-экономическими показателями, что влекло за собой затруднения для потребителей в части замены, ремонта и создания резерва машин.
  Расчёт асинхронного двигателя с короткозамкнутым ротором производим на основании [1]. Расчёт асинхронного двигателя с короткозамкнутым ротором производим на основании [1].
1 Магнитная цепь двигателя. Размеры, конфигурация, материал
1.1 Главные размеры
Высоту оси вращения асинхронного двигателя определяем по таблице 9 – 1 на основании n1
и Рн.
Реклама

Для Рн
=85 кВт.
n1
=1000об/мин.
h=280 мм, 2р=6.
Наружный диаметр сердечника DН1
при стандартной высоте оси вращения h=225 мм выбираем из таблицы 9-2. При данных условиях DН1
=406мм.
Для определения внутреннего диаметра сердечника статора D1
воспользуемся зависимостью D1
=f(DН1
) приведённой в таблице 9 – 3. Для DН1
=520 мм;
D1
=0,72 DН1
–3; (1.1)
D1
=0,72∙520–3 = 371,4 мм.
Принимаем D1
= 225 мм.
Из рисунка 9 – 1 найдём среднее значение кн
=f(P2
) асинхронных двигателей:
Для Рн
=85 кВт;
kн
=0,975.
Для двигателей с короткозамкнутым ротором исполнения по защите IP44 предварительные значения h¢ по рисунку 9-2.
Для Рн
=85 кВт;
h¢=0,93.
 Для двигателей с короткозамкнутым ротором исполнения по защите IP44 принимаем значение cos j¢ по рисунку 9 – 3,а при 2р = 6. Для двигателей с короткозамкнутым ротором исполнения по защите IP44 принимаем значение cos j¢ по рисунку 9 – 3,а при 2р = 6.
cos j¢=0,87.
Расчётная мощность для двигателей переменного тока определяется по формуле
; (1.2)
где РН
– номинальная мощность на валу;
h¢ – КПД;
cos j¢ – коэффициент мощности при номинальной нагрузке.
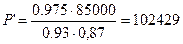 Вт. Вт.
8.Для нахождения линейной нагрузки обмотки статора А1
¢ воспользуемся рисунком 9 – 4 а. и таблицей 9 – 5.
А1
¢ =445 × 0,915=407,175 А/см.
При нахождении максимального значения магнитной индукции в воздушном зазоре будем использовать рисунок 9 – 4б. и таблицу 9 – 5.
Вd
¢=0,76 · 1,04=0,7904 Тл.
Для определения длины сердечника статора зададимся предварительным значением обмоточного коэффициента, при 2р=6
Kоб1
¢=0,9175.
Найдём расчётную длину сердечника l1
¢.
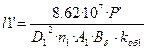 ; (1.3) ; (1.3)
 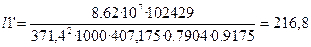 мм. мм.
Конструктивная длина сердечника статора l1
округляется до ближайшего кратного 5.
l1
= 220 мм.
Коэффициент l найдём по формуле
l= l1
/ D1
; (1.4)
l=220 / 371 = 0,593.
Из таблиц 9 – 6 и 9 – 7 находим lmax
.
Для двигателя с 2р=6 определяем lmax
= (1,46 – 0,00071 × DH
1
)∙ k4
, (1.5)
где k4
=1,05.
lmax
= (1,46 – 0,00071 · 520)∙1,05 = 1,16.
1.2 Сердечник статора.
Для данной высоты оси вращения выбираем марку стали 2312.
Сердечник собираем из отдельных отштампованных листов электротехнической стали толщиной 0,5 мм, имеющих изоляционные покрытия для уменьшения потерь в стали от вихревых токов.
Для стали 2312 используем изолирование листов лакировкой.
Коэффициент заполнения стали, принимаем равным
kС
= 0,95.
Количество пазов на полюс и фазу выбираем из таблицы 9 – 8.
При 2р = 6,
h = 280 мм,
q1
=4.
По выбранному значению q1
определяем количество пазов сердечника статора z1
в соответствии с формулой
Реклама

z1
= 2 р × m1
× q1
; (1.6)
m1
– количество фаз.
z1
= 6 × 3 ×4 = 72.
1.3 Сердечник ротора.
Для данной высоты оси вращения выбираем марку стали 2312.
Сердечник собирают из отдельных отштампованных листов электротехнической стали толщиной 0,5 мм.
Для сердечника принимаем то же изолирование листов, что и для статора – лакировкой.
Коэффициент заполнения стали принимаем равным
kc
= 0,95.
Размер воздушного зазора между статором и ротором d принимаем из таблицы 9 – 9.
При h = 280 мм и 2р = 6.
d = 0,8 мм.
Скос пазов bck=1.
Наружный диаметр сердечника ротора по формуле (9 – 5)
DН2
= D1
– 2 d; (1.7)
DН2
= 371 – 2 × 0,8 =369,4 мм.
Для высоты вращения h ³ 71 мм внутренний диаметр листов ротора рассчитываем по формуле
 D2
» 0,23 × DН1
; (1.8) D2
» 0,23 × DН1
; (1.8)
D2
» 0,23 × 520 = 119,6 мм.
Длина сердечника ротора l2
принимаем равной длине сердечника статора l1
при h =280 мм.
l2
= l1
= 220мм. (1.9)
Количество пазов на полюс и фазу находим из соотношения
q2
= q1
+ 1 (1.10)
q2
= 4 + 1 =5.
Количество пазов в сердечнике для двигателя с короткозамкнутым ротором находим по таблице 9-12 при q1
=6
z2
= 82;
2. Обмотка статора
2.1 Параметры, общие для любой обмотки
Для нашего двигателя принимаем двухслойную обмотку из провода марки ПЭТВ (класс нагревостойкости F), укладываемую в прямоугольные полуоткрытые пазы.
Обычно обмотку статора выполняют шестизонной; каждая зона равна 60 электрических градуса. При шестизонной обмотке коэффициент распределения
kР1
= 0,5/(q1
sin(α/2)), где α=60/q1
=60º/4=15º (2.1)
kР1
= 0,5/(4 × sin(7,5º)) = 0,96.
Укорочение шага принимаем равным
b1
≈ 0,8, при 2р=6.
Двухслойную обмотку выполняем с укороченным шагом по по формуле
 Уп1
= b1
× z1
/ 2p; (2.2) Уп1
= b1
× z1
/ 2p; (2.2)
Уп1
= 0,8 × 72 / 6 = 9,6.
Коэффициент укорочения определяется по формуле (9-12)
kу1
=sin(b1
∙90º) (2.3)
kу1
= sin(0,8∙90o
)=0,95.
Обмоточный коэффициент по формуле
kОБ1
= kР1
· ky1
; (2.4)
kОБ1
= 0,96 · 0,95 = 0,912.
Предварительное значение магнитного потока найдём из формулы
Ф¢ = В¢d
D1
l¢1
× 10-6
/p; (2.5)
Ф¢ = 0,7904 × 371× 220×10-6
/3= 0,02 Вб.
Предварительное количество витков в обмотке фазы
w¢1
= kн
U1
/(222 kоб1
(f1
/50) Ф¢); (2.6)
w¢1
= 0,975 × 220/(222 × 0,912 × 0,02) ≈ 53.
Количество параллельных ветвей обмотки статора а1
выбираем как один из делителей числа полюсов
а1
=3.
Предварительное количество эффективных проводников в пазу найдём по формуле
N¢п1
= w¢1
а1
/(рq1
); (2.7)
N¢п1
= 53×3/(3×4) = 13,25.
Значение Nп1
принимаем, округляя N¢п1
до ближайшего целого значения
Nп1
= 13.
Выбрав целое число, уточняем значение w1
по формуле
w1
= Nп1
рq1
/а1
; (2.8)
w1
= 13× 3 × 4/3 = 52.
Уточняем значение магнитного потока по формуле
Ф = Ф¢w¢1
/w1
; (2.9)
Ф = 0,025 × 53/52 = 0,02 Вб.
Уточняем значение индукции в воздушном зазоре по формуле
Вd
= В¢d
w¢1
/w1
; (2.10)
Вd
= 0,7904×53/52 = 0,81 Тл.
Предварительное значение номинального фазного тока найдём по формуле
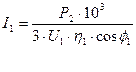 ; (2.11) ; (2.11)
 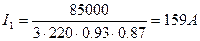 . .
Уточняем линейную нагрузку статора по формуле
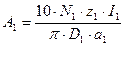 ; (2.12) ; (2.12)
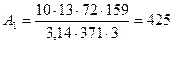 А/см.
А/см.
Среднее значение магнитной индукции в спинке статора ВС1
найдём из таблицы 9 – 13
При h = 280 мм;
2р =6;
ВС1
= 1,5Тл.
Зубцовое деление по внутреннему диаметру статора найдём по формуле
t1
= pD1
/z1
; (2.13)
t1
= 3,14×280 /72 = 16,2 мм.
2.2 Обмотка статора с трапецеидальными полузакрытыми пазами.
Принимаем предварительное значение магнитной индукции в наиболее узком месте зубца статора по таблице 9 – 14
В'з1
max
= 1,7 Тл.
Из §9.4 принимаем следующие значения:
Высота шлица hш1
=1 мм.
Высота клина hк
=3 мм.
В соответствии с этими значениями зубцовое деление статора в наиболее узком месте t1
min
определяем по формуле
t1min
=π(D1
+2 hш
1
+2 hк
)/z1
; (2.14)
t1
min
=3,14∙(371+2∙1+2∙3,5)/72=16,5 мм.
Предварительная ширина зубца статора наиболее узком месте по формуле
b'з1
min
=tmin
Вd
/kc
В'з1
max
; (2.15)
b'з1
min
=14,2∙0.81/0,75∙1,7=9,02 мм.
Предварительная ширина полуоткрытого паза в штампе по формуле
b'п1
= t1
min
– bз1
min
; (2.16)
b'п1
=16,5–9,02=7,58 мм.
Ширина шлица полуоткрытого паза
bш1
≈0,6 b'п1
; (2.17)
bш1
≈0,6∙7,58=4,5 мм.
Количество эффективных проводников по ширине паза примем из § 9-4.
Так как Nп1
= 13 то Nш
=1.
Так как h=280 то общая толщина изоляции по высоте и ширине паза соответственно равны:
2bи1
=2,2 мм.
hи1
=4,5 мм.
Допустимая ширина эффективного проводника с витковой изоляцией по
b'эф
= (b'п1
–2bи
–bc
)/Nш
; (2.18)
b'эф
=(7,58–2,2–0,3)/1=5,08 мм.
Количество эффективных проводников по высоте паза определим по формуле
Nв
=Nп1
/Nш1
; (2.19)
Nв
=13/1=13.
Предварительную высоту спинки статора найдём по формуле
h'c1
=Ф∙106
∕(2∙kc
∙l1
∙Вc1
); (2.20)
h' c1
=0,02∙106
∕ (2∙0,95∙220∙1,5)=31,8 мм.
Предварительная высота паза статора определяется по формуле
h' п1
= [ (D H1
– D1
)∕ 2]– h' c1
; (2.21)
h' п1
=[(520–371,4)/2]–31,8=42,5 мм.
Допустимая высота эффективного проводника с витковой изоляцией определяется по формуле
 h'эф
=(hп1
–hи1
–hш1
–hс
)/ Nв
; (2.22) h'эф
=(hп1
–hи1
–hш1
–hс
)/ Nв
; (2.22)
h'эф
=(42,5–4,5–3–1–0,3)/3=2,5 мм.
Площадь эффективного проводника
S'эф
= h'эф
·b'эф
;
S'эф
=2,5·5,08=12,7 мм2
.
Количество элементарных проводников в пазу конструктивно принимаем
с=2.
Количество элементарных проводников в одном эффективном по ширине вычисляется по формуле сb
= b'эф
/bдоп
с округлением до ближайшего целого значения
сb
=5,08/4,7=1.
Количество элементарных проводников по высоте паза вычисляется по формуле
са
=с/ сb
; (2.23)
са
=2/1=2.
Меньший и больший размеры неизолированного провода вычисляются по формулам
а'=(аэф
/са
)–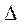 и
, где и
, где 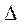 и
–двухсторонняя толщина изоляции провода. Определяем из приложения 3, аэф
–высота эффективного провода. Из § 9-4 принимаем 2,5 мм и
–двухсторонняя толщина изоляции провода. Определяем из приложения 3, аэф
–высота эффективного провода. Из § 9-4 принимаем 2,5 мм
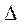 и
=0,15 мм. и
=0,15 мм.
а'=(2,5/2)–0,15=1,1 мм.
b'=(bэф
/cb
)– 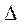 и
; b'=(5,08/1)–0,15=4,93 мм. и
; b'=(5,08/1)–0,15=4,93 мм.
Размеры провода по стандарту выбираем из приложения 2
а b=1,06 b=1,06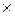 5 мм. 5 мм.
S=5,085 мм2
.
Размер по высоте паза в штампе определим по формуле
hп1
= Nв
∙ca
(a+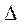 и
); (2.24) и
); (2.24)
hп1
=13∙2∙(1,06+0,15)+4,5+0,3=36,26 мм.
Размер по ширине паза в штампе определим по формуле
bп1
=Nш
∙сb
∙(b+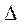 и
)+2bи
+bc
; (2.25) и
)+2bи
+bc
; (2.25)
bп1
=1∙1∙(5+0,15)+2,2+0,3=7,65 мм.
Высота спинки статора определяется по формуле
hc
1
=[(DH
1
–D1
)/2]–hп1
; (2.25)
hc
1
=[(520–371,4)/2]–36,26=38,04 мм.
Уточнённая ширина зуба в наиболее узкой части определяется по формуле
bз
1min
= t1min
– bп
1
; (2.26)
bз
1min
=16,6–7,65=8,95 мм.
Уточнённую магнитную индукцию в наиболее узкой части зубца статора определим по формуле
Вз1
max
= t1
∙Bδ
/ bз1
min
∙kc
; (2.27)
В'з1
max
=16,2∙0,75/8,95∙0,75=1,81 Тл.
Плотность тока в обмотке статора по формуле
J1
= I1
/(c·S·a1
); (2.28)
J1
= 159/(2×5,085·3 ) = 5,2 А/мм2
.
Найдём идеальную тепловую нагрузку от потерь в обмотке А1
J1
А1
J1
= 425·5,2 = 2210 А2
/(см × мм2
).
По рисунку 9 – 8 для DН1
= 520 мм получаем допустимую тепловую нагрузку
А1
J1
= 2150 А2
/(см × мм2
).
Среднее зубцовое деление статора найдём по формуле
tср1
= p(D1
+ hП1
)/z1
; (2.29)
tср1
= 3,14(371,4 + 36,26)/72 = 17,7 мм.
Средняя ширина катушки обмотки статора найдём по формуле
bср1
= tср1
уп1
; (2.30)
bср1
= 17,7 × 9,6 = 168,96 мм.
Средняя длина лобовой части обмотки по (9 – 42)
 lл1
= (1,16 + 0,14p)·bср1
+ 15; (2.31) lл1
= (1,16 + 0,14p)·bср1
+ 15; (2.31)
lл1
=(1,16+0,14×3) × 168,96+15= 282 мм.
Средняя длина витка обмотки по формуле
lcp
1
= 2 · (l1
+ lл1
) = 2 · (220 + 282) = 1004 мм. (2.32)
Длина вылета лобовой части обмотки по формуле
lв1
= 0,4 bcp
1
+hп1
/2 + 25; (2.33)
lв1
=0,4·168,96+32/2+25 = 108,584 мм.
3. Обмотка короткозамкнутого ротора
Применим обмотку ротора с бутылочными закрытыми пазами, т.к.
h = 280 мм.
Высота паза из рис. 9-12 [1] равна hп2
= 39 мм.
Расчетная высота спинки ротора при 2р=6 и h = 280 мм, по (9 – 66)
hc
2
= 0,38 · DH
2
– hп2
– 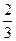 dk
2
; (3.1) dk
2
; (3.1)
hc
2
= 0,38 · 369,4 – 39 – 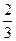 ·0 = 101,4 мм. ·0 = 101,4 мм.
Магнитная индукция в спинке ротора по формуле
Вс2
= Ф · 106
/ (2 · kc
· l2
· hc
2
); (3.2)
Вс2
= 0.022 · 106
/ (2 · 0.95 · 220 ·101,1) = 0,47 Тл.
Зубовое деление по наружному диаметру ротора по формуле
 t2
= πDн
2
/z2
; (3.3) t2
= πDн
2
/z2
; (3.3)
t2
=3,14· 369,4/82 = 14,4 мм ;
Магнитная индукция в зубцах ротора по таблице 9-18
Вз2
= 1,8 Тл ;
Ширина зубца по формуле
bз2
= t2
· Bδ
/ (Bз2
· kc
); (3.4)
bз2
= 14,14 · 0,81 / 1,8 · 0,95 = 10.73 мм.
Меньший радиус паза по формуле
; (3.5)
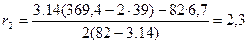 мм. мм.
Больший радиус паза по формуле
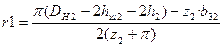 ; (3.6) ; (3.6)
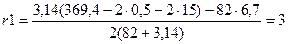 мм. мм.
Расстояние между центрами радиусов по формуле
h1
= hп
2
– h2
– hш
2
– r1
– r2
; (3.7)
h1
= 39 – 0,5 – 15 – 2,3 – 3 = 18,2 мм.
Ширина верхней части стержня по формуле
b≈(1÷1,25)∙ r1
b=1,2∙3=3,6 мм
80. Проверка правильности определения 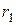 и и 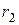 исходя из условия b32
=const.; исходя из условия b32
=const.;
π h1
–z2
(r1
– r2
)≈0
3,14·18,2 – 82(3 – 2,3) = –0,252.
Площадь поперечного сечения нижней части стержня определяется по формуле
; (3.8)
Sст.н.
=(3,14/2)(32
+2,32
)+(3+2,3)18,2=118,9 мм2
.
Размеры короткозамыкающего кольца
Поперечное сечение кольца литой клетки определяется по формуле
Sкл
= (0,35 ÷ 0,45) · z2
· Sст
/2p; (3.9)
Sкл
= 0,4 ·82 · 171,5/6 = 937,5 мм2
.
Высота кольца литой клетки определяется по формуле
hкл
= 1,1 · hп2
= 1,1 · 39 = 42,9 мм. (3.10)
Длина кольца по формуле
lкл
= Sкл
/hкл
; (3.11)
lкл
=937,5/42,9=21,9 мм ;
Средний диаметр кольца литой клетки определяется по формуле
Dкл.ср.
= DH
2
– hкл
; (3.12)
Dкл.ср
=369,4– 42,9 = 326,5 мм;
4. Расчёт магнитной цепи.
4.1 МДС для воздушного зазора.
Коэффициент, учитывающий увеличение магнитного сопротивления воздушного зазора вследствие зубчатого строения статора kd1
найдём по формуле (9 – 116)
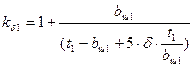 (4.1) (4.1)
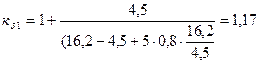
Коэффициент, учитывающий увеличение магнитного сопротивления воздушного зазора вследствие зубчатого строения ротора kd2
найдём по формуле
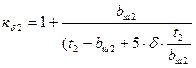 (4.2)
(4.2)
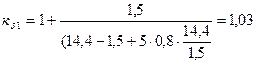
Коэффициент, учитывающий уменьшение магнитного сопротивления воздушного зазора так как радиальные каналы отсутствуют то принимаем
kк
= 1;
Общий коэффициент воздушного зазора kd
найдём по формуле
kd
= kd1
× kd2
× kк
; (4.3)
kd
= 1,17× 1,03 × 1 = 1,21;
МДС для воздушного зазора Fd
найдём по формуле
Fd
= 0,8dkd
Вd
× 103
; (4.4)
Fd
= 0,8 × 0,8 × 0,81 × 1,21 × 103
= 627,3 А.
 4.2 МДС при прямоугольных полуоткрытых пазах статора.
4.2 МДС при прямоугольных полуоткрытых пазах статора.
Зубцовое деление на 1/3 высоты зуба определим по формуле
t1(1/3)
=π∙(D1
+2hп1
/3); (4.5)
 t1(1/3)
=3,14(371,4+2∙32/3). t1(1/3)
=3,14(371,4+2∙32/3).
Ширина зуба на 1/3 высоты определяется по формуле
bз1(1/3)
= t1(1/3)
–bп1
; (4.6)
bз1(1/3)
=17,13–7,65=9,48 мм.
Магнитная индукция на 1/3 высоты зуба определяется по формуле
Bз1(1/3)
=t1
∙Bδ1
/ bз1(1/3)
∙kc
; (4.7)
Bз1(1/3)
=16,2∙0,81/9,48∙0,95=1,46 Тл .
Так как Bз1(1/3)
=1,46 то напряженность магнитного поля Hз1
(А/см) определим из приложения 9;
Hз1
=10,2 А/см; .
Среднюю длину пути магнитного потока определим по
Lз1
= hп1
; (4.8)
Lз1
= 32 мм.
МДС для зубцов найдём по
Fз1
= 0,1∙Hз1
∙Lз1
; (4.9)
Fз1
= 0,1 × 10,2× 32 = 32‚64
4.2
МДС при бутылочных пазах ротора.
Средняя ширина верхней части зубца определяется по формуле
bзв2
=π∙(Dн2
–2h2
–h)/z2
–b; (4.10)
bзв2
=3,14∙(396,4–2∙0,5–15)/82–3,6=14,2 мм.
Магнитную индукцию в среднем сечении верхней части зубца определим по формуле
Bз.в2
=t2
∙Bδ
/ bзв2
∙ kc
; (4.11)
Bз.в2
=14,4∙0,8/14,2∙0,95=0,84 Tл.
Так как Bз.в2
=0‚84 (Тл)‚то напряженность магнитного поля Hз.в2
(А/см) определим из приложения 9;
Hз.в2
=3‚11 А/см;
Средняя длина пути магнитного потока в верхней части зуба определяется по формуле
Lз.в2
=h2
+h; (4.12)
Lз.в2
=0‚5+15=15‚5 мм;
МДС для верхней части зубца ротора определяется по формуле
Fз.в2
= 0,1·Hз.в2
·Lз.в2
; (4.13)
Fз.в2
=0,1·15.5·3‚11=4‚82 A;
Магнитную индукцию в нижней части зубца определим по формуле
Bз.н2
= t2
∙Bδ
/ bзн2
∙ kc
; (4.14)
Bз.н2
=14,4∙0,8/6‚7∙0,95=1‚78 Tл.
Напряжённость поля в нижней части зубца определим из приложения 9
Hз.н2
=25 А/см;
Средняя длина пути магнитного потока в нижней части зуба определяется по формуле
Lз.в2
=r1
+h1
+0,8r2
; (4.15)
Lз.в2
=3+18,5+0,8∙2,3=23,04 мм.
МДС для верхней части зубца ротора определяется по формуле
Fз.н2
=0‚1∙ Hз.н2
∙ Lз.н2
; (4.16)
Fз.н2
=0‚1∙25∙23‚04=57‚6 А.
МДС для зубцов ротора определим по формуле
Fз.2
= Fз.в2
+ Fз.н2
; (4.17)
Fз2
=4‚48+57‚6=62‚42 А.
 4.3 МДС для спинки статора.
4.3 МДС для спинки статора.
Напряжённость магнитного поля Нс1
при Вс1
= 1.5 находим по приложению 12
Нc1
= 11,2 А/см.
Среднюю длину пути магнитного потока Lс1
найдём по
Lc
1
= p(DН1
– hc
1
)/4р; (4.18)
Lc
1
= 3,14· (520 – 42,3)/6 =125 мм.
МДС для спинки статора Fс1
определим по формуле
Fc
1
= 0,1 Нc1
Lc
1
; (4.19)
Fc
1
= 0,1 × 11‚2 ×125 = 140 А;
4.4 МДС для спинки ротора.
Напряжённость магнитного поля НС2
при 2р = 6 найдем из приложения 6
Для стали 2312 при Вс2
= 0‚47 Тл
Нс2
= 0‚74 А/см.
Среднюю длину пути магнитного потока Lс2
при 2р = 6 найдём по формуле
Lс2
= π(D2
+hс2
+ 4¤3dк2
)/4p; (4.20)
Lс2
=3,14(120+101,4+0)/12 = 57,93 мм.
МДС для спинки ротора найдём по
Fс
2
= 0,1 Нс
2
Lс
2
; (4.21)
Fс2
= 0,1 × 0.74× 57,93 = 4,29 А.
4.5 Параметры магнитной цепи
Суммарную МДС магнитной цепи на один из полюсов найдём по
Få
= Fd
+ F31
+ F32
+ FC
1
+ FC
2
; (4.22)
Få
= 672‚3 + 32‚64 + 62‚44 + 140 + 4‚29 = 866‚65 А.
Коэффициент насыщения магнитной цепи kнас
найдём по
kнас
= Få
/ Fd
; (4.23)
kнас
= 866‚65/627‚3 = 1.38;
Намагничивающий ток IM
найдём по формуле
Iм
= 2,22 Få
× р/(m1
w1
kоб1
); (4.24)
Iм
= 2,22 × 866‚65 × 3/3 × 52 × 0,912) = 40‚57 А.
 Намагничивающий ток в относительных единицах Iм
*
по формуле Намагничивающий ток в относительных единицах Iм
*
по формуле
Iм
*
= Iм
/I1
; (4.25)
Iм
*
=40‚57/159 = 0,26 о.е.;
ЭДС холостого хода Е найдём по (9 – 175)
Е = kН
∙U1; (4.26)
Е = 0,975 × 220 = 214,5 В.
Главное индуктивное сопротивление xM
найдём по
xм
= Е/Iм
; (4.27)
xм
= 214‚5/40‚57 = 5‚29 Ом.
Главное индуктивное сопротивление в относительных единицах xм
*
найдём по
xм
*
= xм
I1
¤U1
; (4.28)
xм
*
= 5‚29× 159/220 = 3‚
82 о.е.
 5. Активные и индуктивные сопротивления обмоток
5. Активные и индуктивные сопротивления обмоток
5.1 Сопротивление обмотки статора
Активное сопротивление обмотки фазы r1
при 20°С найдём по формуле
r1
= w1
∙lср1
/(rм
20
∙а1
с∙S∙103
); (5.1)
r1
= 52 × 1004/(57 ×3× 2×5‚085× 103
) = 0,03 Ом.
Активное сопротивление обмотки фазы r1
*
при 20°С в относительных единицах найдём по формуле
r1
*
= r1
I1
¤U1
; (5.2)
r1
*
= 0,03 ×159/220 = 0,0217о.е.
Проверка правильности определения r1
*
по формуле
; (5.3)
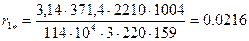
Размеры паза статора определим из § 9-4 и таблицы
bп1
=7,58 мм ; bш1
=4‚5 мм ; h3
=1мм ;
hп1
=32 мм ; hк1
=3 мм ;
h2
=1,9 мм ; hш3
=1 мм ; h1
= hп1
– hш1
– hк1
– h2
– h3
=32–1–3–1,9–1=25,1 мм.
Коэффициенты, учитывающие укорочение kb1
и k¢b1
при b1
= 0,65÷1 найдём
kb1
= 0,4 + 0,6b1
; (5.4)
kb1
= 0,4+ 0,6 × 0,8 = 0,88.
k¢b1
= 0,2+0,8 b1
; (5.5)
k¢b1
= 0,2+0,6∙0,8=0,68
Коэффициент проводимости рассеяния для прямоугольного полуоткрытого паза lп1
найдём по формуле
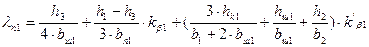 (5.6) (5.6)
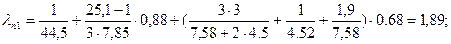
Коэффициент дифференциального рассеяния статора kд1
берем из таблицы 9 – 23, при q1
= 4 и двухслойной укороченной обмотке
kд1
= 0‚0062.
Коэффициент, учитывающий влияние открытия пазов статора на проводимость дифференциального рассеяния определим по формуле
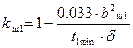 ; (5.7) ; (5.7)
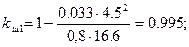
Коэффициент kр1
берем из таблицы (9 – 22) при q1
= 4, Z2
= 82 и р =3
kр1
= 0,782
Коэффициент проводимости дифференциального рассеяния lд1
найдём по
lд1
= 0,9·t1
min
(kОБ1
)2
kР1
kШ1
kД1
/(dkd
); (5.8)
lд1
= 0,9· (16,6 × 0.912)2
× 0.782 × 0.995 × 0.0062/(0,8 × 1.21) =1,03;
Полюсное деление t найдём по формуле
t1
= pD1
¤2р; (5.9)
t1
= 3.14 ×371‚4 /6 = 194,37 мм ;
Коэффициент проводимости рассеяния лобовых частей обмотки lл1
найдём по
lл1
= 0,34(q1
¤ l1
)(lЛ1
– 0,64b1
t1
); (5.10)
lл1
= 0,34 × (4/220)(282 – 0,64 · 0,8 ·194,37) = 1,19.
Коэффициент проводимости рассеяния обмотки статора l1
найдём по формуле
l1
= lп1
+ lд1
+ lл1
; (5.11)
 l1
= 1,89 + 1,03 + 1,19 = 4,11. l1
= 1,89 + 1,03 + 1,19 = 4,11.
Индуктивное сопротивление обмотки фазы статора x1
найдём по формуле
x1
= 1,58f1
l1
w2
1
l1
¤(pq1
× 108
); (5.12)
x1
= 1,58 × 50 × 220 × 522
× 4,11/(3 × 4 × 108
) = 0,16 Ом.
 Индуктивное сопротивление обмотки фазы статора x1
*
в относительных единицах найдём по формуле Индуктивное сопротивление обмотки фазы статора x1
*
в относительных единицах найдём по формуле
x1
*
= x1
I1
¤ U1
; (5.13)
x1
*
= 0,16 × 159 / 220 = 0,12 о.е.
Проверку правильности определения x1
*
в относительных единицах произведём по формуле
x1
*
= 0,39(D1
A1
)2
l1
l1
×10-7
¤(m1
U1
I1
z1
); (5.14)
x1
*
= 0,39(371,4 × 425)2
220 × 4,34 ×10-7
/(3 × 220 × 159 × 72) = 0,123 о.е.
5.2 Сопротивление обмотки короткозамкнутого ротора
Активное сопротивление верхней части стержня rст.в
при 20°С найдём по формуле
rст.в
= l2
/(rа
20
∙Sст.в
× 103
) , где (5.15)
rа20
—удельная электрическая проводимость алюминия при 20°С
rc
т.в
= 220/(27 × 52,6× 103
) = 0,000155 Ом.
Коэффициент приведения тока кольца к току стержня kпр2
найдём по формуле
kпр2
= 2π∙р/z2
; (5.16)
kпр2
= 2 × 3,14∙6/82 = 2,594.
Сопротивление короткозамыкающих колец приведённое к току стержня при 20°С
rкл
=2π∙Dкл.ср
/rа20
∙z2
Sкл
∙103
; (5.17)
rкл
=2∙3,14∙236,5/27∙82∙937,5∙0,232
∙103
Ом.
Активное сопротивление верхней части стержня приведённое к статору при 20ºС
r'ст.в
= kпр1
∙rст.в
, где (5.18)
kпр1
–коэффициент приведения сопротивления обмотки ротора к обмотке статора определим по формуле
kпр1
=(4m1
/z2
)∙(w1
∙kоб1
/kск
); (5.19)
kпр1
=(4∙3/82)∙(52∙0,912/1)=329,13.
пазы выполнены без скоса kск
=1
r'ст.в
=329,13∙1,55∙10-4
=0,051 Ом.
Активное сопротивление нижней части стержня rст.в
при 20°С найдём по формуле
rст.н
= l2
/(rа
20
∙Sст.н
× 103
); (5.20)
rст.н
=220/27∙118,9∙103
=6,85∙10-5
Ом;
Активное сопротивление нижней части стержня приведённое к статору при 20ºС найдём по формуле
r'ст.н
= kпр1
∙rст.н
; (5.21)
r'ст.н
= 329,13∙63,85∙10-5
Ом.
Активное сопротивление коротко замыкающих колец приведённое к статору при 20ºС найдём по формуле
r'o
=kпр1
∙rкл
; (5.22)
r'o
=329,13∙1,85∙10-5
Ом.
Активное результирующее сопротивление ротора найдём по формуле
r'2
= r'o
+ (r'ст.в
∙ r'ст.н
)/( r'ст.в
+ r'ст.н
); (5.23)
r'2
=0,0061+(0,051∙0,023)/(0,051+0,023)=0,022 Ом.
Коэффициент проводимости рассеяния нижней части клетки найдём по формуле
λ2н
={[(h1
+0,8∙r2
)/6∙r1
]∙(1–π∙r2
1
)2
+0,66–b/4∙r1
}+(h–0,18)/2∙b; (5.24)
λ2н
={[(25,1+0,8∙2,3)/6∙3]∙(1–3,14∙32
)2
+0,66–3,6/4∙3}+(15–0,18)/2∙3,6=3,13
Суммарный ток верхней и нижней частей стержня найдём по формуле
I2
=(2∙w∙kоб1
∙P2
/U1∙z2
)∙(0.2+0.8∙cosφ')∙103
/η' cosφ'; (5.25)
I2
=(2∙52∙0,912∙85/220∙82)∙(0,2+0,8∙0,87)∙103
/0,93∙0,87=494,9 А.
Коэффициент проводимости рассеяния взаимной индукции верхнего и нижнего пазов определим по формуле
 λн.в
=1,12∙h2
∙103
/ I2
+[(h+0,1∙b)/2∙b]+1,09; (5.26) λн.в
=1,12∙h2
∙103
/ I2
+[(h+0,1∙b)/2∙b]+1,09; (5.26)
λн.в
=1,12∙0,5∙103
/494,5+[(15+0,1∙3,6)/2∙3,6]+1,09=4,35
Коэффициент проводимости дифференциального рассеяния определим по формуле
λд2
=0,9∙t2
∙(z2
/6∙p)2
∙kд2
/δ∙kδ
; (5.28)
λд2
=0,9∙14,14(82/6∙3)2
∙0,004/0,8∙1,21=1,09.
Коэффициент проводимости рассеяния короткозамыкающих колец определим по формуле
λкл
=(2,9∙Dкл.ср.
/z2
∙l2
∙k2
пр2
)∙lg[2.35∙ Dкл.ср
/(hкл
+lкл
)]; (5.29)
λкл
=(2,9∙326,5/82∙220∙0,23)∙ lg[2.35∙326,5/(42,9+21,9)]=0,245
Коэффициент проводимости рассеяния обшей цепи ротора определим по формуле
λ20
= λн.в
+λд2
+λкл
; (5.30)
λ20
=4,35+1,09+0,245=5,685.
Приведённый коэффициент проводимости рассеяния нижней части клетки определим по формуле
λ'2н
= λ2н
∙l2
∙z1
k2
об
/(l1
∙z2
); (5.31)
λ'2н
=3,13∙220∙72∙0,9122
/(220∙82)=2,29.
Приведённый коэффициент проводимости рассеяния обшей цепи ротора определим по формуле
λ'20
= λ20
∙l2
∙z1
kоб
/(l1
∙z2
); (5.32)
λ'20
=5,685∙220∙72∙0,912/(220∙82)=4,55.
Индуктивное сопротивление нижней части клетки, приведённое к статору найдём по формуле
x'н
=x1
∙ λ'2н
/λ1
; (5.33)
x'н
=0,17∙2,29/4,34=0,0897 Ом.
Индуктивное сопротивление общей цепи ротора приведённое к статору найдём по формуле
x'0
=x1
∙ λ'20
/λ1
; (5.34)
 x'0
=0,17∙4,55/4,34=0,178 Ом. x'0
=0,17∙4,55/4,34=0,178 Ом.
Индуктивное результирующее сопротивление определим по формуле
x'2
= x'0
+x'н
∙[Sст.н
/( Sст.н
+ Sст.в
)2
]; (5.35)
x'2
=0,178+0,0897[118.9/(118.9+52.6)2
]=0.22 Ом.
Активное приведённое результирующее сопротивление ротора определим по формуле
r'2*
= r'2
∙I1
/U1
; (5.36)
r'2*
=0,022∙159/220=0,0159 Ом.
Индуктивное приведённое результирующее сопротивление ротора определим по формуле
x'2*
= x'2
∙I1
/U1
; (5.37)
x'2*
=0,22∙159/220=0,159
Проверку правильности определения x¢2
производим по формуле
x1
/ x¢2
» 0,7 ¸1,0; (5.38)
0,17/5,29=0,77.
Коэффициент рассеяния статора определим по формуле
τ1
= x1
/ xм
; (5.39)
τ1
=0,17/5,29=0,03.
Коэффициент сопротивления статора определим по формуле
ρ1
=r1
∙mт
/ (x1
+xм
),где mт
– из § 4-1, (5.40)
ρ1
=0,03∙1,38/(0,17+5,29)=7,58∙10-3
.
5.3 Сопротивление обмоток преобразованной схемы замещения двигателя (с вынесенным на зажимы намагничивающим контуром).
По формулам находим:
r'1
= mт
∙r1
=1,38∙0,03=0.04 Ом,
x'1
= x1
(1+ τ1
)=0,17∙(1+0,03)0,175 Ом,
r''2
= mт
∙r'2
∙(1+ τ1
)2
=1,38∙0,022∙(1+0,03)2
=0,032 Ом, (5.41)
x''2
= x'2
∙(1+ τ1
)2
=0,22∙(1+0,03)2
=0,23 Ом.
 Пересчёт магнитной цепи не требуется ,так как kнас
<1,7,а τ1
<0,05 Пересчёт магнитной цепи не требуется ,так как kнас
<1,7,а τ1
<0,05
 6. Режимы холостого хода и номинальный
6. Режимы холостого хода и номинальный
Реактивную составляющую тока статора при синхронном вращении Iср
найдём по формуле
Iс.р.
= U1
¤ (xм
(1 + t1
)(1 + r2
1
)); (6.1)
Iс.р.
= 220/(5,29(1 + 0,03)(1 + (7,58∙10-3
)2
)) = 40,37 А.
Электрические потери в обмотке статора при синхронном вращении Рс.м.1
найдём по формуле
Рс.м.1
= m1
I2
с.р.
r'1
; (6.2)
Рс.м.1
= 3 × 40,372
× 0,04= 195,57 Вт.
Расчётную массу стали зубцов статора, при прямоугольных пазах, m31
найдём по формуле
mз1
= 7,8∙z1
∙bз1
∙hп1
∙l1
∙kс
×10-6
; (6.3)
mз1
= 7,8 × 72 × 10,3 × 32× 220 × 0,95 × 10-6
= 37,6 кг.
Зубцовое деление найдём по формуле
t1
max
=π∙(D1
+2∙hп
)/z1
; (6.4)
t1
max
=3,14∙(371,4+2∙38)/72=19,5 мм.
Ширину зуба в наиболее широкой части найдём по формуле
bз1
max
= t1
max
–bп1
; (6.5)
bз1
max
=19,5–7,58=11,92 мм.
Ширину зуба в средней части найдём по формуле
bз1ср
= (bз1
max
+ bз1
min
)/2; (6.6)
bз1ср
=(8,95+11,92)/2=10,44 мм.
Магнитная индукция зубца статора в средней части найдём по формуле
Bз1ср
= t1
∙Bδ
/ bз1ср
∙kс
; (6.7)
Bз1ср
=16,2∙0,75/10,44∙0,95=1,23 Тл.
Магнитные потери в зубцах статора Р31
для стали 2312 найдём по формуле
Рз1
= 3В2
з1ср
mз1
; (6.8)
Рз1
= 3 × 1,232
× 37,6 = 170,6 Вт.
Массу стали спинки статора mС1
найдём по формуле
 mC
1
= 7,8∙p∙(DН1
– hс1
)∙hC
1
∙l1
kС
× 10-6
; (6.9) mC
1
= 7,8∙p∙(DН1
– hс1
)∙hC
1
∙l1
kС
× 10-6
; (6.9)
mC
1
= 7,8 × 3,14∙(520 – 42,3) · 42,3 × 220 × 0.95 × 10-6
= 103,4 кг.
Магнитные потери в спинке статора Рс1
для стали 2312 найдём по формуле
Рс1
= 3В2
с1
mс1
; (6.10)
Рс1
= 3 × 1.52
× 103,4 = 697,95 Вт.
Суммарные магнитные потери в сердечнике статора, включающие добавочные потери в стали РС
å
найдём по формуле
; (6.11)
РС
å
=170,6∙(1+2∙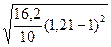 )+697,95=959,7Вт. )+697,95=959,7Вт.
Механические потери при степени защиты IP44, способе охлаждения ICO141 РМХ
å
найдём по формуле
РМХ
å
= kМХ
(n1
¤1000)2
(DH
1
/100)4
; (6.12)
Где при 2р = 6 kМХ
=1;
РМХ
å
=1( 1000/1000)2
(520/100)4
=731,1616 Вт.
Активная составляющая тока холостого хода I0а
найдём по формуле
I0а
= (РСМ1
+ РС
å
+ РМХ
å
)/(m1
∙U1
); (6.13)
I0
а
= (195,57 + 959,7 + 731,16)/(3 ×220) = 2,86 А.
Ток холостого хода I0
найдём по формуле
I0
=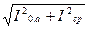 ; (6.14) ; (6.14)
I0
=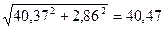 A. A.
Коэффициент мощности на холостом ходу cosj0
найдём по формуле
cosj0
= I0
a
/I0
; (6.15)
cosj0
= 2,86/40,37 = 0,069.
Активное сопротивление короткого замыкания rК
найдём по формуле
rК
= r¢1
+ r¢¢2
= 0,04 + 0,032= 0,072 Ом. (6.16)
Индуктивное сопротивление короткого замыкания xК
найдём по формуле
xК
= x¢1
+ x¢¢2
= 0,175 + 0,22 = 0,395 Ом. (6.17)
 Полное сопротивление короткого замыкания zК
найдём по формуле Полное сопротивление короткого замыкания zК
найдём по формуле
zк
=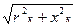 ; (6.18) ; (6.18)
zк
=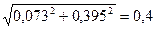 Ом. Ом.
Добавочные потери при номинальной нагрузке РД
найдём по формуле
РД
= 0,005 Р2
× 103
/h¢ = 0,005 · 85000/0,93 =457 Вт. (6.19)
Механическая мощность двигателя Р¢2
найдём по формуле
Р¢2
= Р2
× 103
+ РМХ
+ РД
= 85000 + 731+ 457 = 86188 Вт. (6.20)
Эквивалентное сопротивление схемы замещения RН
найдём по формуле
; (6.21)
Rн=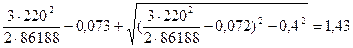 Ом. Ом.
Полное сопротивление схемы замещения zH
найдём по формуле
zн
=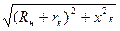 ; (6.22) ; (6.22)
zн
=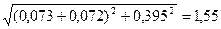 Ом. Ом.
Проверка правильности расчётов RH
и zH
RH
¤ z2
H
= Р¢2
/m1
U2
1
; (6.23)
1,43/1,552
= 85000/(3 · 2202
);
0,595 = 0,595.
Скольжение SН
найдём по формуле
SН
= 1/(1 + RH
¤ r¢¢2
); (6.24)
SН
= 1/(1 + 1,43/0,032) = 0,022 о.е.
Активная составляющая тока статора при синхронном вращении Iса
найдём по (9 – 279)
Iса
= (РСМ1
+ РС
å
)/m1
∙U1
; (6.25)
Ica
= (195,57 + 910,8)/(3 × 220) = 1,68 А.
Ток ротора I¢¢2
найдём по формуле
I¢¢2
= U1
¤ zH
= 220 / 1,55 =141,9 А. (6.26)
Ток статора, активная составляющая IA
1
найдём по формуле
 Ia
1
= Ica
+I2
''∙{[( Rн
+rк
)/zн
]+(xк
/ zн
)∙2∙ρ1
}; (6.27) Ia
1
= Ica
+I2
''∙{[( Rн
+rк
)/zн
]+(xк
/ zн
)∙2∙ρ1
}; (6.27)
Ia
1
= 1,68+141,9∙{[(1,43+0,072)/1,55]+(,395/1,55)∙2∙7,58∙10-3
}=139,7А.
Ток статора, реактивная составляющая IP
1
найдём по формуле
Iр1
= I0
+I2
''∙{(xк
/ zн
)+ [( Rн
+rк
)/zн
] ∙2∙ρ1
}; (6.28)
Iр1
= 40,47+141,9∙{(0,395/1,55)+[(1,43+0,072)/1,55]∙2∙7,58∙10-3
}=78,72 А.
Фазный ток статора I1
найдём по формуле
I1
=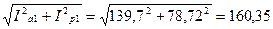 A. (6.29) A. (6.29)
Коэффициент мощности cos j найдём по формуле
cosφ= Ia
1
/ Iр1
=139,7/160,35=0,87 (6.30)
Линейную нагрузку статора А1
найдём по формуле
А1
= 10I1
Nп1
/ (а1
∙t1) = 10 · 160,35 · 13 / (3 · 16,2) = 428,9 А/см. (6.31)
Плотность тока в обмотке статора J1
найдём по формуле
J1
= I1
¤(c∙S∙a1
) = 160,35 /( 2 · 5,085 · 3) = 5,26 А/мм2
. (6.32)
Линейную нагрузку ротора А2
найдём по формуле
; (6.33)
А2
=428,9∙[141,9∙(1+0,03)∙0,912]/(160,35∙1∙1)=347,2 А/см.
Ток в стержне короткозамыкающего ротора Iст
найдём по формуле
Iст
=I'' 2
∙w1
∙kоб1
(1+τ1
)/(z2
∙kобм2
); (6.34)
Iст
=141,9∙52∙0,912(1+0,03)/82=493,9А.
Плотность тока в стержне короткозамыкающего ротора Jст
найдём по формуле
Jст
= Iст
¤SСТ
= 439,9 / 171,5 = 0,016 А / мм2
. (6.35)
Ток в коротко замыкающем кольце найдём по формуле
Iкл
= Iст
/kпр2
;
Iкл
=439,9/0,23=2147А.
Электрические потери в обмотке статора и ротора соответственно найдём по формулам
РМ
1
= m1
I2
1
r¢1
= 3 · 160,352
· 0,04 = 3085 Вт. (6.36)
PM2
= m1
I2
''2
r''2
= 3 · 141,92
· 0,032= 1933 Вт. (6.37)
Суммарные потери в электродвигателе Рå
найдём по формуле
 Рå
= РМ1
+ РМ2
+ РС
å
+ РМХ
+ РД
; (6.38) Рå
= РМ1
+ РМ2
+ РС
å
+ РМХ
+ РД
; (6.38)
Рå
= 3085+ 1933 + 697,95 + 731,1616 + 457 = 6904 Вт.
Подводимую мощность Р1
найдём по формуле
Р1
= Р2
× 103
+ Рå
= 85 · 103
+ 6904= 91904 Вт. (6.39)
Коэффициент полезного действия h найдём по формуле
h = (1 – Рå
/ Р1
) × 100 = (1 – 6904 / 91904) · 100% = 92,5 % (6.40)
Проверим Р1
по формуле
Р1
= m1
Iа1
U1
= 3 · 139,7 · 220 = 92202 Вт. (6.41)
Мощность Р2
должна соответствовать полученной по заданию
Р2
= m1
I1
U1
cos j h¤100 = 3 · 160,35 · 220 ·92,5 · 0,87 / 100 = 85167 Вт. (6.42)
 7. Круговая диаграмма и рабочие характеристики.
7. Круговая диаграмма и рабочие характеристики.
Выбираем масштаб тока cI
таким, чтобы диаметр рабочего круга диаграммы был в пределах 200 – 300 мм.
220/((200÷300)∙0,395)А/мм.
Принимаем cI
=2,5 А/мм.
Определим диаметр рабочего круга Dа
по формуле
Dа
= U1
¤(cI
∙xк
) = 220 / (2,5 · 0,395) = 223 мм. (7.1)
Определим масштаб мощности сР
по формуле
сР
= m1
U1
cI
× 10-3
= 3 · 220 · 2,5 · 10-3
= 1,65 кВт/мм. (7.2)
Iср
= 40,37/2,5 = 16,15 мм. (7.3)
Iса
= 1,68/2,5 = 0,672 мм. (7.4)
ВС = 2r1
× 100 = 2 · 7,58·10-3
· 100 =1,52 мм. (7.5)
ВЕ = r¢1
× 100¤xк
= 0,04 · 100 / 0,395 = 10,13 мм. (7.6)
BF = rк
× 100¤xк
= 0,072 · 100 / 0,395 = 18,2 мм. 7.7)
8. Максимальный момент
Переменную часть коэффициента статора lп1пер
найдём по формуле
lп1пер
= (3hк1
/(bп1
+2∙ bш1
) + hш1
/bш1
)k¢d1
; (8.1)
lп1пер
= (3 × 3/(7,58+9) + 1/4,5) × 0,97 = 0.73.
Составляющую коэффициента проводимости рассеяния статора, зависящую от насыщения найдём по формуле
l1пер
= lп1пер
+ lд
= 0.73 + 1,03 = 1,76. (8.2)
Переменную часть коэффициента ротора lп2
при бутылочных закрытых пазах найдём по формуле
λп2пер
= 1,12∙h2
∙103
/I2
; (8.3)
lп2пер
= 1,12∙1,9∙103
/494,9 =4,3.
Составляющую коэффициента проводимости рассеяния ротора, зависящую от насыщения l2ПЕР
найдём по формуле
l2пер
= lп2пер
+ lд2
= 4,3 + 1,09 = 5,39. (8.4)
Преобразованное индуктивное сопротивление общей цепи ротора, приведенное к статорному, из формулы
х''0
=x'0
(1+τ1
)2
; х¢¢н
= х¢н
(1+τ1
)2
;
х''0
=0,178(1+0,03)2
=0,189 Ом. Х¢¢н
=0,0897(1+0,03)2
=0,095 Ом.
Индуктивное сопротивление рассеяния двигателя при бутылочной форме пазов ротора, зависящее от насыщения xпер
найдём по формуле
xпер
= x¢1
l1пер
/l1
+ x¢¢0
l2пер
/l20
; (8.5)
xпер
= 0,175 × 1,76/4,3 + 0,189 × 5,39/5,685 = 0.25Ом.
Индуктивное сопротивление рассеяния двигателя, не зависящее от насыщения хпост
найдём по формуле
хпост
= х''0
(l20
– l2пер
)/l20
+ х¢¢н
∙Sст.н
/ (Sст.в
+ Sст.н
); (8.6)
хпост
= 0,175(4,34–1,76)/5,685+0,189∙118,9/(52,6+118,9)= 0,17Ом.
 Ток ротора, соответствующий максимальному моменту, при любой форме пазов статора, при открытых или полузакрытых пазах ротора I¢¢M2
найдём по формуле Ток ротора, соответствующий максимальному моменту, при любой форме пазов статора, при открытых или полузакрытых пазах ротора I¢¢M2
найдём по формуле
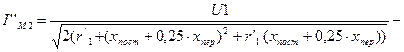
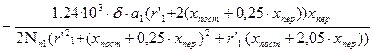 ; (8.7) ; (8.7)
I''M2
=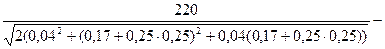
 А. А.
Полное сопротивление схемы замещения при максимальном моменте zM
найдём по формуле
zM
= U1
¤ I¢¢M2
=220 / 332,5 = 0.66Ом. (8.8)
Полное сопротивление схемы замещения при бесконечно большом скольжении z¥
найдём по формуле
z¥
=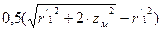 ; (8.9) ; (8.9)
z¥
=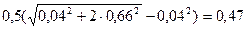 Ом. Ом.
Эквивалентное сопротивление схемы замещения при максимальном моменте RM
найдём по формуле
RM
= z¥
+ r¢1
= 0.47+ 0.04 = 0.51 Ом. (8.10)
Кратность максимального момента MMAX
¤MH
найдём по формуле
; (8.11)
MMAX
¤MH
=3∙2202
(1–0,022)/(2∙0,51∙85∙103
)=1,64 о.е.
Скольжение при максимальном моменте SM
найдём по формуле
SM
= r¢¢2
¤z¥
= 0.032/ 0.47 = 0.068 о.е. (8.12)
 Результаты расчёта рабочих характеристик двигателя.
Результаты расчёта рабочих характеристик двигателя.
| №
|
Обозначение
|
0,25Р2
|
0,5Р2
|
0,75Р2
|
Р2
|
1,25Р2
|
| |
Р2, кВт
|
21,5
|
42,5
|
63,5
|
85
|
106,25
|
| 1
|
Рд, Вт
|
115,591398
|
228,4946
|
341,3978
|
457
|
571,2366
|
| 2
|
P' 2, кВт
|
22346,5914
|
43459,49
|
64572,4
|
86188
|
107552,2
|
| 3
|
Rh, Ом
|
6,27160176
|
3,113933
|
2,020342
|
1,43
|
1,118887
|
| 4
|
zh, Ом
|
6,35588769
|
3,210326
|
2,1293
|
1,55
|
1,254686
|
| 5
|
s, о.е.
|
0,00507646
|
0,010172
|
0,015592
|
0,022
|
0,027805
|
| 6
|
I'' 2, А
|
141,935484
|
141,9355
|
141,9355
|
141,9
|
141,9355
|
| 7
|
Ia1, А
|
143,439398
|
142,7665
|
141,5161
|
139,7
|
137,0418
|
| 8
|
Iр1, А
|
51,4357195
|
60,0643
|
68,9073
|
78,72
|
87,18475
|
| 9
|
I1, А
|
152,382723
|
154,887
|
157,4008
|
160,35
|
162,4243
|
| 10
|
cos
φ
|
0,94131011
|
0,921746
|
0,899081
|
0,87
|
0,843728
|
| 11
|
Рм1, Вт
|
2786,45931
|
2878,799
|
2973,003
|
3085
|
3165,797
|
| 12
|
Рм2, Вт
|
1933,98543
|
1933,985
|
1933,985
|
1933
|
1933,985
|
| 13
|
РΣ, Вт
|
6265,14774
|
6470,39
|
6677,498
|
6904
|
7100,131
|
| 14
|
Р1, кВт
|
27765,1477
|
48970,39
|
70177,5
|
91904
|
113350,1
|
| 15
|
η, %
|
77,435208
|
86,7871
|
92,8
|
92,5
|
8
3,7361
|
 Выполнение двухслойной обмотки
Выполнение двухслойной обмотки
При 2р =6 m1
= 3, q1
= 4 z1
=72,получим
Шаг витка (ширину секции) t найдём по формуле
t = z1
/2р;
t = 72/6= 12 пазов
Укорочение шага
Y =(5/6) t=(5/6)12=10
Пазовый угол a найдём по формуле
a = р × 360°/z1
;
a = 3× 360°/72=15º
Схема статорной обмотки.
С1
® (1' – 11'') (2' – 12'') (3' – 13'') (4' – 14'') ® (26'' – 16') (25'' – 15') (24'' –14') (23'' – 13') ® (25' – 35'') (26' – 36'') (27' – 37'') (28' – 38'') ® (50'' – 40') (49'' – 39') (48'' – 38') (47'' – 37') ®(49' – 59'') (50' – 60'') (51' – 61'') (52' – 62'') ® (2''– 64') (1'' – 63') (72'' – 62') (71'' – 61') ® C4
;
С2
® (9' – 19'') (10' – 20'') (11' – 21'') (12' – 22'') ® (34'' – 24') (33'' – 23') (32'' – 22') (31'' – 21') ® (33' – 43'') (34' – 44'') (35' – 45'') (36' – 46'') ® (58'' – 48') (57'' – 47') (56'' – 46')(55'' – 45') ® (57' – 67'') (58' – 68'') (59' – 69'') (60' – 70'') ®(10'' – 72') (9'' – 71') (8'' – 70') (7'' – 69') ® С5
С3
® (17' – 27'') (18' – 28'') (19' – 29'') (20' – 30'') ® (42'' – 32') (41'' – 31') (40'' – 30') (39'' – 29') ® (41' – 51'') (42' – 52'') (43' – 53'') (44' – 54'') ® (66'' – 56') (65'' – 55') (64'' – 54') (63'' – 53') ® (65' – 3'') (66' – 4'') (67' – 5'') (68' – 6'') ® (18'' – 8') (17'' – 7') (16'' – 6') (15'' – 5') ® С6
.
 Литература.
Литература.
1. Гольдберг О. Д., Гурин Я. С., Свириденко И. С. Проектирование электрических машин. - М.: Высшая школа, 1984. – 431 с.
|