ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ РОССИЙСКОЙ ФЕДЕРАЦИИ
ЛИПЕЦКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ ЭКОНОМИКИ И ИНФОРМАТИКИ
КАФЕДРА МАТЕМЕТИЧЕСКИХ МЕТОДОВ В ЭКОНОМИКЕ
РЕФЕРАТ
НА ТЕМУ:
“ЧАСТНЫЕ ПРОИЗВОДНЫЕ”
ВЫПОЛНИЛ:
СТУДЕНТ II КУРСА ГР. И-04-2
ПИВКОВ В.А.
ПРОВЕРИЛ:
ВОРОНОВА Е.А.
г. Липецк - 2006
Содержание.
I.
Функции нескольких переменных.
II.
Частные производные
III.
Частные производные и дифференциалы высших порядков
Список литературы
ФУНКЦИИ НЕСКОЛЬКИХ ПРЕМЕННЫХ.
Определение функции нескольких переменных.
Переменная z
называется функцией двух независимых переменных x
и y
, если некоторым парам значении x
и y
по какому – либо правилу или закону ставится в соответствие определенное значение z.
Множество G
пар значений x
и y
, которые могут принимать переменные x
и y
, называется областью определения функции, а множество всех значений, принимаемых z
в области определения, - областью значений функции z
. Переменные x
и называются аргументами функции.
Пара чисел x
и y
определяет положение точки M
на плоскости xOy
с координатами x
и y
. Поэтому функцию двух переменных можно рассматривать либо как функцию двух переменных 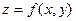 можно рассматривать как функцию точки M можно рассматривать как функцию точки M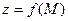 , либо как скалярную функцию векторного аргумента , либо как скалярную функцию векторного аргумента 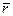 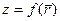 . .
Каждой тройке (x; y; z) в пространстве Oxyz соответствует точка M(x; y; z). Совершенно аналогично случаю двух переменных можно дать определение функции трех переменных 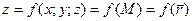 . Областью определения функции трех переменных будет все пространство или его часть. . Областью определения функции трех переменных будет все пространство или его часть.
Аналогично можно дать определение функции четырех и более переменных.
1.2
Предел функции двух переменных.
Множество точек M(x; y), координаты x и y которых удовлетворяют неравенству 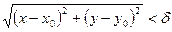 или или 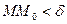 называется δ-окрестность точки называется δ-окрестность точки 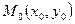 . .
Определение.
ЧислоA
называет пределом функции 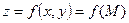 при стремлении точки M
к точке при стремлении точки M
к точке 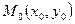 , если для любого ε>0
существует такое δ>0
, что для всех точек M
из области определения этой функции, удовлетворяющих условию , если для любого ε>0
существует такое δ>0
, что для всех точек M
из области определения этой функции, удовлетворяющих условию 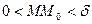 имеет место неравенство имеет место неравенство 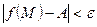 . Обозначают это так: . Обозначают это так: 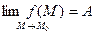 или или 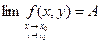
Функция  называется бесконечно малой при называется бесконечно малой при  если если 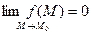
1.3
Непрерывность функции двух переменных.
Пусть точка 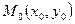 принадлежит области определения принадлежит области определения 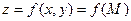 . Определение.
Функция . Определение.
Функция 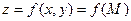 называется непрерывной в точке называется непрерывной в точке 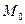 если если
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение
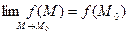 или или 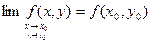 причем точка M стремится к M0
произвольным образом, оставаясь в области определения функции. причем точка M стремится к M0
произвольным образом, оставаясь в области определения функции.
Обозначим 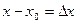 , , 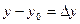 . Полным приращением . Полным приращением
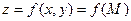 при переходе от точки при переходе от точки 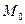 , к точке M называется разность значении функции в этой точке , к точке M называется разность значении функции в этой точке 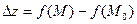 , т.е. , т.е. 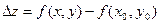
Частные производные.
2.1 Частные производные.
Частной производной
функции нескольких переменных по какой-нибудь переменной в рассматриваемой точке называется обычная производная по этой переменной, считая другие переменные фиксированными (постоянными). Например, для функции двух переменных 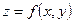 в точке в точке 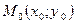 частные производные определяются так: частные производные определяются так:
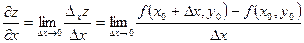 , ,
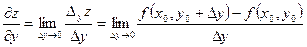 , ,
если эти пределы существуют. Величина 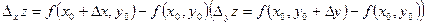 называется частным приращением
функции z
в точке называется частным приращением
функции z
в точке  по аргументу по аргументу  . Используются и другие обозначения частных производных: . Используются и другие обозначения частных производных:
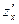 , , 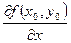 , , 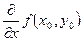 , , 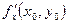 , ,
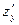 , , 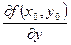 , , 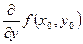 , , 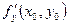 . .
Символы 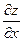 , , 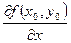 , , 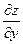 , , 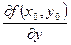 как дроби трактовать нельзя (в этом отличие от случая одной переменной). как дроби трактовать нельзя (в этом отличие от случая одной переменной).
Из определения следует геометрический смысл частной производной функции двух переменных: частная производная 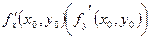 - угловой коэффициент касательной к линии пересечения поверхности - угловой коэффициент касательной к линии пересечения поверхности
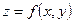 и плоскости и плоскости
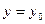 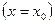 в соответствующей точке
. в соответствующей точке
.
Пользуясь понятием скорости изменения переменной, можно сказать, что частная производная 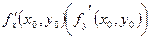 есть скорость изменения функции есть скорость изменения функции 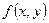 относительно относительно 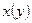 при постоянном при постоянном 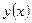 . .
Из определения частных производных следует, что правила вычисления их остаются теми же, что для функций одной переменной, и только требуется помнить, по какой переменной ищется производная.
Пример 1. Если 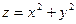 , то , то 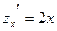 , ,  . .
Пример 2. Если 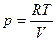 , то , то 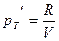 , , 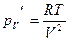 . Величина . Величина 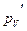 называется изотермическим коэффициентом упругости идеального газа. называется изотермическим коэффициентом упругости идеального газа.
Аналогично определяются и обозначаются частные производные функции трех и большего числа независимых переменных.
2.2
Полный дифференциал.
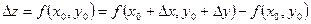 . (1) . (1)
Если приращение (1) можно представить в виде  , (2) , (2)
Где А
и В
не зависят от 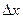 и и 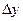 , а , а 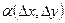 и и 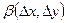 стремятся к нулю при стремлении к нулю стремятся к нулю при стремлении к нулю  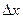 и и 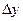 , то функция , то функция 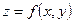 называется дифференцируемой
в точке называется дифференцируемой
в точке 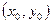 , а линейная часть , а линейная часть 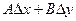 приращения функции (т.е. та часть приращения функции (т.е. та часть 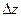 , которая зависит от , которая зависит от 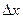 и и 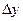 линейно) называется полным дифференциалом
(или просто дифференциалом
) этой функции в точке линейно) называется полным дифференциалом
(или просто дифференциалом
) этой функции в точке 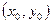 и обозначается символом и обозначается символом 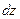 : :
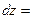 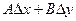 . (3) . (3)
Из определения дифференцируемости функции следует, что если данная функция дифференцируема в точке 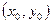 , то она в этой точке непрерывна. , то она в этой точке непрерывна.
Действительно, если в точке 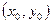 функция функция 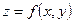 дифференцируема, то для этой точки дифференцируема, то для этой точки 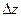 представимо в форме (2), откуда следует, что представимо в форме (2), откуда следует, что
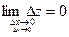 , ,
а это и означает, что в точке 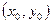 функция функция 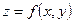 непрерывна. непрерывна.
Сервис онлайн-записи на собственном Telegram-боте
Попробуйте сервис онлайн-записи VisitTime на основе вашего собственного Telegram-бота:
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно.
Зарегистрироваться в сервисе
Из дифференцируемости функции в данной точке следует существование ее частных производных в этой точке (необходимое условие дифференцируемости
).
В самом деле, пусть функция 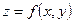 в точке в точке 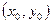 дифференцируема. Тогда имеет место соотношение (2). Полагая в нем дифференцируема. Тогда имеет место соотношение (2). Полагая в нем 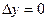 , имеем: , имеем:
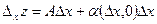 . .
Деля на 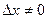 и переходя к пределу при и переходя к пределу при 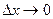 , получаем: , получаем:
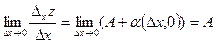 . .
Это означает, что в точке 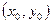 существует частная производная функции существует частная производная функции 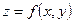 по по 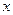 и и 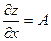 . (4) . (4)
Аналогично доказывается, что в точке 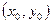 существует частная производная существует частная производная
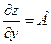 . (5) . (5)
Используя формулы (4) и (5), можно переписать выражение (3) в виде
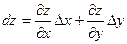 . .
Если положить 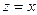 , то , то 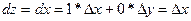 , т.е. , т.е. 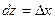 . Аналогично, полагая . Аналогично, полагая 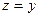 , получим , получим 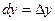 . Значит, дифференциалы независимых переменных совпадают с приращениями этих переменных, и можно записать дифференциал (3) в следующем виде: . Значит, дифференциалы независимых переменных совпадают с приращениями этих переменных, и можно записать дифференциал (3) в следующем виде: 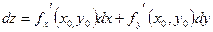 . .
Теорема
(достаточное условие дифференцируемости). Если функция 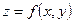 имеет частные производные в некоторой окрестности точки имеет частные производные в некоторой окрестности точки 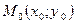 и эти производные непрерывны в самой точке и эти производные непрерывны в самой точке 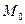 , то эта функция дифференцируема в точке , то эта функция дифференцируема в точке 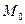 . .
Доказательство
. Дадим переменным  и и 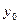 столь малые приращения столь малые приращения 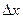 и и 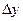 , чтобы точка , чтобы точка 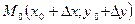 не вышла за пределы указанной окрестности точки не вышла за пределы указанной окрестности точки 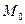 . Полное приращение . Полное приращение 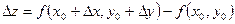 можно записать в виде можно записать в виде 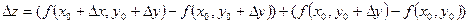 . .
Каждая из этих разностей представляет частное приращение функции. Преобразует каждую из этих разностей по формуле Лагранжа. Получим:
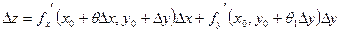 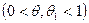 (6) (6)
Так как производные 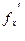 и и 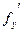 непрерывны в точке непрерывны в точке 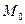 , то , то
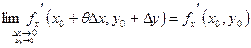 , , 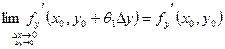
Отсюда
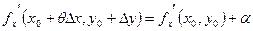 , ,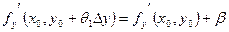 , где , где 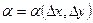 и и 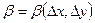 - бесконечно малые при - бесконечно малые при 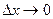 , , 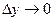 . Подставляя эти значения в равенство (6), находим: . Подставляя эти значения в равенство (6), находим:
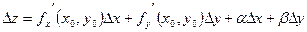 , ,
а это и означает, что функция 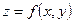 дифференцируема в точке дифференцируема в точке 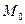 . .
2.3 Производные и дифференциал сложной функции.
Пусть 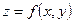 , где , где 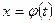 , , 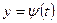 . Тогда в конечном итоге z
будет функцией одной переменной t
. Предположим, что . Тогда в конечном итоге z
будет функцией одной переменной t
. Предположим, что 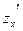 , ,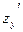 непрерывны и непрерывны и 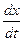 , ,  существуют. Найдем существуют. Найдем 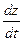 . Дадим переменной t
приращение . Дадим переменной t
приращение 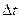 . Тогда x
,
y
,
а следовательно, и z
получат свои приращения . Тогда x
,
y
,
а следовательно, и z
получат свои приращения 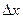 , ,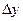 и и 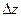 . В силу достаточного условия дифференцируемости . В силу достаточного условия дифференцируемости
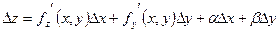 , ,
откуда
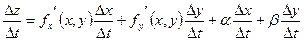 . .
Устремим теперь 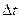 к нулю. Тогда к нулю. Тогда 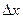 и и 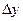 будут стремиться к нулю, так как функции x
иy
непрерывны (мы предположили существование производных будут стремиться к нулю, так как функции x
иy
непрерывны (мы предположили существование производных 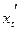 и и 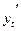 ), а потому ), а потому 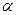 и и 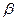 будут стремиться к нулю. В пределе получим: будут стремиться к нулю. В пределе получим:
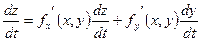 , ,
или, короче,
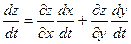 . (7) . (7)
Формула (7) называется формулой производной сложной функции
.
Пример 1. Пусть 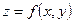 , , 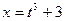 , , 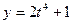 . По формуле (7) имеем: . По формуле (7) имеем:
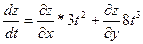 . .
Предположим, в частности, что роль независимой переменной играет, т.е. рассмотрим функцию 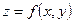 , где , где 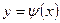 . Согласно формуле (7) будем иметь: . Согласно формуле (7) будем иметь:
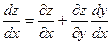 , (8) , (8)
так как 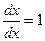 . В формуле (8) . В формуле (8) 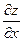 - частная производная по первому аргументу функции двух переменных - частная производная по первому аргументу функции двух переменных 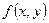 , а , а 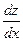 - обычная производная сложной функции одной переменной x
: - обычная производная сложной функции одной переменной x
: 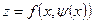 . Последнюю производную будем называть полной производной
функции. В случае, когда . Последнюю производную будем называть полной производной
функции. В случае, когда 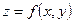 , где , где 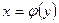 , аналогично получает: , аналогично получает:
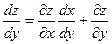
(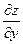 - частная производная по второму аргументу функции - частная производная по второму аргументу функции 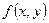 , , 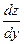 - полная производная функции одной переменной y: - полная производная функции одной переменной y: 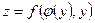 ). ).
Пусть теперь 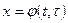 , , 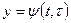 ( здесь предполагается существование первых производных функций ( здесь предполагается существование первых производных функций 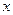 , , 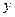 по по 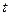 и и 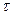 ). В этом случае z
будет функцией двух независимых переменных ). В этом случае z
будет функцией двух независимых переменных 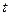 и и 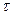 . Следовательно, для этого случая формулу (7) нужно переписать в виде . Следовательно, для этого случая формулу (7) нужно переписать в виде
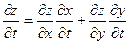 . (9) . (9)
Аналогично
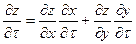 . (10) . (10)
Пример 2. Если 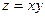 , где , где 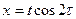 , от , от 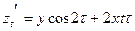 , , 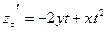 . .
Из формул (9) и (10) видно, что символ частной производной, как уже отмечалось выше, нельзя трактовать как дробь. В самом деле, если бы можно было сократить на 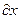 и и 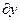 , то из формул (9) и (10) получили бы, что , то из формул (9) и (10) получили бы, что
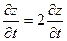 и и 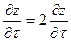 . .
2.3
Неявные функции и их дифференцирование.
Если уравнение, с помощью которого задается функция одной переменной x
, не разрешено относительно y
, то эта функция называется неявной
. Разрешая это уравнение относительно y
,
мы получаем ту же функцию, но уже заданную в явной форме. Однако часто бывает, что разрешить такое уравнение относительно y
невозможно (например, 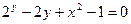 ) или нецелесообразно; в этом случае уравнение так и оставляют неразрешенным, в общем виде (когда все его члены перенесены в левую часть): ) или нецелесообразно; в этом случае уравнение так и оставляют неразрешенным, в общем виде (когда все его члены перенесены в левую часть):
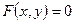 . (11) . (11)
В связи с этим встает вопрос о том, как найти производную неявной функции, не разрешая уравнения (11) относительно у
.
Если в уравнении (11), определяющем неявную функцию 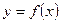 , задавать значения независимой переменной х
, то для нахождения соответствующего значения у
надо решать уравнение. Теперь, если в это уравнение подставить его решение, то получится тождество. Поэтому можно сказать также, что неявная функция , задавать значения независимой переменной х
, то для нахождения соответствующего значения у
надо решать уравнение. Теперь, если в это уравнение подставить его решение, то получится тождество. Поэтому можно сказать также, что неявная функция 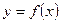 , определенная уравнением (11), - это такая функция, которая, будучи подставлена в уравнение (11), обращает его в тождество. Дифференцируя это тождество по x
согласно правилу дифференцирования сложной функции, получим: , определенная уравнением (11), - это такая функция, которая, будучи подставлена в уравнение (11), обращает его в тождество. Дифференцируя это тождество по x
согласно правилу дифференцирования сложной функции, получим:
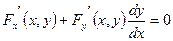 . .
Отсюда при 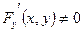 вытекает формула для производной неявной функции вытекает формула для производной неявной функции
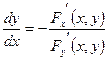 . (12) . (12)
Пример 1. Пусть y
как функция от x
задана соотношением 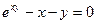 . Найти . Найти 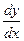 . .
Для 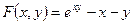 имеем: имеем: 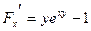 , , 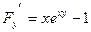 и согласно формуле (12) и согласно формуле (12)
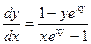 . .
Пусть уравнение 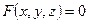 (13) (13)
Определяет z
как неявную функцию 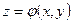 независимых переменных x
иy
. независимых переменных x
иy
.
Пользуясь формулой (12), из равенства (13) имеем:
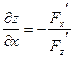 , , 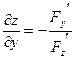 . (14) . (14)
Пример 2. Найти частные производные неявной функции z
, заданной уравнением 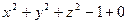 . .
Согласно формулам (14)
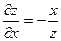 , , 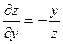
Частные производные и дифференциалы высших порядков.
3.1
Частные производные высших порядков.
Частные производные функции нескольких переменных сами являются функциями этих переменных и могут иметь частные производные. Для исходной функции эти последние производные будут частными производными второго порядка
. Так, для функции 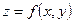 двух независимых переменных можно определить (предполагается, что все производные существуют) четыре частные производные второго порядка, которые обозначаются символами двух независимых переменных можно определить (предполагается, что все производные существуют) четыре частные производные второго порядка, которые обозначаются символами
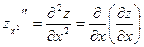 , , 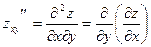 , ,
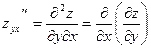 , , 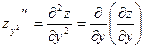 . .
Частные производные 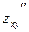 и и 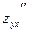 , отличающиеся порядком дифференцирования, называются смешанными частными производными второго порядка
. , отличающиеся порядком дифференцирования, называются смешанными частными производными второго порядка
.
Аналогично определяются частные производные третьего, четвертого и старших порядков.
Пример. Найти частные производные второго порядка функции 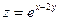 . .
Имеем:
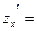 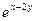 , , 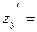 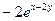 ,, ,,
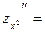 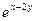 , , 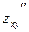 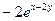 , , 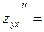 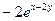 , , 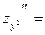 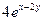 . .
Здесь 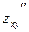 = =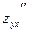 . Оказывается, имеет место следующая теорема. . Оказывается, имеет место следующая теорема.
Теорема
. Смешанные производные второго порядка равны, если они непрерывны: 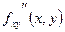 = =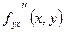 . .
Следствие.
Смешанные производные высших порядков равны, если они непрерывны и получены в результате дифференцирования по одним и тем же переменным одинаковое число раз, но может быть в разной последовательность
.
Покажем это на примере:
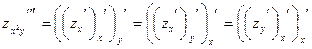 , ,
т.е.
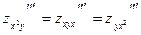 . .
Здесь мы дважды пользовались только что отмеченной теоремой: первый раз применительно к функции 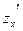 (мы изменили порядок ее дифференцирования), второй раз использовали равенство (мы изменили порядок ее дифференцирования), второй раз использовали равенство 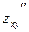 = =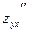 . В общем случае схема рассуждений аналогична. . В общем случае схема рассуждений аналогична.
3.2
Признак полного дифференцирования.
Выясним, при каких условиях выражение 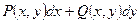 , (1) , (1)
где 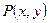 и и 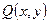 непрерывны и вместе со своими частными производными первого порядка, является полным дифференциалом некоторой функции непрерывны и вместе со своими частными производными первого порядка, является полным дифференциалом некоторой функции  , или, кратко, полным дифференциалом. , или, кратко, полным дифференциалом.
Теорема
. Выражение
(1) есть полный дифференциал тогда и только тогда, когда выполнено равенство
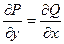 . .
3.3. Дифференциалы высших порядков.
Заметим прежде всего, что для функции нескольких переменных справедливы те же общие правила дифференцирования, что и для функции одной переменной:
I.
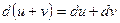 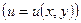 , ,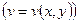 . .
II.
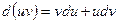 . .
III.
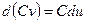 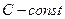 . .
IV.
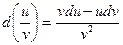 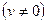 . .
Пусть имеется функция 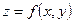 независимых переменных x
иy
, обладающая непрерывными частными производными второго порядка. Рассмотрим ее полный дифференциал независимых переменных x
иy
, обладающая непрерывными частными производными второго порядка. Рассмотрим ее полный дифференциал
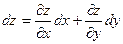
(dx
иdy
– произвольные приращения), который назовем полным дифференциалом
первого порядка
(или, кратко, первым дифференциалом
).
Так как 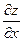 и и 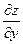 по предложению имеют непрерывные частные производные первого порядка, то от функции по предложению имеют непрерывные частные производные первого порядка, то от функции 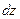 , в свою очередь, можно взять полный дифференциал , в свою очередь, можно взять полный дифференциал 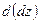 . Так получим полный дифференциал второго порядка
(или, кратко, второй дифференциал
), который обозначается . Так получим полный дифференциал второго порядка
(или, кратко, второй дифференциал
), который обозначается 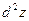 . .
Аналогично, потребовав существование непрерывных частных производных третьего, четвертого, п
-го порядков, можно получить полные дифференциалы соответственно третьего, четвертого, п
-ого порядков.
Найдем выражения для второго дифференциала через частные производные. Пользуясь правилами I, III (dx
иdy
не
зависят отx
иy
, т.е. рассматриваются как постоянные) и приведенной в п. 3.1 теоремой, можно записать:
 (2) (2)
(здесь 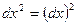 , , 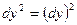 ). ).
Формула (2) обобщается на случай дифференциала п
-го порядка.
|