|   Министерство образования Российской Федерации. Министерство образования Российской Федерации.
Магнитогорский индустриальный колледж
им. Н.И. Макарова
ИССЛЕДОВАНИЕ САР РАСХОДА КИСЛОРОДА
НА ПРОДУВКУ КИСЛОРОДНОГО КОНВЕРТЕРА
Пояснительная записка
к курсовой работе по дисциплине
автоматическое управление
КР.220301.20.00.00.ПЗ
Нормоконтролер Руководитель работы
________Е.В.Менщикова __________Е.В.Менщикова
________________ _________________
Разработал студент
Группы А-03-11
__________И.Д.Творогов
2005
СОДЕРЖАНИЕ
Введение 3
1. Общая часть 4
1.1 Объект регулирования – основной элемент системы 4
1.1.1 Статические и динамические характеристики 7
1.1.2 Годограф АФХ объекта 10
1.2 Законы регулирования идеальных регуляторов 12
1.3 Частотные критерии анализа устойчивости САР 13
1.4 Качество САР и способы его улучшения 14
2. Специальная часть 19
2.1 Выбор закона регулирования. Расчёт оптимальных настроек
регулятора 19
2.2 Расчёт устойчивости САР 22
2.3 Обоснование выбора типа промышленного регулятора 25
2.4 Структурные схемы промышленных регуляторов 27
 2.5 Описание работы исследуемой САР по ее математической модели 28 2.5 Описание работы исследуемой САР по ее математической модели 28
Список используемых источников 32
Приложение А. Задание к курсовой работе
ВВЕДЕНИЕ
 Для выплавки стали существует много разных печей – мартен, электродуговые печи и т.д. Но самым рациональным способом выплавки стали на данный момент является конвертер. Для выплавки стали существует много разных печей – мартен, электродуговые печи и т.д. Но самым рациональным способом выплавки стали на данный момент является конвертер.
Для обеспечения выплавки стали нужной марки и нужного качества используется система продувки конвертера кислородом. Расход кислорода в этой системе необходимо регулировать, т.к. это влияет на результат, полученный в конце процесса. Для регулирования используются Сапфиры и контроллеры типа Simatic.
Данный проект исследует САР продувки кислородом и дает возможность рационально построить систему. Следствием этого является качественное обеспечение процесса выплавки, а значит и получение качественной продукции.
При исследовании САР выбирается закон регулирования, тип промышленного регулятора, рассчитывается система на устойчивость, рассматривается качество САР и способы его улучшения.
 Расчет привода цепного трансформатора. Расчет привода цепного трансформатора.
Исходные данные:
F = 4 кН – усиление на звездочке;
V = 0,75 м/с – линейная скорость транспортера;
P = 100 мм – шаг цепи;
z = 6 – число зубьев звездочек
Реклама

Рисунок 1. Кинематическая схема.
1. Выбор электродвигателя и кинематический расчет
1.1 Общий кпд привода:
η = η1
· η2
· η3
· η4
· η5
;
где η1
= 0,98 – КПД муфты;
η2
= 0,98 – КПД первой пары зубчатых колес;
η3
= 0,98 – КПД второй пары зубчатых колес;
η4
= 0,98 - КПД второй муфты;
η5
= 0,99 – КПД одной пары подшипника.
η = 0,984
· 0,994
= 0,89;
1.2 Мощность на звездочке транспортера
Pзв. = F · V = 4 · 0,75 = 3 кВт.
1.3 Требуемая мощность привода
Pтр. =
еэтого объекта. Снятие  временной характеристики объекта на практике, её часто называют кривой разгона объекта. временной характеристики объекта на практике, её часто называют кривой разгона объекта.
Статические объекты.татическими объектами называются объекты, у которых при поступлении ступенчатого воздействия регулируемая величина после окончания переходного процесса принимает новое постоянное значение. При определённом значении постоянной времени апериодического звена его временная характеристика с некоторым приближением совпадает с временной характеристикой объекта. Следовательно, с некоторым приближением объект регулирования в динамическом отношении можно идентифицировать с апериодическим звеном с передаточной функцией
Wоб(р)=Коб/(Тобр+1)
Статические объекты с апериодическим временными характеристиками на практике часто называют объектами с самовыравниванием.
Статические и динамические характеристики
Любой технологический агрегат, являющийся ОР, работает в установившемся режиме, если в нём полностью соблюдается материальный и энергетический баланс, т.е. если приток различных веществ в объекте равен их расходу из объекта, а количество поступившей энергии равно количеству энергии обданной.
Основные параметры, характеризующие условия протекания технологического процесса (давление кислорода – 1.6…2.5МПа; расход максимальный – 2000 м /мин; температура металла – 1200…1600 С) в установившемся состоянии остаются неизменными. При этом каждому значению входной величины объекта в установившемся состоянии соответствует определённое значение его выходной величины.
Зависимость выходной величины от входной величины в установившемся состоянии называется статической характеристикой объекта регулирования.
Статические характеристики могут быть как линейными с различными коэффициентами наклона, так и нелинейными. Эти характеристики дают возможность оценить степень связи между различными входными и выходными величинами объекта. Примером статической характеристики объекта регулирования является рис. 2.
Реклама

Рисунок 1 – статическая характеристика объекта регулирования.
Рисунок 2 – статическая характеристика первичного преобразователя
Рисунок 3 – статическая характеристика регулирующего органа
 Динамической характеристикой объекта регулирования называется зависимость выходной величины от входной в переходном режиме. Динамической характеристикой объекта регулирования называется зависимость выходной величины от входной в переходном режиме.
Большинство объектов регулирования обладает способностью постепенно приостанавливать отклонение выходной величины от первоначального значения и в них вновь устанавливается равновесное состояние.
Свойство объектов приходить после возмущения в новое установившееся состояние, без участия регулятора называется свойством самовыравнивания (саморегулирования) объекта. Статические объекты характеризуются коэффициентом самовыравнивания объекта, который называют, в какой степени отклонение параметра влияет на небаланс. Коэффициент самовыравнивания является безразмерной величиной. При р>0 получается статический объект сам, без регулятора приходит к некоторому установившемуся состоянию, причём тем быстрее и с меньшим статическим отклонением параметра, чем больше q. Задача регулятора в данном случае будет состоять в том, чтобы значительно ускорять переходные процессы в системе и сделать статические отклонения регулируемой величины достаточно малыми.
Поскольку скорость изменения регулируемой величины пропорциональна небалансу притока и расхода вещества в ОР, то она прямо зависит от емкости объекта, где это вещество может накапливаться. Чем больше величина емкости объекта, тем медленнее изменяется регулируемый параметр при одном и том же возмущении. Замедление регулируемого параметра во времени, определенное величиной емкости объекта, называют емкостным запаздыванием. Емкость – способность объекта накапливать кислород.
Отрезок времени между началом перемещения регулируемого органа и тем моментом, когда его действие начнёт сказываться на ОР, называется чистым запаздыванием.
Чем больше величины емкости и сопротивления ОР, тем больше время достижения регулируемой величиной нового установившегося значения. В зависимости от числа входящих в ОР емкостей различают емкостные и многоемкостные объекты. Чем больше количество емкостей и сопротивлений в составе ОР, тем более S-образный характер поет кривые динамических характеристик объектов и тем больше время установления нового значения регулируемого параметра.
Для определения динамической характеристики используется кривая разгона – кривая изменения во времени выходной величины в переходном процессе, вызванном однократным возмущением входной величины; при этом предполагается, что возмущение является мгновенным.
По кривой разгона определяются динамические характеристики ОР: запаздывания, постоянную времени и коэффициент передачи. Общее запаздывание тоб объекта, которое складывается из транспортного (чистого) запаздывания и емкостного (переходного) запаздывания. т.об – это условное время, в течение которого выходная величина изменилась бы от начального до нового установившегося значения. Коэффициент передачи коб статического объекта, представляет собой изменение выходной величины объекта при переходе из начального в новое установившееся состояние, отнесенное к единичному возмущению на входе. Единичным возмущением считают однопроцентное изменение входной величины объекта.
1.1.2 Годограф АФХ
На рисунке представлена АФХ апериодического звена при изменении w от 0 до бесконечности в виде полуокружности с центром на оси абсцисс в точке коб/2.
Процесс преобразования кривой разгона в АФХ (т.е. годограф) заключается в следующем:
 Строим комплексную ось координат с осями Jт = f(Re). На оси абсцисс от 0 откидываем величину kоб (взяли с кривой разгона). Середина данной величины Строим комплексную ось координат с осями Jт = f(Re). На оси абсцисс от 0 откидываем величину kоб (взяли с кривой разгона). Середина данной величины  (коб/2) будет являться центром полуокружности АФХ. Далее рассчитываем А, ф’, ф’’ и фоб для дальнейшего построения по следующим формулам: (коб/2) будет являться центром полуокружности АФХ. Далее рассчитываем А, ф’, ф’’ и фоб для дальнейшего построения по следующим формулам:
W=n/тоб;
Аоб=коб/√1+тоб *w;
Ф’=-arctg n;
Ф’’=-w*тоб*180/п;
Фоб=ф’+ф’’;
Рассчитанное ф’ откладываем в IV четверти оси координат от оси абсцисс и проводим вектора длинной до полученной полуокружности. Затем проводим радиус данного вектора, который соединится затем с вектором, полученным при обложении фоб, образуя при этом одну из точек годографа. Обложив таким образом все рассчитанные ф’ и фоб и получив точки, соединяем их при помощи лекала, образуя при этом плавный график, который может как бы закручиваться вокруг начала координат.
Для наглядности вводим пример расчета и построения АФХ системы расхода кислорода на продувку конвертера:
 Таблица 1 – Годограф АФХ объекта Таблица 1 – Годограф АФХ объекта
| N
|
w
|
Aоб
|
Ф’
|
Ф’’
|
Фоб
|
| 1
|
2
|
3
|
4
|
5
|
6
|
7
|
| 1
|
0
|
0
|
20
|
0
|
0
|
0
|
| 2
|
0,2
|
0,013
|
19,6
|
-11,3
|
3,35
|
-14,65
|
| 3
|
0,4
|
0,026
|
18,6
|
-21,5
|
-6,7
|
-28,5
|
| 4
|
0,6
|
0,04
|
17,14
|
-30,9
|
-10,32
|
-41,22
|
| 5
|
0,85
|
0,056
|
15,31
|
-40,1
|
-14,45
|
-54,85
|
| 6
|
1,2
|
0,08
|
12,8
|
-50,2
|
-20,64
|
-70,84
|
| 7
|
1,8
|
0,12
|
9,71
|
-60,9
|
-30,96
|
-91,86
|
| 8
|
2,8
|
0,186
|
6,75
|
-70,3
|
-47,98
|
-118,28
|
| 9
|
5,8
|
0,386
|
3,4
|
-80,2
|
-99,57
|
-179,77
|
| 10
|
6,0
|
0,4
|
3,28
|
-97,5
|
-106,18
|
-194,68
|
| 11
|
6,4
|
0,427
|
3,09
|
-113,3
|
-110,15
|
-223,45
|
| 12
|
7,0
|
0,467
|
2,83
|
-144,2
|
-120,46
|
-264,66
|
| 13
|
7,85
|
0,523
|
2,53
|
-184,6
|
-134,91
|
-319,51
|
Законы регулирования идеальных регуляторов
Для комплексного использования преимуществ законы П и И – регулирования в АС широко применяются регуляторы, формирующие пропорционально-интегральный закон регулирования.
ПИ – регуляторы оказывают воздействие на РО пропорционально отношению и интегралу от отклонения регулируемой величины.
У=крх+1/Ти каt.
Отсюда следует, что скорость перемещения чем в ПИ-регуляторе пропорциональна как скорости изменения регулируемой величины, так и самому изменению регулируемой величины.
Передаточная функция ПИ-регулятора
Wпи(р)=кр+1/Тир
Ти= время изодрома – это время, в течение которого первоначальное значение выходной величины регулятора удваивается вследствие действия одной только его интегральной части.
Если при настройке ПИ-регулятора установить очень большую величину постоянной времени Тк, то он превратится в П-регулятор. Если при настройке регулятора установить очень малые значения кр, то получим И-регулятор с коэффициентом передачи по скорости 1/Ти
Частотные критерии анализа устойчивости САР
Устойчивостью САР называется способность после снятия возмущения возвращаться в состояние равновесия. Если же в системе или возникают колебания со всё возрастающей амплитудой, или происходит монотонное увеличение отклонения регулируемой величины, то система называется неустойчивой.
Чтобы ответить на вопрос, устойчива или неустойчива система, достаточно найти корни её характеристического уравнения. В практике нашли широкое применение косвенные методы исследования систем на устойчивость с помощью критериев устойчивости. Они позволяют исследовать систему на устойчивость без решения характеристического уравнения.
Критерий устойчивости Найквиста – этот критерий позволяет судить об устойчивости системы в замкнутом состоянии по амплитудно-фазовой характеристике (АФХ) разомкнутой системы.
 АФХ замкнутой системы можно представить уравнением АФХ замкнутой системы можно представить уравнением
Ф(jw)=W(jw)/1tW(jw)
где W(jw) – АФХ разомкнутой системы.
Знаменатель этого выражения характеризует переходный процесс замкнутой системы.
Обозначим F(jw)=1+W(jw).
Следовательно, переходная характеристика замкнутой системы отличается от переходной функции разомкнутой системы на единицу. Исходя из анализа этого выражения выведены следующие условия устойчивости:
Если разомкнутая система устойчива, то для обеспечения её устойчивости в замкнутом состоянии необходимо и достаточно, чтобы АФХ разомкнутой системы не охватывала точку (-1;j0)
Замкнутая система устойчива, если годограф функции w(jw) разомкнутой системы при изменении частоты от 0 до бесконечности охватывает точку с координатами (-1;j0) k раз, где k – число корней характеристического уравнения разомкнутой системы, имеющих отрицательное значение.
 Качество САР и способы его улучшения Качество САР и способы его улучшения
Понятия устойчивости или неустойчивости системы определяет только факт наличия или отсутствия затухания переходного процесса в автоматической системе регулирования. Требования к качеству процесса регулирования в каждом отдельном случае определяются главным образом особенностями объекта регулирования.
Требования, предъявляемые к качественным показателям переходного процесса системы регулирования, можно представить в виде некоторой области, за пределы которой не должен выходить регулируемы параметр в переходном процессе, возникающем в результате единичного скачкообразного воздействия. Эта область является областью допустимых отклонений регулируемого параметра в переходном процессе.
 Система регулирования будет идеальной, если разность между требуемым и действительным значениями регулируемого параметра поддерживается равной нулю. Однако практически создать идеальную систему регулирования невозможно. Поэтому при разработке систем регулирования стремятся получить их характеристики, максимально приближающиеся к характеристикам идеальной системы регулирования. Очевидно, что чем меньше реальная система регулирования отличается от идеальной, тем выше будет качество процесса регулирования. Система регулирования будет идеальной, если разность между требуемым и действительным значениями регулируемого параметра поддерживается равной нулю. Однако практически создать идеальную систему регулирования невозможно. Поэтому при разработке систем регулирования стремятся получить их характеристики, максимально приближающиеся к характеристикам идеальной системы регулирования. Очевидно, что чем меньше реальная система регулирования отличается от идеальной, тем выше будет качество процесса регулирования.
Качество переходного процесса можно оценить как по виду кривой переходного процесса, так и по значению некоторых показателей: время переходного процесса, так и по значению некоторых показателей: время переходного процесса tр, перерегулирования Bмах и последовательность, установившаяся ошибка.
Время переходного процесса – время, в течение которого начиная с момента приложения воздействия на систему отклонения регулируемой величины от её установившегося значения меньше наперед заданного значения Е. Таким образом время регулирования определяет длительность переходного процесса. Перерегулированием В называется максимальное отклонение регулируемой величины от установившегося значения, выраженное в %:
В=hmax-h( )/h( ) * 100%
Колебательность системы характеризуется числом колебаний регулируемой величины за время регулирования.
Установившаяся ошибка – установившееся значение регулируемой величины по окончании переходного процесса зависит от астатизма системы.
Оценка качества процесса производится по АФХ: рассчитывается запас устойчивости системы по модулю и фазе.
 Запас устойчивости системы по модулю – расстояние точки пересечения годографа на отрицательной комплексной оси (Re) до точки (-1;j0) Запас устойчивости системы по модулю – расстояние точки пересечения годографа на отрицательной комплексной оси (Re) до точки (-1;j0)
Запас устойчивости системы по фазе – это угол, образованный вещественной отрицательной полуосью и лучом, проведенным из начала координат через точку пересечения АФХ с окружностью единичного радиуса, имеющий центр в начале координат.
Запас устойчивости по модулю показывает на сколько должен измениться модуль АФХ системы при её неизменных фазовых соотношениях для выхода системы на границу устойчивости.
Запас устойчивости по фазе – насколько возрастает запаздывания по фазе в системе на частоте среза при неизменном коэффициенте усиления на этой частоте, чтобы система оказалась на границе устойчивости.
Для улучшения качественных показателей САР в их состав вводят дополнительные устройства, называемые корректирующими – это звенья со специально подобранными передаточными функциями. Типы и способы включения корректирующих устройств могут быть различными в зависимости от того, какой недостаток надо исправить у системы. В зависимости от способа включения корректирующие устройства подразделяются на последовательные и параллельные.
Корректирующие устройства, включенные последовательно, преобразуют сигнал ошибки в производную или интеграл ко времени ошибки. Это включение увеличивает скорость воздействия на систему регулирования, но при этом требуется повышение мощности привода исполнительного механизма и прочности системы. В качестве последовательных характеризующих звеньев используется идеальные и реальные дифференцирующие звенья и интегрирующие звенья.
При параллельном корректировании замкнутая САР обязательно должна иметь обратную связь воздействия объекта регулирования на регулятор соответствует главной обратной связи. К параллельным корректирующим устройствам относятся устройства, включаемые параллельно главной обратной связи.
В зависимости от типа передаточной функции корректирующего звена размечают жёсткую и гибкую обратные связи.
Жёсткая связь осуществляется с помощью безинерционных и инерционных звеньев.
Отрицательная жёсткая связь уменьшает постоянную времени звеньев и увеличивает статическую ошибку системы. Положительная жёсткая обратная связь увеличивает коэффициент усиления и постоянную времени звена.
Жёсткая обратная связь действует в переходных и установившихся режимах.
Гибкая обратная связь действует только во время переходного процесса.
 Применение гибкой обратной связи позволяет изменять постоянные времени и структуру звеньев при постоянном коэффициенте усиления. Введение гибкой обратной связи уменьшает динамическую точность и быстродействие системы, но повышает статическую точность САР. Применение гибкой обратной связи позволяет изменять постоянные времени и структуру звеньев при постоянном коэффициенте усиления. Введение гибкой обратной связи уменьшает динамическую точность и быстродействие системы, но повышает статическую точность САР.
Положительная гибкая обратная связь служит для форсирования переходных процессов, а отрицательная – для их ослабления.
Для примера рассмотрим САР напряжения генератора с последовательным корректирующим устройством. В виде дифференцирующего контура показанного на рисунке, состоящего из конденсатора и двух резисторов.
Задача регулятора состоит в поддержании напряжения генератора при заданной настройке при различных возмущающих воздействиях.
Напряжение генератора сравнивается с заданным значением. Полученная ошибка U подается на вход корректирующего элемента (1-1’). Способность RC-контура заключается в том, что его выходное напряжение Uк равно сумме двух слагаемых, первое из которых равно отношению U, а второе – производной а( U)/at, т.е. Uk=k1( U+k2*a( U)/dt), где k1 и k2 – коэффициенты, определяемые значениями С, R1, R2. поэтому изменения регулирующего воздействия –  перестановка движка реостата в цепи обмотки возбуждения – определяется не только отклонением регулируемого параметра от заданного значения, но и скоростью изменения этого отклонения d( U)/dt. перестановка движка реостата в цепи обмотки возбуждения – определяется не только отклонением регулируемого параметра от заданного значения, но и скоростью изменения этого отклонения d( U)/dt.
2.  СПЕЦИАЛЬНАЯ ЧАСТЬ СПЕЦИАЛЬНАЯ ЧАСТЬ
Выбор закона регулирования. Расчёт оптимальных настроек регулятора.
Исходные данные регулятора.
А. По кривой разгона объекта регулирования определяется:
Коэффициент передачи объекта коб, (м3/ч)/(%ходаРО)
Коб=20
Постоянная времени объекта Тоб, с
Тоб=15
Время запаздывания тоб, с
тоб=4.5
Максимально возможное возмущение Ув, %хода РО
Ув,%хода РО, Ув-8%
Б. Требования к качеству регулирования:
Максимально допустимое значение отклонения Х1 доп, м3/мин
х1доп=67,2
Допустимое значение остаточного отклонения Хост.доп,м3/мин
Хост.доп=68,3
Допустимое время регулирования tр, с
tp=40
Допустимая величина перерегулирования В,%
в=0
Величина отношения запаздывания к постоянной времени т/Т
т/Т=4.5/15=0.3
Ориентировочно выбирается тип регулятора по это величине.
 Таблица 2 Таблица 2
| т/Т
|
Регулятор
|
| Меньше 0.2
|
Релейный
|
| Меньше 1.0
|
Непрервыный
|
| Больше 1.0
|
Непрерывный, импульсный
|
Выбираем непрерывный тип регулятора
1) при таком регуляторе рассчитываем величину динамического коэффициента регулирования Rg. Для статического объекта:
Хо=kоб*Ув;
Хо=20*8=160;
Х1=67.2;
Rg=Х1/Хо;
Rg=67.2/160=0.42;
Динамический коэффициент регулирования – величина, показывающая степень воздействия регулятора на ОР, т.е. отношение максимального отклонения регулируемой величины Х1 в переходном процессе к отношению Хо при этом же возмущении, но без регулятора, выбираем типовой процесс регулирования.
По графику Rg=f(т/Т) выбирают наиболее простой закон регулирования, который обеспечит необходимое значение динамического коэффициента регулирования Rg. Для статического объекта по рис 12 получим ПИ-регулятор.
2) в представленном графике (рис. 13) определяется относительное время регулирования.
tp/т=8;
По его величине надо определить абсолютное время регулирования
tp=tp/т*Тоб;
tp=8*4.5=36с.
И сравнить его с допустимым временем регулирования. Полученное время регулирования должно быть меньше допустимого:
tp<=tp.доп;
36<=40;
3) определение параметров максимальной динамической настройки регулятора – уравнение регулятора:
y=kpX+kp1 xdt=kp(x+1/Tu xdt);
Параметры настройки:
kp; % хода РО/м3ч – коэффициент передачи (параметр настройки П-части)
kp=0.6/(коб*тоб/Тоб);
кр=0.6/(20*4.5/15)=0.1;
где Ти, с – время изодрома (параметр настройки И-части регулятора)
Ти=0.6*Тоб;
Ти=0.6*15=9;
Подставив рассчитываемые данные, получим уравнение
у=0.1(х+1/9 хdt).
Расчёт устойчивости САР
Параметры объекта регулирования.
т=4.5с;
тоб-15с;
Коб=20м3/ч/%хода РО
Параметры регулятора
Кр=0.7/(коб*т/Тоб);
Кр=0.7/(20*4.5/15);
Порядок расчёта:
Расчёт частотных характеристик объекта с самовыравниванием
Wоб(jw)=kоб/(1+j*Tоб*w)*e ;
Aоб(w)=коб/ 1+Тоб2*w2;
 Фоб(w)=-(wт+arctgTоб*w); Фоб(w)=-(wт+arctgTоб*w);
Расчёт частотных характеристик для пропорционально-интегрального регулятора.
W(jw)=kp* (1/w2*Tu2+1);
Ap(w)=kp* (1/w2*Tu2+1);
Фр(w)=arctg(w*Tu)-п/2;
 Частотные характеристики разомкнутой системы рассчитываются по формулам Частотные характеристики разомкнутой системы рассчитываются по формулам
A(w)=Aоб(w)*Ap(w);
Ф(w)=Фоб(w)+Фр(w);
Частоте предают значения от 0 до бесконечности, чтобы найти значения величин: A(w), Aоб(w), Ap(w), Ф(w), Фоб(w), Фр(w)
Полученные данные заносят в таблицу:
 Таблица 3 - АФХ объекта регулирования и разомкнутой САР Таблица 3 - АФХ объекта регулирования и разомкнутой САР
| w
|
Wоб(jw)
|
Wp(jw)
|
W(jw)
|
| Aоб(w)
|
Фоб(w)
|
Ap(w)
|
Фр(w)
|
A(w)
|
Ф(w)
|
| 0
|
20
|
0
|
-
|
-90
|
-
|
-90
|
| 0.013
|
19.6
|
-14.65
|
0.8628
|
-82.23
|
16.91
|
-96.87
|
| 0.026
|
18.6
|
-28.5
|
0.4431
|
-74.73
|
8.24
|
-103.23
|
| 0.04
|
17.14
|
-41.22
|
0.3031
|
-67.22
|
5.19
|
-108.44
|
| 0.056
|
15.31
|
-54.85
|
0.2302
|
-59.54
|
3.52
|
-114.39
|
| 0.08
|
12.8
|
-70.84
|
0.1814
|
-49.97
|
2.32
|
-120.81
|
| 0.12
|
9.71
|
-91.86
|
0.1489
|
-38.44
|
1.44
|
-130.31
|
| 0.186
|
6.75
|
-118.28
|
0.1311
|
-27.11
|
0.88
|
-145.39
|
| 0.383
|
3.4
|
-179.77
|
0.1201
|
-13.86
|
0.41
|
-193.07
|
| 0.4
|
3.28
|
-194.68
|
0.1199
|
-13.39
|
0.39
|
-208.07
|
| 0.427
|
3.09
|
-223.45
|
0.1195
|
-12.57
|
0.36
|
-236.02
|
| 0.467
|
2.83
|
-264.66
|
0.1191
|
-11.53
|
0.337
|
-276.19
|
| 0.523
|
2.53
|
-319.51
|
0.1186
|
-10.32
|
0.29
|
-329.83
|
По виду годографа выявляют устойчива ли система и в случае её устойчивости находят запасы устойчивости по модулю и фазе.
Запас по модулю
C=1-a;
C=1-0.4772=0.5228;
Вывод: построенный годограф АФХ разомкнутой системы не охватывает на комплексной плоскости точку Б с координатами (-1;j0). Следовательно замкнутая система АР с выбранным ПИ-регулятором устойчива.
2.3 Обоснование выбора типа промышленного регулятора
Выбор конкретного вида регулятора определяется:
1) статическими и динамическими свойствами объекта регулирования;
2) требуемым качеством регулирования;
3) условиями согласования регулятора со смежной аппаратурой;
4) параметрами окружающей среды – температурой, влажностью, вибрацией, наличием магнитных полей, химической агрессивностью, взрывоопасностью и т.п.;
5) надёжностью;
6) условиями обслуживания и ремонта;
7) экологическими показателями;
8) номенклатурой выпускаемых приборов.
При создании новой системы автоматического регулирования желательно комплектовать её приборами агрегатных унифицированных систем, которые включают в себя отдельные типовые блоки со стандартизированными
 входными и выходными сигналами, позволяющие составлять разнообразные варианты схем регулирования. Такой подход облегчает проектирование, монтаж, наладку и эксплуатацию систем автоматики и предопределяет их экологическую эффективность. входными и выходными сигналами, позволяющие составлять разнообразные варианты схем регулирования. Такой подход облегчает проектирование, монтаж, наладку и эксплуатацию систем автоматики и предопределяет их экологическую эффективность.
При выборе приборов по виду используемой для создания управляющего воздействия энергия руководствуется анализом преимуществ и недостатков регулятора
Электрические регуляторы.
Преимущества:
a) питание от централизованных электрических сетей без специальных источников электроснабжения;
b) практически неограниченный радиус действий;
c) независимость рабочих характеристик от температуры и давления окружающей среды;
d) легкость монтажа и демонтажа;
e) значительная стандартизация и лёгкая заменяемость деталей;
Недостатки:
a) меньшая возможность плавного регулирования скоростей исполнительных механизмов;
b) пониженная надежность аппаратуры из-за наличия контактов в ряде элементов и хрупкости реле, ламп и т.д.
c) сравнительная сложность наладки и эксплуатации, требующая высокой квалификации обслуживающего персонала;
d) относительно низкий вид.
Электрические регуляторы, в состав которых входит электронно-ламповый или полупроводниковый усилитель, называются электронными. Электронные регуляторы могут осуществлять позиционное и непрерывное регулирование и формировать любой закон регулирования (П, И, ПД, ПИ и ПИД)
 Одним из условий предъявляемых к регулятору, является обеспечение требуемого качества регулирования. Независимо от конструктивного выполнения регулятора качество осуществляемого им процесса регулирования определяется законом регулирования. Одним из условий предъявляемых к регулятору, является обеспечение требуемого качества регулирования. Независимо от конструктивного выполнения регулятора качество осуществляемого им процесса регулирования определяется законом регулирования.
Основываясь на вышеизложенных условиях выбора регулятора и преимуществах электронного, мой выбор останавливается на современных разработках. Sumatic является прибором очень удобным в эксплуатации, т.к. необходимую программу работы можно в него заложить через ЭВМ.
2.4 Структурные схемы промышленных регуляторов.
В промышленных автоматических регуляторах для реализации Пи-законы регулирования используют отрицательную обратную связь.
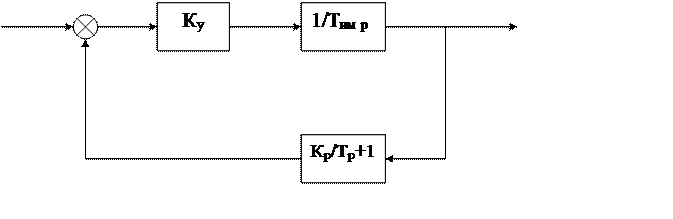
Рисунок 4– структурная схема промышленного ПИ-регулятора.
По структурной схеме формирования закона ПИ-регулирования осуществляется аналогично идеальному ПИ-регулятора. Для уменьшения отрицательного влияния на закон Пи-регулирования ИМ он имеет отрицательную обратную связь в виде усилительного звена wос(р)=кос.
Передаточная функция реального ПИ-регулятора имеет вид:
Wр(р)=(wпи(р)/кос)*(1/тбр+1);
Таким образом ПИ-регулятор реализует Пи-закон с погрешностью, определяемой балансным апериодическим звеном, постоянная времени которого
Тб=Тим/кос;
При увеличении kос Тб уменьшается и уменьшается погрешность реализации закона. Но при увеличении kос ещё уменьшается коэффициент передачи ПИ-регулятора, который равен отношению kр/kос. Для сокращения требуемого значения коэффициента передачи регулятора одновременно с увеличением kос следует пропорционально увеличивать kр.
2.5 Описание работы исследуемой САР по ее математической модели
Состояние автоматической системы регулирования, при котором возмущения отсутствуют и регулируемая величина равна заданному значению, называют равновесным.
В случае нарушения равновесия под влиянием каких-либо возмущающих воздействий наступает неустановившийся режим, который сопровождается отклонением регулируемой величины и изменением регулирующего воздействия.
Когда САР по расходу кислорода выходит из состояния равновесия, вернуть равновесие помогает регулятор, в роли которого выступает контроллер зарубежной фирмы Sumatic.
 Регулирование системы происходит не только по расходу кислорода 1а, но и по температуре 1б и давлению кислорода 1в (рис 16). Корректирующие воздействия также поступают на контроллер. Регулирование системы происходит не только по расходу кислорода 1а, но и по температуре 1б и давлению кислорода 1в (рис 16). Корректирующие воздействия также поступают на контроллер.
При поступлении возмущающего воздействия на систему (увеличение давления, допустим) изменяется расход кислорода.
Последний измеряют Сапфиром за счёт перепада давления на диафрагме унифицированный токовый сигнал с дифманометра поступает на показывающий и регистрирующий прибор Диск 1г, после чего идёт на контроллер 1д.
Конструкция Sumatic настолько сложна, что полностью его действие описать очень трудно. Но данный прибор программируется с ПК и эта программа позволяет регулировать расход кислорода.
Измеряемая величина и корректирующая воздействия, поступающие на контроллер, способствуют выработке аналогового или дискретного унифицированного сигнала, который поступает на исполнительный механизм 1е МЭО изменяет положение регулирующего клапана, а под воздействием него изменяется расход кислорода. И остается в таком положении до тех пор, пока давление кислорода в трубопроводе не придет в норму. Тогда измеряемая величина опять зафиксируется датчиком Сапфир, поступит на Диск и контроллер Sumatic. Контроллер, за счет вложенной в него программы, опять выработает сигнал, который поступает на МЭО потом, и последний изменит положение регулирующего клапана на исходное положение, т.е. до возмущения.
Структурную схему можно представить в виде ТДЗ. Поэтому на рис. 5представлена структурная схема САР расхода кислорода в виде соединения ТДЗ – математическая модель САР.
Рисунок 5 – Математическая модель САР
 Таблица3. Описание типовой структурной схемы: Таблица3. Описание типовой структурной схемы:
| Наименование
элемента ти-
повой САР
|
Наименование
элемента проектируемой
САР
|
ТДЗ
|
Передаточная функция
|
К настр-ойки
|
| 1.ЗУ
|
усил.
|
W(p)=K
|
K=
|
| 2.ПИП
|
усил.
|
W(p)=K
|
K=
|
| 3.СУ
|
Усил.
|
W(p)=K
|
K=1
|
| 4.УФЗР
|
Пи-закон
|
W(p)=Kp(1/Tиp)
|
K=
T=
|
| 5.УУ
|
Усил.
|
W(p)=K
|
K=
|
| 6.ИМ
|
Интегр.
|
W(p)=1/Tиp
|
T=
|
| 7.РО
|
Усил.
|
W(p)=K
|
K=
|
| 8.ОР
|
Апер.
Чист. зап.
|
W(p)=Kоб/1+Tобр * e
|
K=
T=
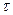 = =
|
Описание типовой структурной схемы:
1) задающее устройство – задатчик РЗД-22 (усилительное ТДЗ) – оказывает воздействие на вход системы.
2) первичный измерительный преобразователь – дифманометр Метран-100 (усилительное ТДЗ).
3) элемент сравнения – линейный электронный усилитель (усилительное ТДЗ). Коэффициент элемента сравнения Кэс=1.
4) устройство, формирующее закон регулирования – пропорционально-интегральный закон регулирования (пропорционально-интегральное ТДЗ).
5) усилительное устройство – ПБР-2М (усилительное ТДЗ).
6) исполнительный механизм – МЭО (интегрирующее ТДЗ).
7) регулирующий орган – поворотная заслонка (усилительное ТДЗ).
 8) объект регулирования – Кислородный конвертер (апериодическое, чистого запаздывания ТДЗ). 8) объект регулирования – Кислородный конвертер (апериодическое, чистого запаздывания ТДЗ).
Построим график типового апериодического процесса регулирования для САР расхода воды для 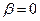 %. %.
Рисунок 6 – Апериодический процесс регулирования
Характер переходного процесса и качество регулирования для данного объекта зависит от закона регулирования и настройки регулятора.
При различных настройках одного и того же регулятора и при одних и тех же динамических свойствах объекта регулирования и возмущениях можно
получить различные переходные процессы, отличающиеся величиной перерегулирования и другими показателями качества.
Апериодический 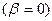 процесс имеет минимальное время регулирования, не имеет перерегулирование и выдаёт наибольшее значение Х1. процесс имеет минимальное время регулирования, не имеет перерегулирование и выдаёт наибольшее значение Х1.
Применяют в тех случаях, когда требуется минимальное время регулирования, перерегулирование не допускается, а динамическое отклонение может быть сравнительно большим.
Список используемых источников

1. К.И. Котов, М.А. Шершевер. «Средства измерения, контроля и автоматизации ТП. Вычислительная и микропроцессорная техника» - Металлургия – 1989г. Москва.
2. В.Ю. Каламов, О.М. Блинов, А.М. Бельнький. «Автоматизация управления металлургическими процессами» - Металлургия – 1974 г. Москва.
3. А.П. Конелович. «Автоматическое регулирование в черной металлургии. Краткий справочник» - Москва 1963г.
4. А.С.Клюев. «Автоматическое регулирование» - энергия – 1973г. – Москва.
5. Е.М. Гордин. К.Я. Стародуб. «Автоматическое регулирование» - Высшая школа – 1976 г. Москва.
6. А.С.Клюев «Автоматическое регулирование» - Энергия – 1976 г.Москва.
7. «Общая металлургия» под ред. П.П.Арсентьева и др. – Металлургия – 1986 г.Москва.
8. А.И. Гудзенко «Основы теории автоматического регулирования» - Высшая школа – 1976 Москва.
9. Д.И. Туркения. «Управление плавкой стали в конвертере» - Металлургия – 1971г. Москва.
10. А.С.Клюев «Автоматическое регулирование» - Высшая школа – 1986г. Москва.
11. Иванов В.А. «Математические основы теории» - энергия – 1971г. Москва.
12. Гордин Е.М. и др
13. «Основы автоматики и вычислительной техники» - машиностроение – 1978г. Москва.
|